基于代理模型的高超声速气动热模型降阶研究

2016-11-25陈鑫刘莉岳振江

北京理工大学学报 2016年4期

关键词：翼面超声速气动

陈鑫，刘莉，岳振江

(北京理工大学宇航学院，飞行器动力学与控制教育部重点实验室，北京 100081)

基于代理模型的高超声速气动热模型降阶研究

陈鑫，刘莉，岳振江

(北京理工大学宇航学院，飞行器动力学与控制教育部重点实验室，北京 100081)

高超声速飞行器气动热的快速准确预测是当前高超声速气动热弹性分析的重要前提. 针对当前高超声速气动热工程计算、高精度数值计算和实验研究均不能很好适应工程应用的问题，结合代理模型的基本思想，提出了基于代理模型的高超声速气动热模型降阶方法，建立了一种高超声速气动热模型降阶框架. 以典型高超声速三维翼面为例，对比拉丁超立方采样方法lhsdesign函数和改进的逐次枚举的拉丁超立方方法SLE，利用相同的设计样本点和代理模型构造方法，SLE方法构造的降阶模型预测翼面温度平均误差、L∞和eNRSME均小于lhsdesign方法，SLE采样方法有助于提高降阶模型的精度；对比Kriging和RBF两种代理模型构造方法，Kriging方法构造降阶模型优于RBF方法. 针对典型的高超声速三维翼面气动热预测表明，本文高超声速气动热降阶方法具有较高的精度和效率.

高超声速；气动热；代理模型；模型降阶

气动热弹性分析涉及气动、结构、控制和推进等多个系统，在高超声速飞行器的分析和优化设计过程中越来越受到重视. 高超声速飞行器气动热的快速准确预测是气动热弹性分析的重要前提. 目前，主要利用气动加热工程计算、计算流体力学(computational fluid dynamics， CFD)数值计算和实验研究3种方法来预测高超声速气动热环境. 基于简单几何假设的气动加热工程计算忽略了真实气体效应、气流黏性等，仅适用于平板或圆柱等简单飞行器构型的气动热预测[1-2]. 已有文献研究表明忽略真实气体黏性和真实气体效应甚至会直接影响到分析精度[3]. CFD数值计算能够充分考虑气流黏性、真实气体效应等，捕捉激波及边界层转捩等现象，能较好地求解耦合分析中广泛存在的非线性方程，王卫星等[4]研究指出边界层转捩对壁面热流密度分布影响较大. 由于巨大的分析自由度以及由于不确定性和设计优化需要的重复计算导致CFD计算量巨大[3]. 高超声速气动热的实验研究成本较高，同时实验研究大部分仅关注凸起等局部特性对流场边界层的影响[5]，当前应用并不广泛. 因此，开展相应地气动热降阶模型(reduced order model， ROM)研究已经成为一个较为活跃的领域.

代理模型是通过数学方法，构造出一个计算量较小，但计算结果与数值分析结果或真实物理试验结果相近的近似数学模型，以代替原数值分析模型或真实物理试验. 代理模型以其较好的近似精度和鲁棒性，近10年来被广泛应用于飞行器分析设计领域. 杨华等[6]利用径向基函数，解决了复杂形状机翼的二维气动力代理模型的构造问题. 梁煜等[7]基于计算流体力学分析结果构建Kriging气动力代理模型，用于气动布局参数匹配优化设计，提高设计效率并保证了可信度. 夏露等[8]提出了一种基于Kriging自适应代理模型的气动优化方法，成功应用于翼型气动性能优化设计.

针对高超声速气动热的模型降阶研究目前较少，本文结合代理模型基本思想，提出了一种基于代理模型的高超声速气动热的降阶模型方法，建立了高超声速气动热模型降阶框架. 典型三维翼面算例验证了降阶模型的可行性，该降阶模型有助于推动CFD技术推广到实际工程应用.

1 代理模型

代理模型的基本思想是利用原始高精度模型或试验获得一组样本点，利用代理模型构造方法从这组样本点中提取输入参数和输出参数的近似关系进而建立一个模拟原始高精度模型的模型[9]. 试验设计方法和代理模型构造方法是代理模型的两个重要组成部分.

1.1 试验设计方法

试验设计DoE(design of experiment)方法是一种科学合理的数学安排，在设计空间内获取能反映精确模型特征样本点的方法. 试验设计的目标是通过尽可能少的样本点尽可能地反映空间内精确模型的特征. 空间均匀性和投影均匀性是衡量试验设计方法的主要标准. 常用的试验设计方法有均匀试验设计、中心复合设计和拉丁超立方设计等. 本文选取常用的Matlab平台的拉丁超立方试验设计方法lhsdesign函数和基于Maxmin准则逐次局部枚举的改进拉丁超立方试验设计方法[10](successive local enumeration， SLE).

1.1.1 拉丁超立方设计方法

拉丁超立方试验设计是一种分层抽样方法，其试验设计点在设计空间内分布较均匀，且试验次数等于水平数. 拉丁超立方试验设计点的生成方法为

(1)

式中:1≤j≤n，1≤i≤m，n为因素个数或设计变量个数，m为样本点个数；U为[0，1]区间内的随机数；i为第i次试验；j为第j个设计变量；π为0，1，…，m-1的独立随机排列.

标准的拉丁超立方设计方法仅具有投影均匀性的特点，为了获得好的空间均匀性，学者开始研究最优拉丁超立方采样方法(optimal latin hypercube design， OLHD)，本文采用Matlab中lhsdesign函数优化采样方法，lhsdesign函数采样标准参数设置为“maximin”，迭代次数为100.

1.1.2 基于Maxmin准则逐次局部枚举的改进拉丁超立方设计方法(SLE)

基于Maxmin准则的逐次局部枚举拉丁超立方试验设计方法SLE的采样过程是一个简单的局部优化过程，目标为待选定的样本点与已生成的样本点之间的最小距离最大化. 与其它现有拉丁超立方采样算法最大的不同在于，其它算法采样过程中有全局目标函数，而SLE方法采样过程中的目标函数为局部的最小距离最大化.

对比研究表明SLE采样方法具有很高的采样效率和精度，均优于lhsdesign，且不受采样点个数和采样空间维数的限制，具有很好的通用性[10].

1.2 代理模型构造方法

常用的代理模型方法有多项式相应面、移动最小二乘法、径向基函数、Kriging模型、神经网络等. 本文中分别采用径向基函数(radial basis function， RBF)和Kriging模型.

1.2.1 径向基函数

径向基函数(RBF)是一类以未知点与已知数据点之间的欧式距离作为自变量的函数. 基本形式为

(2)

(3)

式中c=1/σ2，σ为高斯函数的宽度，本文取为2.0.

1.2.2Kriging函数

Kriging模型是对空间中分布的数据点进行求线性最优、无偏内插估计的一种方法. 表达式为

(4)

式中:g(X)为设计空间范围内关于X的全局近似模型;z(X)为均值为0，方差为σ2，协方差不为0的随机过程. 协方差矩阵为

(5)

(6)

引入相关向量，

(7)

Kriging模型可表示为

(8)

式中:β为未知参数；σ2和R都为θ的函数；y为由采样点响应值组成的ns维列向量.β和σ2由最小二乘估计得到

(9)

2 基于代理模型的模型降阶方法

代理模型用来建立输入参数与单输出参数或少量输出参数的近似关系，例如利用代理模型建立机翼气动外形的几何参数蒙皮厚度、翼梁厚度等与升力系数或阻力系数等气动参数的近似拟合关系. 通常仅知道简单的气动参数不能满足实际工程设计要求，如高超声速气动热弹性分析和气动热防护设计时需要得到整个翼面各处温度分布情况. 因此如何准确高效得到整个流场参数具有较大研究意义.

对于确定构型的绕流流场，描述构型流场的数量为构型表面流场网格单元数与流场变量个数的乘积. 针对高超声速飞行器气动热预测，温度为标量，描述高超声速飞行器气动热流场的个数为飞行器表面流场网格单元数.

如图1所示，利用代理模型预测气动热步骤如下.

步骤1 确定设计空间和设计变量. 针对高超声速机翼气动热预测，设计变量选为飞行马赫数、飞行高度和飞行攻角，设计空间为飞行马赫数、飞行高度和飞行攻角的上下限范围.

步骤2 运用试验设计方法获得设计空间内的样本点I(i)，i=1，2，…，n，n为样本点个数；样本点在设计空间内保证空间均匀性和空间正交性.

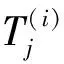
步骤4 利用代理模型方法构造设计样本点与翼面上的每一个节点温度之间的近似拟合关系. 翼面共有p个节点，即建立p个近似拟合关系.

3 高超声速气动热模型降阶框架

针对高超声速飞行器气动热计算遇到的复杂耗时的非线性数值求解难题，基于代理模型提出一种快速高效的高超声速气动热模型降阶(ROM)框架，如图2所示.

降阶模型框架主要包括:物理模型的选择；设计变量及设计空间的确定；高精度数值计算；surrogate方法构造降阶模型；降阶模型近似精度评估.

4 算例验证及分析

4.1 模型描述及设计空间的确定

本文中选取气动热结构分析中常用的典型的F104战斗机的机翼，该机翼被多次运用来做典型的高超声速分析源于其有良好的工程应用背景[11]. 机翼相关参数如图3所示.

F104机翼的气动热设计变量和设计空间如下. 马赫数：5.0≤Ma≤10.0;攻角:-8.0°≤α≤8.0°;飞行高度:20 km≤H≤40 km.

初始选取100个样本点，采用拉丁超立方试验设计方法Matlab的lhsdesign函数以及基于Maxmin准则的逐次局部枚举改进的拉丁超立方(SLE)方法分别产生.

4.2 高超声速气动热数值计算

本文高超声速气动热计算采用CFD-Fastran求解器计算F104翼面的温度分布和热流分布.

Mcnamra J J[11]指出在计算高超声速气动热建议采用B-L湍流模型，B-L湍流模型是一种最基本的湍流模型，能更好地反应高超声速流中的非线性特征. 董素君等[12]利用CFD-Fastran求解器针对典型双锥面得到不同湍流模型计算高超声速气动热流，指出B-L湍流模型计算快，能达到较好的准确性，建议气动热计算采用B-L模型，同时指出近壁面第一层网格间距y-plus需保证在1以下. 阎超等[13]通过探讨了CFD热流计算的格式效应及网格效应，研究指出AUSM格式在热流计算精确性方面具有优势. 潘沙等[14]和覃文洁等[15]指出气动热的数值模拟中，网格因素非常关键，计算结果对网格，特别是网格壁面附近的法向网格间距十分敏感，同时指出气动热计算收敛的判断比压力收敛缓慢的多，建议采用直接观察气动热数据来判断收敛.

因此，本文计算采用B-L湍流模型，空间格式采用高阶AUSM，并且严格保证近壁面网格的大小，计算时保证气动热收据的收敛性.

董素君等[12]通过典型双锥面得到不同湍流模型计算高超声速气动热流，并与试验数据对比指出了Fastran求解器计算高超声速飞行器气动热的可行性. 如图4所示，进一步通过与文献[11]中CFL3D求解器对比得到，文献[11]中CFL3D求解器翼面前缘驻点温度为938.0 K，Fastran计算驻点温度为988.3 K，翼面上温度梯度分布趋势相近，翼面温度分布情况总体相差并不大，因此本文均采用CFD-Fastran求解器计算F104翼面的温度分布和热流分布.

本文采用计算流体网格如图5所示，分别针对42.0万、81.9万和158.0万的计算域进行网格无关性验证，如表1所示，当网格计算量为42.0万时，平均y-plus为3.82，驻点温度为1 078.6 K. 随着网格计算量增大到81.9万，近壁面网格平均y-plus减小为0.76，驻点温度为988.3 K. 进一步增加网格数量，平均y-plus减小到0.45，驻点温度相比于81.9万网格并未明显减小，为987.9 K. 网格无关性验证计算结果得到，计算样本点均可采用选取81.9万网格作为计算网格.

Tab.1 Leading edge temperature with different number of grids

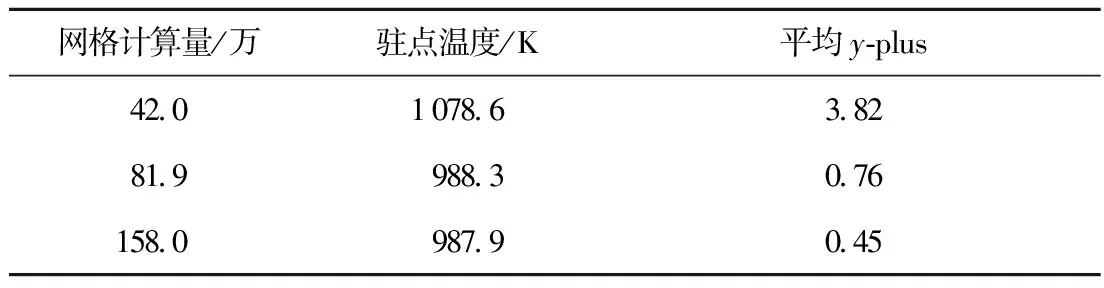
网格计算量/万驻点温度/K平均y⁃plus42010786382819988307615809879045

4.3 算例计算结果及分析

Culler A J等[16]指出气动热弹性分析时气动弹性系统响应与热传导之间巨大的时间尺度差别，故在气动热弹性分析中计算气动热时可以只考虑稳态气动热分布. 因此，本文在利用CFD计算气动热时仅仅考虑机翼的稳态气动热流分布情况. 所有翼型的网格拓扑结构和网格节点数均相同，为81.9万结构化网格，物面边界条件设置为辐射热平衡，辐射系数0.85.

为了定量衡量预测结果的好坏，采用均方根误差eNRMSE和最大值误差L∞，其公式为

(11)

(12)

式中：i为预测工况下的第i个节点的温度值；TROM为在Surrogate方法得到的降阶模型的预测值；TFull为CFD计算得到的温度值.

4.3.1 测试样本点相对平均误差分析

利用拉丁超立方设计方法lhsdesign函数在设计空间内随机选取10个测试样本点. 利用高超声速气动热模型降阶框架，针对10个测试样本点，翼面上表面温度平均相对误差如图6所示.

如图6所示，图6(a)、6(b)为利用lhsdesign函数选取样本点，分别选取Kriging和RBF代理模型构造方法的到的10个预测点翼面上表面平均相对误差图，对比图6(a)和6(b)可以看到：利用相同的采样方法，Kriging方法得到翼面上表面温度平均相对误差最大为5%，而RBF方法翼面上表面温度平均相对误差最大达到14%，对比图6(c)及6(d)同样发现利用相同的SLE采样方法，Kriging方法得到翼面上表面温度平均相对误差最大为1%，而RBF方法翼面上表面温度平均相对误差最大达到20%，在处理高超声速气动热预测时kriging方法精度要优于RBF方法. 同时对比图6(a)6(c)可知，取相同设计样本点，具有较好空间均匀性和投影均匀性的SLE方法得到翼面上表面温度平均相对误差均要小于lhsdesign方法，图6(c)的SLE采样方法翼面最大平均相对误差为1%，而图6(a)中lhsdesign方法最大平均相对误差达到5%，图6(c)中翼面各处翼面温度平均相对误差均小于图6(a)中翼面各处翼面温度平均相对误差.

4.3.2 测试样本点eNRSME和L∞误差分析

表2给出了不同采样方法(lhsdesign/SLE)和不同代理模型构造方法(Kriging/RBF)的10个测试点上、下翼面预测温度的eNRMSE和L∞误差分布情况，Avg为测试样本点的平均误差.

由表2对比可知，利用相同lhsdesign试验设计方法，Kriging方法的上下翼面预测温度eNRSME误差均小于RBF方法，上表面eNRSME平均误差Kriging方法为2.6%，小于RBF方法的7.6%，下表面eNRSME平均误差Kriging方法为3.1%，而RBF方法的eNRSME平均误差为9.6%；Kriging方法上表面翼面温度预测平均误差L∞为5.0%，而RBF方法上表面翼面温度预测平均误差L∞为10.2%，是Kriging方法的2倍. Kriging方法下表面翼面温度预测平均误差L∞为5.6%，同样小于RBF方法的温度平均误差7.7%. 同样对比分析得，相同的SLE试验设计方法，得到Kriging方法的上、下表面翼面温度预测eNRSME平均误差分别为0.85%,0.95%，远小于RBF方法的11.1%,12.6%，L∞平均误差1.9%,2.6%，小于RBF方法的15.6%,8.2%. 分析可知，Kriging方法在处理高超声速气动热预测时比RBF方法更具有优势.

表2 不同采样方法和不同代理模型构造方法测试点eNRMSE和L∞

Tab.2eNRSMEandL∞of test cases by different sampling methods and surrogate methods

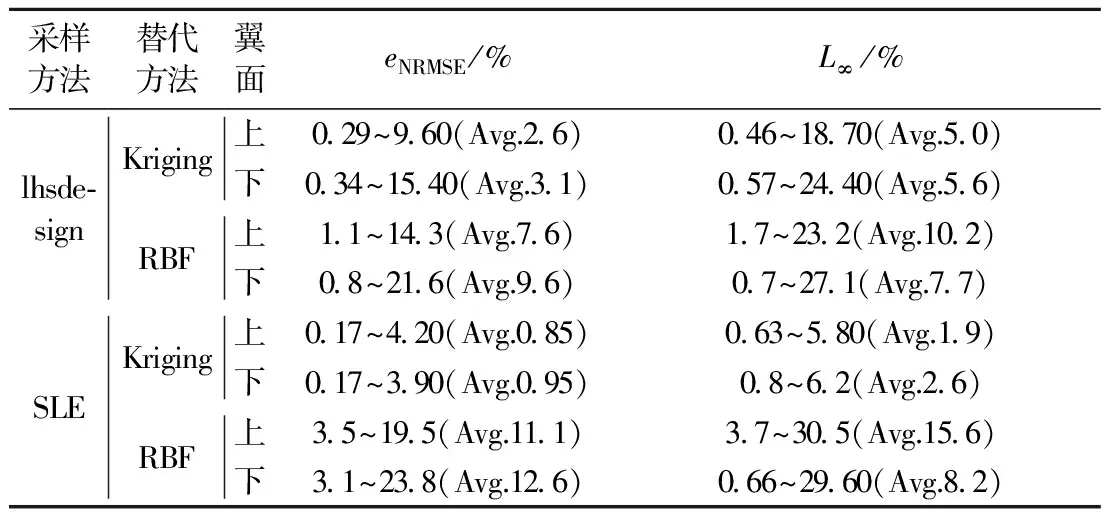
采样方法lhsde⁃signSLE替代方法KrigingRBFKrigingRBF翼面eNRMSE/%L∞/%上029～960(Avg．26)046～1870(Avg．50)下034～1540(Avg．31)057～2440(Avg．56)上11～143(Avg．76)17～232(Avg．102)下08～216(Avg．96)07～271(Avg．77)上017～420(Avg．085)063～580(Avg．19)下017～390(Avg．095)08～62(Avg．26)上35～195(Avg．111)37～305(Avg．156)下31～238(Avg．126)066～2960(Avg．82)

对比表2中的lhsdesign试验设计方法和SLE试验设计方法，利用相同的100个试验设计样本点，lhsdesign试验设计方法选取样本点，利用Kriging方法上下表面温度预测的eNRSME平均误差分别为2.6%和3.1%，L∞平均误差分别为5.0%和5.6%；SLE试验设计方法选取样本点，同样利用Kriging方法上下表面温度预测的eNRSME平均误差分别为0.85%和0.95%，L∞平均误差分别为1.9%和2.6%. 显然利用相同的试验设计方法，SLE试验设计方法方法能够明显提高降阶模型的预测精度.

4.3.3 典型算例结果与分析

选取典型工况下的上、下翼面温度CFD值与降阶模型(ROM)预测结果如图7所示，典型工况的飞行速度为1 798.1 m/s，高度为36 612.0 m，攻角为-1.0°. 如图7所示，选取SLE采样样本点分别利用Kriging方法和RBF方法构造翼面上下表面温度降阶模型. 通过ROM与对应真实值对比可知，kriging方法构造翼面上下表面如图7(a)和7(c)降阶模型预测结果均好于RBF方法，如图7(b)和7(d).

典型算例中Kriging方法构造高超声速气动热降阶模型预测结果与CFD计算温度值符合，降阶模型较好，具有较高的精度，验证了本文高超声速气动热降阶模型的可行性.

4.3.4 降阶模型效率分析

如表3所示，翼面上下表面各有4 800个节点，即利用代理模型方法构造4 800个近似拟合关系才能预测完整翼面温度分布. 利用数值计算(CFD)完成一个样本点的计算需约19.1 h. 选取100个设计样本点，利用Kriging方法构造高超声速气动热降阶模型耗时约45.94 s，而RBF耗时仅仅为0.009 s，这是由于Kriging方法构造近似关系是需要全局优化过程，这样比径向基函数(RBF)更耗时，构造4 800个近似拟合关系耗时远远大于RBF.

表3 降阶模型与数值计算对比

注：在i5-2320上计算，3.0 GHz， 4.00 GB RAM.

针对单个预测工况，利用Kriging方法的高超声速气动热降阶模型(ROM)预测耗时1.17 s，RBF方法构造的降阶模型(ROM)耗时1.03 s，两种方法构造的ROM预测耗时相近，与数值计算耗时约69 760 s(19.1 h)相比，本文建立的高超声速气动热降阶模型(ROM)具有很高的效率.

5 结论

① 提出一种基于代理模型的运用于高超声速气动热预测的模型降阶方法，建立了一种快速高效的高超声速气动热降阶模型框架. 典型三维算例表明，该模型降阶方法和降阶模型框架能够成功应用于高超声速气动热计算，具有较高的精度和效率；

② 对比lhsdesign计算试验方法和SLE计算试验方法构造高超声速气动热ROM，指出相同的设计样本点，SLE计算试验方法的气动热ROM具有更高的精度，空间均匀性和投影均匀性更好的SLE试验设计方法有助于提高气动热ROM的预测精度；对比Kriging方法和RBF方法精度和效率，指出Kriging方法在构造高超声速气动热降阶模型时更具有优势.

[1] 陈鑫，刘莉，李昱霖，等.高超声速飞行器翼面气动加热的工程计算方法[J].弹箭与制导学报，2013，33(3):133-137.

Chen Xin， Liu Li， Li Yunlin， et al. Engineering calculation of aerodynamic heating for airfoils of hypersonic vehicles[J]. Journal of Projectiles， Rockets， Missiles and Guidance， 2013，33(3)：133-137. (in Chinese)

[2] 车竞，唐硕，何开锋.类乘波体飞行器气动加热的工程计算方法[J]. 弹道学报，2006，18(4):58-65.

Che Jing， Tang Shuo， He Kaifeng. Engineering calculation of aerodynamic heating for quasi-waverider vehicle[J]. Journal of Ballistics， 2006， 18(4):58-65. (in Chinese)

[3] Mcnamara J J， Crowell A R. Approximate modeling of unsteady aerodynamics for hypersonic aeroelastic[J]. Journal of Aircraft， 2010，47(6):1932-1945.

[4] 王卫星，郭荣伟.基于边界层转捩的高超声速进气道特性研究[J].航空学报，2012，33(10):1772-1780.

Wang Weixing， Guo Rongwei. Study of flow characteristicsof hypersonic inlet based on boundary layer transition[J]. Acta Aeronautica et Astronautica Sinca, 2012，33(10):1772-1780. (in Chinese)

[5] Estruch S D，卜雪琴.高超声速下表面凸起干扰气动热实验研究[J].航空学报，2012，33(9):1578-1586.

Estruch S D， Bu Xueqin. Experimental investigation on hypersonic interface heating around surface protuberance[J]. Acta Aeronautica et Astronautica Sinca, 2012，33(9):1578-1586. (in Chinese)

[6] 杨华，姚卫星.基于径向基函数的机翼二维气动代理模型设计[J].计算力学学报，2008，25(6):797-802.

Yang Hua， Yao Weixing. 2D surrogate model of wing lift distribution based on radial function[J]. Chinese Journal of Compuational Mechanics， 2008，25(6):797-802. (in Chinese)

[7] 梁煜，程小全，郦正能，等.基于代理模型的气动外形平面参数多目标匹配设计[J].航空学报，2010，31(6):1141-1148.

Liang Yu， Cheng Xiaoquan， Li Zhengneng， et al. Multi-object aerodynamic configuration parameter design using kriging approximation[J]. Acta Aeronautica et Astronautica Sinca， 2010，31(6):1141-1148. (in Chinese)

[8] 夏露，王丹.基于Kriging自适应代理模型的气动优化方法[J].航空计算技术，2013，43(1):13-17.

Xia Lu， Wang Dan. Aerodynamic optimization method based on Kriging adaptive surrogate model[J]. Aeronautical Computing Technique， 2013，43(1):13-17. (in Chinese)

[9] Simpson T W， Booker A J， Ghosh D， et al. Approximation methods in multidisciplinary analysis and optimization: a panel discussion[J]. Structural and Multidisplinary Optimization， 2004，27(5):303-313.

[10] Zhu H G， Liu L， Long T， et al. A novel algorithm of maximin Latin Hypercube design using successive local emumeration[J]. Engineering Optimization， 2012，44(5):551-564.

[11] Mcnamara J J. Aeroelastic and aerothermoelastic behavior of two and three dimensional lifting surfaces in hypersonic flow[D]. Ann Arbor: University of Michigan， 2005.

[12] 董素君，居世超，齐玢，等.CFD-Fastran气动热计算模型及网格效应分析[J].航空计算技术，2011，41(2):40-42.

Dong Sujun， Ju Shichao， Qi Fen. et al. Model and grid dependency accuracy by CFD-FASTRAN software[J]. Aeronautical Computing Technique， 2011，41(2):40-42. (in Chinese)

[13] 阎超，禹建军，李君哲.热流CFD计算中格式和网格效应若干问题研究[J].空气动力学学报，2006，24(1):125-130.

Yan Chao， Yu Jianjun， Li Junzhe. Scheme effect and grid dependency in CFD computations of heat transfer[J]. Acta Aerodynamica Sinica, 2006，24(1):125-130. (in Chinese)

[14] 潘沙，冯定华，丁国昊，等.气动热数值模拟中的网格相关性及收敛[J].航空学报，2010，31(3):493-499.

Pan Sha， Feng Dinghua， Ding Guohao， et al. Grid dependency and convergence of hypersonic arothermal simulation[J]. Acta Aeronautica Et Astronautica Sinca， 2010，31(3)：493-499. (in Chinese)

[15] 覃文洁，胡春光，郭良平，等.近壁面网格尺寸对湍流计算的影响[J].北京理工大学学报，2006，26(5):388-392.

Qin Wenjie， Hu Chunguang， Guo Liangping， et al. Effect of near-wall grid size on turbulent flow solutions[J]. Transactions of Beijing Institude of Technology， 2006，26(5):388-392. (in Chinese)

[16] Culler A J， Mc. Namara J J. Studies on fluid-thermal-structural coupling for aerothermoelasticity in hypersonic flow[J]. AIAA Journal， 2010，48(5):1721-1738.

(责任编辑：刘雨)

A Reduced Order Modeling for Aerothermodynamic of Hypersonic Vehicles Based on Surrogate Method

CHEN Xin， LIU Li， YUE Zhen-jiang

(Key Laboratory of Dynamics and Control of Flight Vehicle， Ministry of Education，School of Aerospace Engineering， Beijing Institute of Technology， Beijing 100081， China)

Accurate and efficient estimation of aerodynamic heating is the basic prerequisite of theaerothermo-elasticity analysis. In order to solve the engineering adaptability problems of hypersonic aerothermodynamics calculation, numerical superprecision calculation and experimental investigation, a novel estimation method based on surrogate method for aerothermdynamic was proposed. Furthermore, a reduced order modeling (ROM) framework for aerothermodynamic was developed. Test results for the three-dimensional aerothermodynamics over a typical hypersonic control surface indicate that the average absolute errors,L∞and NRSME by SLE are all smaller than those by lhsdesign using the same samlping points and the same sorrogate methods. So the SLE sampling method can help to improve the precision of ROM. Comparing the results of ROMs for the three-dimensional aerothermodynamics over a hypersonic control surface, it is indicated that the precision of Kriging is better than that of RBF. The developed ROMs for the three-dimensional surface show higher precision and efficiency for hypersonic aerothermodynamic.

hypersonic; aerothermodynamic; surrogate model; reduced oder model

2014-06-11

国家自然科学基金资助项目(11372036)

陈鑫(1988—)，男，博士生，E-mail:blingkx@hotmail.com.

刘莉(1964—)，女，教授，博士生导师，E-mail:liuli@bit.edu.cn.

V 215.3； V 215.4

1001-0645(2016)04-0340-08

10.15918/j.tbit1001-0645.2016.04.002