DiffPRFs：一种面向随机森林的差分隐私保护算法

2016-11-24穆海蓉丁丽萍宋宇宁卢国庆

通信学报 2016年9期

关键词：决策树准确度差分

穆海蓉，丁丽萍，宋宇宁，卢国庆

（中国科学院软件研究所基础软件国家工程研究中心，北京 100190）

DiffPRFs：一种面向随机森林的差分隐私保护算法

穆海蓉，丁丽萍，宋宇宁，卢国庆

（中国科学院软件研究所基础软件国家工程研究中心，北京 100190）

提出一种基于随机森林的差分隐私保护算法DiffPRFs，在每一棵决策树的构建过程中采用指数机制选择分裂点和分裂属性，并根据拉普拉斯机制添加噪声。在整个算法过程中满足差分隐私保护需求，相对于已有算法，该方法无需对数据进行离散化预处理，消除了多维度大数据离散化预处理对于分类系统性能的消耗，便捷地实现分类并保持了较高的分类准确度。实验结果验证了本算法的有效性以及相较于其他分类算法的优势。

差分隐私；隐私保护；随机森林；数据挖掘

1 引言

随着信息技术应用的普及和深入，各种信息系统存储并且积累了丰富的数据。对于数据的需求极大促进了数据的发布、共享和分析。然而，数据集里通常包含着许多个人隐私信息，直接发布包含敏感信息的数据或是对已发布的数据进行分析都有可能造成个人隐私的泄露。隐私保护技术可以解决数据发布和数据分析带来的隐私威胁问题，防止用户的个人隐私信息或者敏感数据的泄露。

差分隐私[1～5]是Dwork在2006年针对统计数据库的隐私泄露问题提出的一种新的隐私定义。在此定义下，对数据集的计算处理结果对于某个具体记录的变化是不敏感的。所以，一个记录加入到数据集中所产生的隐私泄露风险被控制在极小的、可接受的范围内，攻击者无法通过观察计算结果而获取准确的个体信息。差分隐私能够解决传统隐私保护模型的2个缺陷：1) 差分隐私保护模型假设攻击者能掌握最大的背景知识，在这一最大背景知识假设下，差分隐私保护无需考虑攻击者所拥有的任何可能的背景知识；2) 它对隐私保护进行了严格的定义，并提供了量化评估方法。将差分隐私应用于数据挖掘中已有一些尝试，主要研究方向包括分类及回归分析[7～11]、top-k频繁模式挖掘[12,13]、聚类等。

分类[6]是一类重要的数据挖掘方法，在数据预测分析中起着关键作用。它找出描述和区分数据类或概念的模型(导出模型是基于对训练数据集的分析)，以便能够使用模型预测对象的类标号。导出模型可以用多重形式表示，如分类规则、决策树、数学公式或神经网络。决策树是分类模型的典型代表，它是一种树形的分类模型，树内节点表示在某个属性上的测试，而叶节点表示一个类。决策树归纳的学习和分类步骤是简单和快速的，一般而言，决策树分类器具有很好的准确率。决策树是许多商业规则归纳系统的基础，然而决策树本身以及相应的计数信息都有可能泄露用户隐私信息，存在个人隐私泄露的风险。

在决策树中应用差分隐私已经有了一些研究成果。文献[7]提出了基于交互式框架的应用差分隐私保护的决策树构建算法SuLQ-based ID3。文献[8]针对文献[7]噪声大的缺点，提出了利用指数机制挑选分裂属性的DiffP-ID3和DiffP-C4.5决策树分类方法。另外文献[9,10]基于非交互式框架，利用数据泛化（在数据挖掘研究中,将与挖掘任务相关的数据集从较低的概念层抽象到较高的概念层的处理过程）的方法，对数据进行匿名处理并发布，提高了分类的精度。文献[11]将差分隐私应用在决策树提升算法随机森林中，但提出的算法基于只能处理离散属性的 ID3决策树，因此需要对连续属性进行预处理后才能对数据集进行分类。

根据这些研究及存在的问题，本文提出一种基于差分隐私保护的随机森林分类方法。该方法相对于已有算法，消除了数据离散化的预处理步骤，便捷地实现分类并保持了较高的分类准确度，兼顾决策树分类的隐私性与可用性及分类实现的效率。

2 理论基础及相关研究

2.1 差分隐私背景知识

定义1 ε-差分隐私[1]。对于所有差别至多为一条记录的 2个数据集D1和D2，给定一个隐私算法F，Range(F)表示F的取值范围。若算法F提供ε-差分隐私保护，则对于所有S∈Range(F)，有

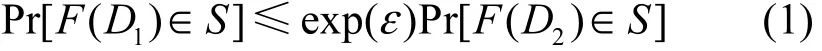
概率Pr[Es]表示事件Es的隐私被披露风险，由算法F随机性所控制，隐私预算ε表示隐私保护程度，ε越小隐私保护程度越高。

从定义可以看出，差分隐私技术限制了任意一条记录对算法F的输出结果的影响。定义从理论角度确保算法F满足ε-差分隐私，实现差分隐私保护则需要使用噪声机制。

噪声机制是实现差分隐私保护的主要技术，常用的噪声添加机制是拉普拉斯机制[4]和指数机制[5]。基于不同噪声机制且满足差分隐私的算法所需噪声大小与全局敏感性(global sensitive)相关。

定义 2 对于任意一个函数f:D→Rd，f的全局敏感性[4]定义为

数据集D1和D2之间至多相差一条记录。R表示映射的实数空间，d表示函数f的查询维度。

拉普拉斯机制通过拉普拉斯分布产生的噪声扰动真实输出值来实现差分隐私保护。

定理 1 拉普拉斯机制[4]，对于任一函数，若算法F的输出结果满足下列等式，则F满足ε-差分隐私保护。

定理2 指数机制[5]，设随机算法M输入为数据集D，输出为一实体对象r∈Range ，q(D, r)为可用性函数，Δq为函数q(D, r)的敏感度。若算法M以正比于的概率从Range中选择并输出r，那么算法M提供ε-差分隐私保护。

2.2 随机森林

随机森林[14]指的是利用多棵树对样本进行训练并预测的一种分类器。简单来说，随机森林由多棵决策树构成，并且其输出的类别是由单棵决策树输出的类别的众数而定。Leo和 Adele最早提出了执行随机森林的关键算法。Amit、Gemen和Ho Tim Kam各自独立地介绍了特征随机选择的思想，并且运用了Breiman的bootstrap aggregating思想构建了控制方差的决策树集合。

2.2.1 训练方法与分类方法

随机森林的训练和分类过程可以总结如下。

输入：训练数据集S，属性集F，分类属性集C生成的决策树的数量t，每棵树的深度d，每个节点使用到的属性数量f

终止条件：节点全部记录的分类属性一致，或达到最大深度d

输出：随机森林

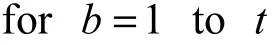
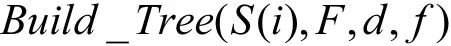
2) 随机地从属性集F中选取f个属性；

3) 从 f个属性中寻找分类效果最好的属性 k作为分裂属性，将当前节点上样本第k维属性按照分类结果被划分到子节点

利用随机森林的预测过程如下。

对于第k棵树：

1) 从当前树的根节点开始，根据当前节点的分类结果集合，判断是进入哪个子节点，直到到达某个叶子节点，并输出预测值；

2) 重复执行 1)直到所有 t棵树都输出了预测值。对于分类问题，输出为所有树中预测概率总和最大的那一个类，即对每个c(j)的p进行累计。

2.2.2 随机森林的特点

随机森林的优点如下。

1) 在大数据集上表现良好，2个随机性的引入使随机森林不容易陷入过度拟合，并且具有很好的抗噪声能力。

2) 能够处理很高维度的数据，它可以处理非常多的输入变量，并确定最重要的变量，因此被认为是一个不错的降维方法。

3) 训练过程速度快，可以得到属性重要性排序。

4) 容易做成并行化方法。

5) 实现比较简单。

随机森林的缺点如下。

1) 随机森林在解决回归问题时因为不能给出一个连续型的输出，导致其并没有像分类中表现的那么好。当进行回归时，随机森林不能够作出超越训练集数据范围的预测，这可能导致在对某些含有特定噪声的数据进行建模时出现过度拟合。

2) 随机森林让统计建模者感到几乎无法控制模型内部的运行，只能在不同的参数和随机种子之间进行尝试。

2.3 已有研究的对比

本课题重点关注决策树分类与差分隐私的结合。由于分类属性高维度的特点，给差分隐私保护技术在决策树构建过程中的应用带来了很大的挑战。

表1展示了当前在交互式框架与非交互式框架下，基于差分隐私的决策树分类方法的研究进展。

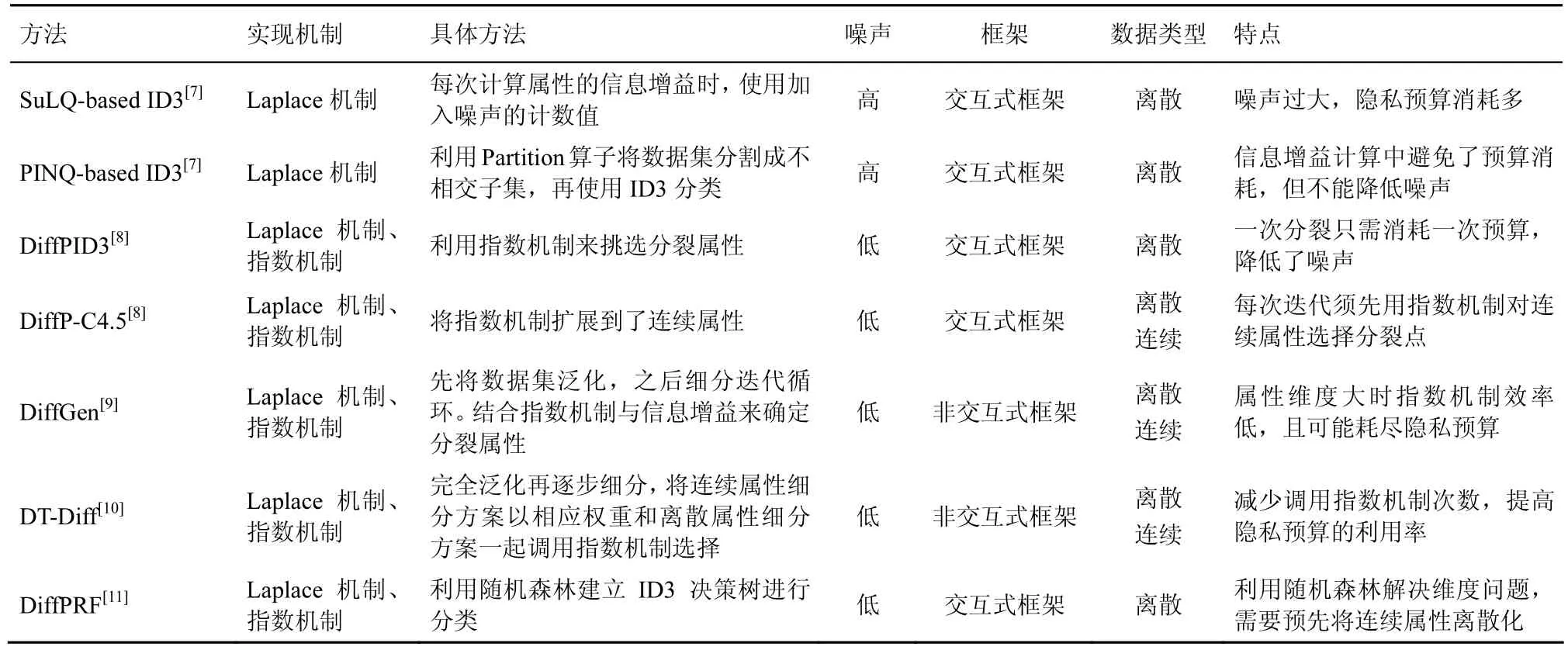
表1 差分隐私下分类方法对比分析

SuLQ-based ID3算法[7]基于交互式框架，其基本思想是在每次计算属性的信息增益时，使用加入噪声的计数值，最终生成相应的决策树。从对模拟数据集的实验结果来看，在隐私保护预算小于 1的情况下，该算法相对于无隐私保护功能的ID3算法，其预测准确率大约降低了30%[8]。

Friedman 和 Schuster 基于 PINQ 平台对SuLQ-based ID3算法进行了改进，利用其中的Partition算子将数据集分割成不相交的子集，然后再实现ID3算法。但由于每个查询的预算相对很小，所以无法显著降低SuLQ-based ID3所引入的噪声。Friedman和Schuster 进一步在ID3算法中应用指数机制实现差分隐私保护，提出了DiffP-ID3算法[8]，有效降低了噪声。另外，通过将离散属性的处理扩展到连续属性，Friedman 和 Schuster 还提出了DiffP-C4.5算法[8]。DiffP-C4.5算法的缺点在于，在每一次迭代中必须先用指数机制对所有连续属性选择分裂点，然后将所得结果与全部离散属性一起再次通过指数机制选择最终的分裂方案，由于每次迭代需要调用指数机制2次，因此消耗了过多的隐私保护预算。

DiffGen算法[9]结合泛化(generalization)技术与自顶向下分割技术，结合指数机制与信息增益来确定分裂属性。自顶向下划分数据集D中所有记录到决策树的叶子节点，然后对叶子节点添加拉普拉斯噪声。实验结果表明，DiffGen方法的分类精度高于SuLQ-based ID3和DiffP-C4.5方法，但是由于该方法每一个分类属性对应一个分类树，当数据集中的分类属性维度非常大时，该方法不得不维护大量的分类树，导致基于指数机制的选择方法效率很低，并且有可能耗尽隐私预算。

DT_Diff算法[10]对 DiffGen和DiffP-C4.5中的问题进行了改进，将所有连续属性细分方案乘以相应的权重后和离散属性细分方案一起构成候选方案集，再调用指数机制来选择细分方案。这样做减少了调用指数机制的次数，从而提高了隐私预算的利用率，使在给定的隐私预算下，数据集能够更大程度地精确化，从而提高分类模型的准确率。

Abhijit Patil和Sanjay Singh将差分隐私应用在决策树提升算法随机森林中，提出了DiffPRF算法[11]，但提出算法基于只能处理离散属性的ID3决策树，因此需要先对连续属性进行预处理后才能通过该算法对数据集进行分类。

上述几种方法无论是基于交互式框架还是非交互式框架，其核心技术均为决策树和拉普拉斯/指数机制，并且使用信息增益来选择分裂规则。但是它们或多或少存在一些问题，主要有2点不足：1)当数据集中分类属性的维度非常大时，导致基于指数机制的选择方法效率很低；2)隐私预算分配策略过于单一，急需有效的策略。因此，如何对具有高维度分类属性的数据集进行分类，以及如何设计有效的隐私预算分配策略，是未来的研究方向。本文提出的方法基于随机森林的特性，提高了对大数据集、高维数据集分类时使用指数机制的效率，并且支持直接对连续属性的分类，而不需先对高维连续属性进行离散化，实验结果验证了本算法有较高的分类准确度。

3 算法及性能分析

本文提出一种差分隐私下的随机森林分类方法，将差分隐私应用在随机森林当中，在可接受的分类准确度下尽可能保护数据的隐私。

3.1 DiffPRFs算法框架

差分隐私下的随机森林建立过程描述如下。

输入：训练数据集S，属性集F，分类属性集C，隐私预算B，生成的决策树的数量t，每棵树的深度d，每个节点使用到的属性数量f

终止条件：节点全部记录的分类属性一致，达到最大深度d或隐私预算耗尽

输出：满足ε-差分隐私的随机森林

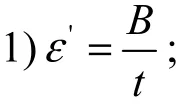
2) for b=1 to t

3) 从S中有放回的随机选取大小为|S|的训练集S(i)；

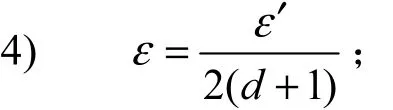
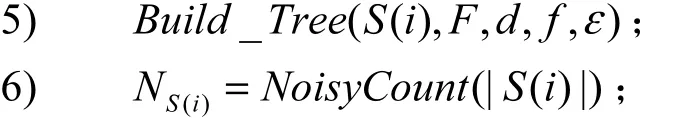
8) 随机地从属性集F中选取f个属性；

9) 若随机选择的f个属性中包含n连续属性，执行步骤10)，否则，直接执行步骤11)；

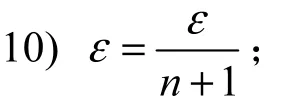
用以下概率选择每个连续属性的分裂点

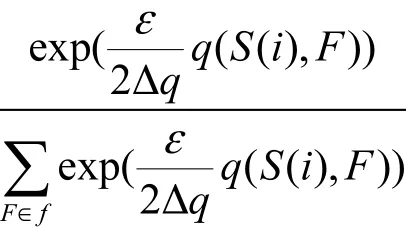
12) 按照分裂属性将当前节点分为2个子节点

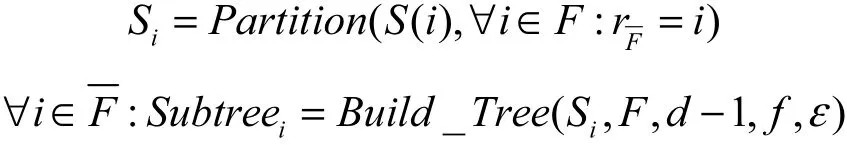
通过以上算法建立的随机森林对测试集进行分类的过程描述如下。

输出：测试集中每条记录的分类结果

1) 对于测试集T每一条记录x；

2) for b=1 to t；

3) 从当前树的根节点开始，根据当前节点的分类结果集合，判断是进入哪个子节点，直到到达某个叶子节点;

3.2 算法实现细节

差分隐私下的随机森林分类方法DiffPRFs分2步来实施，具体步骤如下。

1) 通过训练数据集建立随机森林

输入：训练数据集S，属性集F，分类属性集C，隐私预算B，生成的决策树的数量t，每棵树的深度d

终止条件：节点全部记录的分类属性一致，达到最大深度d或隐私预算耗尽

输出：满足ε-差分隐私的随机森林

首先根据参数中树的棵数，将隐私预算B均分给t棵树；之后按照同样的规则递归地生成每一棵决策树。生成决策树的策略如下。

2) 利用建立的随机森林对测试数据集进行分类

输出：测试集中每条记录的分类结果

对测试集中的每一条记录，应用森林中的每一棵树对其进行分类预测。在每一个节点上都根据当前节点的分类结果集合判断该条记录应进入哪一个子节点，直到到达某个叶子节点，通过当前叶子节点ε获得一个预测值。根据森林中每棵树的预测结果得到所有预测结果中概率最大的那个分类结果。之后输出所有记录的分类结果。

由于随机森林在大数据集上表现良好，能够处理很高维度（即属性较多）的数据，并且训练速度快，这些优点能够很好地解决此前方法中问题，实现对高维度大规模数据的高准确度预测分类。

3) 可用性函数

设S为数据集，s=|S|，分类属性C有m个不同取值，即定义了m个不同的类

在算法中为了度量用每个属性进行分类、用不同的分裂点对连续属性进行划分的可用性水平，选用以下2种可用性函数。

一种是基于信息增益[15]的可用性函数，即

计算数据集S的熵为

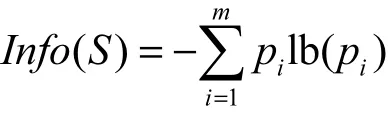
其中，pi是S中任意元素属于类Ci的非零概率，使用估计。

假设按属性A划分S中的元组，A根据训练数据集有v个不同值使用属性A将S划分为u个子集，基于按A划分对S中的元组分类所需的期望信息为

用其分类产生的信息增益为

3.3 算法隐私性分析

DiffPRFs算法中将给定的隐私预算B首先平均分给森林中的每一棵树，由于每棵树中的样本是随机选择的，因此会有一定的交叉，根据差分隐私序列组合性，随机消耗的隐私预算为每棵决策树消耗隐私预算的叠加。树的每一层包括叶子节点都是相同的数据集，因此平均分配了隐私预算。每一层因为在不相交的数据集上进行技术和分裂，因此每个节点分配的隐私预算就是这一层的隐私预算。根据差分隐私的并行组合性[16]，节点的隐私预算不进行累加。分给每个节点的隐私预算一半用来估计该节点的实例数(应用拉普拉斯机制)，另一半需要根据该节点是中间节点还是叶节点进行区分，若该节点为叶节点，需要用剩下的这一半隐私预算来确定类计数，同样使用拉普拉斯机制对计数值添加噪声。若该节点为中间节点，假设从F个属性中随机选出的f个属性有n个连续属性，将隐私预算均分为n+1份，选择每个连续属性的分裂点，之后从所有属性中选择出该节点的分裂属性，选择分裂点与分裂属性时均使用指数机制进行选择，每次使用指数机制消耗的隐私预算为，按照差分隐私的序列组合性[16]，多次指数机制消耗的隐私预算为各次的叠加。所以，算法所消耗的全部隐私预算不大于B，它具有ε−差分隐私性。

生成的这些决策树组成满足ε−差分隐私的随机森林。每棵树的训练样本是随机选择的，树中每个节点属性也是随机选择的。每个节点上属性的个数一般为整个属性个数的均方根，这样也就一定程度上解决了高维度带来的问题。

4 实验结果

4.1 实验环境及数据

本文的分类器数据处理、训练和测试算法均采用python2.7实现。实验环境为OS X Yosemite四核2.8 GHz，内存 16 GB 1 600 MHz DDR3。本文以 UCI机器学习数据库中的 adult数据集检验算法的有效性，并在相同的测试条件下与其他算法进行比较。UCI adult包含训练集与测试集，其中，包含6个连续属性与8个离散属性。分类属性income level分为“≤50k”与“≥50k”2类。训练集中包含45 222条记录，测试集中包含15 060条记录。

4.2 实际数据集测试结果

在ε=0.05、0.1、0.25、0.5、0.75、1、2，t=25，每棵树的深度d=3、4、5、6、7，可用性函数使用信息增益和最大类频数和的设置下进行了多组实验。每组实验在给定的隐私预算和树的深度下使用DiffPRFs算法对训练数据集建立随机森林分类模型，并用该模型对测试数据集进行分类，记录相应的分类准确度。每组实验进行5次，以5次结果平均值作为最终结果。实验结果如图1所示。

从图1中可以看出，当ε取值较小的时候，由训练集训练出的随机森林分类器分类准确度较低，而随着ε取值增大，分类正确率虽然偶有波动，但总体趋势是逐渐提高的。这是因为随着ε逐渐增大，较优的方案被选择的几率也随之提高。随着决策树深度的增加，记录经过了更多属性的筛选，分类的准确度也逐渐提高。另外2种可用性函数的准确度也非常类似，趋势上也均符合预期。

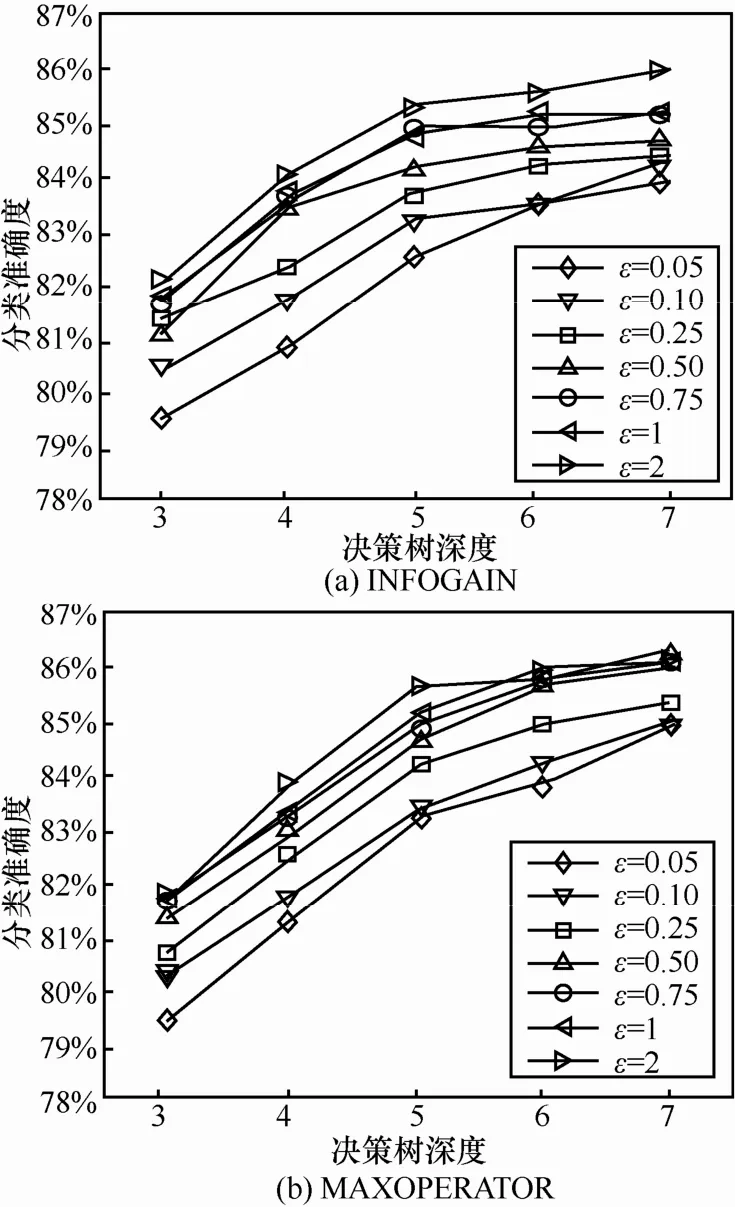
图1 不同条件下的DiffPRFs分类准确度

本文还设定d=5，ε=0.1、0.25、0.5、0.75、1，t=25，将提出的算法 DiffPRFs与不加入差分隐私的随机森林算法、DiffPRF算法进行比较。其中不加差分隐私的随机森林算法由本文提出的算法修改实现、DiffPRF算法同等条件下的分类准确度由文献[11]提供。实验结果如图2所示。

图2 与随机森林及DiffPRF的比较

通过与随机森林算法以及DiffPRF算法的比较可以看出，本文提出的算法可以达到较高的分类准确度。虽然在构建决策树的过程中消耗了一定的隐私预算处理连续属性，但不需对连续属性进行离散化预处理，面对大规模高维度的数据，将连续属性离散化十分费时费力，因此在构建决策树的过程中进行直接处理一定程度上提高了分类的效率。在这样的情况下分类准确度相对于DiffPRF算法只降低了非常有限的一点，这是可以接受的。本算法在保证数据安全性的前提下，提供了更加便捷高效的分类方法，连续属性与离散属性都可以直接处理，同时也保证了数据的可用性。

5 结束语

本文提出了一种面向随机森林的差分隐私保护算法DiffPRFs，用于对数据构建分类器并且进行分类。通过对DiffPRF算法中指数机制方案选择的改进，使构建的随机森林可以在决策树构建过程中有效地处理连续属性，而不需要在构造随机森林前预先进行处理，避免了对高维度、大规模数据进行离散化的高额成本。实验结果证明本算法相较于DiffPRFs算法的分类准确度并没有明显降低，从而显示了该算法的优越性。当然由于建立了多棵决策树，每棵树分配的隐私预算相对较少，一定程度上影响了分类的准确度，接下来的工作中会继续尝试对算法进行进一步优化，提升分类的准确度；也会尝试在其他一些决策树的提升算法中应用差分隐私，以期得到更好的分类准确度。

[1] DWORK C. Differential privacy[C]//The 33rd International Colloquium on Automata, Languages and Programming. Berlin:Spinger-Verlag, 2006: 1-12.

[2] DWORK C. A firm foundation for private data analysis[J]. Communications of the ACM, 2011, 54(1):86-95.

[3] 张啸剑, 孟小峰. 面向数据发布和分析的差分隐私保护[J]. 计算机学报, 2014, 37(4): 927-949.ZHANG X J, MENG X F. Differential privacy in data publication and analysis[J]. Chinese Journal of Computers, 2014, 37(4): 927-949.

[4] DWORK C, MCSHERRY F, NISSIM K, et al. Calibrating noise to sensitivity in private data analysis[M]//Theory of Cryptography.Springer Berlin Heidelberg, 2006: 265-284.

[5] MCSHERRY F, TALWAR K. Mechanism design via differential privacy[C]//Foundations of Computer Science. 2007: 94-103.

[6] 范明, 孟小峰, 译. 数据挖掘: 概念与技术[M]. 北京: 机械工业出版社, 2012.FAN M MENG X F. Data minify: concepts and techniques[M]. Beijing China Machine Press, 2012.

[7] BLUM A, DWORK C, MCSHERRY F, et al. Practical privacy: the SuLQ framework[C]//The 24th ACM SIGMOD-SIGACT-SIGART Symposium on Principles of Database Systems. ACM, 2005:128-138.

[8] FRIEDMAN A, SCHUSTER A. Data mining with differential privacy[C]//The 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM, 2010: 493-502.

[9] MOHAMMED N, CHEN R, FUNG B, et al. Differentially private data release for data mining[C]//The 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM,2011: 493-501.

[10] ZHU T, XIONG P, XIANG Y, et al. An effective deferentially private data releasing algorithm for decision tree[C]//Trust, Security and Privacy in Computing and Communications (TrustCom), 2013 12th IEEE International Conference. IEEE, 2013: 388-395.

[11] PATIL A, SINGH S. Differential private random forest[C]//Advances in Computing, Communications and Informatics International Conference. IEEE, 2014: 2623-2630.

[12] 丁丽萍, 卢国庆. 面向频繁模式挖掘的差分隐私保护研究综述[J].通信学报, 2014, 35(10): 200-209.DING L P, LU G Q. Survey of differential privacy in frequent pattern minify[J]. Journal on Communications, 2014, 35(10): 200-209.

[13] 卢国庆, 张啸剑, 丁丽萍, 等. 差分隐私下的一种频繁序列模式挖掘方法[J]. 计算机研究与发展, 2015, 52(12): 2789-2801.LU G Q, ZHANG X J, DING L P, et al. Frequent sequential pattern mining under differential privacy[J]. Journal of Computer Research and Development, 2015, 52(12) : 2789-2801.

[14] BREIMAN L. Random forests[J]. Machine Learning, 2001, 45(1):5-32.

[15] QUINLAN J R. Induction of decision trees[M]//Readings in Knowledge Acquisition and Learning．San Francisco: Morgan Kaufmann Publishers Inc，1993: 349-361．

[16] MCSHERRY F. Privacy integrated queries: an extensible platform for privacy-preserving data analysis[C]//The 2009 ACM SIGMOD International Conference on Management of Data. ACM, 2009: 19-30.

DiffPRFs: random forest under differential privacy

MU Hai-rong, DING Li-ping, SONG Yu-ning, LU Guo-qing
(National Engineering Research Center of Fundamental Software, Institute of Software, Chinese Academy of Sciences, Beijing 100190, China)

A differential privacy algorithm DiffPRFs based on random forests was proposed. Exponential mechanism was used to select split point and split attribute in each decision tree building process, and noise was added according to Laplace mechanism. Differential privacy protection requirement was satisfied through overall process. Compared to existed algorithms, the proposed method does not require pre-discretization of continuous attributes which significantly reduces the performance cost of preprocessing in large multi-dimensional dataset. Classification is achieved conveniently and efficiently while maintains the high accuracy. Experimental results demonstrate the effectiveness and superiority of the algorithm compared to other classification algorithms.

differential privacy, privacy protection, random forest, data mining

The National High Technology Research and Development Program of China(863 Program) (No.2015AA016003)

TP309.2

10.11959/j.issn.1000-436x.2016169

2016-01-11；

2016-03-16

国家高技术研究发展计划（“863”计划）基金资助项目（No.2015AA016003）