混合信道下LDPC码稳定条件分析及度序列优化

2016-11-24孙康宁马林华茹乐范文同胡星黄绍城

通信学报 2016年9期

孙康宁，马林华,2，茹乐，范文同，胡星，黄绍城

（1. 空军工程大学航空航天工程学院，陕西西安 710038；2. 西安电子科技大学综合业务网国家重点实验室，陕西西安 710071；3. 解放军94626部队，福建福州 350002）

孙康宁1，马林华1,2，茹乐1，范文同3，胡星1，黄绍城1

在高斯噪声和随机删除同时存在的背景下，提出LDPC码度序列的稳定收敛条件，理论证明了高斯信道下阈值较高的度序列不适用于混合信道，并仿真验证了该结论。将随机粒子群算法和模拟退火算法相结合，不同删除概率下寻找到了一些高阈值混合信道的度序列，删除概率为40%时，度序列信噪比阈值最大可提高1.615 9 dB，适用于光记录、伴随窄带阻塞干扰的跳频通信等混合信道环境。

低密度奇偶校验码；混合信道；高斯近似；随机粒子群优化；模拟退火

1 引言

低密度奇偶校验（LDPC, low density parity check）码由于其逼近香农限的优异性能[1～4]，已经成为一种应用范围广泛的信道编码。设计性能优异的LDPC码的一个关键因素就是寻找合适的高阈值度序列，且满足稳定收敛条件[5]。LDPC的纠错性能具有门限效应，即当实际信噪比大于度序列的阈值σ时，随着码字长度的增大并经过一定次数的迭代后，错误概率可以小于任意的数ε。

当前，在各类信道上的度序列设计已经取得了丰硕的成果，Richardson等[5]对高斯信道、二进制对称信道、二进制删除信道下的LDPC码度序列设计进行了研究，提出了广义的稳定收敛条件，并给出了一些高斯信道下优秀的度序列。Hou等[6]提出了瑞利信道下的度序列稳定收敛条件，仿真了一些瑞利信道下优秀的度序列。然而，针对高斯噪声和随机删除同时存在的混合信道的LDPC码度序列却一直未被人们所关注，适合不同删除概率的混合信道度序列一直未被提出，这种信道广泛地存在于光记录、伴随窄带阻塞干扰的跳频通信等应用环境中，且在工程实际中一般都是运用高斯信道下性能优异的度序列[7～10]。

本文首先从理论和仿真实验这2个方面证明了高斯信道下性能好的度序列在混合信道下性能不一定好，尤其是在高删除概率时，性能退化较为严重，因此在该环境下设计优化的度序列是很有必要的。其次，结合混合信道下的高斯近似方法[11,12]，利用随机粒子群与模拟退火相结合的寻优算法[13,14]，对目标函数进行合理的降维，在不同删除概率的条件下搜索出一些阈值较高的度序列，较高斯信道下阈值较高的度序列应用在混合信道时优势明显,可以较好地适应实际中的光记录及伴随窄带阻塞干扰的跳频通信环境。

2 混合信道特性

在光记录环境中，由于光介质表面划痕的存在，会在进行激光激励写入操作时造成信息无法写入，发生数据删除，加上热表面高斯噪声，严重影响读取时的数据恢复能力[11]；在带有窄带阻塞干扰的跳频通信中，由于在部分频带的强干扰压制，使在这些频点传输的数据严重失真，在接收端通过信道估计手段可确定受干扰的频点，从而将这些频点传输的信息删除，需要利用从其他频点接收到数据进行纠错恢复。上述2种环境的信道均可被称为混合信道，如图1所示。

其中，x表示二进制源信息{0,1}；c表示LDPC码编码并经过BPSK映射的信息{+1,−1}；n表示加性高斯白噪声表示乘性删除噪声，为未进行译码迭代时信道初始删除概率；r为信道输出值；表示经 LDPC码译码器译码并进行了 BPSK解调的{0,1}信息。信道输出数值r的概率密度函数如图2所示，其中表示c=±1时译码器前端接收信号数值的概率密度函数为冲击函数。当r=0时，一种情况是未被删除的，由于高斯噪声造成的信道输出值为 0；另一种情况是该码元被删除的，在译码端被视为0。

因此，信道输出概率密度函数的 LLR(对数似然比)可以表示为

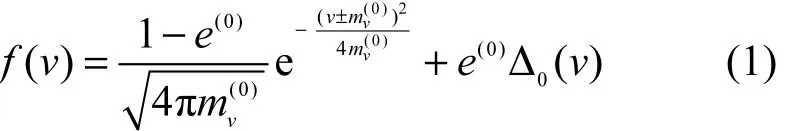
本文在进行高斯近似分析及稳定收敛条件推导时均基于上述信道。

3 混合信道下非规则码的高斯近似

Jeongseok等[11]把高斯近似拓展到了混合信道，利用该方法在混合信道下计算度序列阈值，混合信道下高斯近似简述如下。

为了描述非规则码度序列，设

其中，λ(x)、ρ(x)分别为变量节点和校验节点的度分布，λi和ρi分别代表与度为i的变量节点、校验节点相连的边占总边数的比率。

由于概率密度函数满足对称性条件，则第k次迭代时，变量消息和校验消息u(k)的分布，分别近似服从和分布，其中，为k次迭代时变量（校验）节点消息的平均值，并且可得为噪声方差

与高斯信道下的高斯近似不同，随机删除的存在导致了混合信道下校验节点消息均值回归方程[11]变为

其中，φ(x)为定义的单调递减函数如下

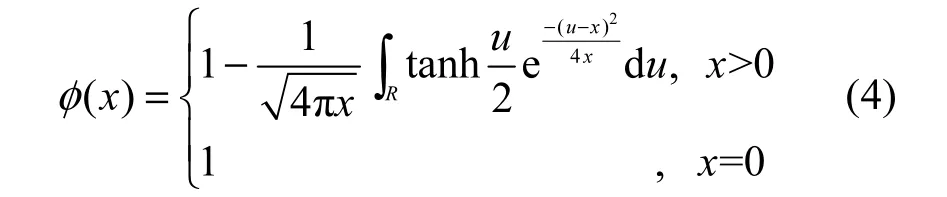
4 混合信道下度序列的稳定收敛条件

Richardson等[5]提出了LDPC码的广义稳定收敛条件，具体如下。

必要性：如果度序列满足λ′(0)ρ′(1) gt;er，存在一个常数，当译码迭代次数，错误概率

充分性：如果度序列满足λ′(0)ρ′(1) lt;er，存在一个常数，当译码迭代次数，错误概率

也就是说，如果给定的度序列不满足所在信道的稳定收敛条件，其误码率会存在一个下限，影响LDPC码的纠错性能。

根据上述理论，本文给出了混合信道下LDPC码度序列稳定性条件，过程如下。

根据广义稳定收敛条件[5]得

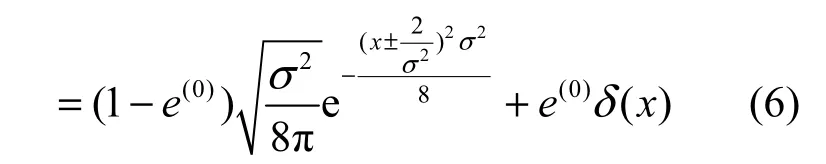
混合信道

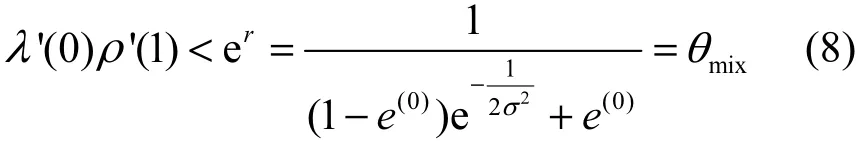
由式(9)可以推断出：高斯信道下性能较好的度序列在混合信道条件下不一定是最优的，尤其是在高删除概率条件下。

下面通过混合信道密度进化的高斯近似，给出混合信道下编码效率为0.5的2个度序列在不同删除概率条件下与香农限距离的变化曲线，如图3所示。

度序列A为

度序列B为

图3 不同删除概率下与香农限的距离

从图3中可以看出，度序列A虽然在没有数据删除的高斯信道下性能较度序列B差，但是随着删除概率的提高，其性能逐渐超越度序列B。此变化趋势验证了上述推导的结论。

5 混合随机粒子群优化

李森、孙艺等[13,14]提出了一种混合随机粒子群算法，能确保解为全局最优解，在高斯信道下寻找到了更接近香农限的度序列，本文将此方法用于寻找混合信道下优化的度序列。其基本思想就是将随机粒子群算法与模拟退火算法结合，对停止进化的粒子以高斯变异的方法产生一个邻域内的变异点，以此进行模拟退火寻找最优点。

The procedure for the sample preparation of flavonoids was the same as that for alkaloids, except that the extraction solvent of methanol (40 mL) was used, and the volumes of the successive filtrate and injection were 20 mL and 20 mL, respectively.

随机粒子群算法的主要计算式如下

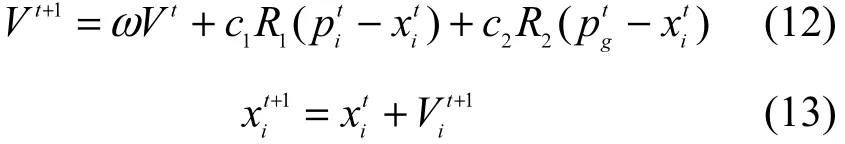
实现过程：1) 初始化各参数及粒子的位置，并计算各粒子的适应值 f(⋅)，也称为目标函数；2) 对进行计算，当并且其他的粒子也无法找到更优解时，则会出现粒子聚集的现象，丧失搜索能力，此时为改善此现象，记录最好位置pg，并在搜索范围内重新随机生成粒子j的新位置其他粒子仍然按照式(12)、式(13)进化；3) 最后，若满足停止条件，则输出解，否则返回过程2)，继续进行寻优。

为了使随机生成粒子j的新位置更加趋近于最优解，本文利用具有局部最佳逃离能力的模拟退火(SA)算法更新位置。

停止进化粒子的模拟退火更新过程如下。

在进行模拟退火更新时需引入一个高斯变异波动方差值δ控制新位置的范围，避免新位置的过分偏离，根据度序列约束条件，本文设定

文献[15,16]中提出，校验节点的度序列的性能限影响不大，且一般只有2～3项，本文在优化过程中选取具有2个非零项的校验节点度序列，根据已知的码率和寻找到的最优变量节点的度分布即可推算出校验节点度分布，以此降低搜索难度，解空间的围数降至，简化了粒子群优化的目标函数。本文粒子群优化问题变为寻找，其中，f(λ)为最小化目标函数，为利用混合信道下高斯近似得到的给定度序列的阈值。

6 混合信道高阈值度序列

本文搜索到了一些删除概率为0.1～0.4的混合信道条件下阈值较高的度序列，与文献[5]中的度序列在混合信道时的阈值进行了对比，并将阈值的提高转化成信噪比阈值之差ΔSNR的形式进行表示。σ表示本文搜索到的优化的度序列在一定删除概率的混合信道下的阈值，σ*表示文献[5]中度序列在一定删除概率的混合信道下的阈值。

由表1～表4可知，本文搜索到的度序列在各个删除概率的混合信道下阈值均优于文献[5]中提出的度序列，尤其是在高删除概率时，度序列的信噪比容量最大提升了 1.615 9 dB。此外，可以观察到随着变量节点最大度数的提高，优化度序列性能提升的幅度降低，这是因为最大度数越大，度序列性能越接近香农限，可提高的空间也就越小。但最大度数的提高带来的是校验矩阵平均列重的增大，提高了编译码复杂度，因此在实际应用中应当根据硬件特点合理选择度序列。

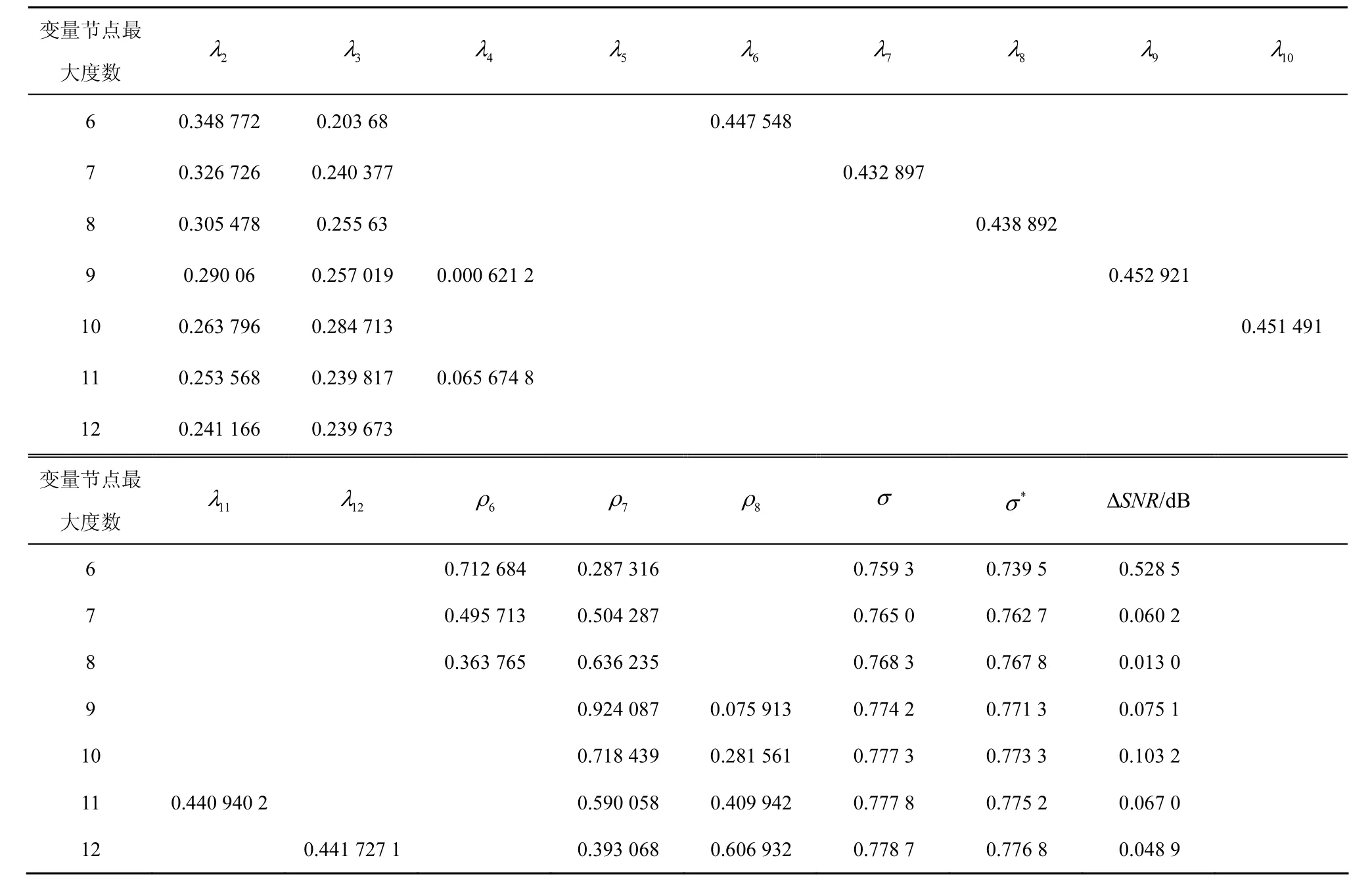
表1 10%删除概率的混合信道下优秀的度序列

表2 20%删除概率的混合信道下优秀的度序列

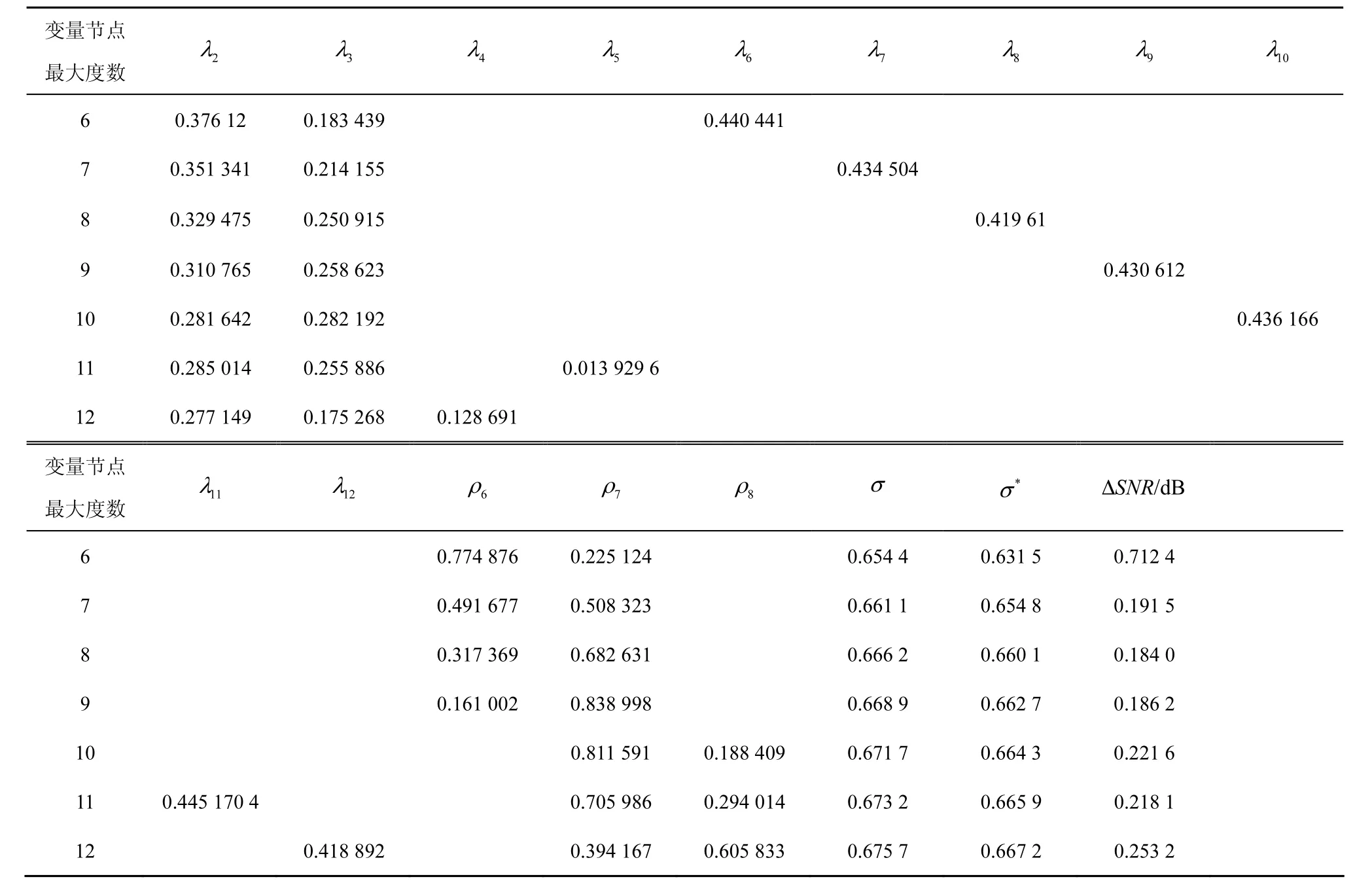
表3 30%删除概率的混合信道下优秀的度序列

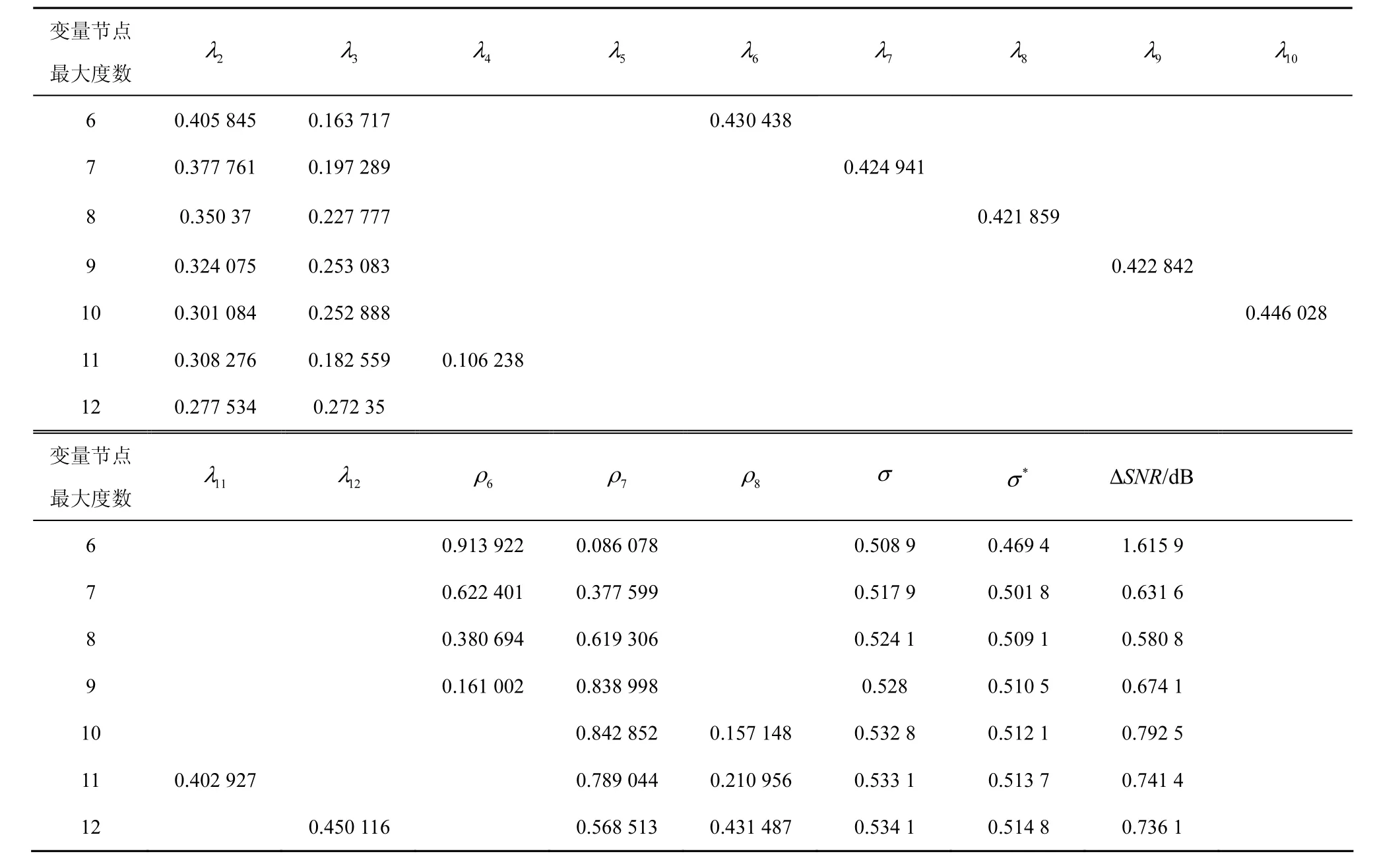
表4 40%删除概率的混合信道下优秀的度序列

7 结束语

混合信道下LDPC码的相关设计问题一直以来未能引起研究人员的足够重视，本文通过对混合信道下LDPC码度序列的研究，提出了该信道下度序列稳定收敛条件，并与高斯信道度序列稳定收敛条件进行了对比，得出了高斯信道下性能较好的度序列在混合信道条件下不一定最优的结论，并进行了仿真验证。通过混合粒子群算法进行寻优，寻找到了一些在不同删除概率的混合信道下阈值较高的度序列。这些度序列适用于光记录环境及伴随有窄带阻塞干扰的跳频通信环境，能有效提高这些应用的抗噪声性能。

[1] GALLAGER R G. Low density parity-check codes[J]. IEEE Transactions on Information Theory, 1962, 8(1): 21-28.

[2] MACKEY D J C. Good error-correcting codes based on very sparse matrices[J]. IEEE Transactions on Information Theory, 1999, 45:399-431.

[3] HOU Y, LIU R, PENG H, et al. High throughput pipeline decoder for LDPC convolutional codes on GPU[J]. IEEE Communication Letters,2015, 19(12):2066-2069.

[4] 赵明, 张晓林. 基于改进2-D GRS码的QC-LDPC码高效构造[J].通信学报, 2015,36(2):1-7.ZHAO M, ZHANG X L. Novel construction of QC-LDPC codes with modified 2-D GRS codes[J]. Journal on Communications, 2015,36(2):1-7.

[5] RICHARDSON T J, SHOKROLLAHI M A, URBANKE R. Design of capacity-approaching irregular low-density parity-check codes[J].IEEE Transaction on Information Theory, 2001, 47(2):619-637.

[6] HOU J L, PAUL H, SIEGEL B. Performance analysis and code optimization of low density-parity check codes on rayleigh fading channels[J]. IEEE Journal on Selected Area in Communication, 2001,19(5):126-147.

[7] YANG K Z, ZHANG B N, WANG H X. The performance analysis of LDPC coded SFH/BPSK anti-jamming system[C]//International Conference on Wireless Communications amp; Signal Processing. Nanjing,China, 2015:1-5.

[8] IMMINK K A S. A survey of codes for optical disk recording[J]. IEEE Journal on Selected Areas in Communications, 2013, 31(16):2669-2675.

[9] LEE J. A new DC-free multimode code design with error correction capability for optical storage systems[J]. IEEE Transactions on Consumer Electronics, 2010, 56(3):936-948.

[10] SONG J H,MO L,LEE Y H. Holography optical memory recorded with error correcting bits[J]. Journal of Optics, 2014, 16(6):97-107.

[11] JEONGSEOK H, STEVEN W. Low-density parity-check codes over Gaussian channels with erasures[J]. IEEE Transaction on Information Theory, 2003, 49(7):1801-1809.

[12] TAN W J, CRUZ J R. Analyzing low-density parity-check codes on partial response channels with erasures using density evolution[J].IEEE Transactions on Magnetics, 2004, 40(5): 3411-3418.

[13] 李森, 王洁, 马林华. 基于粒子群算法的非规则LDPC码度序列设计[J]. 系统工程与电子技术, 2010,32(6):1151-1154.LI S, WANG J, MA L H. Design of degree sequence for irregular LDPC codes on PSO[J]. Systems Engineering and Electronics, 2010,32(6): 1151-1154.

[14] 孙艺, 王晓凯, 郭大波, 等. 基于粒子群的数据协调优化算法[J].测量技术学报, 2015, 29(2):149-157.SUN Y, WANG X K, GUO D B, et al. The optimized algorithm for data reconciliation based on particle swarm optimization[J]. Journal of Test and Measurement Technology, 2015, 29(2):149-157.

[15] LAN L, ZENG L Q, TAI Y. Construction of quasi-cyclic LDPC codes for AWGN and binary erasure channels: a finite field approach[J].IEEE Transactions on Information Theory, 2007, 53(7):2429-2458.

[16] PRADHAN A, THANGARAJ A, SUBRAMANIAN A. Construction of near-capacity protograph LDPC code sequences with block-error thresholds[J]. IEEE Transactions on Communications, 2015, 11(7):1417-1428.

Analysis of stability condition for LDPC codes and optimizing degree sequences over mixed channel

SUN Kang-ning1, MA Lin-hua1,2, RU Le1, FAN Wen-tong3, HU Xing1, HUANG Shao-cheng1
（1. Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi'an 710038, China;2. State Key Laboratory of Integrated Services Networks, Xidian University, Xi'an 710071, China;3. PLA 94626 Troops, Fuzhou 350002, China）

Under the circumstance that white Gaussian noise and random erasures exist all at once, the stability condition for LDPC codes over mixed channel was proposed. And it was proved that a good degree sequence of LDPC codes was not optimized over mixed channel. It can also be proved by simulation. The random particle swarm optimization (RPSO)and simulated annealing (SA) algorithm were combined to find some capacity-approaching degree sequences over mixed channel with different erasure probabilities. The threshold of signal-to-noise ratio improves 1.615 9 dB than that of the classical degree sequences calculated by Gaussian approximation over mixed channel. These degree sequences are optimal for optical recording and frequency-hopping communication with narrow-band interference.

low density parity check codes, mixed channel, Gaussian approximation, random particle swarm optimization (RPSO), simulated annealing

s: The National Natural Science Foundation of China (No.61472442), Open Foundation of the State Key Laboratory of Integrated Services Networks, Xidian University (No.INS-15-13), Aviation Science Foundation (No.20155896025)

TN911.22

10.11959/j.issn.1000-436x.2016188

2015-08-24；

2016-01-03

国家自然科学基金资助项目（No.61472442）；综合业务网国家重点实验室（西安电子科技大学）开放研究基金资助项目（No.INS-15-13）；航空科学基金资助项目（No.20155896025）