多尺度量子谐振子优化算法的并行性研究

2016-11-24黄焱王鹏程琨刘峰

通信学报 2016年9期

黄焱，王鹏，程琨，刘峰

(1. 淮阴师范学院计算机科学与技术学院，江苏淮安 223300；2. 西南民族大学计算机科学与技术学院，四川成都 610225；3. 中国科学院成都计算机应用研究所，四川成都 610041；4. 成都信息工程大学并行计算实验室，四川成都 610225)

多尺度量子谐振子优化算法的并行性研究

黄焱1，王鹏2，程琨3，刘峰4

多尺度量子谐振子优化算法(MQHOA, multi-scale quantum harmonic oscillator algorithm)是一种利用量子谐振子波函数构造的新的智能算法，采样运算是MQHOA算法的基本运算单元和主要运算量，采样运算的独立性赋予MQHOA算法内在并行性。通过对MQHOA算法群体参数和采样参数进行实验，确定算法的并行粒度并提出多尺度量子谐振子并行算法（MQHOA-P, multi-scale quantum harmonic oscillator parallel algorithm）。在由10个计算节点构成的集群上对6种标准测试函数进行实验，通过改变计算节点数、函数维数和采样参数测试MQHOA-P算法的加速比，实验结果表明，MQHOA-P算法具有良好的加速比和扩展性，可以在大规模集群中部署、运行。

多尺度量子谐振子优化算法；算法并行性；加速比；并行粒度；函数优化

1 引言

MQHOA算法的基本思想是利用函数优化问题与量子谐振子从高能态向基态收敛过程的相似性，结合高斯二进信息采样方法，将函数优化问题的求解过程分为量子谐振子（QHO, quantum harmonic oscillator）收敛和多尺度收敛（M 收敛）2个互相嵌套的收敛过程，通过QHO收敛实现在当前尺度对搜索空间的逐步收缩定位，通过M收敛逐渐提高搜索精度，使目标函数在指定精度找到全局最优解[1]。

MQHOA算法在求解函数优化[2]、组合优化[3]等问题时具有良好的性能，并可以求解聚类中心点[4]等应用问题。文献[1]介绍了 MQHOA算法的基础模型，并对算法的收敛性进行研究；文献[5]通过研究 MQHOA算法与经典谐振子和量子谐振子物理模型之间的对应关系对 MQHOA算法的物理模型进行分析，介绍MQHOA算法中的量子隧道效应和测不准原理；文献[6]将 MQHOA算法用于求解整数非线性规划问题，与QPSO算法进行对比，验证MQHOA算法的性能；文献[7]通过将聚类数据集投影到基于划分的网格，将聚类中心点问题转化为离散函数优化问题进行求解，使用MQHOA算法可以准确地找到聚类中心点位置，并且聚类数据集越大，找到的采样中心点位置越准确，文献[8]提出了具有能级稳定过程的MQHOA算法。

采样运算是MQHOA算法的基本运算单元，其运算量是MQHOA算法主要的运算量。采样运算的独立性赋予MQHOA算法内在的并行性。当求解高维函数优化问题时，随着函数维数的增加，函数解空间呈指数级增加，求解目标函数最优解所需的迭代次数也大幅增长，利用MQHOA算法的并行性可以有效地降低算法的运行时间。

本文通过对 MQHOA算法的采样参数和群体参数进行实验分析，分析MQHOA算法的3种并行粒度，提出MQHOA-P算法，该算法的核心思想是每次迭代运算时主节点将本次迭代的采样中心点和当前尺度发送到从节点，从节点以接收到的采样中心点位置和尺度进行采样运算并在从节点内更新最优解位置，然后各从节点向主节点发起通信，将更新后的最优解位置汇总到主节点，完成一次迭代运算。通过对6种测试函数在不同的函数维数、运行节点数的实验分析，MQHOA算法具有较强的并行性和扩展性。

2 MQHOA算法流程与运行时间

2.1 MQHOA算法流程

MQHOA算法的基本流程如图1所示。

1) 初始化：初始化群体参数k、采样参数m、采样范围S、初始尺度σ0和最小尺度σmin，并在采样范围内随机生成k个初始采样位置算法运行过程中将不断地更新这些采样位置，保留k个最优解。

2) 迭代运算：假设当前为第p次迭代，尺度为σj，k个当前最优解位置为以每个采样位置为中心，分别按照高斯分布生成m个新的采样位置，将km个新采样位置的目标函数值分别与当前的k个最优解位置的目标函数值进行比较，如果出现更优解则替换原采样位置，以上操作为一次迭代运算，完成本次迭代运算后的最优解位置记为

图1 MQHOA算法流程

以一个采样位置为中心根据采样参数和当前尺度生成m个新的高斯采样位置并对目标函数值进行比较是一次采样运算。采样运算是MQHOA算法的基本运算单元。采样运算仅取决于采样位置和当前尺度，采样运算之间没有任何关联关系，采样运算的独立性是MQHOA算法并行性的基础。

5) 输出结果：将当前k个采样位置中的最优位置和目标函数值作为结果输出。

2.2 MQHOA算法的运行时间分析

根据如图1所示的MQHOA算法流程，可将算法划分为初始化、迭代运算、尺度判断、尺度收缩、精度判断和结果输出6个部分，其编号、名称、单位运行时间和运算次数如表1所示。其中，A1、A3、A4、A5、A6的单位运行时间为常数，A2的单位运行时间由算法的群体参数k和采样参数m决定；A1、A4、A5、A6的运算次数为常数，A2、A3的运算次数为算法的迭代次数a1。

每次迭代运算A2包含k次独立的采样运算B1，每次采样运算B1包含m次独立的单位采样B2，单位采样的单位运行时间为D2，由此可得A2的单位运行时间为。

表1 MQHOA算法的运行时间

MQHOA算法的总运行时间为

迭代运算占总运行时间的比例为

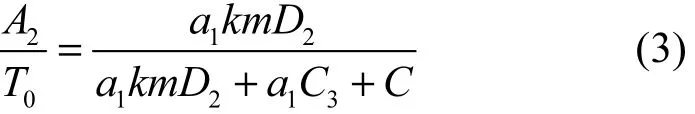
MQHOA算法运行时间由算法迭代次数a1、群体参数k和采样参数m共同决定。MQHOA算法的迭代次数取决于目标函数的复杂程度，随着目标函数维度的增加，函数解空间的数量呈指数级增长，算法的迭代次数a1显著增长，为了快速、准确地获取全局最优解需要加大k和m的数值，采样参数的运行时间会相应地增加，由式(3)可知，迭代运算的占比增大，因此迭代运算是MQHOA算法最主要的运行时间。

3 MQHOA算法的并行化特性

3.1 MQHOA算法的并行方法

算法的并行方法取决于算法逻辑单元之间的依赖关系以及可并行化单元的内部结构[9]。对于MQHOA算法而言，其迭代运算单元间的串行依赖关系和互相独立的采样运算单元的可并行特性决定了算法的并行方法。

设当前迭代为 MQHOA算法的第p次迭代，第p+1次迭代运算的采样中心点位置是第p次迭代运算更新的最优解位置；第p+1次迭代运算的高斯采样尺度取决于σp+1与σs的比较结果，如果，则采样尺度减半，否则采样尺度不变；算法是否执行完毕取决于σp+1与的比较结果，如果则算法终止运行。因此下一次迭代运算的采样中心位置、采样尺度和是否继续迭代均取决于当前迭代运算的结果，MQHOA算法的迭代运算必须串行执行。

MQHOA算法的一次迭代运算包含k次采样运算，在每个采样中心点位置以当前尺度生成m个新解位置，并与当前最优解位置进行比较，采样运算之间互相独立，可以在多个计算节点上并行运行。

MQHOA算法的运行过程是由迭代运算的串行运行构成，由于迭代运算是MQHOA算法的主要运算量，其内含的采样运算是可并行化的，可以通过将采样中心位置发送到多个并行计算节点，使采样运算并行运行，实现MQHOA算法的并行化。根据算法结构确定并行粒度是 MQHOA算法并行化的核心。

3.2 MQHOA算法的3种并行粒度

设MQHOA算法运行在由一个主节点和n个从节点构成的并行计算集群上。划分到从节点运行的任务规模是MQHOA算法的并行粒度，直接影响算法的并行性和并行开销。根据图1所示的MQHOA算法流程，MQHOA算法在迭代运算、尺度判断和精度判断时需要将上次迭代运算的结果进行汇总，因此MQHOA算法有以下3种并行粒度。

1) 粒度1

当MQHOA算法按照粒度1进行并行化时，从节点仅完成本次迭代的并行运算，其并行化框架如图2所示。

图2 采用并行粒度1的并行化框架

与串行程序相比，这种方法将一次迭代运算分发到多个从节点并行计算，其采样中心点的生成方式、数量和收敛条件与串行程序完全相同。将采样中心点位置均分并按照粒度1进行并行化后，每个从节点的运算量是相同的，当从节点的计算性能相同时，每次迭代从节点的运行时间相等。

2) 粒度2

当MQHOA算法按照粒度2进行并行化时，从节点完成当前尺度的并行运算，其并行化框架如图3所示。与串行程序相比，这种方法在当前尺度收敛时使用的采样中心点数量较少，导致当前尺度收敛的迭代次数增加、当前尺度正确收敛的概率降低，大幅增加算法的运行时间，降低获取全局最优解的概率。由于从节点独立完成当前尺度的收敛，每个从节点的迭代运算次数不确定，导致各个从节点的运算时间存在差异，MQHOA算法的并行化时间由运算时间最长的节点决定。

3) 粒度3

当MQHOA算法按照粒度3进行并行化时，从节点完成所有尺度的并行运算，其并行化框架如图4所示。与串行程序相比，这种方法将采样中心点分发到多个从节点独立运行MQHOA算法，运行完后对结果进行汇总，因此同样会增加从节点的迭代次数并降低获取全局最优解的概率。从节点独立地完成所有尺度的收敛的运算时间存在差异，MQHOA算法并行化的时间由运算时间最长的节点决定。

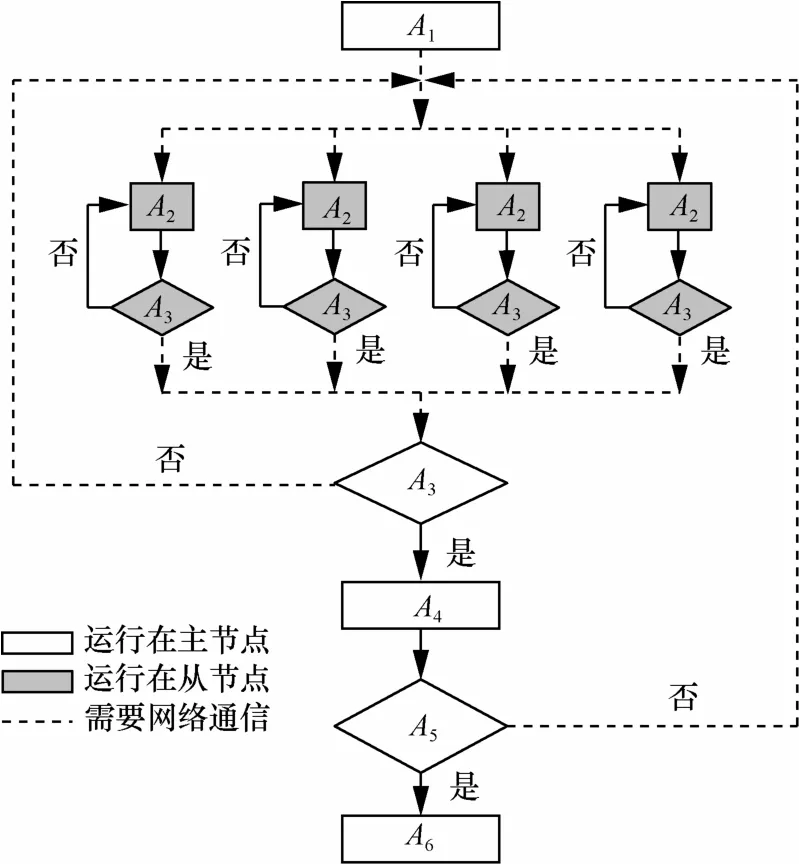
图3 采用并行粒度2的并行化框架

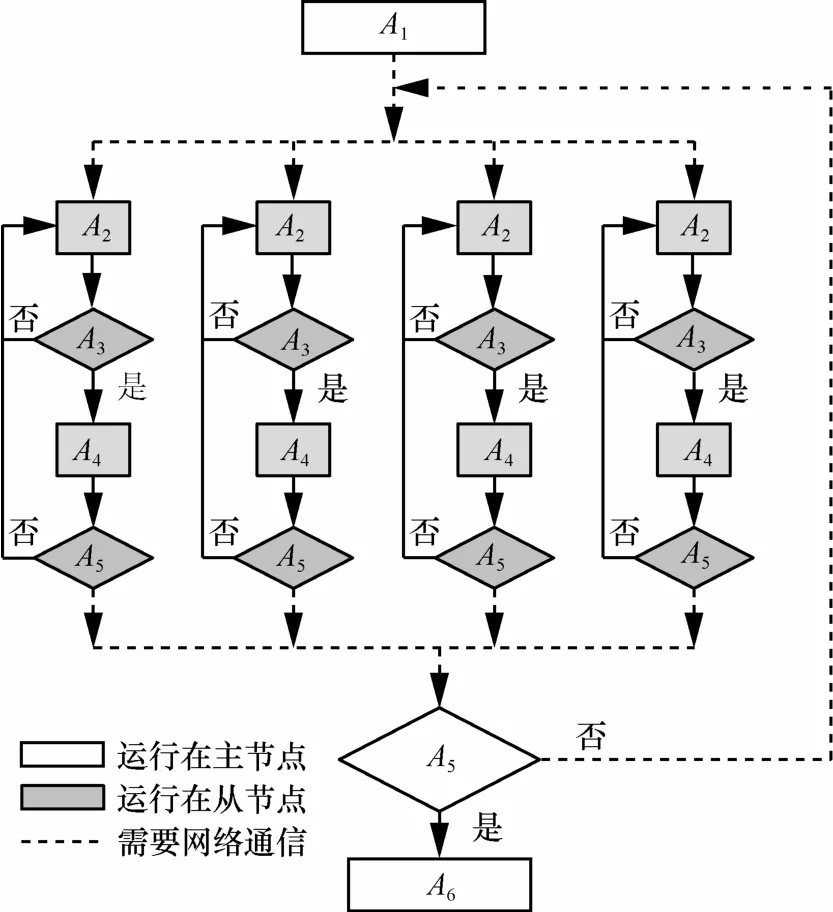
图4 采用并行粒度3的并行化框架

3.3 根据采样参数选择MQHOA算法的并行粒度

采用粒度2和粒度3将采样中心分发到从节点独立地进行迭代运算，与采用粒度1进行并行化相比，每个从节点上运行的采样中心点数较少。MQHOA算法在不同采样参数k下的性能决定了算法并行粒度的选择方法。

将MQHOA算法的参数m依次取10、20、30、40、50、60、70、80、90、100、150、200、250、300、500，参数k依次取10、20、30、40、50、60、70、200、500、1 000，形成150个实验组合，对3维的 Griewank函数在的解空间进行实验，每个实验组合分别进行 10次重复实验，测试算法迭代次数如文献[1]中表1所示。

可以看出，当采用粒度2、粒度3进行算法并行化时，从节点上的采样中心数为串行程序的群体参数k较小，MQHOA算法落入局部最优区域的概率加大，算法求解的准确性下降；与此同时，从节点上的迭代次数大幅增加，算法运行时间大幅增加。因此，本文采用粒度1对MQHOA算法进行并行化研究。

4 MQHOA-P算法的运行流程

根据MQHOA算法流程和算法并行性分析，本节使用粒度 1对 MQHOA算法进行并行化，提出MQHOA-P算法，算法的并行化框架如图2所示，其并行化流程的详细说明如下。

1) 初始化：在主节点完成参数k、m、S、σ0、的初始化运算，在采样范围内随机生成k个初始采样位置，将当前的采样位置平均分为n份，分别发送到n个从节点。

2) 迭代运算：每个从节点按照主节点发送的采样位置和当前尺度进行迭代运算，将更新后的当前最优解位置发送到主节点。

3) 主节点将从节点发送来的k个采样位置进行汇总，计算其标准差σp+1，与算法当前的尺度σs进行比较。如果，则说明当前采样中心点尚未在当前尺度收敛，返回步骤2)继续在从节点上进行迭代运算；如果，则算法已在当前尺度收敛，进行M收敛过程。

5) 输出结果：主节点将当前k个采样位置中的最优位置和目标函数值作为结果输出。

5 MQHOA-P算法的并行化性能分析

MQHOA-P算法的初始化、尺度判断、尺度收缩、精度判断和输出结果均在主节点运行，从节点仅执行迭代运算，算法的收敛条件与串行程序完全相同。

MQHOA-P算法的主从节点间的通信包含3个部分。

1) 算法初始化后主节点向从节点发起一次通信，将初始采样点和算法参数发送到从节点。

2) 从节点完成采样运算后向主节点发起一次通信，将更新后的最优解位置发送到主节点，共进行a1次通信。

3) 主节点接收到从节点发送来的最优解位置后向从节点发起通信，将下一次迭代的尺度发送至从节点，共进行a1−1次通信。

MQHOA-P算法的运行时间为

通信时间占比为

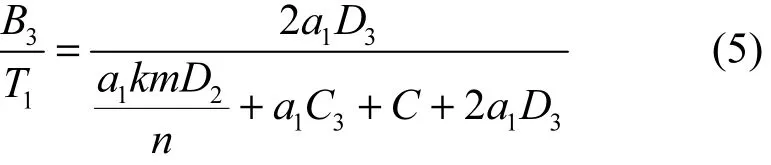
MQHOA-P算法的加速比为

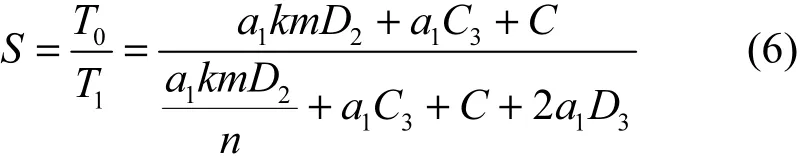
当从节点数增加时，加速度比增加，最大加速比为

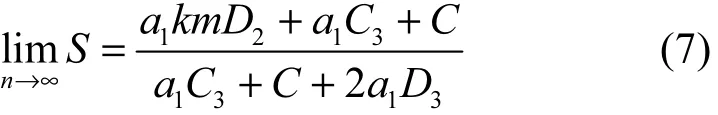
由于迭代运算是 MQHOA-P算法的主要运算量，当迭代次数a1不断增长时，加速比不断增加并趋于稳定。

6 MQHOA-P算法的实验验证

6.1 实验环境

本文在由同构计算节点构成的并行计算集群中进行实验，所有节点的配置为 i3-3220(3.3 GHz)的CPU，4 GB内存，操作系统为CentOS 6.5，将MPICH 3.1.3部署在集群中构建并行计算环境。

6.2 测试函数

本文采用6个典型的高维测试函数对MQHOA-P算法的并行性进行实验分析，测试函数的函数表达式、定义域、最优解位置和全局最小值如表2所示。

表2 测试函数

为了测试MQHOA-P算法的加速比，首先使用MQHOA算法在单机环境中求解6个测试函数的全局最优解，k=80，m=200，函数维数为6，每个测试函数重复 30次实验计算单机平均执行时间，实验数据如表2的最右列所示。

6.3 MQHOA-P算法加速比实验

1) 计算节点数对 MQHOA-P算法加速比的影响

并行算法包含可并行化和不可并行化2种成分的运算量，并行化后的MQHOA-P算法将可并行化部分分别发送到各个子节点运行，子节点仍需运行一部分不可并行化的运算量。

将计算节点数由 2个增加到 10个，使用MQHOA-P算法求解测试函数的全局最优解，，每个测试函数重复30次实验计算平均运算时间，与表2中的单机执行时间进行比较，计算加速比，实验结果如表3所示。从表3可以看出随着计算节点数的增加，MQHOA-P算法加速比首先出现增加趋势，然后逐渐趋于稳定。这个变化趋势与MQHOA-P算法的加速比表达式（6）相符合。由于目标函数的平均迭代次数不同，各目标函数加速比的稳定值存在一定的差异。

2) 函数维数对MQHOA-P算法加速比的影响

随着测试函数维数的增长，函数解空间的数量呈指数级增长，算法迭代运算的次数也不断增长。在由1个主节点和4个计算节点构成的并行计算集群上使用 MQHOA-P算法求解测试函数的全局最优解，函数维数由3维逐渐增加到15维，每个测试函数重复 30次实验计算平均运算时间，求解算法加速比，实验数据如表4所示。从表4可以看出，随着函数维数的增长，算法加速比逐渐增长。这是因为随着函数维数的增长，算法迭代次数不断增加，算法可并行化部分的运算量比例增加，使算法加速比出现增长。

表3 计算节点数对MQHOA-P算法加速比的影响

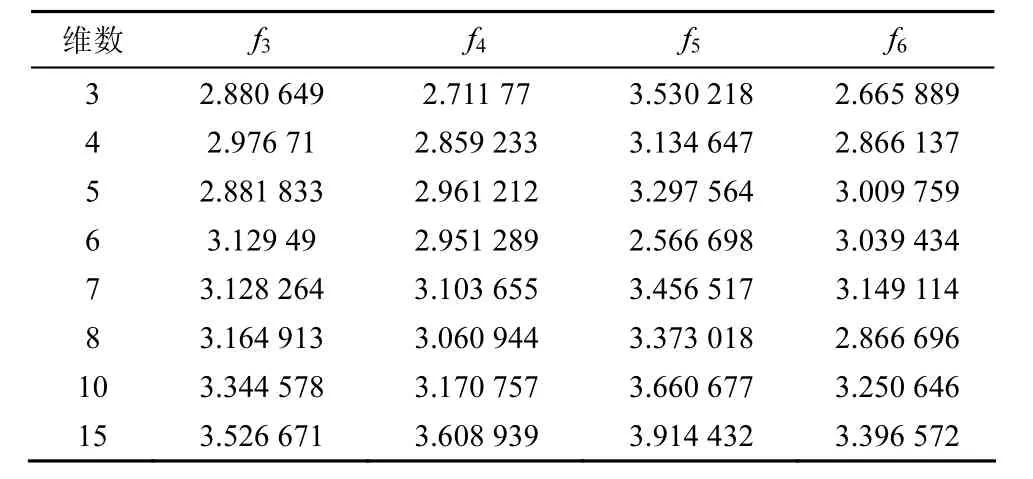
表4 函数维数对MQHOA-P算法加速比的影响

3) 采样参数m对 MQHOA-P算法加速比的影响

采样运算是算法最基本的运算单元，采样运算单元的运算量取决于参数m。参数k依次取 80、100、150、200、250、300，参数m 依次取 200、300、400、500、600，形成30个实验组合，在5个计算节点对6维函数f5进行实验，测试算法加速比，每个组合重复30次实验，实验数据如表5所示。从表5可以看出，随着参数m的增长，算法加速比逐步增长，这反映出随着采样参数m的增长，采样运算单元的运算量相应地增长，算法可并行化部分的运算量比例增加，算法加速比增长。

表5 参数m对MQHOA-P算法加速比的影响

7 结束语

本文通过对群体参数和采样参数进行实验分析确定 MQHOA算法的并行粒度，提出并行化的MQHOA-P算法。通过在10个计算节点构成的集群上对6种标准测试函数进行实验，测试了计算节点数、函数维数和采样参数与算法加速比的关系，实验结果表明，MQHOA算法具有很好的加速比和可扩展性，适用于求解高维函数优化问题。

[1] 王鹏, 黄焱, 任超, 等. 多尺度量子谐振子高维函数全局优化算法[J]. 电子学报,2013,41(12): 2468-2473.WANG P, HUANG Y, REN C, et al. Multi-scale quantum harmonic oscillator for high-dimensional function global optimization algorithm[J]. Acta Electronica Sinica, 2013, 41(12): 2468-2473.

[2] ZABARAS N, YANG G Z. A functional optimization formulation and implementation of an inverse natural convection problem[J]. Computer Methods in Applied Mechanics and Engineering, 1997, 144(3):245-274.

[3] PAPADIMITRIOU C H, STEIGLITZ K. Combinatorial optimization:algorithms and complexity[M]. Courier Corporation, 1998.

[4] LAI J Z C, HUANG T J, LIAW Y C. A fast k-means clustering algorithm using cluster center displacement[J]. Pattern Recognition, 2009,42(11): 2551-2556.

[5] 王鹏, 黄焱. 多尺度量子谐振子优化算法物理模型[J]. 计算机研究与探索, 2015, 9(10): 1271-1280.WANG P, HUANG Y. Physical model of multi-scale quantum harmonic oscillator optimization algorithm[J]. Journal of Frontiers of Computer Science amp; Technology, 2015, 9(10): 1271-1280.

[6] 袁亚男,王鹏,刘峰.多尺度量子谐振子算法性能分析[J]. 计算机应用,2015,35(6):1600-1604.YUAN Y N, WANG P, LIU F. Performance analysis of multi-scale quantum harmonic oscillator algorithm[J]. Journal of Computer Applications, 2015,35(6):1600-1604.

[7] 燕京京.基于量子谐振子模型的聚类中心选取算法[D]. 成都: 中国科学院成都计算机应用研究所, 2015.YAN J J. Clustering center selecting algorithm based on quantum harmonic oscillator model[D]. Chengdu: Chengdu Institute of Computer Application, 2015.

[8] 王鹏,黄焱.具有能级稳定过程的 MQHOA 优化算法[J]. 通信学报,2016,37(7):79-86.WANG P, HUANG Y. MQHOA algorithm with energy level stabilizing process[J]. Journal on Communications,2016,37(7):79-86.

[9] GRAMA A, GUPTA A, KARYPIS G. Introduction to parallel computing: design and analysis of algorithms[M]. Redwood City, CA:Benjamin/Cummings Publishing Company, 1994.

Parallelism of multi-scale quantum harmonic oscillator algorithm

HUANG Yan1, WANG Peng2, CHENG Kun3, LIU Feng4
(1. School of Computer Science and Technology, Huaiyin Normal University, Huaian 223300, China;2. School of Computer Science and Technology, Southwest University for Nationalities, Chengdu 610225, China;3. Chengdu Institute of Computer Application, Chinese Academy of Sciences, Chengdu 610041, China;4. Parallel Computing Lab, Chengdu University of Information Technology, Chengdu 610225, China)

MQHOA was a novel intelligent algorithm constructed by quantum harmonic oscillator's wave function. Sampling was the basic operation and main computational burden of MQHOA. The independence of sampling operation constructs MAHOA’s parallelism. Parallel granularity was obtained by experiments of group parameter and sampling parameter, and MQHOA-P was proposed. Experiments were done in a cluster of ten nodes on six standard test functions. By changing node number, function dimension and sampling parameter, experiments of MQHOA-P’s speed-up ratio were done. The experimental results show the good performance of MQHOA-P’s speed-up ratio and expansibility. MQHOA-P can be deployed and run on multiple nodes in a large-scale cluster.

MQHOA, algorithm parallelization, speedup, parallel granularity, functional optimization

s: The National Natural Science Foundation of China (No.60702075), Sichuan Key Laboratory Open Foundationof Pattern Recognition and Intelligent Information Processing (No.MSSB-2015-9)

TP393

10.11959/j.issn.1000-436x.2016179

2016-01-27；

2016-06-27

王鹏，wp002005@163.com

国家自然科学基金资助项目（No.60702075）；模式识别与智能信息处理四川省高校重点实验室开放基金资助项目（No.MSSB-2015-9）