导管桨水动力性能计算精度影响因素分析

邱 鹏，贺 伟，胡方凡

(1.武汉理工大学 交通学院，湖北 武汉430063；2. 武汉理工大学 高性能舰船技术教育部重点实验室，湖北 武汉430063)



导管桨水动力性能计算精度影响因素分析

邱 鹏1,2，贺 伟1,2，胡方凡1,2

(1.武汉理工大学 交通学院，湖北 武汉430063；2. 武汉理工大学 高性能舰船技术教育部重点实验室，湖北 武汉430063)

为了研究导管桨水动力数值模拟过程中不同因素对其计算精度影响的规律，选择19a导管和ka 4K-70桨作为计算模型，通过求解RANS方程，分别对导管桨在进度系数j=0.3时，不同交接面位置、不同旋转域划分、不同计算外域划分和不同湍流模型的水动力性能进行数值模拟，并与已有实验值进行对比，探究不同因素对其性能计算精度的影响，同时分析了各自的流场特点。研究得出的相应结论，对今后的导管桨水动力性能的数值模拟计算起到一定的参考作用。

导管桨；水动力性能；数值模拟；精度分析

0 引言

导管桨由于其高效的节能推进特性，在当今要求船舶节能的世界中受到越来越多的关注，应用于各大工程类运输船舶推进中。目前，导管桨水动力性能的研究主要采用数值计算和实验方法这2种方法。由于数值研究相对于实验研究具有研究时间短、成本低、简单快捷等优点，因而应用较广泛。数值模拟研究主要有基于势流理论的面元法和基于粘性流理论的求解RANS方程的CFD 方法。在CFD计算研究方面，Abdel等[1]和Bulten[2]对导管桨缩比模型和全尺模型的流场进行了数值计算，并就尺度效应对导管桨敞水性能的影响进行了分析。赵强[3]在其论文中对导管桨计算做了系统的边界条件设置介绍，并与实验值进行了对比，张弘等[4]也利用Fluent软件分析了导管桨不同几何参数对其水动力性能的影响。综观现有的导管桨数值模拟研究，很少有人就其性能计算精度方面做出系统的分析和总结。本文将从导管桨性能计算精度的影响因素方面做出分析，利用Fluent软件进行数值精度研究，并与已有实验值进行比较，对以后的数值模拟计算方面起到一定的借鉴作用。

1 研究对象和模型建立

本文的研究对象采用ka 4-70桨和19a 导管，其螺旋桨的相关重要参数[5]见表1。

表1 螺旋桨基本参数

导管和螺旋桨之间的间隙为1 mm。其导管桨的物理模型在Icem三维建模软件中完成，物理模型如图1所示。下面所有的方案都需计算来流进速V=0.7 m/s，转速N=700 r/min，进度系数j=0.3时的工况。

图1 导管桨三维模型

本文在雷诺平均N-S方程的基础上，采用Fluent软件进行流场计算，求解器选用SIMPLE压力速度耦合方法，湍流模型暂时采用考虑具有旋转效应的RNGk-ε模型，并结合标准壁面函数；选用MRF模型来近似模拟螺旋桨之间的相对旋转运动，旋转域绕桨毂旋转；计算域进口(in)选择速度入口(velocity-inlet)边界条件，计算域出口(out)采用outflow边界条件；耗散系数ε和湍流参数湍动能k采用默认的数值来设定；桨叶、桨毂和导管表面均采用固定壁面(wall)边界条件；外域边界采用滑移壁面(moving wall)边界条件，和来流保持相对静止，设定移动方向和相对静止流体域；考虑到不同流域间速度、温度和能量等参数的信息传递交换，对于不同流域之间的交接面采用interface边界条件；压力离散格式和扩散项的离散均采用二阶精度的中心差分格式，对流项离散采用二阶迎风格式。

2 影响因素分析

2.1 交接面位置的影响分析

螺旋桨由于其复杂的物理模型，采用非结构四面体网格划分，外部静止域先采用非结构网格划分，外域水流入口端面距离桨盘面8D(D为螺旋桨直径)，水流出口端面距离桨盘面10D，圆柱体半径为4D。无论是计算普通的螺旋桨还是导管桨都需要有分为螺旋桨同轴的包裹螺旋桨的旋转域和远场的静止域，计算域如图2所示。在这里先将导管内壁作为旋转域的一部分来封闭旋转域，只考虑旋转域交接面位置不同带来的计算精度影响。在基于CFD的导管桨性能计算的有关研究中，马艳[6]、朱俊飞[7]、赵强[3]等在设置轴向的旋转域与静止域交接面时都没有具体讨论过其交接面与螺旋桨盘面中心的距离，此处所述的交接面就是图3中螺旋桨左右的2个圆形，桨左面的圆记为前交接面，后面的记为后交接面，其中导管长度为100 mm，本文将对4个位置进行具体的讨论。方案1为前后交接面距离中心原点的距离都是35 mm；方案2为前后交接面距中心的距离是45 mm；方案3为前交接面距离中心为35 mm，后交接面为45 mm；方案4为前交接面距离中心为35 mm，后交接面为40 mm。在计算结果中导管推力系数为KTD，螺旋桨推力系数为KTP，总推力系数为KTT，转矩系数为KQP，计算误差=100(计算值-实验值)/实验值。模拟计算的最终计算结果见表2。

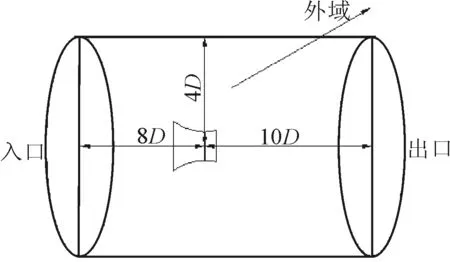
图2 计算域示意图

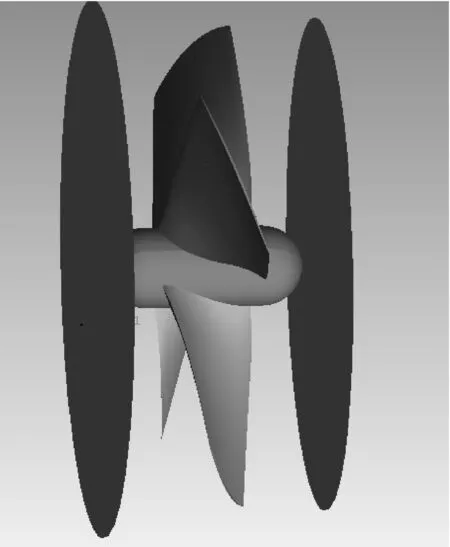
图3 交接面示意图

表2 交接面位置不同导致的计算结果

由计算结果可知，方案1中，当前后交接面离桨都比较近时，导管的计算误差比螺旋桨的要小。方案2中,当交接面距离比较大时，螺旋桨的计算结果比导管桨的要更贴近实验值一些。但是方案4中，导管和螺旋桨的计算结果都比较贴近实验值，也就是前交接面距离桨中心近点，后交接面距离桨中心位置适中时。由此可以提出结论：首先旋转域不宜过长，因为计算中采用的是MRF模型，采用近似旋转的方法来模拟实际的流动，而实际的流动也只有螺旋桨旋转，其余区域流体不旋转，因此旋转域不宜像方案2那样过长；当前交接面距离桨中心比较近，而后交接面距离桨中心适中时，此时的模拟流场与实际实验中比较相符，计算结果比较吻合实验值。

2.2 不同旋转域划分影响分析

上述将导管内壁作为旋转域的一个封闭面,马艳[6]、朱俊飞[7]、赵强[3]等计算导管桨的性能以及范露[8]计算吊舱推进器时也都是做此处理的。本文试图将旋转域仅仅包裹螺旋桨，将导管内壁完全划分在静止域中，旋转域的侧面和导管的内壁相平行，但是其比内壁高度低0.5 mm(将此方案记为方案5)，其中，交接面采用上述方案4中的结论，计算结果见表3。

从表3的数据分析可以看出，采用方案5的旋转域的划分方法与以往的将导管内壁放在旋转域中，其计算误差明显相对减小，特别是螺旋桨的推力系数和转矩系数采用方案5更为精确，误差小于1%。下面将从流场云图来比较两者之间的差距。

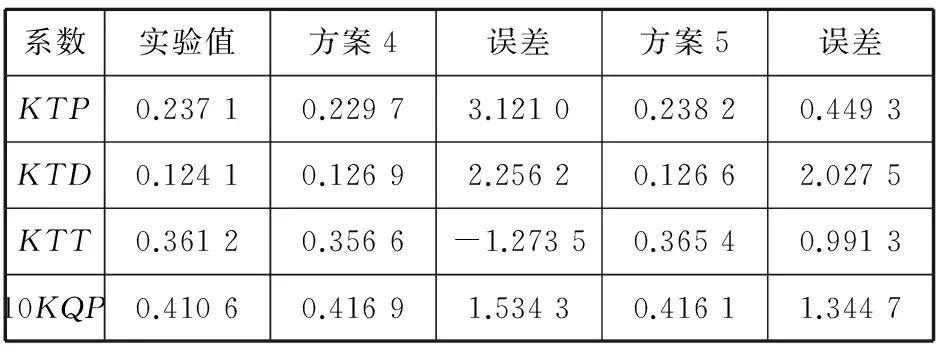
表3 旋转域不同导致的计算结果

从分析图4桨叶压力云图发现，方案5和方案4的叶面压力均大于叶背压力，符合实际中的压力分布情况，形成推力向前。同时发现，由于旋转域的不同，也就是由于在方案5里面，导管内壁和螺旋桨之间有轴向的流动速度，而方案4则没有，其方案5的难度在于网格划分难度比较大，但是与实际流动更符合，这也导致了在图4桨叶压力云图(a)中方案5的叶背压力明显比图4(b)中方案4的压力大，图4(c)中方案5叶面压力也大于图4(d)中方案4的压力，其数值也更接近实验值。导管的推力在数值上相差不大，螺旋桨的转矩误差也是方案5比较小。从图5轴向的速度云图中可以看出,方案5中的导管内壁和桨叶叶梢之间有轴向流动，其内壁附近的速度比方案4中的内壁附近速度要低，导致了桨叶压差有很大不同。

图4 桨叶压力云图

2.3 不同外域划分的影响分析

上述分析了旋转域交接面位置与旋转域划分方法不同而对导管桨性能计算精度的影响，下面讨论外域不同划分对其影响。

采用结构和非结构网格相结合的混合网格方式来划分外域，此方案记为方案6。处理的过程就是加1个中间域来包裹导管，最外面还是和方案5一样大小的静止域，网格数量达到3 321 630，非结构网格(方案5)数量达到3 061 101,但是发现2种计算结果基本没有变化，计算结果见表4。原因在于方案6的网格划分会导致交接面的数量的增多，而交接面存在会导致计算精度的丢失，所以方案6虽然外域部分采用结构化网格，其最终的结果和方案5相差不大。

图5 轴向速度云图

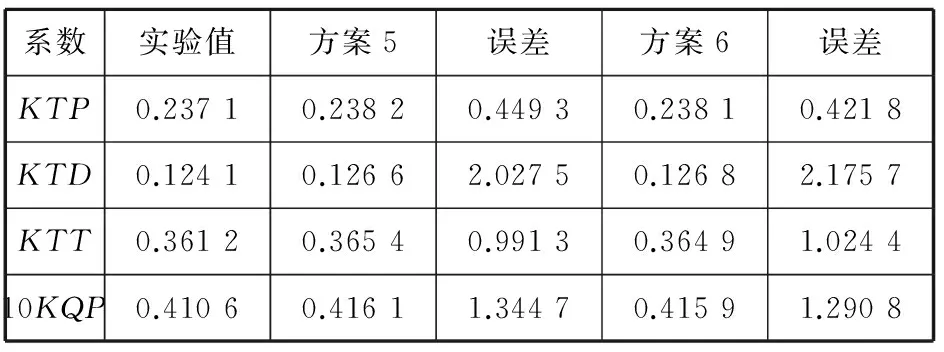
系数实验值方案5误差方案6误差KTP0.23710.23820.44930.23810.4218KTD0.12410.12662.02750.12682.1757KTT0.36120.36540.99130.36491.024410KQP0.41060.41611.34470.41591.2908

2.4 不同湍流模型的影响分析

在方案5的基础上考虑湍流模型的影响，分别选用标准k-ε模型、RNGk-ε模型、SSTk-ε模型，计算结果见表5。

由计算结果可以发现，标准k-ε模型对导管桨性能计算精度影响误差比较大，不太合适19a导管配上桨ka 4-70模型，这是因为标准模型对于较大流线曲率情况不太适用，针对旋转和分离流场这种较大流线曲率的流场，标准k-ε模型不太适用。考虑到流线曲率产生另外的应变，湍流扩散也会进一步加强，因此带有修正项的RNG 模型和SST 模型都可以更好地捕获流场信息。在本例中RNGk-ε模型，SSTk-ε模型更适合数值模拟。

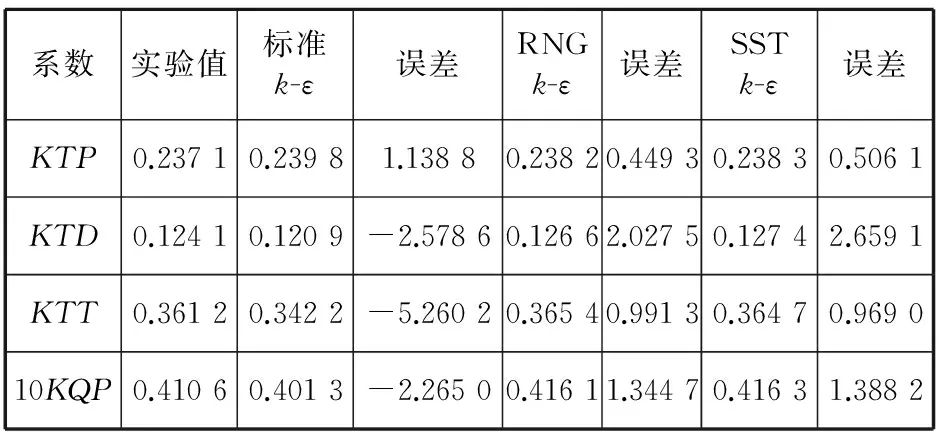
表5 湍流模型不同导致的计算结果

3 结论

随着计算流体力学的发展，采用数值模拟的方法来计算导管桨水动力能已成为一种主流的研究手段。本文采用Fluent商用软件对导管桨水动力性能计算精度进行了分析，在导管桨水动力性能数值模拟过程中得出如下结论：

(1)旋转域轴向方向不宜过长，前交接面位置靠近桨中心，后交接面位置要适中。

(2)只将螺旋桨包裹起来的旋转内域可以更好地模拟实际流场，计算精度最好。

(3)外域网格划分结果基本没影响，RNGk-ε模型，SSTk-ε模型更适合导管桨。

[1] Abdel M M, Heinke H J. Scale effects on ducted propellers[C]//Twenty-Fourth Symposium on Naval Hydrodynamics. Washington: Office of Naval Research, West Japan Society of Naval Architects, National Research Council, 2003.

[2] Bulten W H. Numerical Analysis of Flow Around a Thruster[R]. Houston: Dynamic Positioning committee, 2006.

[3] 赵强. 导管螺旋桨水动力性能和船尾伴流场的CFD模拟[D]. 武汉：武汉理工大学, 2011.

[4] 张弘, 邹义, 王涛,等. 导管参数对导管桨水动力性能的影响研究[J].船舶工程, 2015,37 (S1):71-75.

[5] 梅琴生.船舶螺旋桨简易设计[J]. 江苏船舶, 1989，6(2):38-62.

[6] 马艳. 导管螺旋桨的水动力性能分析与设计优化[D]. 哈尔滨：哈尔滨工程大学, 2010.

[7] 朱俊飞. 导管螺旋桨水动力分析与优化研究[D]. 武汉：武汉理工大学, 2013.

[8] 范露. 吊舱推进器的水动力性能优化设计研究[D]. 武汉：武汉理工大学, 2008.

2016-04-22

国家自然科学基金项目(51409201)与中央高校基本科研业务费专项基金(2015IVA029)资助

邱鹏(1990—)，男，硕士研究生，研究方向为船舶水动力性能；贺伟 (1982—), 男，博士，讲师，研究方向为船舶水动力性能。

U661.31+3

A