Variational Bayesian labeled multi-Bernoulli filter with unknown sensor noise statistics

Qiu Hao,Huang Gaoming,Gao Jun

College of Electronic Engineering,Naval University of Engineering,Wuhan 430033,China

Variational Bayesian labeled multi-Bernoulli filter with unknown sensor noise statistics

Qiu Hao*,Huang Gaoming,Gao Jun

College of Electronic Engineering,Naval University of Engineering,Wuhan 430033,China

It is difficult to build accurate model for measurement noise covariance in complex backgrounds.For the scenarios of unknown sensor noise variances,an adaptive multi-target tracking algorithm based on labeled random finite set and variational Bayesian (VB) approximation is proposed.The variational approximation technique is introduced to the labeled multi-Bernoulli (LMB) filter to jointly estimate the states of targets and sensor noise variances.Simulation results show that the proposed method can give unbiased estimation of cardinality and has better performance than the VB probability hypo the sis density (VB-PHD) filter and the VB cardinality balanced multi-target multi-Bernoulli (VB-CBMeMBer) filter in harsh situations.The simulations also confirm the robustness of the proposed method against the time-varying noise variances.The computational complexity of proposed method is higher than the VB-PHD and VB-CBMeMBer in extreme cases,while the mean execution times of the three methods are close when targets are well separated.

1.Introduction

Random finite set (RFS) theory1,2provides a systematic mathematical foundation for the multi-target tracking (MTT) problem and arises widespread interest in the last decade.Major algorithms include probability hypothesis density(PHD)filter2,cardinalized PHD (CPHD) filter3,4and cardinality balanced multi-target multi-Bernoulli (CBMeMBer) filter.5Strictly,those RFS-based filters are not multi-target tracker because the y assume that the objects are indistinguishable.6For this problem,Ref.7proposed a newly labeled RFS approach,known as the δ-generalized labeled multi-Bernoulli (δ-GLMB) filter.The main advantages of the δ-GLMB filter over traditional RFS filters are that it can output trajectories and has a better performance in harsh environments,such as low detection probability and large sensor noise variances,though with higher computation burden.The labeled multi-Bernoulli (LMB) filter8is proposed to reduce the number of components of δ-GLMB by moment approximation and track grouping strategy.

The standard RFS algorithms mentioned above hold the assumption that the prior knowledge of sensor noise statistics are known,while it is usually difficult to build an accurate model for the sensor noise variances in practice.Multiple model(MM)9and particle filter(PF)10are adaptive Bayesian methods for unknown parameters.However,the y have been computationally expensive since their performances rest on the number of models or particles.Compared to MM and PF methods,variational Bayesian(VB)approximation11,12is more dedicate and efficient in dealing with uncertain sensor noise variances tracking problems within linear Gaussian condition.Yang,13Zhang14and Wu et al.15,16extended the VB method to MTT scenario with the PHD filter,respectively.Adaptive VB methods based on the CBMeMBer filter have been studied17–19as well.Due to the inherent weakness of PHD and CBMeMBer,the VB-PHD and VB-CBMeMBer filters do not perform well in the low signal-to-noise ratio(SNR)situations.To improve this problem,this contribution introduces the VB approach to the LMB filter framework,making it suitable for real world scenarios.The proposed VB-LMB filter inherits the efficiency of VB approximation and the advantages of LMB filter in harsh environments,as well as the higher computational price.

This manuscript is organized as follows.Section 2 briefly discusses the background of the VB approximation and standard LMB filter.The VB-LMB filter and its implementation issues are detailed in Section 3.Section 4 shows the results of the proposed and compared algorithms.Finally,conclusions can be found in Section 5.

2.Background

2.1.VB approximation

The dynamic model of linear Gaussian system is given by

where x is the target state and z the measurement;F and H represent the transition matrix and observation matrix,respectively,v and w are independent zero-mean Gaussian noises with covariance Q and R,respectively.R is supposed to have the form of,whereis the measurement noise variance and d the dimension of measurement.+denotes the next time step.

The goal of the variational approximation is to jointly estimate the target state and measurement noise covariance.Suppose that the joint prior distribution has the factored form of

where N(.)and IG(.)represent the Gaussian and inverse Gamma distributions,respectively.As the assumption that target state and measurement noise covariance are mutually independent,at prediction step,the Gaussian and inverse Gamma distributions in Eq.(3)evolve independently.Thus,the predictive distribution keeps the form of the prior distribution

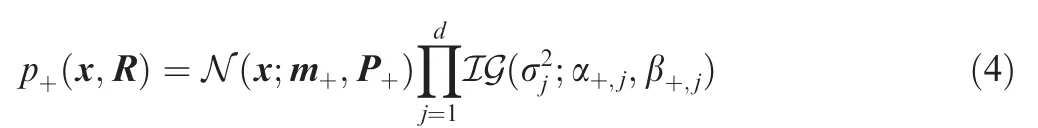
To make the coupled update step tractable,the VB method has been applied to obtaining the posterior distribution

and the Kullback-Leibler(KL)divergence from~p(x,R|z)to p(x,R|z)is given by

The KL divergence will achieve minimum if

The results in Ref.12illustrate that Qx(x)has a Gaussian distribution and QR(R)is a product of inverse Gamma distributions.Consequently,the approximated posterior distribution has the same factored form as the prior distribution.

2.2.Original LMB filter

The traditional RFS-based filters assume that targets are indistinguishable.Recently,Ref.7introduced a labeled model to address the uniqueness of individual target.Let X be a finite set that represents the multi-target state and the labeled RFS is described as

where x and l∈L are the state and label of a single target,respectively,and L is the label space;M is the number of targets.Let the notation Δ(X)= δ|X|(|L(X)|)be the distinct label indicator,where L(X)denotes the labels set of X;|.|indicates the cardinality of a set.

An important form of multi-target density called d-GLMB RFS is introduced,also known as Vo-Vo density7

where each I∈F(L)represents a hypothesis with a set of track labels,and F(L)is a subset collection of space L;ω(I)is the weight of hypothesis I and∑denotes the spatial distribution of target;the unlabeled multi-target exponential function is defined as[p]X=1 when X=Ø and when∏

The δ-GLMB RFS is a conjugate prior of the Chapman-Kolmogorov equation and Bayes multi-target inference,which facilitates a close form implementation of the multi-target Bayesian filter.The optimal solution to the δ-GLMB filter is intractable since the number of components grows exponentially.The LMB filter is an approximated version of the δ-GLMB filter.This section outlines the prediction and update of the LMB method,and the full details can be found in Ref.8.

Suppose that the prior multi-target density can be described as LMB density

where r(l)and p(l)(x)are the existence probability and the spatial distribution of a target,respectively.Assume that the density of new birth is,where B is the label space of birth and L∩B= Ø,the n the LMB predictive density π+(X)is given by

where

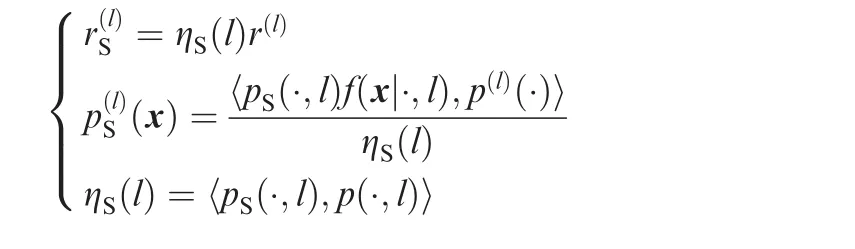
and wheref(x|.,l)is the state transition function;pS(.,l)is the survival probability.

Let Z denotes theset of measurements,and the predictive density iswhere L+=L ∪ B.The LMB posterior density iswhere

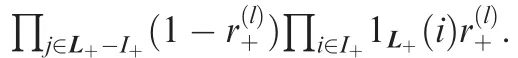
3.Proposed method

3.1.VB-LMB filter

To obtain the VB-LMB filter,the labeled RFS should be extended to a hybrid state space

where the target state x and covariance R are statistically independent.The VB-LMB method can be obtained straightly by substituting the hybrid state into the original LMB filter.Assume that the prior density is an LMBRFS with hybridstate:π(X)={r(l),p(l)(x,R)}l∈L.The predictive density is given by

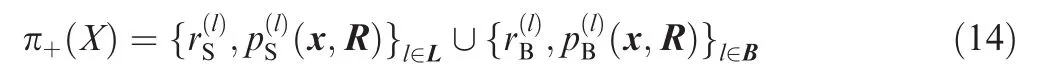
where

Rewrite the predictive density as(x,R)}l∈L+;based on the original method,the multi-target posterior density is given by

where

3.2.A closed form implementation

This section details a closed form solution to the VB-LMB filter with mixture of Gaussian and inverse Gamma distributions.The survival and detection probabilities are assumed to be independent with the target state:pS(x,R,l)=pS,pD(x,R,l)=pD.

3.2.1.Prediction

Supposed that the prior multi-target density is an LMB RFS and the spatial distribution of each target is a Gaussian and inverse Gamma mixture of the form

the predictive density described in Eq.(14)can be calculated as

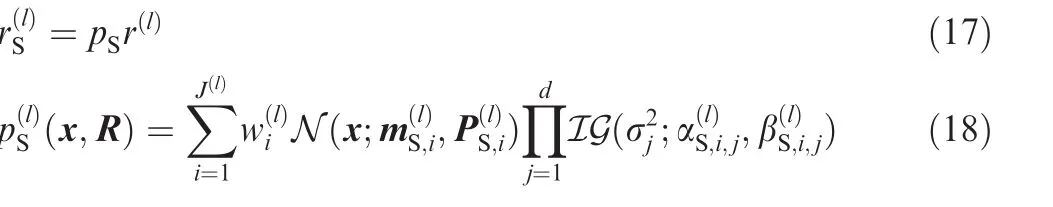
where

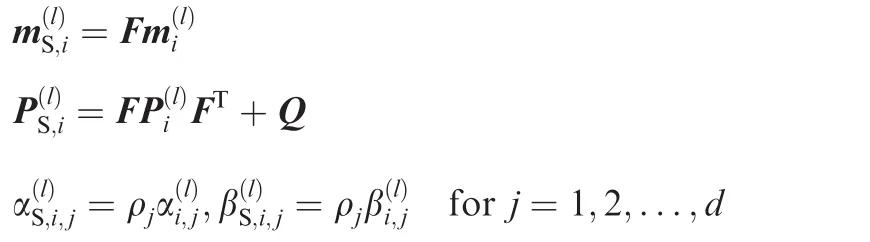
and where ρj∈ (0,1]denotes the factor to accommodate the time-fluctuations of variance.The spatial distribution of spontaneous birth is given by

3.2.2.Update

The predictive density can be reorganized as the sameform as the prior density.Suppose that the spatial distribution of the predictive density is given by

As described in Eq.(15),the posterior multi-target densityconsists of a number of hypothetical distributions.For each hypo the sis(I+,ε),the update distribution is entirely characterized by ω(I+;ε)and 1I(l)p(l)(x,R;ε).From Refs.12,13,we know that p(l)(x,R;ε)also has the following form:

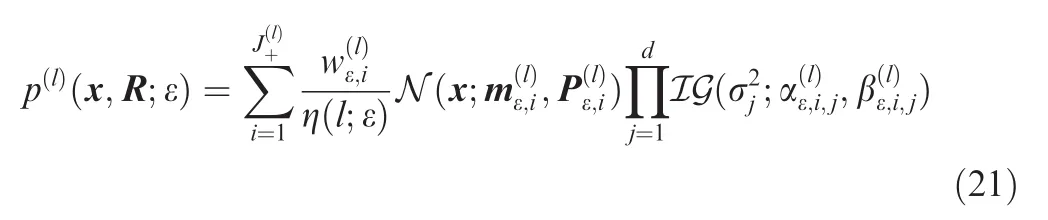
where

For ε(l)=0,namely,object(x,l)is miss-detected,the n Eq.(21)is characterized as

Else if ε(l)gt;0,the variational Bayesian adaptive Kalman update12is employed to approximate the parameters.Firstly,initialfor j=1,2,...,d.Then,iterate the following for N times:for n=1,2,...,N,

In fact,variational approximation method converges very fast with a few iteration steps.Through iteration we getfor j=1,2,...,d;the weight of each new component is given by

4.Simulations

A 2D scenario with surveillance region[-1000,1000]mX[-1000,1000]m is considered.Let x=[x,y,x′,y′]Tbe the target state,where(x,y)and(x′,y′)denote the position and velocity of target,respectively.The dynamics is given by

where I2denotes a 2X2 identity matrix and σv=1 m.The observation model can be described as

where standard deviations σw,1and σw,2are not known to the filter.For simplicity,σw,1and σw,2are assumed to be identical,σw,1= σw,2= σ=5 m.The survival probability is pS=0.98 and the detection probability is pD=0.98.False detections are uniformly distributed over the surveillance region with Poisson cardinality distribution λC=10.

Fig.1 Cardinality statistics for different methods.

The density of spontaneous birth is given by

m the given density are placed in the scene.The appearance and disappearance of targets are not known to the filters;hence,all filters are initialized with zero state.

Targets with existent probability below Tr=10-4are eliminated;the weight and measurement noise variances pruning threshold of a Gaussian-Inverse Gamma component are Tw=10-3and TR=105,respectively.Merging threshold is U=4 and the maximum number of components is Jmax=104.Grouping gate of Bernoulli filters is γ=9.Fading factor of inverse Gamma distributions is ρ=0.9 and the iteration times N=5.

4.1.Experiment 1

In this case,only constant measurement noise variances are considered.The performance of the VB-LMB filter is compared to the standard Gaussian mixture LMB (GM-LMB),VB-PHD and VB-CBMeMBer filters,and the measurement noise variances are only known to the GM-LMB method.

The average cardinality estimates over 100 Monte Carlo trials are plotted in Fig.1.The results show that all of the three adaptive methods can provide unbiased estimation of target number,while the standard deviations of the proposed method are smaller than the VB-PHD and VB-CBMeMBer filters.The dominate reason lies in the fact that the update step of the VBLMB is closed while the VB-PHD only propagates the first moment of multi-target density.The results also suggest that the VB-CBMeMBer performs similarly to the VB-PHD since the computational complexities of the two methods are both liner in the number of measurements.The corresponding OSPA20distances(p=1,c=200 m)shown in Fig.2 confirm the results of Fig.1.Obviously,VB-LMB adjusts more rapidly than the VB-PHD and VB-CBMeMBer filters at the beginning(time step klt;25),and the OSPA distances of the VB-LMB are very close to the original filter in the period of kgt;30.The disadvantage is a delayed response to the disappearances of targets(k=40,45).

Fig.2 Average OSPA distances for different methods.

Fig.3 shows the time averaged OSPA distances with different iteration times.The results illustrate that the variational approximation converges very fast for about 3 iteration steps;as a consequence,the OSPA distances of the three adaptive filters are nearly identical for N≥3.

Fig.3 Time averaged OSPA distances versus iteration times.

Fig.4 Time averaged OSPA distances versus detection probability.

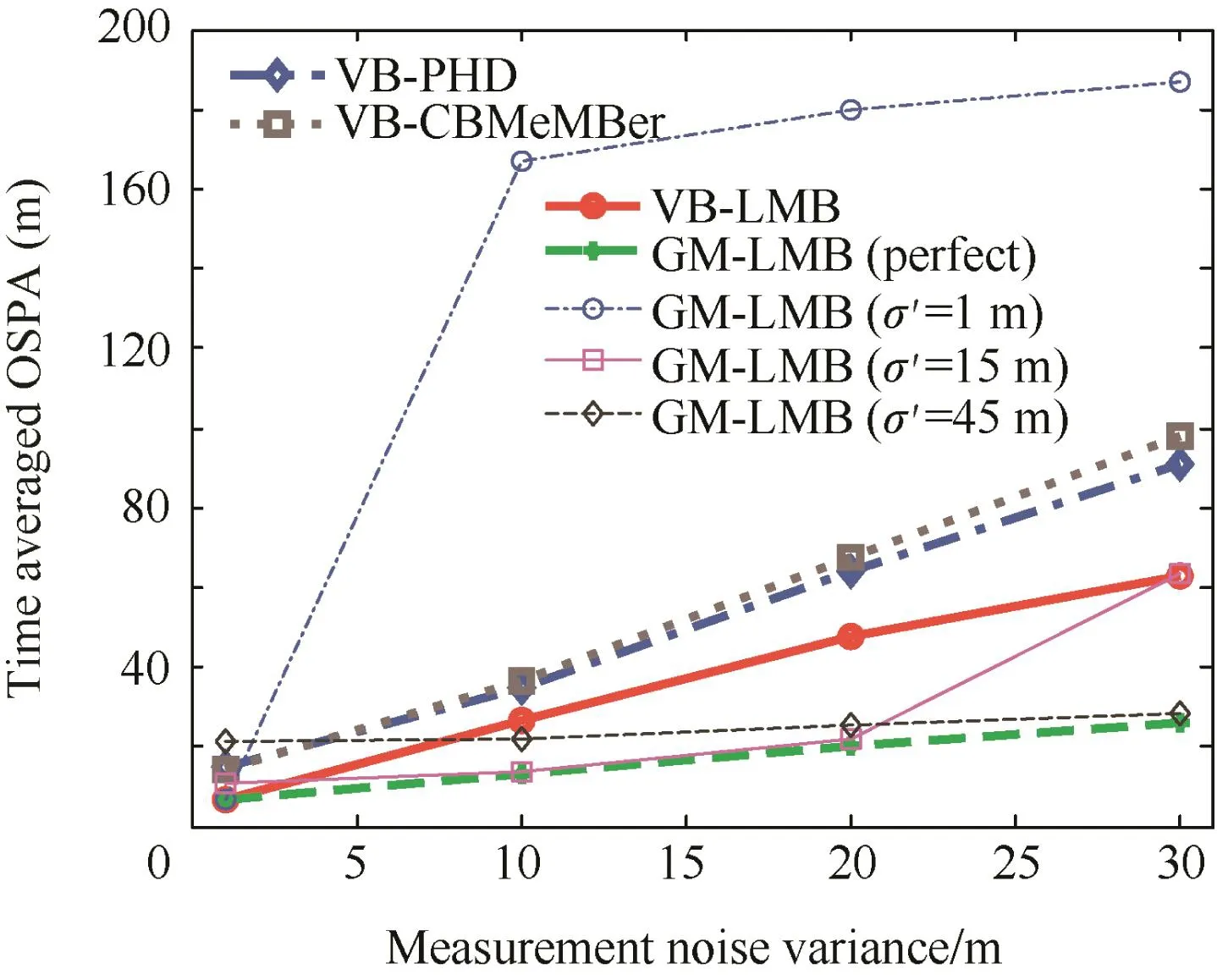
Fig.5 Time averaged OSPA distances versus measurement noise variance.

The time averaged OSPA distances with different PDand σ are plotted in Figs.4 and 5,respectively,where σ′is the measurement noise variance employed by the original filters.Clearly,the proposed method is more stable in the scenarios of low PDor large σ.Like the PHD filter,the VB-PHD filter holds the assumption that the target number has a Poisson distribution which will lead to a high deviation of cardinality estimation.Thus,the VB-PHD filter will be easily influenced by miss-detections or larger noise variances.The CBMeMBerbased filters hold the assumption that pD≈1,thus,the valid performance of the VB-CBMeMBer method is most likely to be with the scenarios of high detection probabilities.On the contrast,the VB-LMB filter inherits the advantage of the LMB filter in harsh environments.In addition,Fig.5 also implies that the standard GM-LMB filter cannot work properly if σ is much smaller than the true model.Generally,the original filter with larger measurement noise variances is more tolerant of the miss-match of the models.

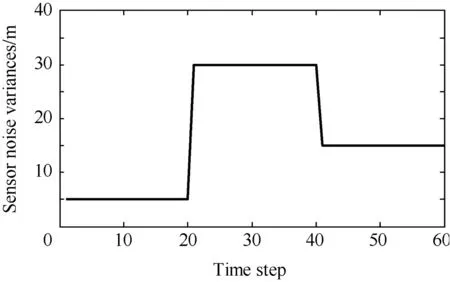
Fig.6 Model of time-varying measurement noise variances.

4.2.Experiment 2

In this scenario,the measurement noise variances are timevarying.The model of σ is plotted in Fig.6.To mitigate the influence of target birth and death,the scenario consists of only four targets from different birth intensities and all targets survive for 60 time steps.

The position estimates of the three adaptive methods are plotted in Fig.7.Both of the VB-PHD and VB-CBMeMBer exhibit signs of cardinality underestimate due to the fluctuations of σ.The Monte Carlo average OSPA distances are shown in Fig.8.It is clear that the proposed method is more robust than the VB-LMB and VB-CBMeMBer in dealing with time-varying noise.The results of the VB-PHD and VBCBMeMBer fluctuate distinctly when σ varies(k=20,40),while during the same period,VB-LMB is nearly identical with the perfect GM-LMB filter.The heuristic measurement-totrack merging scheme employed by the CBMeMBer filter is essentially a single hypo the sis correlation approach,which makes the CBMeMBer-based methods not suitable for harsh scenarios,such as targets are close or measurement noise vari-ances are large.Like the original filters,the computational complexities of the VB-PHD and VB-CBMeMBer are both linear in the number of detections|Z|.On the other hand,the computational complexity of the VB-LMB is O(|Z|3)at worst,where all targets and detections gather so that the grouping strategy loses efficiency.Obviously,it is an extreme scenario,and most of the time the computational complexity of the proposed method is less than O(|Z|3).In this experiment,the mean execution times of the VB-PHD,VB-CBMeMBer and VB-LMB are 0.12,0.11 and 0.14 s,respectively.

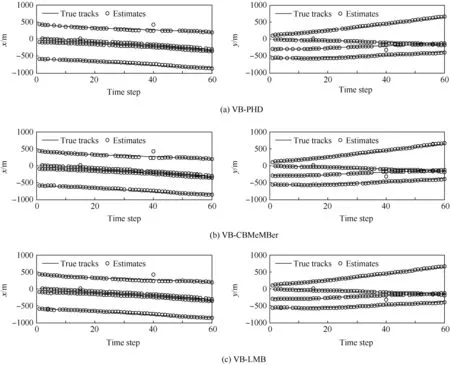
Fig.7 Position estimates of a single trial.

Fig.8 Average OSPA distances for time-varying measurement noise variances.

5.Conclusions

For the scenarios with little prior knowledge of the measurement noise variances,an adaptive MTT algorithm is proposed.To simultaneously estimate the multi-target states and the measurement noise variances,an extended LMB filter is implemented in the variational Bayesian adaptive Kalman filter framework.Experimental results verify the outperformance of the proposed method over the VB-PHD and VBCBMeMBer filters.The computational cost of the VB-LMB filter is slightly higher than the two compared methods when targets are not close.

Acknowledgements

This work was supported by the National High Technology Research and Development Program of China (No.2014AA7014061)and the National Natural Science Foundation of China(No.61501484).

1.Mahler R. Statistical multisource multitarget information fusion.Boston:Artech House;2007.p.343–99.

2.Mahler R.Multitarget Bayes filtering via first-order multitarget moments.IEEE Trans Aerosp Electron Syst 2003;39(4):1152–78.

3.Mahler R.PHD filters of higher order in target number.IEEE Trans Aerosp Electron Syst 2007;43(4):1523–43.

4.Vo BT,Vo BN,Cantoni A.Analytic implementations of the cardinalized probability hypothesis density filter.IEEE Trans Signal Process 2007;55(7):3553–67.

5.Vo BT,Vo BN,Cantoni A.The cardinality balanced multi-target multi-Bernoulli filter and its implementations.IEEE Trans Signal Process 2009;57(2):409–23.

6.Beard M,Vo BT,Vo BN.Bayesian multi-target tracking with merged measurements using labeled random finite sets.IEEE Trans Signal Process 2015;63(6):1433–47.

7.Vo BT,Vo BN.Labeled random finite sets and multi-object conjugate priors.IEEE Trans Signal Process 2013;61(13):3460–75.

8.Reuter S,Vo BT,Vo BN,Dietmayer K.The labeled multi-Bernoulli filter.IEEE Trans Signal Process 2014;62(12):3246–60.

9.Li XR,Bar-Shalom Y.A recursive multiple model approach to noise identification.IEEE Trans Aerosp Electron Syst 1994;30(3):671–84.

10.Storvik G.Particle filters in state space models with the presence of unknown static parameters.IEEE Trans Signal Process 2002;50(2):281–9.

11.Smidl V,Quinn A.Variational Bayesian filtering.IEEE Trans Signal Process 2008;56(10):5020–30.

12.Sarkka S,Nummenmaa A.Recursive noise adaptive Kalman filtering by variational Bayesian approximations.IEEE Trans Autom Control 2009;54(3):596–600.

13.Yang JL,Ge HW.Adaptive probability hypothesis density filter based on variational Bayesian approximation for multi-target tracking.IET Radar Sonar Navig 2013;7(9):959–67.

14.Zhang GH,Lian F,Han CZ,Han SY.An improved PHD filter Based on variational Bayesian method for multi-target tracking.IEEE international conference on information fusion.2014 July 7-10,Salamanca,Spain.Piscataway (NJ):IEEE Press;2014.p.1–6.

15.Wu XH,Huang GM,Gao J.Particle filters for probability hypothesis density filter with the presence of unknown measurement noise covariance.Chin J Aeronaut 2013;26(6):1517–23.

16.Wu XH,Huang GM,Gao J.Adaptive noise variance identification for PHD-based tracking algorithms using variational Bayesian approximations.IET Radar Sonar Navig2013;7(8):895–903.

17.Yang JL,Ge HW.An improved multi-target tracking algorithm based on CBMeMBer filter and variational Bayesian approximation.Signal Process 2013;93(9):2510–5.

18.Li CY,Wang R,Ji HB.Multiple extended-target tracking based on variational Bayesian cardinality-balanced multi-target multi-Bernoulli.Control Theory Appl 2015;32(2):187–95(Chinese).

19.Han K,Qin Z,Gao X.Dynamic particle allocation for CBMeMBer filter.IEEE international conference on information,communication and signal processing.2015 Dec 2–4,Singapore,Singapore.Piscataway (NJ):IEEE Press;2015.p.1–5.

20.Schuhmacher D,Vo BT,Vo BN.A consistent metric for performance evaluation of multi-object filters.IEEE Trans Signal Process 2008;56(8):3447–57.

Qiu Haoreceived the M.S.degree from Naval University of Engineering in 2012,where he is currently pursuing the Ph.D.degree.His main research interests are multi-target tracking and digital signal processing.

Huang Gaomingreceived the B.S.and M.S.degrees from Naval Electronic College of Engineering,Nanjing,China,in 1995 and 1998,respectively,and the Ph.D.degree in signal processing from Southeast University,Nanjing,China,in 2006.He is currently a professor at the College of Electronic Engineering,Naval University of Engineering,Wuhan,China.His main research interests are electronic warfare,blind signal processing and passive detection.

Gao Junis currently a professor at the Department of Communication Engineering,Naval University of Engineering,Wuhan,China.His research interests are signal processing and digital communications.

24 December 2015;revised 24 February 2016;accepted 9 April 2016

Available online 26 August 2016

Labeled random finite set;

Multi-Bernoulli filter;

Multi-target tracking;

Parameter estimation;

Variational Bayesian approximation

©2016 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

*Corresponding author.Tel.:+86 27 65461248.

E-mail address:qhcs01@163.com(Q.Hao).

Peer review under responsibility of Editorial Committee of CJA.