Plastic deformation analysis and forming quality prediction of tube NC bending
2016-11-24LuShiqingFngJunWngKelu
Lu Shiqing,Fng Jun,Wng Kelu
aNational Defense Key Disciplines Laboratory of Light Alloy Processing Science and Technology,School of Aeronautical Manufacturing Engineering,Nanchang Hangkong University,Nanchang 330063,China
bJiangxi Key Laboratory of Surface Engineering,Jiangxi Science and Technology Normal University,Nanchang 330013,China
Plastic deformation analysis and forming quality prediction of tube NC bending
Lu Shiqianga,*,Fang Juna,b,Wang Kelua
aNational Defense Key Disciplines Laboratory of Light Alloy Processing Science and Technology,School of Aeronautical Manufacturing Engineering,Nanchang Hangkong University,Nanchang 330063,China
bJiangxi Key Laboratory of Surface Engineering,Jiangxi Science and Technology Normal University,Nanchang 330013,China
Plane strain assumption and exponent hardening law are used to investigate the plastic deformation in tube bending.Some theoretical formulae including stress,curvature radius of neutral layer,angle of neutral layer deviation,bending moment,wall thickness variation and crosssection distortion,are developed to explain the phenomena in tube bending and their magnitudes are also determined.During unloading process,the springback angle is deduced using the virtual work principle,and springback radius is also given according to the length of the neutral layer which remains unchanged before and after springback.The theoretical formulae are validated by the experimental results or the validated simulation results in literature,which can be used to quickly predict the forming quality of tube numerical control(NC)bending.
1.Introduction
As the ability in satisfying the demands of high strength/weight ratio and impact energy absorption,bent tube parts have attracted more and more applications in various high technology industries,such as aviation,aerospace,automobile and shipbuilding.1,2Compared with other various bending methods such as press bending,stretch bending,pushing bendingand rolling bending,the numerical control bending(NC)is the most universal method to produce the bent tubes.However,the effects of coupling multi-factors and lack of proved theoretical instruction in tube NC bending result in the complexity in forming mechanism,and multi-defects such as wrinkling,over thinning,cross-section distortion and springback.Thus,great efforts have been conducted on the forming quality prediction of tube bending by experimental,theoretical and numerical approaches.
Wu et al.3experimentally investigated the effects of the temperature,bending velocity and grain size on the wall thickness change,cross-section distortion and springback of AM30 magnesium alloy tube in rotary draw bending.Liu et al.4,5experimentally obtained the effect of dies and process parameters on wall thickness distribution and cross-section distortion of thin-walled rectangular 3A21 aluminum alloy tube in NC bending.Tang6employed the plastic-deformation theory to deduce several bending related formulae such as stress distributions of bent tube,wall thickness variation,bending moment and flattening.Al-Qureshi and Russo7derived the approximate equations of tube bending to predict springback and residual stress quantitatively with assumptions of ideal elastic-plastic material,plane strain condition,absence of defects and''Bauschinger effectquot;.E et al.8derived an analytical formulae for the prediction of the stress distributions,neutral layer shift,wall thickness change and cross-section distortion based on in-plane strain assumption in tube bending with exponential hardening law.Li et al.9established the analytical prediction model for springback,which was considered tube specifications and material properties,using the plasticdeformation theory.The approximate equations were derived to predict bending moment and springback of bent tube considering the work hardening in the plastic-deformation region by Jeong et al.10The cross-section distortion formula was deduced based on virtual force principle by Liu et al.11It is noted that,though many factors cannot be considered such as contact conditions and unequal stress/strain distributions,the analytical models are still very useful to estimate and predict forming quality for tube bending.
Considering the complexity of tube bending forming,finite element(FE)numerical simulation method has been widely used to explore the bending deformation under various forming conditions.Fang et al.12,13established a three-dimensional FE model for high-strength 21-6-9 stainless steel tube in NC bending and revealed the effects of mandrel on wall thinning and cross-section distortion.By FE analysis,Li et al.14addressed the side push and booster push on wall thinning,crosssection distortion,and wrinkling occurring in NC bending of thin-walled aluminum alloy tubes.Murata et al.15numerically studied the effects of strain hardening exponent on wall thickness variation,cross-section distortion and springback during tube NC bending.Yang et al.16,17investigated the effects of friction on wall thinning,cross-section distortion and wrinkling of Al-alloy and stainless steel tubes in NC bending by using the FE method.In Ref.18,the coupling effects of the material parameters and the bending angle on springback for TA18 tube NC bending were researched by using FE simulation software ABAQUS.The springback mechanism for a large-diameter thin-walled CT20 titanium alloy tube in NC bending was revealed using numerical simulation method by Zhan et al.19
Although a large number of researches have been carried out to accelerate the development of tube bending technology,the theory of tube bending mechanism needs to be further studied because of the limitations of forming theories and the deficiency of stress test technologies.Thus,in this paper,some approximate formulae are derived to quantitatively predict wall thickness variation,cross-section distortion and springback based on plane strain assumption and virtual work principle in tube NC bending.The results are validated by the experimental results or validated simulation results in literature.
2.Plastic deformation analysis of tube NC bending
According to the plastic deformation theory and the geometrical feature of tube NC bending,the analytical models of tube bending are proposed in terms of stress distribution,neutral layer position,bending moment,wall thickness variation,cross-section distortion,and springback angle/radius.The assumptions are as follows:
(1)The uniform stress/strain distributions and the proportional loading are assumed.
(2)The cross-section of tube remains in a plane during bending,and the shear deformation of cross-section is negligible.
(3)The cross-section deformation of tube is not considered,namely the circumferential strain is regarded as zero.
(4)The stress-strain relation follows the exponent law as¯σ=K¯εn,where K is strength coefficient and n is hardening exponent.
(5)The material of tube is incompressible during bending process.
2.1.Stress analysis
According to the plane strain assumption and volume constant condition of plastic deformation,a strain field in tube bending can be determined by
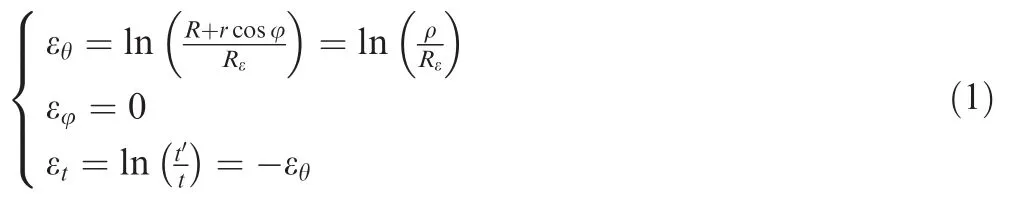
where εθ,εφ,and εtare tangential strain,hoop(circumferential)strain,and normal(thickness)strain,respectively;R is the centerline bending radius,Rεcurvature radius of neutral layer,ρ curvature radius of arbitrary fiber layer in tube wall,r the distance from any point in the cross-section to bending center,and φ the span angle;t and t′are wall thickness of tube before and after bending,respectively(see Fig.1).α is the angle of neutral layer deviation.
The stress-strain relation satisfies the total strain theory if the tube bending deformation satisfies the proportional loading condition(assumption(1))and it can be obtained as20

where σθ,σφand σtare tangential stress,hoop stress,and normal stress,respectively;¯σ and¯ε denote equivalent stress and equivalent strain,respectively.
By substituting Eq.(1)into Eq.(2),the normal stress σtcan be deduced as

Under the plane strain condition,equivalent stress¯σ and equivalent strain ¯ε can be obtained as20
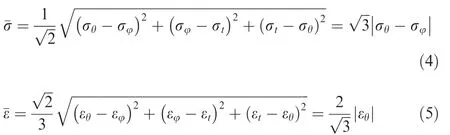
By substituting Eqs.(1),(4)and(5)into the exponent strain hardening law¯σ=K¯εn,therelationship between tangential stress and hoop stress can be deduced as
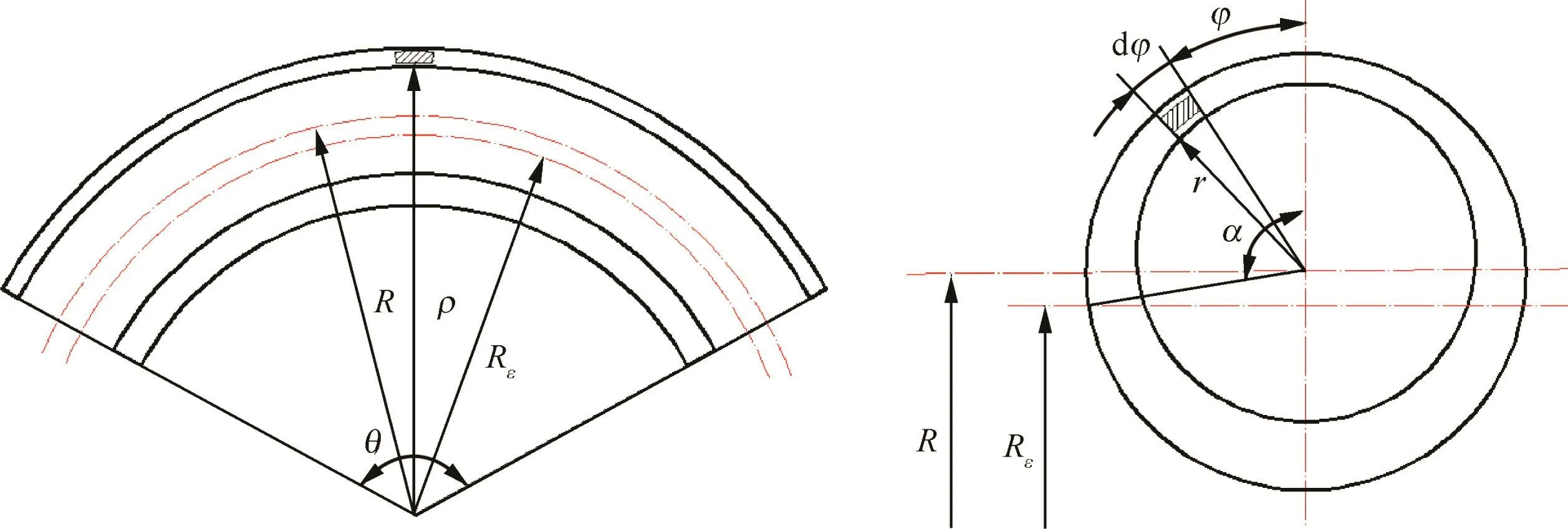
Fig.1 Schematic diagram of bent tube.

When ρ gt;Rε,the plus sign''+quot;is taken,otherwise the minus sign''-quot;is taken.
Stress equilibrium differential equation in hoop direction can be expressed as(the detailed derivation process is shown in Appendix A)

Integrating Eq.(7),the hoop stress σφcan be obtained as
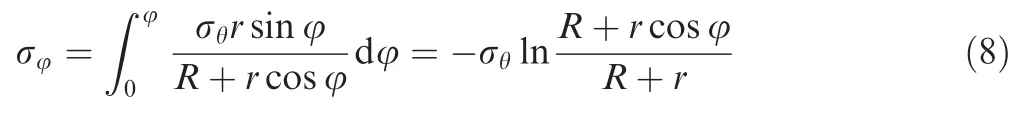
By using r=D/2 and m=R/D,where D is initial outer diameter of tube,the hoop stress σφcan befurther written as
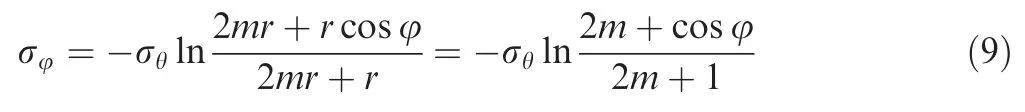
The range of m in this paper should be great than or equal to 2 to make the error smaller(the detailed discussion process is shown in Appendix B).When the m≥2,the logarithmic part of Eq.(9)can be simplified as
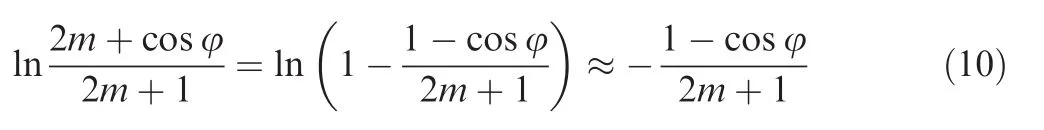
Therefore,the relationship between tangential stress and hoop stress can be expressed as

Substituting Eq.(11)into Eq.(6),the tangential stress σθcan be deduced as

where σθoand σθidenote tangential stress on the outer side and inner side of the tube wall,respectively.
Incorporating Eqs.(11)–(13),the hoop stress σφis presented as
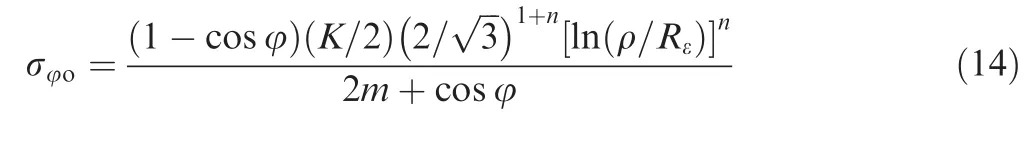
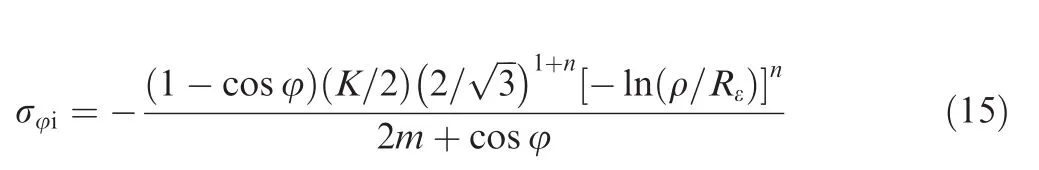
where σφoand σφidenote hoop stress on the outer side and inner side of the tube wall,respectively.
Substituting Eqs.(12)–(15)into Eq.(3),the normal stress σtis calculated as
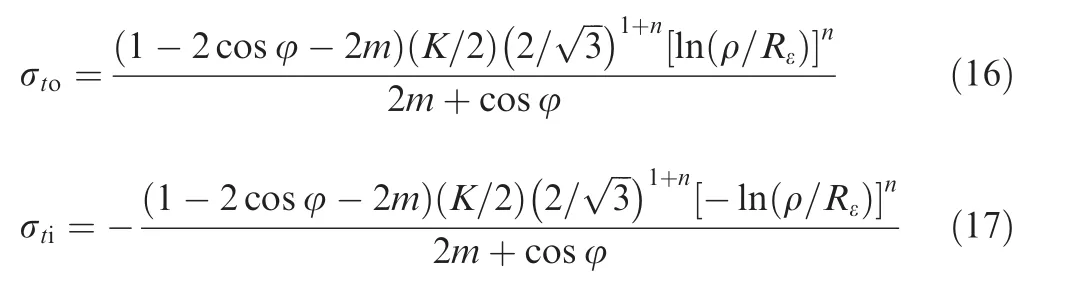
where σtoand σtidenote normal stress on the outer side and inner side of the tube wall,respectively.
2.2.Neutral layer deviation
The curvature radius of neutral layer for any cross-section can be expressed as21

where A denotes the area of cross-section, and A= πD2/4-π(D-2t)2/4 is taken for the tube.
From the Eq.(18),the curvature radius of neutral layer Rεcan be obtained as

Since D≫t,Eq.(19)can be simplified as

The amount of neutral layer deviation Encan be obtained as En=R-Rε,while Enin literature6is calculated as

The relationship among Rε,R and the angle of neutral layer deviation α(shown in Fig.1)can be expressed as

Substituting Eq.(20)into Eq.(22),the angle of neutral layer deviation α can be calculated as
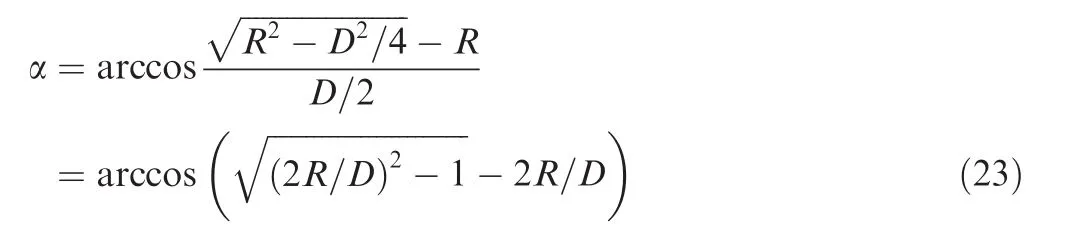
2.3.Bending moment calculation
The distance between tensile/compressive fiber of tube and neutral layer is y.y is positive value for tensile fiber,while y is negative value for compressive fiber.In the neutral layer position,y is zero as shown in Fig.2.
When 0≤ φ ≤ 2π,the y can be obtained as

And the value range of y can be determined by
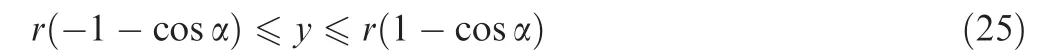
Then,the bending moment M can be expressed as
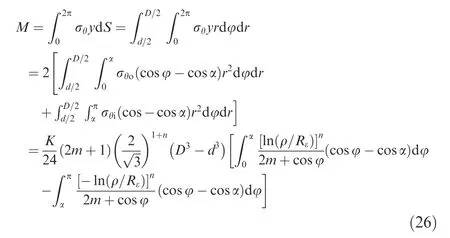
where d is the inner diameter of tube.
3.Forming quality prediction of tube NC bending
3.1.Wall thickness variation
Based on the plane strain assumption and considering neutral layer deviation,the wall thinning ratio Δtoand wall thickening ratio Δtican be derived as(the detailed derivation process is shown in Appendix C)
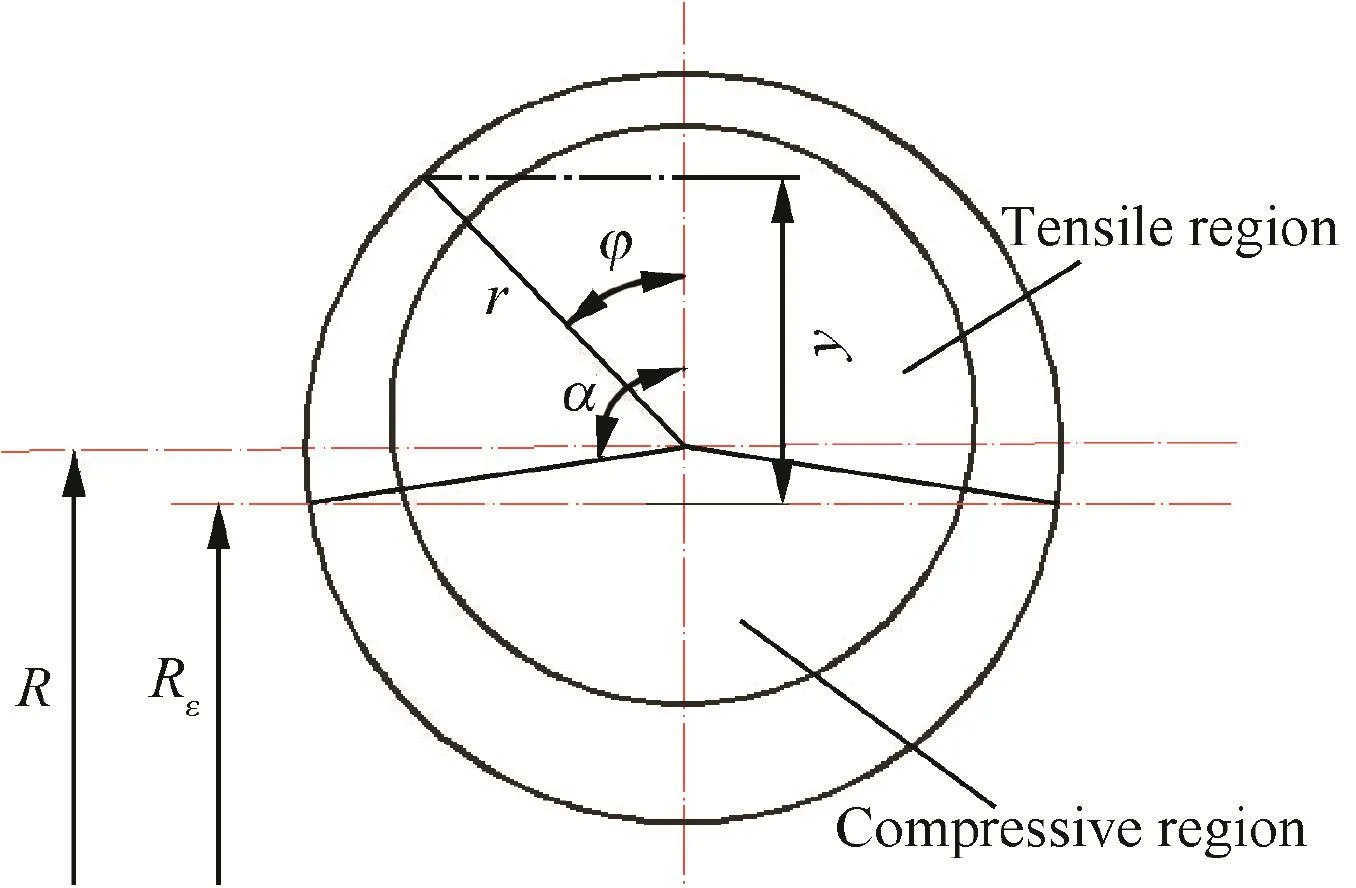
Fig.2 Distance between tangential fiber and neutral layer.
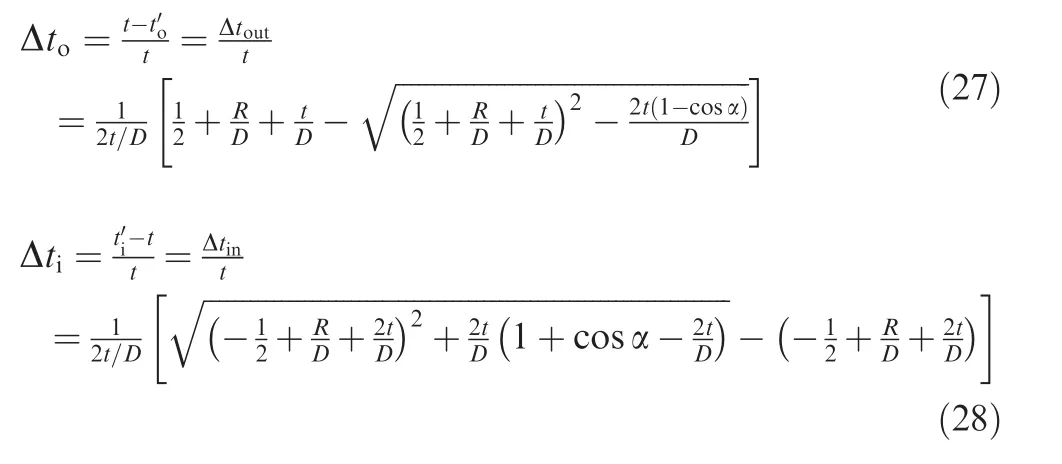
As can be seen from Eqs.(27)and(28),the wall thickness variation is related to the relative bending radius R/D,the relative wall thickness of tube t/D and the angle of neutral layer deviation α.
3.2.Cross-section distortion
During tube NC bending process,tangential tensile stress subjected to the outer material of bent tube will lead to wall thickness thinning,while tangential compressive stress subjected to the inner material of bent tube will lead to wall thickness thickening.Meanwhile both the resultant force of tangential stress of inner part and that of outer part point to the center of cross-section of tube,which leads to the cross-section distortion as shown in Fig.3,where F denotes the tangential tensile force and M the bending moment.
Based on the plane strain assumption,the hoop deformation of the bent tube is neglected.The tube is constrained in transverse direction(major axis)by bending die groove and under free deformation conditions in vertical direction(minor axis)in bending process.Thus,the changing ratio of minor axis is often adopted to describe the severity of cross-section distortion in engineering application.
It is assumed that the wall thickness changes uniformly along the axial direction of the tube and hoop deformation is not considered.The changing ratio of outer diameter of minor axis ΔD can be expressed as
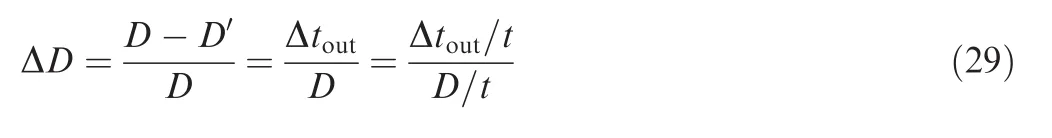
where D′denotes the minimum outer diameter of minor axis for the distorted cross-section.
Substituting Eq.(27)into Eq.(29),ΔD can be further obtained as
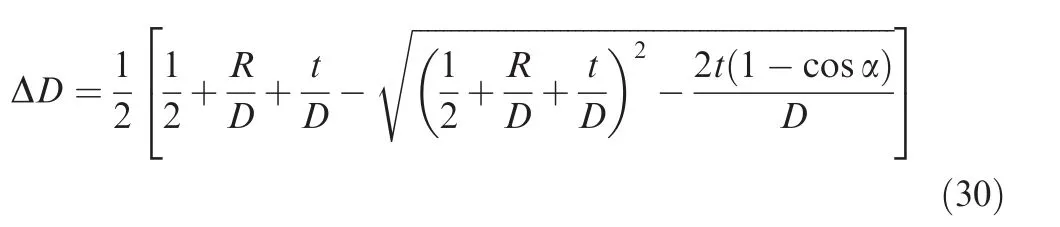
Similarly
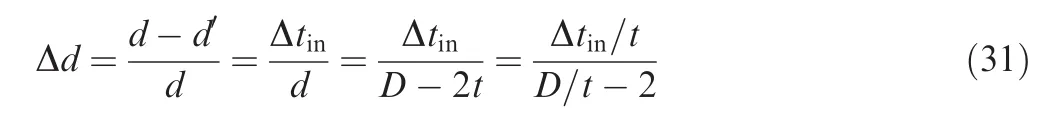
where Δd denotes the changing ratio of inner diameter of minor axis and d′the minimum inner diameter of minor axis for the distorted cross-section.
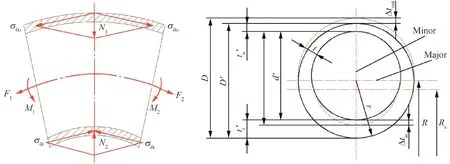
Fig.3 Cross-section distortion in bending process under plane strain condition.
Substituting Eq.(28)into Eq.(31),Δd can be further expressed as
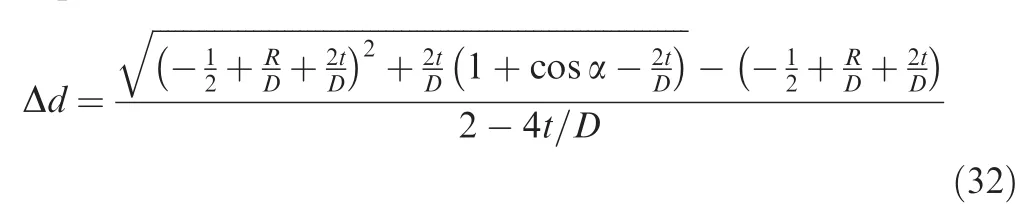
As can be seen from Eqs.(30)and(32)that the crosssection distortion is also related to the relative bending radius R/D,the relative wall thickness of tube t/D and the angle of neutral layer deviation α.
3.3.Springback
Bent tube can be considered as statically determinate structure before unloading.One end of the bent tube is regarded as fixed,and the other is free when unloading occurs momentarily.The reverse loading bending moment Muis equal to the loading bending moment M,but the direction is opposite.Springback is a question of small disturbance of elastic deformation,which can be calculated by the virtual work principle.
The reverse bending moment Muis loaded on free end of bent tube,and the virtual unit bending moment MTand MSare loaded on sectional T and S,respectively.Sectional T and S are assumed as the cross-section of the starting bending point and ending bending point of tube,respectively;θ is a bending angle,as shown in Fig.4.The relative rotation angle of sectional T and S can be regarded as springback angle of the bent tube.
The actual state equation of bent tube springback can be expressed as


Fig.4 Virtual state for bent tube springback.
The virtual state equation of bent tube springback based on virtual force principle can be expressed as

According to the virtual force principle,the springback angle Δθ can be calculated as

where E denotes elasticity modulus;I is the moment of inertia of cross-section after bending,and the value is 0.7 times of that before bending.22
The moment of inertia of cross-section after bending can be calculated as

Substituting Eqs.(20),(26)and(37)into Eq.(36),Δθ can be further obtained as
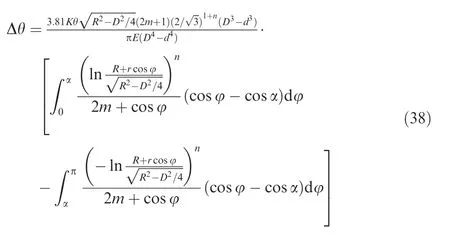
The length of the neutral layer remains unchanged before and after springback,thus the curvature radius of neutral layer after springback can be calculated as

where Rfdenotes the curvature radius of neutral layer after springback;θ′is the actual forming angle.
Then,the radius growth ΔR after springback can be obtained as

4.Evaluation of theoretical results
Based on the neutral axis deviation theoretical analysis,a calculation example was carried out.The parameters of the example are as follows:
The outside diameter of tube D is 10 mm,the wall thickness of the tube t is 1 mm and relative bending radius R/D is 2.5.
The neutral axis deviation Enin the paper is
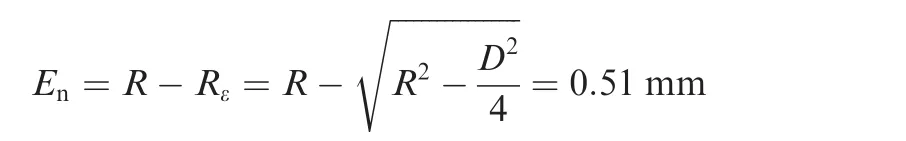
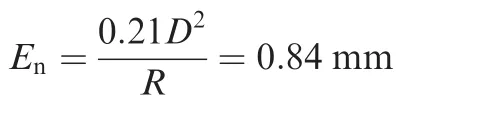
For thin-walled tube bending with small diameter under non-mandrel condition and the relative bending radius R/Dgt;2,the neutral axis deviation Enis less than 0.8 mm.23Therefore,the neutral axis deviation formula in the paper is better than that in Ref.6.
Fig.5 shows the comparison of wall thickening ratio between calculation and experimental results.The 1Cr18Ni9Ti stainless steel tube NC bending with the specification of 28 mmX1 mm(DXt)was carried out by the NC tube bender VB300HP in literature.24It can be seen from Fig.5 that the change trend of theoretical calculation results of wall thickening ratio is consistent with that of experimental results.Namely the wall thickening ratio decreases with the increase of relative bending radius.Compared with the experimental results,the average relative error and maximum relative error of the theoretical results of Ref.8 are 31.21%and 35.30%,respectively;the average relative error and maximum relative error of the theoretical results of Ref.6 are 29.87%and 35.96%,respectively;while the average relative error and maximum relative error of the theoretical results of the paper are 14.97%and 17.88%,respectively.As a whole,the analytical calculation results of the paper are closer to the experimental results when compared to the results of literature,6,8which can fully satisfy the project requirements for the fast predication of the forming quality defects of tube bending.This is because the neutral layer shift is considered in the paper,while that is neglected in the literature.6,8

Fig.5 Calculation and experimental results for wall thickening ratio.
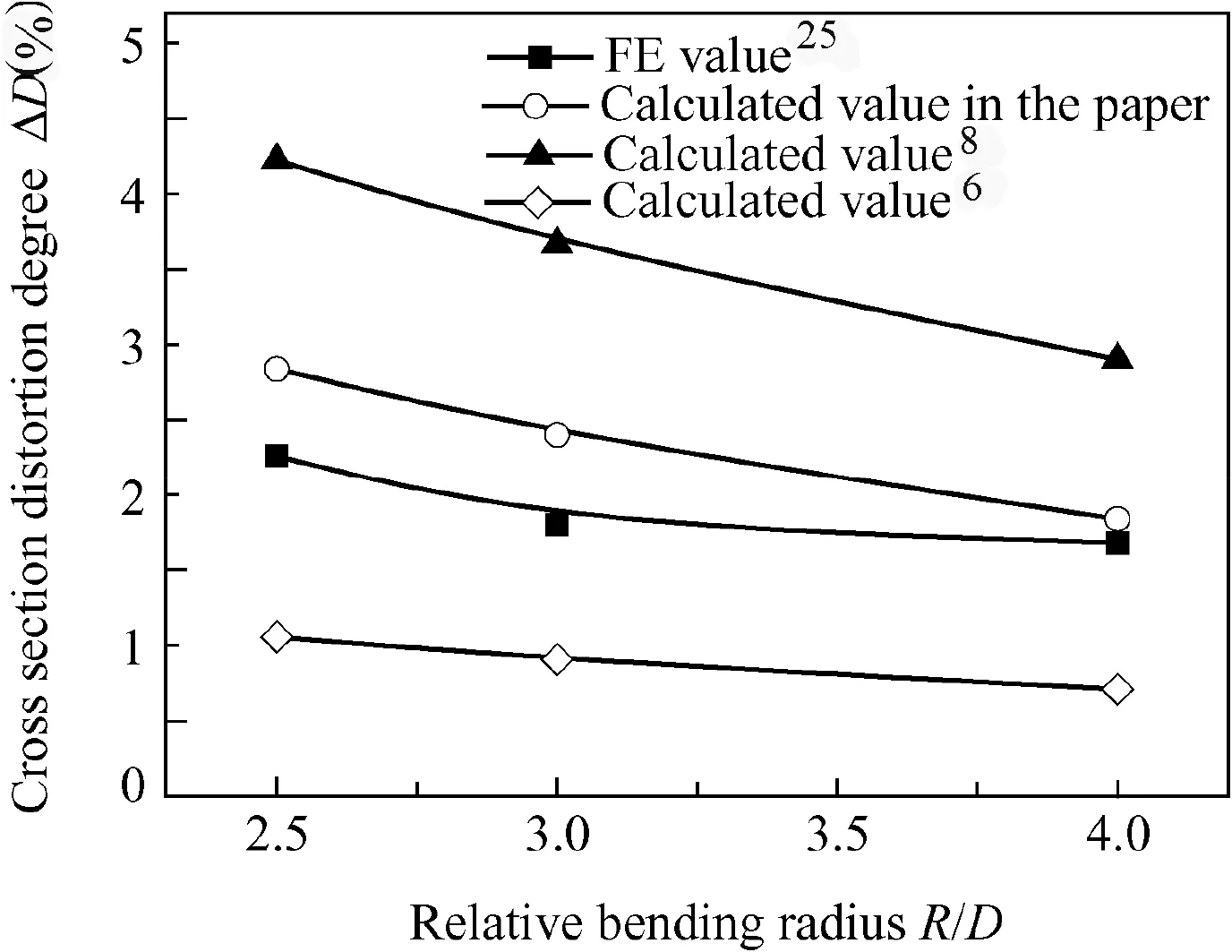
Fig.6 Calculation and validated simulation results for crosssection distortion degree.
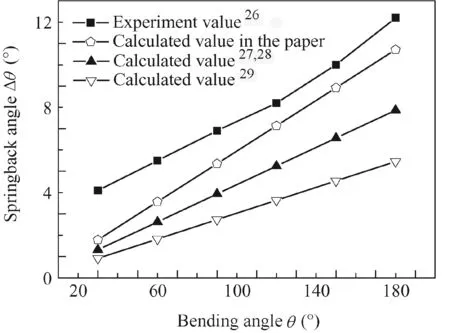
Fig.7 Calculation and experimental results for springback angle.
Fig.6 shows a comparison between calculation results and simulation results validated by experiment in literature25for cross-section distortion degree.It can be seen from Fig.6 that the change trend of analytical calculation results of crosssection distortion degree is consistent with that of simulation results.Viz.the cross-section distortion degree decreases with the increase of relative bending radius.Compared with the simulation results,the average relative error and maximum relative error of the analytical results of Ref.8 are 87.87%and 103.71%,respectively;the average relative error and maximum relative error of the analytical results of Ref.6 are 53.54%and 57.83%,respectively;while the average relative error and maximum relative error of the analytical results of the paper are 22.78%and 33.39%,respectively.By the large,the analytical calculation results of the paper compared with that of literature6,8is closer to the validated simulation results.This is also because the neutral layer shift is considered in the paper,while that is not considered in the literature.6,8
Fig.7 shows a comparison of springback angle between calculation and experimental results of 21-6-9 high strength stainless steel tube NC bending with the specification of 6.35 mmX0.41 mmX20 mm(DXtXR)in literature.26It is discovered that the change trend of the analytical calculation results of springback angle is consistent with that of the experimental results.Viz.with the increase of bending angle,the springback angle increases.Compared with the experimental results,the average relative error of analytical results of the literature27,28is 44.90%,the maximum relative error of 68.02%is located at the bending angle of 30°;the average relative error of analytical results of the literature29is 61.77%,the maximum relative error of 77.82%is also located at the bending angle of 30°;while the average relative error of the analytical results of the paper is 25.00%and the maximum relative error of 56.48%is also located at the bending angle of 30°.Furthermore,when the bending angle is larger than 90°,the relative error is less than 15.00%.On the whole,the analytical calculation results of the paper compared with that of literature27–29is closer to the experimental results.This is because that the 3D stress/strain,moment of inertia of cross-section variation and neutral layer deviation are considered in the paper,while the 3D stress/strain is neglected,and the material is simplified into the ideal elastic–plastic material in literature;27,28the moment of inertia of cross-section variation and neutral layer deviation are not considered in literature.29
The error is larger at smaller bending angle in the paper.This is because that the smaller plastic deformation zone,material inhomogeneity,workpiece shape,and dimension inconformity lead to the larger impact on the small bending angle.28The effect of the axis force on springback is neglected,and the frictional condition and multi-die dynamic constraint are not considered in tube bending process,which will introduce errors for the analytical results.
Through the above analysis,it is known that the precision of the analytical model in this paper is higher than that of the literature.Thus,the model can be used to quickly predict the forming quality of tube NC bending.
5.Conclusions
(1)Based on the plane strain assumption and exponent hardening law,the approximate formulae of stress,curvature radius of neutral layer,angle of neutral layer deviation and bending moment of tube NC bending are derived.
(2)Wall thinning ratio,wall thickening ratio,changing ratio of outer diameter of minor axis and changing ratio of inner diameter of minor axis of tube NC bending are deduced under the plane strain assumption and considering neutral layer deviation.
(3)The springback angle of bent tube is derived according to the virtual work principle,and the springback radius is derived on condition that the length of the neutral layer remains unchanged before and after springback.
(4)The analytical models are validated by the experimental results or the simulation results validated in literature,which can be used to quickly predict the forming quality of tube NC bending.
Acknowledgements
The authors would like to thank the National Natural Science Foundation of China(No.51164030)and National Defense Key Disciplines Laboratory of Light Alloy Processing Science and Technology,Nanchang Hangkong University(No.gf201501001)for the support on this research.
Appendix A
The differential element body stress analysis of bent tube is shown in Fig.A1.The centripetal composite force of tangential stress N is
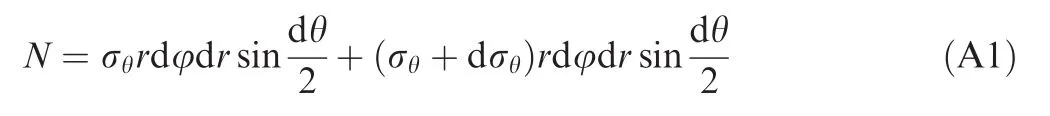
For the small angles here take

Substituting Eq.(A2)into Eq.(A1)and neglecting the product of infinitesimal,the Eq.(A1)can be simplified as

Stress equilibrium differential equation in hoop direction can be expressed as

Substituting Eq.(A3)into Eq.(A4),Eq.(A4)can be simplified as

Therefore,the differential relationship between hoop stress and tangential stress can be obtained as

Appendix B
As

The Taylor development is expressed as follows:
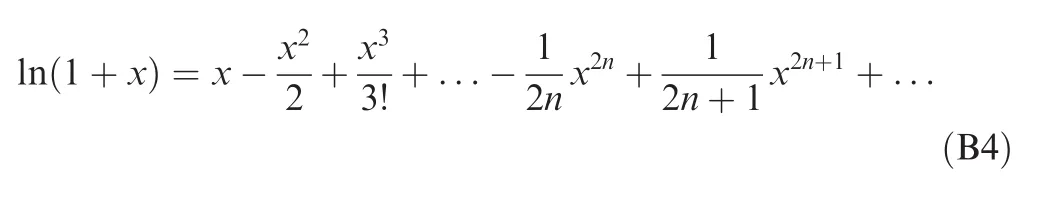
To make ln(1+x)≈x hold,one condition must be satisfied,that is

For example
10%error may request:

In Eq.(10)

20%error may request:


Fig.A1 Differential element body stress analysis of bent tube.

30%error may request:
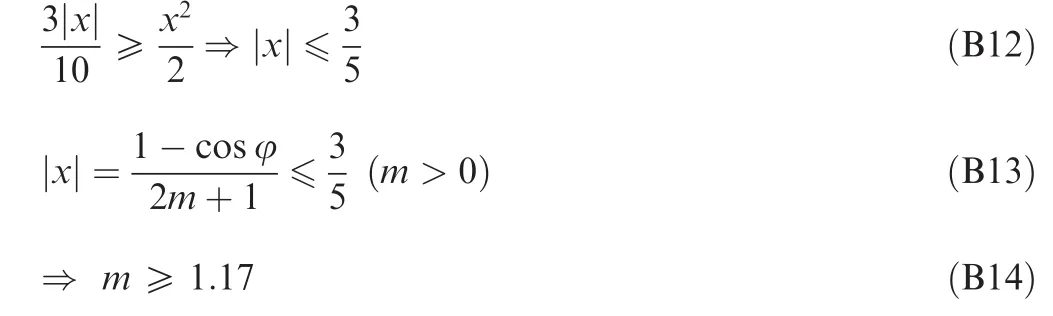
Appendix C
According to εθ=-εt, εφ=0 and considering neutral layer deviation,the equation can be obtained as
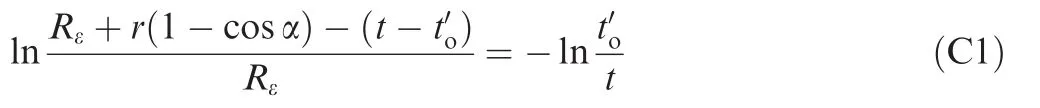
Taking the logarithm for Eq.(C1)and substitutinginto Eq.(C1),Eq.(C1)can be simplified as
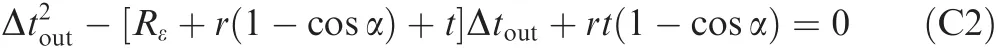
Substituting r=D/2 into Eq.(C2),Δtoutcan be obtained as
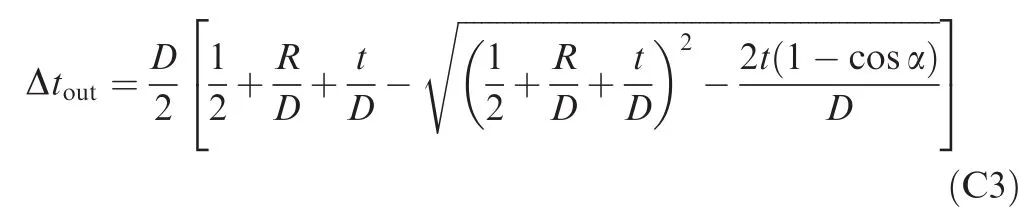
Therefore,the wall thinning ratio Δtocan be derived as
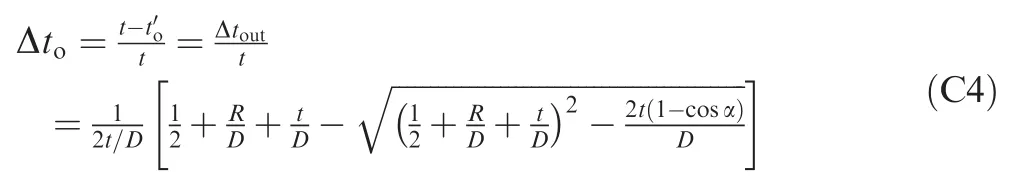
Similarly,the wall thickening ratio Δtican be determined by the following equation
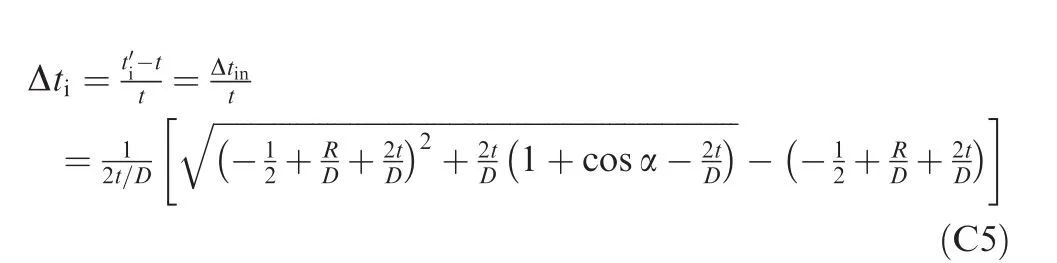
1.Ahmetoglu M,Altan T.Tube hydroforming:state-of-the -art and future trends.J Mater Process Technol 2000;98(1):25–33.
2.Yang H,Li H,Zhang ZY,Zhan M,Liu J,Li GJ.Advances and trends on tube bending forming technologies.Chin J Aeronaut 2012;25(1):1–12.
3.Wu WY,Zhang P,Zeng XQ,Li J,Yao SS,Luo AA.Bendability of the wrought magnesium alloy AM30 tubes using a rotary draw bender.Mater Sci Eng,A 2008;486(1–2):596–601.
4.Liu KX,Liu YL,Yang H,Zhao GY.Experimental study on cross-section distortion of thin-walled rectangular 3A21 aluminium alloy tube by rotary draw bending.Int J Mater Prod Technol 2011;42(1–2):110–20.
5.Liu KX,Liu YL,Yang H.Experimental study on the effect of dies on wall thickness distribution in NC bending of thin-walled rectangular 3A21 aluminum alloy tube.Int J Adv Manuf Technol 2013;68(5–8):1867–74.
6.Tang NC.Plastic-deformation analysis in tube bending.Int J Pres Vessels Pip 2000;77(12):751–9.
7.Al-Qureshi HA,Russo A.Spring-back and residual stresses in bending of thin-walled aluminium tubes.Mater Des 2002;23(2):217–22.
8.E DX,Chen JS,Ding J,Bai X.In-plane strain solution of stress and defects of tube bending with exponential hardening law.Mech Based Des Struct Mach:Int J 2012;40(3):257–76.
9.Li H,Yang H,Song FF,Zhan M,Li GJ.Springback characterization and behaviors of high-strength Ti-3Al-2.5V tube in cold rotary draw bending.J Mater Process Technol2012;212(9):1973–87.
10.Jeong HS,Ha MY,Cho JR.Theoretical and FE analysis for inconel 625 fine tube bending to predict springback.Int J Precis Eng Manuf 2012;13(12):2143–8.
11.Liu JY,Tang CT,Ning RX.Deformation calculation of cross section based on virtual force in thin-walled tube bending process.Chin J Mech Eng 2009;22(5):696–701.
12.Fang J,Lu SQ,Wang KL,Yao ZJ.Three-dimensional finite element model of high strength 21-6-9 stainless steel tube in rotary draw bending and its application.Indian J Eng Mater Sci 2015;22(2):142–51.
13.Fang J,Lu SQ,Wang KL,Xu JM,Xu XM,Yao ZJ.Effect of mandrel on cross section quality in numerical control bending process of stainless steel 2169 small diameter tube.Adv Mater Sci Eng 2013;2013:1–9.
14.Li H,Yang H,Zhan M,Kou YL.Deformation behaviors of thinwalled tube in rotary draw bending under push assistant loading conditions.J Mater Process Technol 2010;210(1):143–58.
15.Murata M,Kuboki T,Takahashi K,Goodarzi M,Jin Y.Effect of hardening exponent on tube bending.J Mater Process Technol 2008;201(1):189–92.
16.Yang H,Gu RJ,Zhan M,Li H.Effect of frictions on cross section quality of thin-walled tube NC bending.Trans Nonferrous Met Soc China 2006;16(4):878–86.
17.Yang H,Li H,Zhan M.Friction role in bending behaviors of thinwalled tube in rotary-draw-bending under small bending radii.J Mater Process Technol 2010;210(15):2273–84.
18.Jiang ZQ,Yang H,Zhan M,Xu XD,Li GJ.Coupling effects of material properties and the bending angle on the springabck angle of a titanium alloy tube during numerically controlled bending.Mater Des 2010;31(4):2001–10.
19.Zhan M,Zhai HD,Yang H.Springback mechanism and compensation of cryogenic Ti alloy tube after numerically controlled bending.Trans Nonferrous Met Soc China 2012;22(Suppl.2):s287–93.
20.Yu HQ,Chen JD.Principle of met al plastic forming.Beijing:China Machine Press;2004.p.107–10[Chinese].
21.Liu HW.Mechanics of materials.5th ed.Beijing:Higher Education Press;2011.p.152–9[Chinese].
22.Wang WC,Stelson KA.Computer aided manufacturing for threedimensional tube bending with on-line springback compensation.Trans NAMRI/SME 1991;70–6.
23.E DX,Guo XD,Ning RX.Analysis of strain neutral layer displacement in tube-bending process.J Mech Eng 2009;45(3):307–10[Chinese].
24.Cheng PZ.Research on quality forecast and parameters optimization technology of NC tube bending[dissertation].Beijing:Beijing Institute of Technology;2010[Chinese].
25.Fang J,Lu SQ,Wang KL,Xu XM,Xu JM,Yao ZJ.FE analysis of section distortion in numerical control bending of the 0Cr21Ni6Mn9N stainless steel tube.J Plast Eng 2013;20(5):71–6[Chinese].
26.Fang J,Lu SQ,Wang KL,Yao ZJ.Springback law of high strength 21-6-9 stainless steel tube in NC bending under different process parameters.Proc IMechE Part B-J Eng Manuf 2015;26(3):379–84.
27.E DX,He HH,Liu XY,Ning RX.Spring-back deformation in tube bending.Int J Min Met Mater 2009;16(2):177–83.
28.Liu JW,Ni XD,Gao WG.Modeling and analyzing the bending re-spring angle of pipe Q235-A.Modern Manuf Eng 2003(5);51–2[Chinese].
29.Zhang LL.Calculation of springback in pipe bending.Forg Stamp Technol 2002(3);37–9[Chinese].
Lu Shiqiangis a professor and Ph.D.supervisor at School of Aeronautical Manufacturing Engineering,Nanchang Hangkong University.He received the Ph.D.degree from Northwestern Polytechnical University.His main research interests are plastic deformation theory and technology of difficult to deform materials,finite element simulation of plastic forming process.
Fang Junreceived Ph.D.degreefrom Nanjing University of Aeronautics and Astronautics in 2015.He is now a teacher in Jiangxi Scienceamp;Technology Normal University.His main research interests are advanced plastic forming and multi-scale modelingamp;simulation.
Wang Keluis a professor and Ph.D.supervisor with Ph.D.degree.His main research interest lies in precision plastic forming theory and technology.
2 November 2015;revised 12 January 2016;accepted 20 February 2016
Available online 26 August 2016
Forming quality;
Plane strain;
Tube NC bending;
Theoretical analysis;
Virtual work principle
©2016 Production and hosting by Elsevier Ltd.on behalf of Chinese Society of Aeronautics and Astronautics.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
*Corresponding author.
E-mail address:niatlusq@126.com(S.Lu).
Peer review under responsibility of Editorial Committee of CJA.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Flapping wing micro-aerial-vehicle:Kinematics,membranes,and flapping mechanisms of ornithopter and insect flight
- A new non-linear vortex lattice method:Applications to wing aerodynamic optimizations
- Experimental study of flow field distribution over a generic cranked double delta wing
- Streamwise-body-force-model for rapid simulation combining internal and external flow fields
- An artificial neural network approach for aerodynamic performance retention in airframe noise reduction design of a 3D swept wing model
- effects of wing locations on wing rock induced by forebody vortices
