Active fault tolerant control for vertical tail damaged aircraft with dissimilar redundant actuation system
2016-11-24WngJunWngShopingWngXingjinShiCunMiletTomovic
Wng Jun,Wng Shoping,Wng Xingjin,*,Shi Cun,Milet M.Tomovic
aSchool of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China
bCollege of Engineering and Technology,Old Dominion University,Norfolk,VA 23529,USA
Active fault tolerant control for vertical tail damaged aircraft with dissimilar redundant actuation system
Wang Juna,Wang Shaopinga,Wang Xingjiana,*,Shi Cuna,Mileta M.Tomovicb
aSchool of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China
bCollege of Engineering and Technology,Old Dominion University,Norfolk,VA 23529,USA
This paper proposes an active fault-tolerant control strategy for an aircraft with dissimilar redundant actuation system (DRAS) that has suffered from vertical tail damage.A damage degree coefficient based on the effective vertical tail area is introduced to parameterize the damaged flight dynamic model.The nonlinear relationship between the damage degree coefficient and the corresponding stability derivatives is considered.Furthermore,the performance degradation of new input channel with electro-hydrostatic actuator (EHA) is also taken into account in the damaged flight dynamic model.Based on the accurate damaged flight dynamic model,a composite method of linear quadratic regulator (LQR) integrating model reference adaptive control (MRAC) is proposed to reconfigure the fault-tolerant control law.The numerical simulation results validate the effectiveness of the proposed fault-tolerant control strategy with accurate flight dynamic model.The results also indicate that aircraft with DRAS has better fault-tolerant control ability than the traditional ones when the vertical tail suffers from serious damage.
1.Introduction
Structural damage to an aircraft,like the damage/loss of a vertical tail,can lead to loss of controllability,which would createa challenging situation for the pilots.1–3An example of such a situation,is the disaster that involved the Boeing 747 freighter aircraft that crashed in Mount Osutaka in 1985,with no one survived(520 fatalities).In this particular case,the aircraft lost the vertical tail and the hydraulic pipelines were pulled apart.This damage caused significant loss of controllability and,next to that,structural changes,which led to the crash.Another such similar example was 2001-A300,vertical tail loss,265 fatalities.Such failures were likely to be survivable,if given correct control input and a wise trajectory.However,there were no effective measures for these aircraft with traditional centralized hydraulic actuation system(HAS)in such extreme situations,since the vertical tail loss would pull apart the hydraulic pipelines and lead the aircraft to lose pressures to actuate.Fortunately,the modern civil aircraft are developing toward the trend of being powered electrically more and more.Electrohydrostatic actuators (EHA) have been applied in aircraft together with traditional centralized HAS,which produces dissimilar redundant actuation system (DRAS).4,5Consequently,there has been a growing interest in new-type aircraft with this kind of new actuation system.The commercial aircraft,A380,A350 and A400M of Airbus Company have adopted DRAS of 2H/2E type.Researches about DRAS are being done as one effective measure to further enhance the flight safety.6These researches indicate that aircraft with DRAS have potential fault-tolerant capability to respond to some extreme situations.Therefore,it is desirable to develop fault-tolerant mechanisms for aircraft with DRAS that can assist the crew in some severe situations.
Outer mold line changes due to the damage can result in nonlinear and/or non-symmetric mass properties,aerodynamics,or control characteristics.7Though it is difficult to analytically estimate or predict such characteristics or their impact,it is still very necessary to study the relationship between the damage degree and the dynamic model to service the fault-tolerant control (FTC) strategy design.The general effects of vertical tail damage on directional characteristics are similar in nature to those seen in the pitch axis from stabilizer damage,namely,a reduction in static and dynamic stability.Much earlier work has been done to study the damaged aircraft modeling and the fault-tolerant strategy.8–10In these researches,the researchers studied the damaged aircraft model with vertical tail loss with not very serious damage using Boeing-747 100/200 data and regarded the input channel can continue to work.However,it is highly possible for the aircraft only with centralized HAS to lose the input channel when suffering from serious vertical tail loss.Besides,in these researches,the damage-induced aerodynamics characteristics change is expressed as a linear scale of the maximum damage degree,the accurate nonlinear relationship between the damage degree and its corresponding stability and control derivatives has not been studied.
For the research about vertical tail loss,10since the researchers studied the not very serious damage degree,three passive fault-tolerant control (PFTC) methods:quadratic stabilization,guaranteed cost control and quadratic cost control with robust pole placement were compared.The conclusion is that guaranteed cost control with robust pole placement can have a better control performance when the damage is less than 10%.However,when the damage degree exceeds a critical number,those PFTC methods would be no longer applicable.An active fault-tolerant control (AFTC)11–15method should be chosen to respond to extreme situations.Many researchers developed effective control methods to cope with FTC problems of complex system.In Li and Yang's latest research work,16an adaptive fuzzy decentralized control method was used to solve the FTC problem of large-scale nonlinear systems with actuator faults and unknown dead zone;in their another work,17a robust fuzzy adaptive control method was used to solve the FTC problem of large-scale nonlinear systems with mismatched uncertainties and actuator faults.Both researches indicate the effectiveness of adaptive technique as one important factor of the control method.To compensate for the serious failures of aircraft,Stengel and Huang studied reconfigurable control using proportional-integral implicit model following method very early.18Bodson and Groszkiewicz developed a multivariable adaptive algorithm for reconfigurable flight control system.19Bosˇkovic and Mehra developed an adaptive control method for a tailless advanced fighter aircraft under wing damage.20The later researches,e.g.in Lavretsky's research,an composite model reference adaptive control (MRAC) method was developed by integrating the classical model following method and adaptive control.21These researches indicate that MRAC can be an effective FTC method and it is necessary to highlight that in flight control system the determination of control law parameters should be more efficient.
This paper studies the civil aircraft with DRAS and focuses on the modeling of damaged aircraft in vertical tail loss situation and developing FTC strategy.A damage degree coefficient based on the effective vertical tail area is introduced,and the n the nonlinear relationship between the damage degree and its corresponding stability and control derivatives are studied.In this way,a flight dynamic model for a damaged aircraft is developed to account for various damage degrees that result in changes to aerodynamics.Furthermore,even the hydraulic systems lose pressure when the pipelines are pulled apart due to vertical tail loss,EHA can continue to actuate to stabilize the dynamic model.Therefore,the performance of EHA is also modeled in the dynamic model.Based on the accurate modeling,an AFTC strategy,using MRAC composed of linear quadratic regulator (LQR) technique,22,23is developed.In this way,the control law parameters can be determined by LQR method while the fault-tolerance can be guaranteed by MRAC method.Simulation results illustrate the necessity of accurate modeling and effectiveness of designed FTC strategy.
2.Modeling of damaged aircraft
It is a standard practice to linearize the model around a certain steady flight operating point.When the aircraft suffers from vertical tail damage,only some lateral-directional parameters change,therefore,only the lateral-directional model of the aircraft was considered in this paper.Using the early research work,10,24the aircraft model under normal conditions can be represented as follows:
where the state variable vector x=[β, p, r, φ]T,in which β is the sideslip angle,p the roll rate,r the yaw rate,and φ the roll angle;the system corresponding matrices are

Forthe system matrices,the nomenclature for all the parameters in matrices A and B is the same as in Li and Liu's research work.10Where,and Izare inertia moments about
(x,z)axes respectively;Izxis the inertia product due to(x,z)axes;Yβ,Ypand Yrare the side aerodynamic forces in three stability axes respectively;Lβ,Lpand Lrare the rolling moments in three stability axes respectively;Nβ,Npand Nrare the yawing moments in three stability axes respectively;YδaandYδrare side aerodynamic forces provided by ailerons and rudders respectively;Lδaand Lδrare the rolling moments provided by ailerons and rudders respectively;Nδaand Nδrare the yawing moments provided by ailerons and rudders respectively;m is the total mass of the airplane;u0is the reference flight speed;θ0is the reference angle of climb;g0is the acceleration due to gravity.
uH=[δa, δr]Tis the control input vector,and δathe control input provided by ailerons,δrthe control input provided by rudders.The output matrix C indicates that sideslip angle β and roll angle φ are the system output.
In this section,the aircraft dynamic model has been well developed.An accurate model can be obtained by considering the nonlinear damage of vertical tail and the performance degradation of EHA.
2.1.Modeling of nonlinear damage
2.1.1.Modeling of vertical tail damage
For aircraft suffering from vertical tail damage,as shown in Fig.1,the fracture shape caused by vertical tail loss is irregular and some relative assumptions are made for the proceeding of the research.
Assumption 1.The vertical tail shape is regular trapezium and the loss part of vertical tail is equivalent to regular trapezium.
Based on Assumption 1,a parameter μ is introduced to define the damage degree.
Definition 1.Vertical tail damage coefficient μ:the ratio of lost effective area in all effective areas of the vertical tail.
With the above definition,μ∈[0,1]can be used to represent different damage cases,especially,μ=0 represents that the flight model is in normal condition without damage.In order to obtain the nonlinear relationship between μ and all the corresponding stability derivative deviation,the fundamental equation of vertical tail derivative in Eq.(2)is used as

Fig.1 An aircraft with irregular partial vertical tail loss.

where Cyβis the damaged vertical tail derivative;β2=1-Ma2,F=1.07(1+d/b)2,with Ma the Mach number,b the height of vertical tail and d the fuselage diameter;Soutand Srefare exposed area and reference area respectively;is the aspect ratio of vertical tail;Λmaxtis the vertical tail sweep of string position of airfoil thickness;and η is the efficiency of airfoil.
Based on Assumption 1 and Definition 1,several geometric parameters in the case of vertical tail partial loss can be obtained.As shown in Fig.2,ctand crare the vertical tail tip chord length and the vertical tail root chord length respectively.The exposed area of vertical tail can be obtained as that in Eq.(3).

When the vertical tail damage degree is μ,the vertical tail tip chord length changes from ctto ct(μ);meanwhile,the height of vertical tail deduces by b(μ),also the aspect ratio of vertical tail changes into A(μ);considering all these factors,the nonlinear relationship between μ and Cyβcan be obtained based on trapezoid area equation.As shown in Fig.2,the lost area of vertical tail can be represented as

and therest area of the vertical tail should be
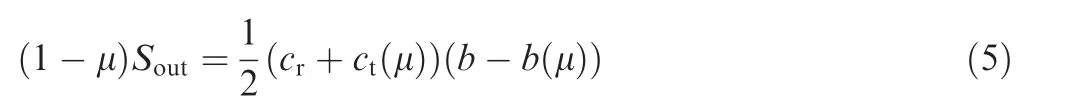
Combining Eqs.(3)and(4),b(μ)can be obtained as b(μ)=the n the effective rest vertical tail height can be represented as

Combining Eqs.(5)and(6),the representation of the vertical tail tip chord length can be obtained as


Fig.2 Regular damage and relative parameters of vertical tail loss.
Then the aspect ratio of vertical tail when the vertical tail suffers from μ degree damage can be obtained as

Finally the nonlinear relationship between μ and Cyβcan be obtained using the above equations as
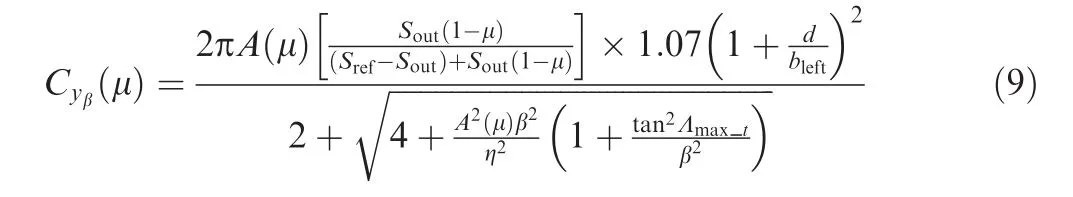
In order to simulate the nonlinear relationship between μ and Cyβ,this paper uses vertical tail characteristics of Boeing-747 and its corresponding parameters are chosen as:Sout=77 m2,Sref=87 m2,β=π/16,d=6.5 m,b=9.8 m,
The relationship between μ and Cyβis shown in Fig.3,in which Cyβdecreases gradually to 0 as μ changes from 0 to 1.In this process,the relationship between μ and Cyβpresents strong nonlinearity.The absolute difference|ΔCyβ|vs μ is shown in Fig.4,in which|ΔCyβ|reaches the maximum value when the damage degree μ=0.9.Based on this nonlinear function about μ and Cyβ,one more precise vertical tail damaged aircraft model can be obtained.

Fig.3 Function relationship between Cyβ and μ.

Fig.4 Absolute value difference of|ΔCyβ|vs μ.
2.1.2.Corresponding dimensional aerodynamic derivatives
In the case of aircraft suffering from vertical tail damage,there are also other damage-induced stability and control derivatives.Using Hitachi's research results,8the relationships between Cyβ(μ) and the rest corresponding derivatives can be obtained as

The nomenclature for all the parameters in Eq.(10)and the following Eq.(11)is the same as in Hitachi's research results.8Where Cnβ(μ) is the weathercock stability derivative;Clβ(μ) is the dihedral effect;Cyp(μ) is the side force-in-roll derivative,Cnp(μ) is the cross derivative of rolling-caused yawing moment;Clp(μ) is the damping-in-roll derivative;Cyr(μ) is the attack angle-caused derivative;Cnr(μ) is the damping-in-yaw derivative;Clr(μ) is the cross derivative of yawing-caused rolling moment;bwis the wing span;lvand zvare horizontal and vertical location of the aerodynamic center of the vertical tail;α is the attack angle of the zero lift line.
The affected stability and control derivatives indicate that the vertical tail damage would have significant impact on lateral and directional dynamic behavior.The corresponding changing aerodynamic derivatives in the lateral and directional dynamic model are listed as

where ρ is the air density;Swis the wing reference area.
2.2.Design of performance degradation input function
In this research,the civil aircraft with DRAS was studied.The structure of DRAS is shown in Fig.5,where uhand ueare the input signals for HA and EHA respectively,ivthe electrical signal for the servo valve,and θdthe deflection angle of the control surface.When the vertical tail suffers from serious damage,the vertical tail loss will pull apart the hydraulic pipelines,and the whole hydraulic system will lose pressure.In this case,all control surfaces actuated by HA system would be in loose floating state,and the n a catastrophic consequence may occur.Fortunately,if the new-type civil aircraft with DRAS can launch EHA to actuate some main control surfaces quickly,the aircraft can survive using this new type actuation system.
HA and EHA are different in response performance.EHA responds more slowly than HA.Therefore,the response performance degradation of EHA should be considered.In this section,the performance degradation input function was designed according to the transfer functions of HA and EHA.
2.2.1.Transfer function of HA and EHA
In the early research,25the force fighting problem of DRAS has been studied,similarly with the research work,the variable vector of DRAS was defined as

where xhand xeare cylinder piston displacement of HA and EHA respectively;vhand veare cylinder piston velocity of HA and EHA respectively;Phand Peare loading pressure of HA and EHA respectively;xvis the servo valve spool displacement of HA;and ωeis the motor speed of EHA.
Based on the research work,25the state space model of HA can be obtained as

where Bh,Beand Bdare equivalent damping parameter of hydraulic cylinder piston of HA and EHA,and the control surface respectively;mh,meand mdare equivalent mass of hydraulic cylinder piston of HA and EHA,and the control surface respectively;Ahis the area of HA hydraulic cylinder piston;Ehis the volumetric modulus of elasticity of HA;Vhis the total volume of the HA hydraulic cylinder;Kclis the sum of flow pressure and leakage coefficient of the HA hydraulic cylinder;Kqis the flow change coefficient;Kvis the proportionality coefficient of electro-hydraulic servo valve;τvis theservo valve time constant.
Using Laplace transformation,the transfer function of HA based on its state space model can be obtained as

where

The nomenclature for all the parameters in the equations above is the same as in the research work.25Then the dominant pole sH=aHwhich determines the response performance of HA can be obtained.
Still based on the research work,25the state space model of EHA can be obtained as

where Aeis the area of EHA hydraulic cylinder piston;Eeis the volumetric modulus of elasticity of EHA;Veis the total volume of EHA hydraulic cylinder;Celis the total leakage coefficient of EHA hydraulic cylinder;VPis the pump output of EHA;Jmis the total moment of inertia of motor and pump;Bmeis the simplified equivalent damping coefficient of the motor;Kmis the electromagnetic torque constant of the motor;Reis the is the armature resistance of the motor.

Fig.5 Dissimilar redundant actuation system composed of HA and EHA.
Using Laplace transformation,the transfer function of EHA based on its state space model can be obtained as

where

The nomenclature for all the parameters in the equations above is also the same as in the research work.25Then the dominant pole sE=aEwhich determines the response performance of EHA can be obtained.
2.2.2.Performance degradation input function
In order to compare the response performance of HA and EHA,a signal with the same step for HA and EHA was chosen to be used in simulation.As shown in Fig.6,EHA responds more slowly than HA.
From the transfer functions of HA and EHA,two dominant poles sH=aHand sE=aEwhich determine the response time of HA and EHA respectively can be obtained.Then the degradation performance parameter can be chosen as Δa=|aH-aE|,and the n the performance degradation input function can be obtained as

In this performance degradation input function,uHis the input of HA before the aircraft suffers from vertical tail loss,since the dynamics of actuator on control surface is much faster than the system dynamics,which means the control surface deflection bounded in the limit of amplitude can be considered equal to the command generalized by the controller without delay.However,when the aircraft suffers from vertical tail loss,only EHA provides effective measure for the aircraft to actuate the main control surfaces and the response performance degradation e-Δatshould be considered.

Fig.6 Response performance comparison of HA and EHA.
2.3.Accurate model of vertical tail damaged aircraft
When the aircraft suffers from vertical tail damage,the corresponding parameters and the input channel all change.Based on the analytical work in the above two sections,the final accurate damaged model can be obtained as

where the state variable vector is still x=[β, p, r, φ]T;d is the external disturbance,and the system matrices are changed into

where the elements of matrix A(μ) are calculated using the nonlinear damaged aircraft modeling method which is proposed in Section 2.1.The elements of the second column of matrix B(μ) change with the damage degree of the rudder,since the shape of the rudder is also regular trapezium which is proportional to the vertical tail,the damage rule is the same as the vertical tail.Therefore,a new damage coefficientwhich is also based on the fundamental equation Cyβ(μ),was constructed to obtain the damage matrix B(μ).The input channel was replaced by the performance degradation input function as shown in Eq.(19).

3.Fault-tolerant control strategy
The structure of the FTC strategy is shown in Fig.7.Under normal condition,the fault detection and isolation (FDI) mechanism would obtain healthy result of the aircraft,and the n the baseline control parameters would be solved by the LQR regulator.In this situation,HA systems actuate to maintain desirable flight attitude.Since this paper focuses on the development of AFTC strategy and there are many mature techniques to obtain the fault information,when the vertical tail of the aircraft suffers from partial loss,the damage degree can be assumed to be determined precisely by the FDI mechanism.The corresponding reconfigurable control law would be solved by the LQR regulator.Based on the information from FDI mechanism,the switch mechanism would change the baseline control law into reconfigurable one and launch EHA system for the fault-tolerance of the damaged aircraft.The design steps of the FTC strategy are shown in this section.
3.1.Baseline controller design
When all the control surfaces are in good condition,for the plant,a baseline controller was designed according to the following principles:The baseline controller should guarantee the stability of the whole closed loop system;the roll angle can track the given command rφ(t),the tracking error e(t)=rφ(t)- φ(t)→ 0;meanwhile,the sideslip angle β(t)→ 0°.
In order to satisfy the design principles,a closed loop feedback control law was designed in good condition as

The specific controller structure is shown in Fig.8.
If the control command was chosen as r=[rφ,rβ]Tand the plant output was chosen as y=[φ, β]T,the n their error e=r-y can be obtained.In order to eliminate the error,a control variable xc∈R2X1was introduced,and the control variable system should be˙xc=Acxc+Bc(r-y).Since the plant output is the controlled object variable vector and the plant follows the control command vector,the n the matrices of the control variable system can be chosen as Ac=0 and Bc=I.Finally an augmented system composed of the plant and the control variable system can be obtained as



where xaug=[x,xc]Tand uHis the input vector with HA;the optimal solution to minimize the total control cost can be obtained by solving the following Riccati Equation:

where the matrix P is positive and definite.Then the feedback gain Kxand Kccan be solved as

3.2.Reconfigurable controller design and adaptive parameter adjustment

Fig.8 Lateral-directional baseline control law.
When the aircraft suffers from vertical tail damage,the input channel of HA system would lose its ability to actuate;meanwhile,several stability derivatives change.In this situation,the baseline control law may not be robust enough to tolerate the fault to maintain a graceful flight performance,and may even threaten the flight safety.Therefore,another reconfigurable controller should be designed to stabilize the damaged aircraft model and realize required function reconfiguration.Since the severe loss of vertical tail occurs,the rudder would not continue to provide yaw function and the aileron's roll function can be used to provide the centripetal force to realize the yaw function finally.First,the reconfigurable control gain is resolved using LQR technique and the n MRAC method is used to adjust the solved control gain,which can guarantee that the reconfigurable control law is more effective.MRAC mechanism designed in this paper is shown in Fig.9.
The reference model can be expressed in the following form:



Since the plant and its reference model have the same dimension,model following method can be applied to designing the fault tolerant control strategy.
The error between the state of reference model Eq.(25)and plant Eq.(26)can be defined as eref=xm-xp,and the control input form was chosen as

where Keand Kmare control gain matrices which need to be solved and ΔUdis the input compensation which mainly deals with the outside interference d1in Eq.(26).

Fig.9 Mechanism of model reference adaptive control method.
Then the differential of state error can be written as

By choosing appropriate gain matrix Km∈ R2X6and ΔUdto satisfy the relationship described by Eq.(27),

it leads to

By checking the controllability of(Ap,Bp)and the poles of matrix Ap-BpKehave negative real part,the error eref=xm-xpcan be controlled to be zero.
The original feedback control gain matrices Keand Kmwere calculated through the plant matrices A(μ) and B(μ) in theory.ΔUdwas chosen following a certain adaptive adjustment law.Due to the parameter errors between the plant and the actual system,their closed loop dynamic performance may behave very differently.Adaptive parameter adjustment was used to realize the same dynamic performance,which leads the control law to be more efficient.
The adaptive parameter adjustment law is designed in the following process:

By defining Lyapunov function as


where Ke(0),Km(0)and ΔUd(0)are the initial values;Ke(t),Km(t)and ΔUd(t)are the current moment value obtained through the designed adaptive law.
4.Simulation study
4.1.Flight conditions and data
To verify the modeling and the effectiveness of the proposed method in this paper,it was used on the Boeing 747 lateraldirectional model.The given model is in steady flight of certain flight condition.The data are listed in Table 1.10
4.2.Simulation results
4.2.1.Simulation for effectiveness of baseline control law
First,the baseline control law parameters was solved using the proposed fault-tolerant strategy and LQR technique,and the n its effectiveness was verified in normal conditions.The specific expressions for system coefficients A and B were given as

The baseline control law parameter matrix was solved as Kbase(0)

Fig.10 shows the system dynamic performance in normal conditions.As shown in Fig.10(a),a sine wave signal with peak value of±12°was given to the model as the roll command.The roll angel response can track the command well with acceptable time delay,meanwhile,the fluctuation amplitude of the sideslip angel is limited in ±0.1°and can be regarded as zero steady state.

Table 1 Flight condition,aircraft parameters and derivatives.

Fig.10 System dynamic performance in normal condition.
As shown in Fig.10(b),when given a step signal of 12°during 10–20 s and 40–50 s as the roll command,during the control process,the roll response curve can track the command well and the sideslip angle can steady at zero value finally.
The above simulation results illustrate the effectiveness of the baseline control law design.
4.2.2.Simulation for comparisons between modeling and faulttolerant control methods
In this section,three methods were chosen to compare with each other to illustrate the control improvement of the nonlinear modeling method and the effectiveness of the proposed AFTC method.Notations for the three methods were made as follows.
Method 1(M1):PFTC method (guaranteed cost control with robust pole placement) with linear modeling for the damaged aircraft model in Ref.10.
Method 2(M2):AFTC method (MRAC composed with LQR regulator) with linear modeling for the damaged aircraft model.
Method 3(M3):AFTC method (MRAC composed with LQR regulator) with nonlinear accurate modeling for the damaged aircraft proposed in this paper.
The absolute difference|ΔCyβ|reaches the maximum value when the damage degree μ=0.9,it means the modeling error also reaches the maximum value,therefore,the linear and nonlinear modeling methods were compared at μ=0.9.
The system coefficient matrices using linear modeling method were obtained as

It has been proved that M1has obvious effectiveness when the damage degree is not very serious.10In this paper the damage degree μ=0.9 was chosen to verify the control result of the PFTC method compared with the AFTC ones.LMI constraint conditions in Ref.10were solved to obtain the control parameter matrix of M1as

The initial control parameter matrix of M2was solved using LQR regulator as

The system coefficient matrices using the proposed nonlinear modeling method were obtained as

The initial corresponding fault tolerant control parameter matrix of M3was solved as

In this section,a sine wave signal and a step signal were used in simulations and the control results of M1,M2and M3were compared with each other.Fig.11 shows the system dynamics performance comparison between PFTC and AFTC methods.The analysis for the simulation results are as follows.

Fig.11 System dynamics performance using PFTC and AFTC with μ=0.9.
When giving the damaged model a sine wave signal,the output responses using M1,M2and M3are shown in Fig.11(a).First,the control results of M1and M2were compared:using M1to control the damaged model,the roll angle can hardly track the command signal and diverge to extremely serious degree,meanwhile,the sideslip angle also presents divergent trend.Air crash would happen in this situation.Simulation results illustrate that it is futile to use M1to control the damaged model to serious damage degree,and the aircraft would crash due to extreme rolling act.Compared with M1,when using M2,though time delay exists,the roll response can track the command with small sideslip angle mostly.It illustrates that when the damage degree is serious to some certain extent,AFTC method is more efficient and can avoid air crash.Second,the control results of M2and M3were com-pared:compared with M2,though the fluctuation amplitude in sideslip response is a little bigger,it is very small and acceptable.Meanwhile,the time delay of tracking performance is obviously shorter since Δt2gt;2Δt1;besides,using M3can eliminate the wave error Δd.This comparison illustrates that based on the proposed nonlinear accurate modeling model,the control performance for the damaged aircraft model can be improved.
The roll command signal was chosen in the form of steps during 10–20 s and 40–50 s.The output responses using M1,M2and M3are all shown in Fig.11(b).First,the control results of M1and M2were compared:similarly to the sine wave signal condition,using M1to control the damaged model,the roll angle can hardly track the command signal and diverge to extremely serious degree;meanwhile,the sideslip angel also presents divergent trend.Simulation results illustrate that it is futile to use M1to control the damaged model when μ=0.9,the aircraft would crash due to extreme rolling act.Compared with M1,when using M2,the sideslip angle can stabilize near zero value and the roll response does not diverge;however,the tracking performance is still very bad.This comparison illustrates that when the damage degree is serious to some certain extent,AFTC method is very necessary.Second,the control results of M2and M3were compared:compared with M2,though there exist fluctuations in sideslip response,the fluctuation amplitude and the frequency are very small and acceptable;meanwhile,the tracking performance of the roll angle is obviously better than that using M2.This comparison illustrates that based on the proposed nonlinear accurate modeling model,the control performance for the damaged aircraft model can be improved.
4.2.3.Simulation for effectiveness of AFTC method in maximum damage condition
In this section,the control effectiveness of the proposed AFTC method in maximum damage condition was verified.The damage degree was chosen as μ=1.0,which means the aircraft totally lose the whole vertical tail.The damaged model matrices and the control law matrix were calculated as damaged model,the roll angle response can track the command well with acceptable time delay;meanwhile,though the sideslip angle response has sine wave fluctuation,the fluctuation amplitude is limited to be±0.1°and can be regarded as zero steady state.

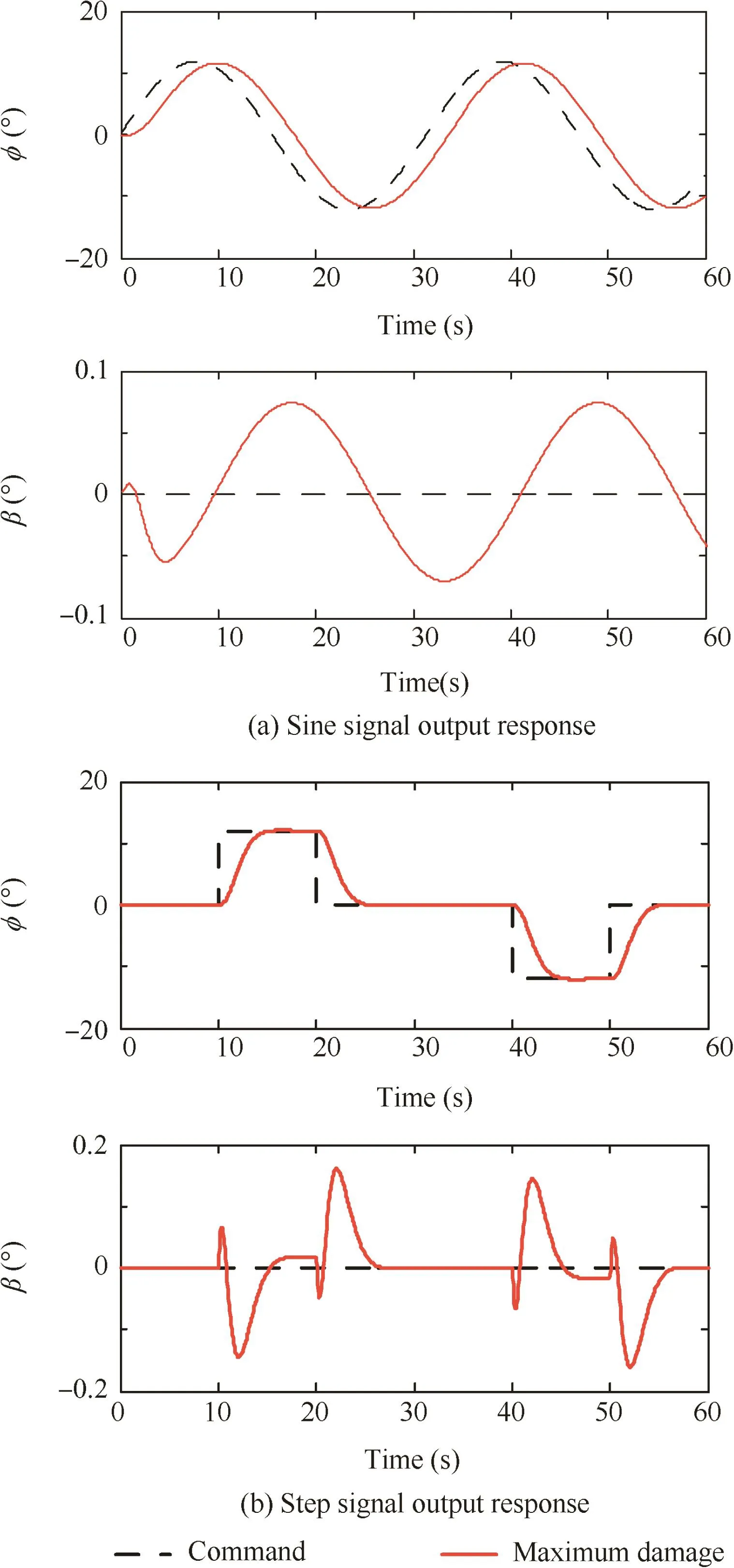
Fig.12 System dynamic performance under AFTC control law in maximum damage condition.
As shown in Fig.12(b),when the vertical tail damage degree μ =1.0,using the AFTC method,a step signal of 12°during 10–20 s and 40–50 s was given to the damaged model as the roll command,the roll angle response can track the

Fig.12 shows the system dynamic performance under AFTC control law in maximum damage condition.As shown in Fig.12(a),when the vertical tail damage degree μ=1.0,using the AFTC method,a sine wave signal was given to the command well;meanwhile,though the sideslip angle response has higher fluctuation frequency than before,the fluctuation amplitude is limited to be±0.2°and finally stabilized at zero value.
The simulation results shown in Fig.12 illustrate that even in the most serious damage degree,the proposed AFTC method can maintain the damaged aircraft controllable and safe.
5.Conclusions
In this paper,the modeling and control of new-type civil aircraft under vertical tail damage condition have been studied and evaluated.
(1)The fault tolerant control capability of aircrafts with DRAS to respond to extraordinary situations is discussed.A damage degree coefficient based on the effective vertical tail area is introduced,and the n the nonlinear relationship between the damage degree and its relevant stability and control derivatives are studied.Meanwhile,the performance of EHA is also modeled in the damaged dynamic model.Considering these two factors,an accurate damaged dynamic model is developed.
(2)The fault tolerant control strategy for the damaged aircraft model with vertical tail loss is studied.Based on the accurate modeling,the fault tolerant strategy,using MRAC composed with LQR technique,is developed.In this way,the control law parameters can be determined by LQR method more efficiently and can be adjusted using MRAC to be more precise in fault condition.Simulation results to different damage degrees indicate the effectiveness of the fault tolerant control strategy.
(3)Our further research will focus on the problem of fault degree detection and isolation,and the n integrate the FDI technique with the fault tolerant strategy efficiently.Based on this comprehensive technology,our fault tolerant strategies may be more applicable.
Acknowledgements
This work was supported by the National Basic Research Program of China(No 2014CB046402),the National Natural Science Foundation of China(No.51575019)and 111 Project of China.
1.Crider LD.Control of commercial aircraft with vertical tail loss.Proceedings of AIAA 4th aviation technology,integration,and operation (ATIO) forum.2004 Sep 20–24;Chicago,lllinois.Reston:AIAA;2004.
2.Boskovic JD,Prasanth R,Mehra RK.Retrofit fault-tolerant flight control design under control effector damage.J Guid Control Dynam 2007;30(3):703–12.
3.Edwards C,Lombaerts T,Smaili H.Fault tolerant flight control.Lect Notes Contr Inform Sci 2010;399:21–45.
4.Wang J,Li Z,Peng B.Modeling and analysis of the dissimilar redundant actuator system.Mach Tool Hydraul 2008;36(6):79–81.
5.Fu Y,Pang Y.Design and working mode analysis of dissimilar redundant actuator system.J Beijing Univ Aeronaut Astronaut 2012;38(4):432–7[Chinese].
6.Karam W,Mare J.Force control of a rollerscrew electromechanical actuator for dynamic loading of aerospace actuators.International conference on fluid power and motion control.2008 Jun 21–27;Darmstadt.Bellingham:ASME;2008.p.515–28.
7.Shah GH.Aerodynamic effects and modeling of damage to transport aircraft.Proceedings of AIAA atmospheric flight mechanics conference and exhibit.2008 Aug 18–21;Honolulu,Hawaii.Reston:AIAA;2008.
8.Hitachi Y.Damage-tolerant flight control system design for propulsion-controlled aircraft[dissertation].Toronto:University of Toronto;2009.
9.Zhao J,Jiang B,Shi P,He Z.Fault tolerant control for damaged aircraft based on sliding mode control scheme.Int J Innovative Comput Inf Contr 2014;10(1):293–302.
10.Li X,Liu HHT.A passive fault tolerant flight control for maximum allowable vertical tail damaged aircraft.J Dynam Syst Meas Contr 2012;134(3):1625–32.
11.Zhang Y,Jiang J.Activefault-tolerant control system against partial actuator failures.IEE Proc-Contr Theory Appl 2002;149(1):95–104.
12.Zhang Y,Jiang J.Integrated active fault-tolerant control using IMM approach.IEEE Trans Aerosp Electron Syst 2001;37(4):1221–35.
13.Ye D,Yang GH.Adaptive fault-tolerant tracking control against actuator faults with application to flight control.IEEE Trans Contr Syst Technol 2006;14(6):1088–96.
14.Cieslak J,Henry D,Zolghadri A,Goupil P.Development of an active fault-tolerant flight control strategy.J Guid Contr Dynam 2008;31(1):135–47.
15.Maki M,Jiang J,Hagino K.A stability guaranteed active faulttolerant control system against actuator failures.Int J Robust Nonlinear Contr 2004;14(12):1061–77.
16.LiYX,Yang GH.Adaptive fuzzy decentralized control for a class of large-scale nonlinear systems with actuator faults and unknown dead zones.IEEE Trans Syst Man Cybern:Syst 2016;99:1–12.
17.Li YX,Yang GH.Robust fuzzy adaptive fault-tolerant control for a class of nonlinear systems with mismatched uncertainties and actuator faults.Nonlinear Dynam 2015;81(1–2):395–409.
18.Stengel RF,Huang CY.Restructurable control using proportional-integral implicit model following.J Guid Contr Dynam 1990;13(2):303–9.
19.Bodson M,Groszkiewicz JE.Multivariable adaptive algorithms for reconfigurable flight control.IEEE Trans Contr Syst Technol 1997;5(2):217–29.
20.Bosˇkovic JD,Mehra RK.Intelligent adaptive control of a tailless advanced fighter aircraft under wing damage.J Guid Contr Dynam 2000;23(5):876–84.
21.Lavretsky E.Combined/composite model reference adaptive control.IEEE Trans Autom Contr 2009;54(11):2692–7.
22.Terra MH,Cerri JP,Ishihara JY.Optimal robust linear quadratic regulator for systems subject to uncertainties.IEEE Trans Autom Contr 2014;59(9):2586–91.
23.Chen C.On the robustness of the linear quadratic regulator via perturbation analysis of the Riccati equation [dissertation].Dublin:Dublin City University;2015.
24.Etkin B,Reid LD.Dynamics of flight:Stability and control.New York:Wiley;1996.p.93–114.
25.Shi C,Wang X,Wang S,Wang J,Tomovic MM.Adaptive decoupling synchronous control of dissimilar redundant actuation system for large civil aircraft.Aerosp Sci Technol 2015;47:114–24.
Wang Junis a Ph.D.candidate at School of Automation Science and Electrical Engineering,Beihang University,Beijing,China.He received the B.S.degree in mathematics and applied mathematics from Shandong Normal University,Ji'nan,China,in 2011;and the n he received the M.S.degree in mathematics from University of Science and Technology Beijing,Beijing,China,in 2014.His main research interests are fault diagnostic and fault tolerant control.
Wang Shaopingreceived the Ph.D.,M.E.and B.E.degrees in mechatronics engineering from Beihang University,Beijing,China,in 1994,1991 and 1988.She has been with the Automation Science and Electrical Engineering at Beihang University since 1994 and promoted to the rank of professor in 2000.Her research interests are engineering reliability,fault diagnostic,prognostic and health management,as well as active fault tolerant control.
Wang Xingjianreceived the Ph.D.and B.E.degrees in mechatronics engineering from Beihang University,Beijing,China,in 2012 and 2006.From 2009 to 2010,he was a visiting scholar in the School of Mechanical Engineering,Purdue University,West Lafayette,IN,U.S.He is currently with the School of Automation Science and Electrical Engineering,Beihang University,Beijing,China.His research interests are nonlinear control,active fault tolerant control,fault diagnostic and fault prognostic.
Shi Cunis a Ph.D.candidate at School of Automation Science and Electrical Engineering,Beihang University,Beijing,China.He received the B.E.degree in Mechanical Engineering from China Agricultural University,Beijing,China,in 2014.His main research interests are prognostic and health management and fault tolerant control.
Mileta M.Tomovicreceived the Ph.D.,M.S.and B.S.degrees in mechanical engineering from University of Michigan,Massachusetts Institute of Technology,University of Belgrade,in 1991,1981 and 1979 respectively.He has been with the mechanical engineering technology department at Purdue University from 1991 to 2008 and served as Chair of Engineering Technology Department in Old Dominion University since 2008.His research interests include design,manufacturing systems and processes,product lifecycle management,system dynamics and control.
13 October 2015;revised 28 March 2016;accepted 13 May 2016
Available online 27 August 2016
Dissimilar redundant actuation system;
Electro-hydrostatic actuator;
Fault-tolerant control;
Linear quadratic regulator;
Model reference adaptive control;
Nonlinear aircraft model;
Vertical tail loss
©2016 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).
*Corresponding author.Tel.:+86 10 82338917.
E-mail addresses:dwill-wang@buaa.edu.cn(J.Wang),shaopingwang@vip.sina.com(S.Wang),wangxj@buaa.edu.cn(X.Wang),shicun@buaa.edu.cn(C.Shi),mtomovic@odu.edu(M.M.Tomovic).Peer review under responsibility of Editorial Committee of CJA.
杂志排行
CHINESE JOURNAL OF AERONAUTICS的其它文章
- Design and experimental performance verification of a thermal property test-bed for lunar drilling exploration
- Dependence of creep age formability on initial temper of an Al-Zn-Mg-Cu alloy
- Plastic deformation analysis and forming quality prediction of tube NC bending
- Tool wear during high speed turning in situ TiCp/TiBwhybrid reinforced Ti-6Al-4V matrix composite
- Comparative investigation on high-speed grinding of TiCp/Ti–6Al–4V particulate reinforced titanium matrix composites with single-layer electroplated and brazed CBN wheels
- High-cycle fatigue behavior of Co-based superalloy 9CrCo at elevated temperatures
