数学娱乐(十七)——黎族数字

耿 济

(海南大学，海南 海口 570228)



数学娱乐(十七)
——黎族数字

耿 济

(海南大学，海南 海口 570228)

黎族； 甲骨文； 数字

本文是数学娱乐文献[1-16]续作.

1932年至1933年田曙岚环游海南岛，历程1 500余公里，考察自然生态与社会风貌，写成《海南岛旅行记》一书出版，风行一时畅销全国.2011年王春煜教授认为该书文化含量高，深具历史价值，对原著认真校勘，增加海南老照片，《海南岛旅行记》新版问世，为海南的文化与历史作出贡献.

海南岛是黎族世居的地方，距今2 800年前从华南沿海一带横渡琼州海峡而来.目前全岛黎族人口130多万人，占全国黎族人口90%，因此该书有关黎族的内容引起笔者的重视.

本文根据该书新版中“感恩(今东方)黎人的风俗”的“賒刻为契，刳两执之”[17]，从黎族数字谈起，说明黎族文字处于萌芽状态.

1 黎族数字与应用

黎族数字中的1，10，100，1 000依次写成

2，20，200，2 000依次写成

3，30，300，3 000依次写成

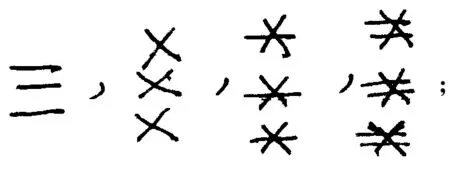
如此类推，直到9，90，900，9 000为止(从略).

对于10 000以内的任意正整数的写法，以1234为例，把1 000，200，30，4依次相加合成就有

黎族数字具有左、右对称的特性，这一特性应用在借贷时极为重要.

当甲方与乙方发生借贷关系时，双方同意邀请一位德高望重的为公证人，在竹片或木片上用刀刻着借贷的数字，一劈为二，双方各持一片保存.当债务还清后，同时把双方的竹片或木片烧毁(如果先还部分债金时，双方请出公证人用刀在双方所持的竹片或木片上削去所还的债金后，仍交给各方保存，直到还清为止).

2 黎族数字与甲骨文相同的数字

甲骨文是我国商殷时代契刻在龟甲或兽骨上的古老文字，最早发现的地方是河南安阳市小屯村，现在国内外收藏的甲骨有十五万片之多，其中有的与数学有关，甲骨文中有一，十，百，千，万的数字，最大的是三万，大于十的数字是十进位值制记数法，著名数学家吴文俊指出这一创造“可以与火药、指南针、印刷术一类发明相媲美”.

现在介绍天津文物管理处收藏的一片珍贵的甲骨，如图1所示.

卜辞内容：壬子卜，亘贞至于丙辰雨；一、二、三、四、五、六、七、八、九，上告.拓片卜辞对照图，如图2所示.

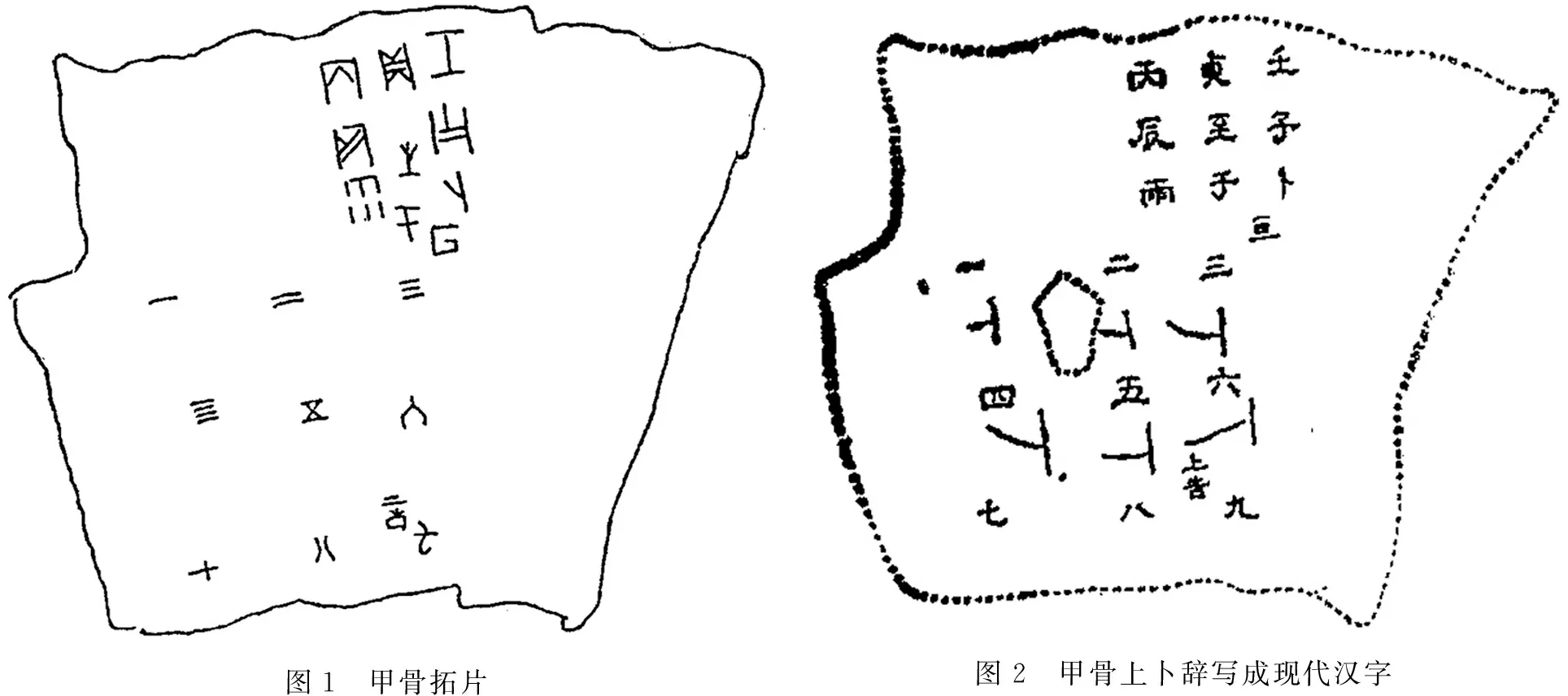
图1 甲骨拓片图2 甲骨上卜辞写成现代汉字

通过图1与图2得出从一至九的对照表.

表1 现代汉字与甲骨文一至九的对照

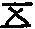
林东辅著《龟甲兽骨文字》卷一第十八页第十三片，如图3所示.

图3 甲骨拓片 图4 甲骨拓片

陈邦福著《殷墟甲骨余拓录》第十片，如图4所示.

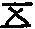
现有两见，并非单字孤文.

3 黎族文字处于萌芽状态

通过下面文献资料结合海南岛黎族实际说明黎族文字处于萌芽状态.

古代名著《易·系辞传》记载“上古结绳而治，后世圣人易之以书契.”

三国吴虞翮翻著《易九家义》指出“事大，大其绳；事小，小其绳，结之多少，随物众寡”.

近代于省吾著《甲骨文字释林》指出“我国古文字，当自纪数字开始，纪数字乃古文字中之原始字，……，由一至四均为积画.”

综上所述，上古时代人们“结绳而治”，应用绳子结扣来记事和记数，重大的事情就把绳子打一个大结扣，小的事情就把绳子打一个小结扣；绳上结扣的多少，反映出事物的数量多少.后世的圣人发明文字，开始用文字记事和记数，最早的文字是数字，正如甲骨文中一字一画，二字二画，三字三画，四字四画，这是最原始的文字.

海南岛黎族社会里出现过“结绳而治”，也出现过记数的数字，这些数字正是最原始的文字，由于历史的原因，长期处于文字的萌芽状态.

最近蔡宁著《破译黎族“文字”的密码》一文指出：“黎族作为海南岛上最早的原住民，他们依靠自己智慧和与大自然长期和谐相处中积累起丰富的生活经验知识，造就了本民族独特的文化形态——黎锦、黎药、白制陶、独木器等，黎族在海南岛居住生活的几千年历程中，同样也有自己的类文字载体：刻本记事和刻画……，是一个融合了黎族生活记事、婚恋、信仰等含义的特殊文字符号，从远古至今天黎族所使用的一个个器件中，折射出黎族‘文字’变化的历程”[19].

从数学的观点来看自然数，人们在绳上打一个结扣，从一开始，接着再打一个结扣，通过一加一得到二；又打一个结扣，通过二加一得到三；如此继续累加起来，黎族数字从一至九明显地出现积画的过程，甲骨文也存在积画的过程，随着文字的发展逐步被淘汰，直至现在的汉字中的一、二、三依然保留着残留着积画的痕迹.

[1] 耿济.数学娱乐(一)——夫妻问题的新证与应用[J].海南大学学报(自然科学版)，2007，25(4)：321-324.

[2] 耿济.数学娱乐(二)——牙牌问题的新证与推广[J].海南大学学报(自然科学版)，2008，26(3)：206-219.

[3] 耿济.数学娱乐(三)——洛书定理与应用[J].海南大学学报(自然科学版)，2008，26(4)：303-308.

[4] 耿济.数学娱乐(四)——Nasik幻方的性质与构造法[J].海南大学学报(自然科学版)，2009，27(2)：107-115.

[5] 耿济.数学娱乐(五)——推广Fibonacci数列与幂级和[J].海南大学学报(自然科学版)，2009，27(4)：313-319.

[6] 耿济.数学娱乐(六)——黎棋相间[J].海南大学学报(自然科学版)，2010，28(1)：1-10，14.

[7] 耿济.数学娱乐(七)——一个麻将和牌问题[J].海南大学学报(自然科学版)，2010，28(2)：93-98.

[8] 耿济.数学娱乐(八)——易经卦象的起源与考古发现的奇字[J].海南大学学报(自然科学版)，2011，29(2)：99-103.

[9] 耿济.数学娱乐(九)——学习《九章算术》的收获[J].海南大学学报(自然科学版)，2011，29(4)：297-304.

[10] 耿济.数学娱乐(十)——学习《九章算术》的收获[J].海南大学学报(自然科学版)，2010，30(2)：95-102.

[11] 耿济.数学娱乐(十一)——幻方与线性代数[J].海南大学学报(自然科学版)，2012，30(4)：299-305.

[12] 耿济.数学娱乐(十二)——广义华林公式与应用[J].海南大学学报(自然科学版)，2013，31(1)：1-7.

[13] 耿济.数学娱乐(十三)——类似华林公式的新公式[J].海南大学学报(自然科学版)，2013，31(2)：93-99.

[14] 耿济.数学娱乐(十四)——圆组合新概念与圆组合恒等式[J].海南大学学报(自然科学版)，2014，32(1)：1-7.

[15] 耿济.数学娱乐(十五)——从三角函数公式到伯努利数和欧拉数[J].海南大学学报(自然科学版)，2014，32(4)：295-301.

[16] 耿济.数学娱乐(十六)——移棋相间问题与国际科研成果[J].海南大学学报(自然科学版)，2015，33(3)：197-203.

[17] 田曙岚.海南岛旅行记(新版)[M].海口：海南出版有限公司，2011，111.

[18] 耿济.甲骨文中“五”字初文的探讨[J].海南大学报(社会科学版)，1989，22(1)：102-106.

[19] 蔡宁.破译黎族“文字”的密码[N].海南日报海南周刊，2015-11-16(819).

Mathematical Recreation (XVII): Li Nationality Numerals

Geng Ji

(Hainan University,Haikou 570228,China)

Li nationality; inscriptions on bones or tortoise shells of the Shang Dynasty; number

2015-10-12

耿济(1929-)，男，江苏镇江人，海南大学(退休)教授.

1004-1729(2016)03-0199-04

O 1

A DOl：10.15886/j.cnki.hdxbzkb.2016.0030