一种改进的DV-HOP算法在无线传感网中的定位研究

陈玲君

（绍兴职业技术学院，浙江绍兴　312000）

一种改进的DV-HOP算法在无线传感网中的定位研究

陈玲君

（绍兴职业技术学院，浙江绍兴312000）

WSN中的信息传递主要通过传感器来进行传递信号，针对无线传感中DV-Hop算法在节点定位上存在精度低的问题，首先提出建立双曲线二维模型用来确定锚节点与未知节点的距离关系，其次设定误差系数使得传感器节点之间的误差降低，最后采用斯蒂芬森迭代法（Steffensen）定位方法对传感器节点进一步进行定位修正；仿真实验表明算法的在远程控制的中定位精度提高，传感器之间能量消耗降低，具有一定的推广价值。

无线传感网络；双曲线二维模型；误差系数；斯蒂芬森

0　引言

伴随着微电子技术和计算无线通信技术的发展，无线传感网络 （wireless sensor network，WSN）得到了迅速的发展。传感器之间的信息传递主要依赖于节点位置的分布，因此节点的准确定位是目前研究的主要的问题［1］。WSN中的节点定位主要是指锚节点定位和未知节点定位，其中锚节点是指少量的带有GPS定位装置的节点，未知传感器节点位置的定位需要通过锚节点来进行自身的定位。国内外学者对于DV-HOP算法进行了广泛的研究，文献［2－3］提出采用智能算法来对DV-Hop的定位结果进行了优化具有很好的稳定性；文献［4］提出一种基于加权的三维DV-Hop定位算法，该算法降低定位误差，但是权值的设置需要进一步讨论；文献［5］提出了将接收信号强度指示的改进算法，降低了误差30%～45%；文献［6］提出根据邻居节点间的距离对跳数进行加权处理，修正平均跳距，缩小未知节点被包围的三角形区域，筛选出最终进行坐标计算的锚节点，其缺点是区域的设置受到其他条件的影响；文献［7］提出了一种普适性反馈机制，引入位置调整因子和基于RSSI的跳距优化算法，实验表明，在资源变化的网络计算环境中，所提出的定位算法能够显著地提高定位精度，且具有更强的稳定性；文献［8］提出了对DV-Hop算法中的平均跳距值进行调整，使得锚节点与未知节点之间的距离误差变小，缺点是实际环境难以应用；文献［9］提出了一种综合考虑所有信标节点的平均跳距并引入权值修正，该算法使得网络平均跳距和节点位置估计值更加准确。文献［10］提出从锚节点组合的有效性和节点早定位能减少因等待锚节点信息所耗的时间和能量两方面考虑，并进行改进，仿真实验表明算法效果良好。

为了进一步提高传感器定位的精度，本文在DV-HOP算法的基础上引入斯蒂芬森迭代法（Steffensen）对传感器节点定位进行修正。分析DV-Hop算法存在的不足，建立双曲线二维方程，通过设定误差系数降低偏差，采用Steffensen迭代法对DV-Hop算法定位结果进行检验和修正，仿真实验表明本文的算法能够有效的提高定位性能。

1　DV-Hop算法及误差分析

1.1DV-Hop定位算法

DV-Hop算法的具体步骤如下：

1）锚节点向周围的节点广播数据包，未知节点收到锚节点的最小跳数，进行加1后转发给下一个节点。

2）锚节点收到其他节点的信息和跳数后，计算平均每跳的距离进行估算，按照公式（1）。

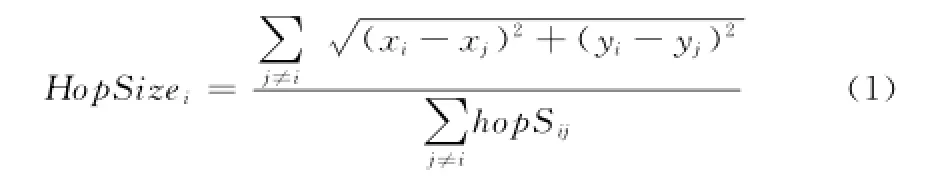
式中，分别是锚节点i和j的坐标，hop Sij是两个锚节点i和j间的最小跳数。

3）锚节点与未知节点之间估计距离为：

Li=Si×Hop Size（2）

根据未知节点与各锚节点间的距离，采用多边法计算未知节点的坐标，具体为：

式中，（xi，yi）为未知节点的坐标；（x1，y1），（x2，y2），…（xj，yj）为该未知节点所记录锚节点的坐标。因此未知节点（xi，yi）通过公式（4）得到1.2误差分析在DV-HOP算法中主要采用锚节点之间的距离来近似估算未知节点到锚节点之间的距离，但具有一定的局限性，主要是因为取决于锚节点是否分布均匀，但实际情况恰恰相反，锚节点的定位受到很多因素的影响，当网络中的锚节点之间分布密集的时候，网络中的未知节点之间的距离接近于实际距离，但当锚节点分布稀疏的时候，偏差就容易产生，如图1所示。

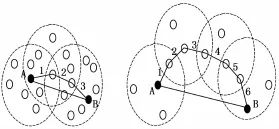
图1　节点分布造成的误差

因此DV-Hop算法测量所得到距离L与实际距离之间必然存在一定误差，假设fn为未知节点到锚节点之间的测距误差系数，则未知节点到锚节点的距离为公式（5）所示（xi-xj）2+（yi-yj）2=L2j+fj（5）根据公式（3）得到未知节点坐标满足下式：

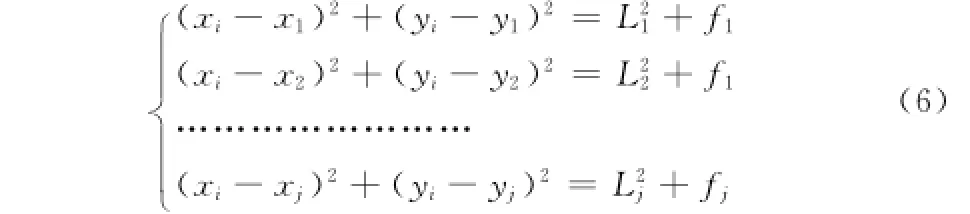
求解未知节点坐标（xi，yi），使得

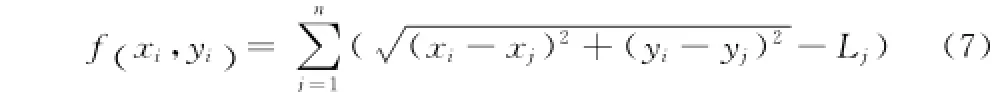
当（7）式取得最小值时，总误差最小，未知节点的定位就能接近真实值。即满足下式的未知节点坐标：

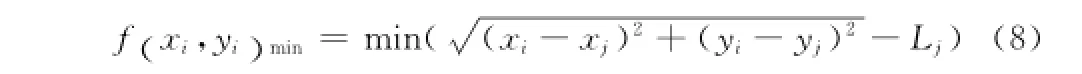
通过上述方式把DV-Hop定位误差问题成功地转化一个非线性优化问题，通过斯蒂芬森迭代法对式（8）进行求解，进一步优化传感器定位精度。

2　WSN中的改进的DV-Hop算法

2.1基于双曲线的二维平面

为了降低研究的复杂度，本文选择在二维平面作为研究对象，假设在有M个传感器节点，第i个未知节点坐标为Mi，j =［xi，yi］T（i=1，2，…，n，j=1，2，……，n），锚节点的坐标为Sp=［a，b］T，因此每一个节点发送源与传感器之间的距离为||Mi-Sp||。以选取其中第j个未知节点作为参考节点，通过观测值κi，j（i=1，……N）用来表示在锚节点与未知节点之间的关联关系，设定关于锚节点与未知节点之间的关系为双曲线方程，如图2所示。

图2　WSN中的双曲线定位

设定信号之间的传播速度为v，则锚节点与未知节点之间的距离为d=vκi，j，构建以锚节点为中心的构建N个双曲线方程di，j=di-dj，通过对N个方程求解得到定位的节点坐标。由于该方程式非线性方程，所以，需要对其进行线性处理，由d2i=（di，j+dj）2进行拓展得到如下：

d2i，j+2di，jdj+3d2i=M2i，j+Sp-2SMi，j（9）对公式（9）进行局部处理，得到公式（10）

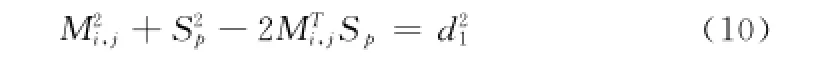
将公式（10）带入公式（9）得到如下：

M2i，j-S2p-2（Mi，j-M1，1）TSp=d2i，j+2di，jdj（11）通过公式（11），将问题转换为线性方程的求解，代入（8）进行求解。

2.2误差系数设定

由于锚节点与未知节点的实际距离与理论距离肯定存在误差，因此通过设定误差系数来减少，之前描述了未知节点与锚节点之间的实际距离为Di，j，

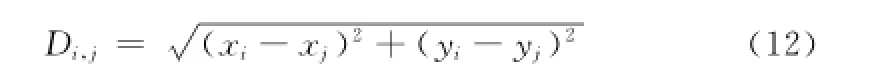
根据公式 （12）和公式 （3）得到未知节点到锚节点之间的总误差ε，如公式（13），误差系数的确定如公式（14）

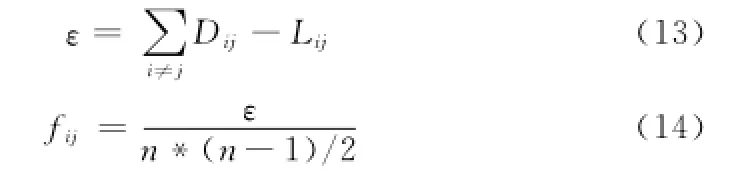
式 （14），n*（n-1）/2表示n个节点之间的跳数总和，fij表示误差系数

2.3Steffensen算法

对于非线性方程f（x）=0，可化成等价的方程：x=φ（x）（15）式中，φ（x）称为迭代函数。

Steffensen迭代法是一种改进的不动点迭代法，具有二阶收敛速度、计算精度等优点，迭代函数为：

Steffensen迭代公式为：

Steffensen算法流程如下：

1）设置最大迭代次数N和精度ε，令k=0。

2）计算yk=φ（xk），zk=φ（yk），。

4）若k=N，则停止计算；否则，置k=k+1，转到步骤2）。

2.4Steffensen修正DV-Hop定位误差

除了对误差系数进行设定之外，还需要（8）取得最小值的必要条件是：

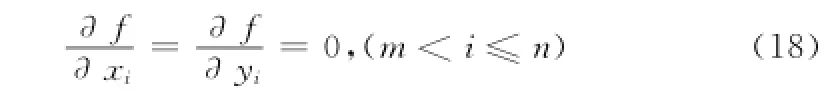
其中：

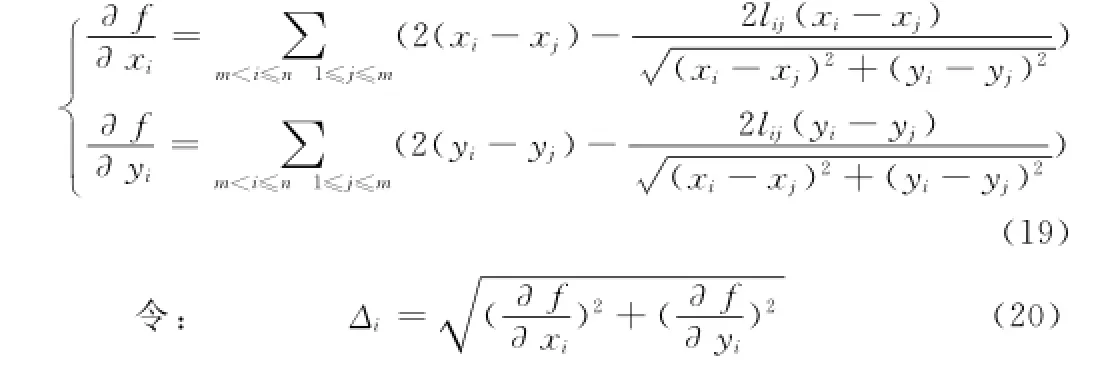
则求min（fitness（））的最优解问题转化为求使得Δi取到最小值时未知节点的坐标（xi，yi）的问题。具体步骤为：

1）按照Steffensen迭代公式（17）的第一步，对变量xi和yi进行迭代，有：

式中，xi和yi为采用DV-Hop算法的传感器节点估计位置，将其作为迭代初值。

2）根据式（17）对未知节点坐标进行更新迭代操作：

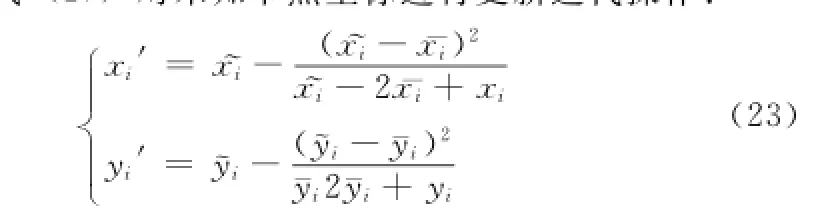
3）将新的未知传感器节点的坐标（xi，yi）代入式（20）中，算出Δi的值。

4）当迭代次数达到所设的最大值，迭代算法停止，求出最接近真实值的未知节点的坐标，使得定位误差最小。

3　算法仿真与分析

进行仿真实验的硬件选择CPU为酷睿i3，4GDDR3和硬盘为500 G，软件采用matlab2012。采用本文算法与基本DVHOP算法以及文献［2］算法进行比较。选择100 m*100 m的区域，选择1000个节点，其中220个为锚节点，780为未知节点，所有节点都进行随机分布。采用误差计算公式（24）作为比较的标准，其中（x′i，y′i）和（xi，yi）分别表示估算未知和实际未知，R为节点通信半径，N为节点个数，结果如下

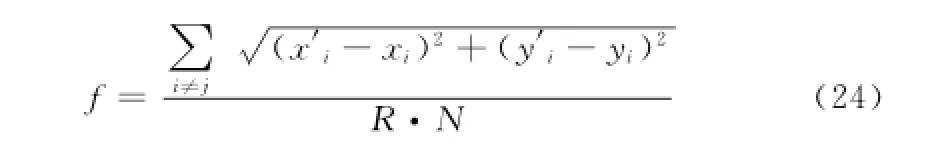
图3表示在不同的节点密度与定位误差关系。从图中发现3种算法伴随着节点密度的增大都对定位误差进行了优化，从中发现本文算法所产生的误差是的最小，相比与DV-HOP算法平均优化了21.2%，相比与文献［2］算法优化了7.23%，这说明本文算法能够获得更精确的定位结果。

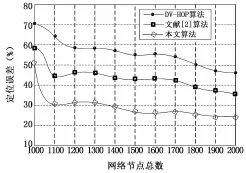
图3　节点密度对定位误差的影响

图4表示在不同的节点通信半径与定位误差的关系。节点通信半径关系到未知节点定位准确性，选择节点半径从5到15米的范围，从图中可以发现3种算法定位误差都伴随着节点通信半径不断增大而减少，这说明3种算法都的改进都改善了与节点通信半径之间的关系，本文算法曲线平缓，说明节点半径的增大不影响算法的稳定性，因此本文算法的的定位误差相比与其他两种算法能够更好的完成更精确定位。

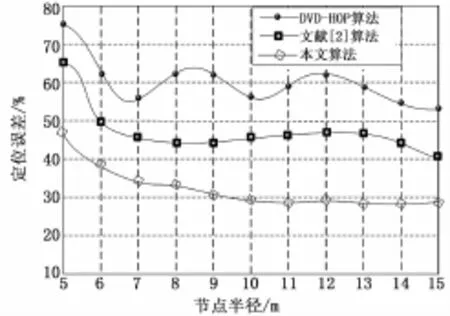
图4　节点通信半径对定位误差的影响

图5表示锚节点比例与定位误差的关系。3种算法中锚节点的比例按照2%到20%的顺序增加，从图中发现本文的算法相比于其他两种算法在锚节点比例不断增大的情况下，定位误差相比与DV-HOP算法降低了12.3%，相比与文献［2］算法降低了5.2%，这说明锚节点的数量增多的情况，本文算法具有更加明显的定位优势。

图6表示节点能量消耗与定位误差的关系。从图中发现，本文算法相比于DV-Hop、文献［2］算法的网络能量消耗都伴随着节点数量的不断增多而降低，DV-Hop算法的能量消耗曲线振幅最大，说明能量消耗不稳定，并且消耗最快，文献［2］算法次之，本文算法的能量消耗曲线平缓。说明本文算法在一定程度上可以有效提高网络能量利用率。

4　结束语

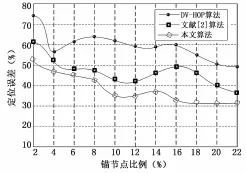
图5　锚节点的比例对定位误差的影响

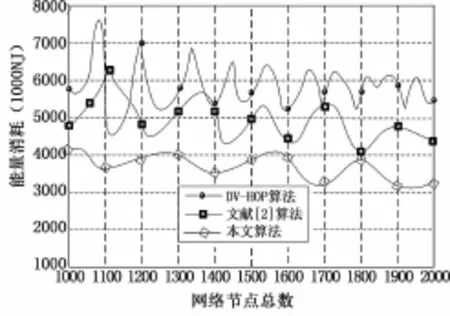
图6　节点能量能量消耗比

针对WSN中的DV-Hop算法定位的问题，本文在DVHOP算法的基础上，引入双曲线二维平面方程来定位锚节点与未知节点的关系，其次通过引入误差定位系数降低距离误差，采用Steffensen迭代法对DV-Hop算法定位结果进行分析和修正，实现精确定位。通过在仿真实验中3种算法的比较，本文的算法能够有效的提高了定位精度，具有一定的实用性。

［1］黄毅，胡爱群.无线传感器网络定位算法综述［J］.电信科学，2010，20（7）：69-74.

［2］曹欲晓，张倩，李艳冰.基于蝙蝠算法的DV-Hop定位改进［J］.计算机测量与控制，2015，23（4）：1273-1275.

［3］张万礼，宋启祥.遗传算法的DV-Hop算法改进［J］.重庆大学学报，2015，38（3）：159-166.

［4］李琳，赵可，林志贵.基于加权的三维DV-Hop定位算法［J］.控制工程，2015，22（4）：761-764.

［5］邬春明，张金强，焦龙龙.基于RSSI跳数连续的DV-HOP改进算法［J］.重庆邮电大学学报（自然科学版），2015，27（2）：184-187.

［6］蔡丽萍，蒋晶晶，洪利.一种改进的DV-HOP定位算法［J］.微电子学与计算机，2015，32（4）：120-124.

［7］柳飞，酆广增.基于RSSI和反馈机制的无线传感器网络定位优化算法［J］.南京邮电大学学报（自然科学版），2015，35（2）：108-113.

［8］苏兵，薛伟杰，王洪元.一种WSN非测距定位DV-Hop算法的误差改进方法［J］，计算机测量与控制，2013，215）：1357-1359.

［9］周杭霞，崔晨，叶佳骏.一种基于加权处理和误差修的DV-Hop定位算法研究［J］.感技术学报，2014，27（12）：1699-1703.

［10］郑远，蔡宇，赵锐.一种兼顾性能与能耗的DV-Hop改进算法 ［J］.计算机应用与软件，2014，31（4）：269-272.

Research on Positioning of an Improved DV-HOP Algorithm in Wireless Sensor Networks

Chen Lingjun
（Shaoxing Vocational&Technical College，Shaoxing312000，China）

In information transfer in WSN，signals are transferred mainly through the sensor.Aiming at the low accuracy of DV-Hop algorithm in node positioning in wireless sensor，this paper first proposes establishing hyperbolic two-dimensional model to determine the distance between anchor nodes and unknown nodes.Then，set the error coefficient to reduce errors between nodes of the sensor.Finally，Steffensen positioning method is used to modify the positioning of sensor's nodes.Simulation experiment shows that algorithm in this paper improves the positioning accuracy in remote control，and energy consumption between sensors is reduced，so it has certain promotion value.

wireless sensor network；hyperbolic two-dimensional model；error coefficient；Steffensen

1671-4598（2016）05-0305-04

10.16526/j.cnki.11-4762/tp.2016.05.084

TP212.9

A

2015-11-30；

2015-01-04。

国防预先研究项目（51327030104）。

陈玲君（1983-），女，讲师，硕士，主要从事智能控制方向的研究。