测量条干均匀度的平行板式电容传感器优化设计
2016-11-23黄胜村姚恩涛
黄胜村,姚恩涛,左 莹
(南京航空航天大学自动化学院,南京 210016)
测量条干均匀度的平行板式电容传感器优化设计
黄胜村,姚恩涛,左莹
(南京航空航天大学自动化学院,南京210016)
条干均匀度一般是指纱线沿轴向粗细变化的均匀程度;检测纱线的微小变化对仪器灵敏度等指标提出了很高的要求,因此对电容传感器的结构尺寸进行优化设计是很有必要的;文章对平行板电容传感器检测纱线的原理进行了研究,并利用电磁场有限元分析软件ANSYS,构建了平行板式电容传感器三维模型,分析了传感器极板尺寸参数的变化对灵敏度和线性度两个优化指标的影响,提出多组传感器分段检测法,完成对电容传感器尺寸的优化;另外,针对平行板电容边缘发散电场对检测结果产生干扰的问题,提出等电位保护环法,并仿真验证其对电容传感器边缘效应的抑制作用;研究结果为平行板式电容传感器优化设计提供了依据。
有限元仿真;优化设计;等电位保护环
0 引言
条干均匀度是指纱线、条子或者粗纱沿轴向较短片段内粗细或重量的均匀程度,一般用不匀率CV表示,而CV值则由纱线片段重量的标准差相对于其重量平均值的百分率计算得到。目前常用的测量条干均匀度的方法有切段称重法、黑板条干目测法和电容式传感器测量法。但是切段称重法需要将纱条按规定切成很多段进行分别称重,耗费时间较多,且对同一支纱无法实现重复测量,属于有损检测;黑板条干目测法需要人员直观的检测,对黑板规格、检验时的光照、观察距离以及检测人员本身都有一定的要求。而电容传感器具有分辨率高、响应速度快、体积小、结构简单等优点,被广泛应用。文章针对前两种检测条干均匀度的不足,提出了平行板式电容传感器检测法。纱线在两平行极板间沿着纱线轴向方向移动的过程中,由于纱线粗细变化会导致电容极板间检测区域内等效介电常数变化,从而引起电容值变化实现由非电量到电量的转化。通过后续电路处理对所测的电容信息进行分析,便可得到敏感区内被测纤维量的信息,进而计算出纤维的均匀度。
因为纤维一般都很细,其变化量更是微小,这就对电容传感器的灵敏度提出了很高的要求,所以对电容传感器的结构参数进行优化设计是很有必要的。当极板间介质不均匀时,利用解析法获得电场及电容信息是相当复杂的,因此文章利用有限元分析软件ANSYS,对平行板电容传感器进行三维仿真,通过比较传感器各结构参数对其性能的影响,优化结构参数,最后通过仿真验证了施加等电位保护环对于抑制电容传感器边缘效应的作用,从而保证了测量结果的准确性。
1 平行板电容传感器检测原理
假设为极板间空气的相对介电常数,为纱线的相对介电常数,Sa为极板正对面积,纱线层与极板平行,D为极板间距,d为纱线层模型的厚度,理想情况下认为极板足够薄,厚度不计,极板足够长,忽略其边缘效应。平行板电容传感器的理想物理模型如图1所示。
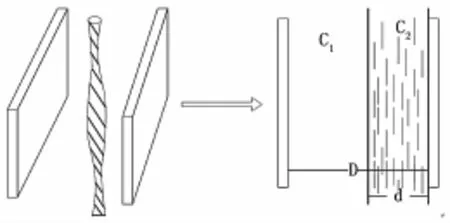
图1 变介质式平行极板电容传感器
根据平行板电容的计算公式,有:
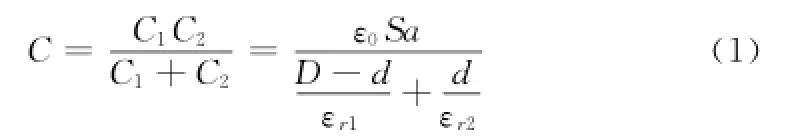
若空气的相对介电常数为1,则有:
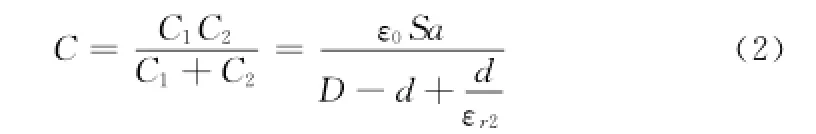
如果极板间纤维的厚度发生变化,电容器的等效电容C将随之改变,式(2)是平行板式电容传感器测量的理论基础。通过后续电路处理对所测的电容信息进行分析,便可得到敏感区内被测纤维量的统计信息,进而计算出纤维的均匀度。
2 电容传感器优化指标
由于纱线一般都非常细,其沿轴向的均匀程度更难被感知,这就对传感器的灵敏度提出了很高的要求;另外,利用电容传感器测量条干均匀度是通过获得电容信息反向求解纤维重量(体积)信息,较好的线性度有利于纤维重量信息的统计。
考虑到灵敏度及线性度对统计得到的纤维重量的标准方差S和平均值X的影响,文中将传感器的灵敏度和线性度作为主要性能指标对极板结构参数进行优化设计,来提高测量条干均匀度的准确性。
1)灵敏度,作为传感器优化的重要指标,其定义为:纱线接入敏感区后,由纱线重量(体积)变化引起的电容的相对变化量与纱线重量变化量的比值。
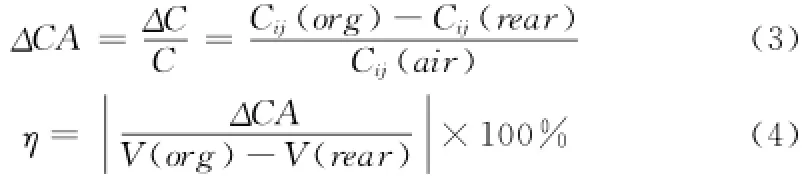
式中,η为传感器的灵敏度,ΔCA为纱线变化引起的电容相对变化量,Cij(org)为敏感区放入固定型号纱线的电容值,Cij(rear)为纱线量变化后传感器的电容值,Cij(air)为空载(介质只有空气)时的静态电容值;V(org)为接入敏感区内的纱线的体积,V(rear)为敏感区内纱线量变化后的体积。在电容的相对变化量与纱线重量(体积)关系曲线中,其斜率的大小即为传感器的灵敏度大小,并且斜率越大,表示传感器的灵敏度越高。
2)线性度,描述传感器静态特性的重要指标,其定义为:表征传感器输出-输入校准曲线与所选定的作为工作直线的拟合直线之间的偏离程度,该指标以相对误差表示。ES
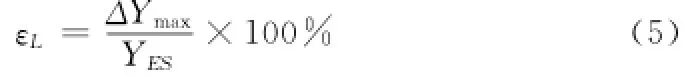
式中,ΔYmax为输出曲线与拟合直线间的最大偏差;YES为满量程输出。由公式(5)可知,εL值越小,传感器的线性度越高。
3 有限元分析
3.1电容传感器的有限元法计算
根据有限元的思想,静电场问题的有限元分析法就是求静电场能量泛函的极值问题。静电场中各点的电位可用泊松方程来描述,三维静电场的泊松方程为:
▽·[ε(x,y,z)▽φ(x,y,z)]=-ρ(x,y,z)(6)式中,ε(x,y,z)为空间的介电常数;φ(x,y,z)为电场中各点的电位;ρ(x,y,z)为空间电荷密度,通常认为电容传感器的检测场内无自由电荷,即ρ(x,y,z)=0。此时,式(6)变为式(7)电磁场中的拉普拉斯方程。
▽·[ε(x,y,z)▽φ(x,y,z)]=0(7)
即电容传感器的敏感场可由拉普拉斯方程描述为:
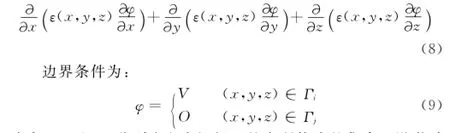
式中,Γi和Γj分别为电容极板上的点所构成的集合。设激励极板i施加电压V,检测极板j接地。利用高斯定理可计算出极板j上的感应电荷:
Qi=φ((x,y,z)∈Γj)ε(x,y,z)▽Ø(x,y,z)dΓj(10)
电极i和电极j之间的电容可通过如下公式(6)求得:

3.2ANSYS建模与网格剖分
为了便于建立物理模型进行仿真分析,文中将纱线实体抽象为几何中的圆柱体模型,并且将纺织行业中衡量纱线粗细的计量单位特克斯近似转化为几何中圆柱体的直径大小。
利用ANSYS有限元软件进行分析的基本过程主要包括创建有限元模型、施加载荷进行求解以及查看分析结果三部分。仿真模型如图2所示(规定沿纱线方向的极板长度W定义为极板纵向长度,垂直纱线方向的极板长度L定义为极板横向长度,极板间距为D)。

图2 ansys环境下纤维与极板仿真模型
设定好各个极板参数并建立好有限元模型后,利用网格剖分工具对传感器敏感区及空气区域进行剖分,然后使用软件自带的CMATRIX命令即可计算出极板间的电容值。其直接作用就是通过求取传感器敏感区内电位分布,然后通过后处理程序计算电容值。最后通过对数据的处理,进一步分析平行板电容极板参数对检测纱线灵敏度及线性度的影响。
3.3参数设置
依据常用纱线的测量范围,针对影响测量结果的因素——极板横向长度和极板间距。选取不同的极板横向长度和极板间距,设计一组不同尺寸组合的传感器,将直径依次递增的纱线放入平行板电容器中心的位置,进行建模仿真,然后分析不同极板参数对于电容传感器检测纱线性能的影响。图3是在极板横向长度L由L 1到L6依次增大,其他参数保持不变时测得的纤维体积与极板电容相对变化量的关系曲线;图4是在极板间距D由D 1到D7依次增大,其他参数保持不变时测得的纤维体积与极板电容相对变化量的关系曲线。
3.4性能指标比较
通过ANSYS仿真计算得到传感器在不同电极结构下的电容值,分析比较各结构参数对灵敏度及线性度的影响。
1)极板横向长度的影响:由图3可以看出,当极板间距取定时,极板横向长度越小,检测纱线的灵敏度越高,但是在整个测量区间内线性度会变差。
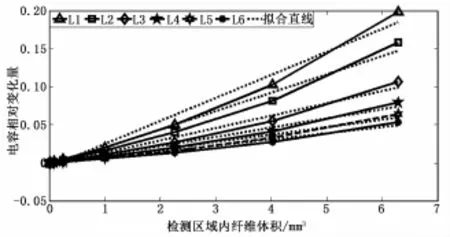
图3 不同极板横向长度下,纤维体积与极板电容相对变化量的关系曲线及拟合直线图
2)极板间距的影响:由图4可以看出,当极板横向长度取定后,极板间距越小,检测纱线的灵敏度越高,同样会使得其线性度变差。

图4 不同极板间距下,纤维体积与极板电容相对变化量的关系曲线及拟合直线图
3)纤维量的影响:由图3和图4都可以看出,当传感器结构参数固定时,随着检测区域内纱线体积变大(即纱线变粗),检测纱线的灵敏度变大,但是会使得整个测量范围内的线性度变差。
4)极板横向长度与极板间距的影响对比:极板间距对检测灵敏度的影响较极板横向长度对检测灵敏度的影响大得多,或者说极板间距对于调节检测纱线灵敏度起主要作用,极板横向长度主要用来改变信号强度,调整电容传感器的电容值。
3.5传感器尺寸设计
由3.4中的分析可以看出,电容传感器在检测纤维的整个范围内无法同时兼顾灵敏度和线性度两个指标。文中将灵敏度作为优先考虑的指标,在满足较高灵敏度的前提下,力求能有较理想的线性度。
由上述分析可知,极板间距对电容传感器的灵敏度有更为显著的影响,且间距越小灵敏度越高。因此,参考3.4中的分析结果以及进一步的仿真实验,设定了4个间距不同的电容传感器。为了满足线性度的要求,根据极板间距的不同将纤维的检测范围划分为4个区间,从而最大限度地保证4个传感器在各自的检测区间内都有较高的灵敏度及较理想的线性度。
另外,通过设定合适的极板横向长度,保证电容传感器有合适的电容值,便于后续电路检测电容信息。
图5~8为所设计的4个电容传感器在各自检测范围内,纤维体积与极板电容相对变化量的关系曲线及拟合直线图。可以看出,所设计的电容传感器组合整个检测范围内都能有较高的灵敏度和较好的线性度。
4 边缘效应抑制
通过以上仿真,使平行板电容传感器的结构得到优化,满足了检测纤维的灵敏度和线性度的要求。但是两平行金属极板的边缘存在发散电场,该发散电场形成边缘附加电容,影响到后续电路对传感器电容信息的检测,进而影响纤维均匀度的计算结果。
在不加等电位保护环进行屏蔽时,传感器的截面电位分布如图9所示 (该图是沿着纤维方向看进去的俯视图),图中左右两侧为传感器极板,中间部位为检测区域。由图9可以看出,无屏蔽极板的电容传感器中检测区域的电位分布很不均匀。
按照图10所示的方式接入等电位保护环,并且保证每一侧保护环电位与同侧的传感器极板等电位。
接入等电位保护环后的传感器截面电位分布图如图11所示,可以看出检测区域内的电位分布比较均匀。
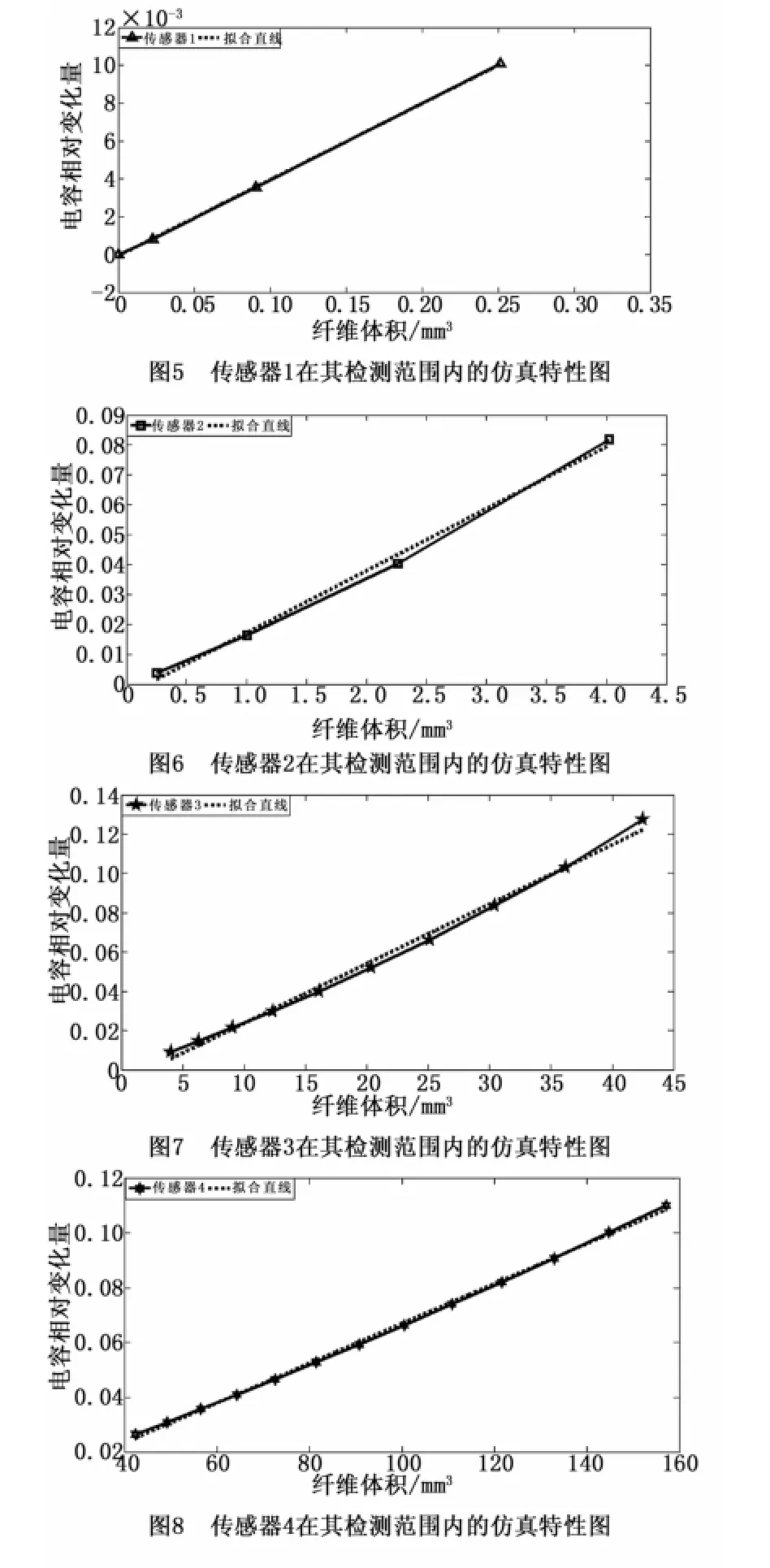

图9 未加等电位保护环,传感器电位分布图
由于电力线垂直于图中的等位线,可以看出未接入等电位保护环时电容传感器的电力线有向外发散的趋势,特别是靠近两侧极板附近以及敏感区的边缘处,导致传感器敏感场内不同位置的灵敏度不同,检测结果会出现很大偏差。而带有等电位保护环的电容传感器在检测区域内电力线发散性较小,传感器的边缘效应得到有效抑制,灵敏度分布比较均匀,在不同位置进行测量时,测量结果偏差不会太大。另外,为了最大限度的减小测量偏差,应该尽量将纱线置于检测区域中间部位。
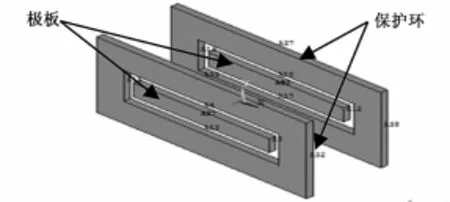
图10 等电位保护环模型

图11 接入等电位保护环,传感器电位分布图
5 结论
文章使用ANSYS有限元分析软件,构建了平行极板电容传感器与待测纤维量的三维模型,对传感器各结构参数进行优化设计,仿真结果表明,经优化后的传感器可以满足检测纤维的灵敏度及线性度的要求,保证了检测条干均匀度的准确性。通过对极板接入等电位保护环,有效抑制了电容传感器的边缘效应,使传感器的灵敏场更加均匀,为传感器的优化设计提供了依据,同时也为计算纱线的条干不匀度奠定了基础。
本文提出了一种新型多功能信号源设计方案,详细阐述了信号源系统的硬件及软件设计,方案设计兼顾标准化、高速、可靠性3个方面,可实现多类型、多通道信号的发送,系统工作稳定、可靠性高,实验结果表明,该方案满足设计需求,该套系统已成功应用于飞行试验中,系统采用模块化与通用化的设计思路,对其他领域的应用也有一定的参考价值。
[1]张君,许锦峰,姚恩涛,等.测量围护结构含水率的同面散射场式电容传感器设计[J].计测技术,2008,28(1):7-11.
[2]曹河,董恩生,范作宪,等.同面多电极电容传感器优化设计[J].计算机测量与控制,2013.21(6):1711-1714.
[3]曲开文.电容传感器的三维静电场分析及其优化设计[D].沈阳:东北大学,2010.
[4]王兆华.基于有源电桥的电容式传感器及其测量系统的研究[D].北京:北京化工大学,2006.
[5]李宁波.纱条条干均匀度测试仪新型专用电容传感器的研究[D].西安:西安工程科技学院,2005.
[6]樊玉铭,赵鸿林.条干不均匀度检测装置中电容传感器的研究[J].天津大学学报,1996,29(6):930-937.
Optimal Design of Parallel-plate Capacitance Sensors for Measuring Yarn Evenness
Huang Shengcun,Yao Entao,Zuo Ying
(College of Automation Engineering,Nanjing University of Aeronautics& Astronautics,Nanjing210016,China)
Evenness refers to the uniformity of yarn in the axial direction.It is necessary to optimize the size of capacitive sensors,so as to detect little changes of yarn.The article studies the principle of detecting the quantity of yarn with parallel plate capacitance sensor,then constructs three-dimensional model using finite element analysis software to analyze the influence of size on sensitivity and linearity of sensors.Finally the optimal size is obtained with the method of muti-segmented detection.In addition,equipotential protection ring is proposed to restrain the interference caused by diverging electric field,and the method has been verified by ANSYS.The research results provide the basis for the optimal design of the parallel plate capacitance sensor.
finite element simulation;optimal design;equipotential protection ring
1671-4598(2016)05-0298-04
10.16526/j.cnki.11-4762/tp.2016.05.082
TB971
A
2015-10-21;
2015-12-04。
黄胜村(1991-),男,河北邢台人,硕士研究生,主要从事智能传感技术及系统方向的研究。
