基于改进熵权-TOPSIS的隧道塌方风险等级分类

陈 诚

(黄河水利职业技术学院，河南开封475003)



基于改进熵权-TOPSIS的隧道塌方风险等级分类

陈 诚

(黄河水利职业技术学院，河南开封475003)

针对理想点法的基本原理，建立了基于理想点法的隧道塌方风险等级评价模型，并应用到隧道施工塌方风险评价中，该方法考虑了塌方中的不确定因素和指标之间的关联性等问题，从理想状态出发，寻求隧道塌方风险等级的所属类别，评价结果更为可靠。

隧道；塌方；风险评价；理想点法；熵权法

0 引 言

隧道的防塌、防治安全评估工作具有重要意义[1]。隧道塌方风险评价研究成果众多，杨光等[2]将云模型理论引入到隧道塌方风险评价中，借助云模型理论可以实现定性、定量转换的优势，采用最大综合确定度给出隧道塌方风险等级；周宗青等[3]运用地质调查方法建立了隧道塌方的风险模糊层次评价模型，同时结合施工过程中获取的动态信息，实现了风险的动态评估；苏永华等[4]针对传统方法中指标赋权方法的不足，引入粗糙集重心理论进行改进，选取6大塌方风险因素并结合工程实例进行验证；何美丽等[5]基于未确知测度模型，建立了隧道塌方与其影响因子之间的未确知系统，采用6个实测因子作为风险评价体系，并将评价结果与工程实际情况进行对比；曹文贵等[6]将集对分析方法引入到隧道塌方风险评价中，筛选了影响塌方的主要影响因素，针对评价指标中确定与不确定信息并存的特点，根据集对分析理论给出评价结果。此外，经过众多学者的不懈努力得到了大量的研究成果，如模糊层次分析[7]、属性识别模型[8]、多级模糊综合评判[9]、事故树分析[10]、突变理论[11]、时空预测模型[12]等。上述方法对隧道塌方风险评价的研究进展起到了重要的推动作用。但是，由于理论自身的缺陷或受制于客观条件，皆不能很好地用于工程实际中，难以准确反映隧道塌方的孕育机理。因此，有必要寻找新的隧道塌方风险评价方法。

理想点法(TOPSIS)是一种常用的多目标决策分析法，其基本思路是通过构造多指标问题的理想解和反理想解，并以靠近理想解和远离反理想解的程度作为各评价对象的判断依据。文献[13- 16]分别建立了基于理想点法的隧道围岩分类模型和基于理想点法的岩爆烈度分级预测模型，给出围岩分类结果和岩爆烈度预测等级，但在岩土工程中应用较少。本文将理想点法应用到洞室常见的围岩分类中，并且在确定各评价指标权重时，采用了更客观更科学的方法——改进的熵权法，把权重问题转变为由现场实测数据求解各指标属性重要性问题，建立了基于改进熵权的理想点法，并应用于实际工程的隧道塌方风险评价中。

1 基本理论

1.1 理想点法

理想点法的应用过程为：①在确定评价指标体系和各指标权重的基础上定义一种模，即n维欧氏空间中的1个点。②找到1个尽量接近理想点的点，使反理想点的评价函数值最大和理想点的评价函数值最小，并构造出相应的贴近度函数。③通过理想点贴近度来判断各评价对象所属的类别。

1.1.1 隧道塌方风险评价指标体系的构建

(1)

1.1.2 理想点和反理想点

在常规评价指标中，评价指标一般可归纳为正指标和逆指标。正指标量值越大意味着评价结果越危险，逆指标量值越小意味着评价结果危险。根据正指标和逆指标的意义，可以定义理想点和反理想点，即

(2)

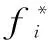
1.1.3 理想点函数构建

评价指标与理想点间的距离即为理想点函数。评价指标与正理想点之间的距离越小，与反理想点之间的距离越大，则表明评价指标越优，基于此，在n维空间可以定义模

‖f(x)-f*(+)‖→min,‖f(x)-f*(-)‖→max

(3)

理想点函数一般采用欧式距离和闵可夫斯基(Minkowski)距离。当采用闵可夫斯基距离时，评价指标与正理想点之间的距离D1为

(4)

式中，P根据实际情况确定。当P=1时，评价指标与理想点(负理想点)间的距离就是绝对距离或海明距离；当P=2时，就是欧式距离；当P=时，就是切比雪夫距离。

评价指标与负理想点之间的距离为

(5)

1.1.4 理想点贴近度

根据理想点函数确定评价指标与理想点距离后，理想点贴近度T的计算公式为

T=D2/(D1+D2)

(6)

式中，0≤T≤1，贴近度T的量值越大，则表示与理想点的距离越小，与反理想点的距离越大；反之亦然。

1.2 熵权法

熵权法通过建立评价指标的矩阵来计算各指标的熵值，熵值越大表明该指标提供的有效信息越少，熵值越小表明提供的有效信息越多。因此，熵权法可以根据评价指标的熵值大小对其进行赋权，熵值越大，权重越小；反之亦然。熵权法得出的结果客观公正，人为干涉少，能较为准确的反映各指标的实际情况。本文采用熵权法计算隧道塌方风险评价指标的权重。

对于隧道塌方风险评价的n个评价指标的m个测值，构建评价指标矩阵X=[xij]n×m，xij表示指标i的第j个测值。归一化后的评价指标矩阵为Y=[yij]m×n。根据信息熵的定义，指标i的熵值ei可以表示为

(7)

式中，k为参数。

定义偏差度di为

di=1-ei

(8)

根据熵权法可知，评价指标的权重wi可由下式给出

(9)

采用式(9)求解指标权重时，若熵值ei→1，则得出的权重结果会不准确，如当熵值取(0.999，0.998，0.997)时，权重结果为(0.117，0.333，0.5)，可以发现熵值仅变化1‰，而权重结果却变化了65%和33%，明显不合理。为此，对式(9)作如下调整

(10)

式中，et为指标t的熵值；el为指标l的熵值。

1.3 基于熵权-理想点法耦合的综合评估模型

在隧道塌方风险评价指标的权重计算时，应收集历史观测数据，获得隧道的完整资料，尽可能真实地反映隧道的工作性态。指标权重确定后，根据本文建立的综合评价模型得到理想点贴近度值，从而给出隧道塌方风险评价结果。隧道塌方评价流程见图1。

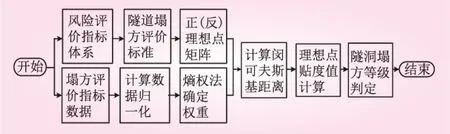
图1 隧道塌方评价流程

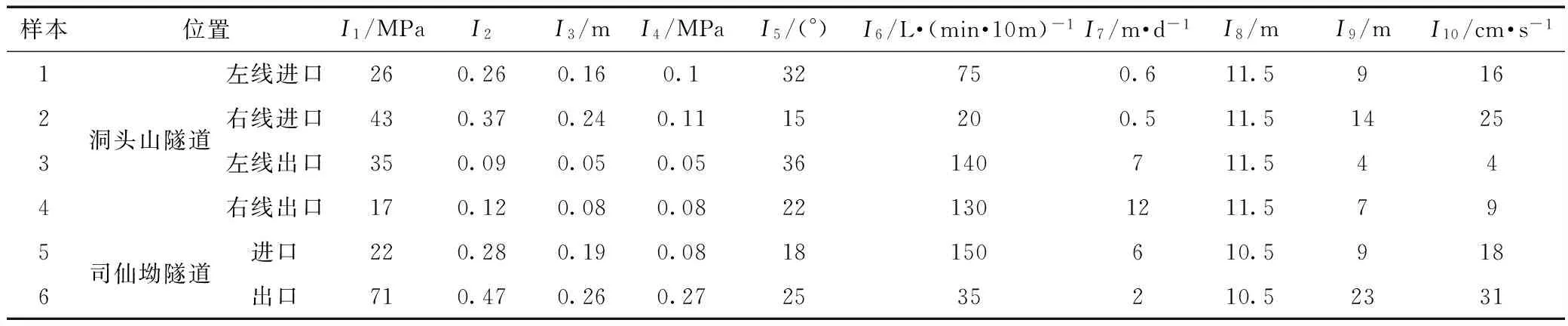
样本位置I1/MPaI2I3/mI4/MPaI5/(°)I6/L·(min·10m)-1I7/m·d-1I8/mI9/mI10/cm·s-11234洞头山隧道左线进口260.260.160.132750.611.5916右线进口430.370.240.1115200.511.51425左线出口350.090.050.0536140711.544右线出口170.120.080.08221301211.57956司仙坳隧道进口220.280.190.0818150610.5918出口710.470.260.272535210.52331

2 工程实例

选取2个开挖隧洞实例建模验证。影响隧道塌方的因素很多，包括隧道的断面尺寸、开挖方式、土质、降雨、结构面、软弱夹层、人为扰动等。本文根据所选样本的实际特点，结合已有的研究成果，选取岩石单轴饱和抗压强度Rc、岩体完整性指数Kv、节理面平均间距Jd、结构面粘聚力c、偏压角度θ、地下水渗水量K1、含水层透水性K2、隧道跨度D、隧道埋深H及施工对围岩的扰动量作为本次隧道塌方风险评价的指标体系。 其中，施工对围岩的扰动量采用质点峰值速度PPV表示。隧道塌方风险评价指标体系见图2。

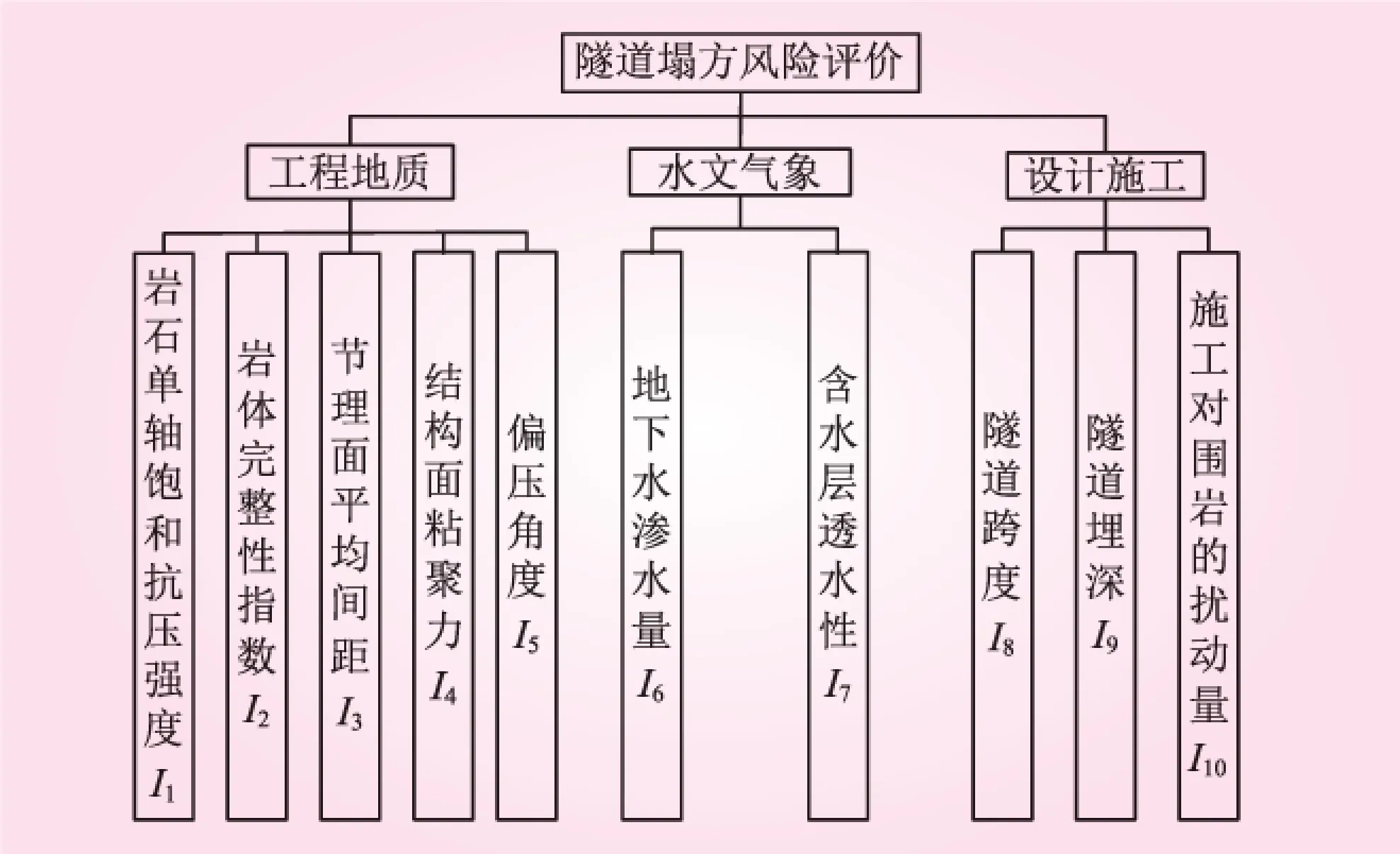
图2 隧道塌方风险评价指标体系

本文选取的代表性隧道的塌方风险评价指标的实测资料见表1。由表1可知，各隧道之间的差异性较大。

在图2拟定的10个隧道塌方风险评价指标的基础上，结合工程概况以及已有的研究成果，对隧道塌方风险等级进行划分，各评价指标标准见表2。

表2 各评价指标标准

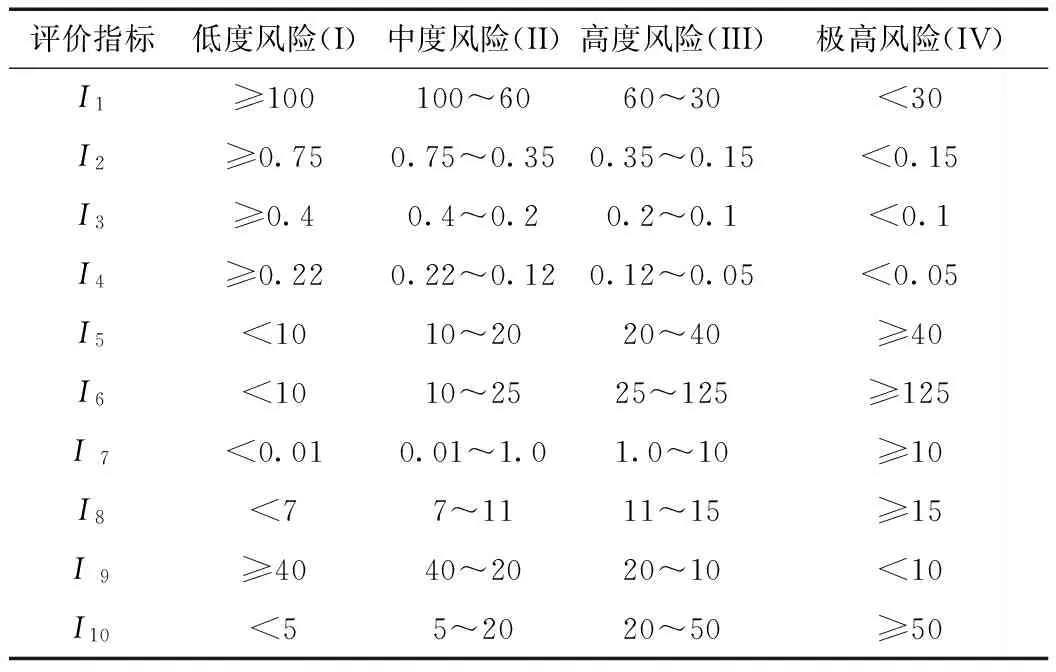
评价指标低度风险(I)中度风险(II)高度风险(III)极高风险(IV)I1≥100100～6060～30<30I2≥0.750.75～0.350.35～0.15<0.15I3≥0.40.4～0.20.2～0.1<0.1I4≥0.220.22～0.120.12～0.05<0.05I5<1010～2020～40≥40I6<1010～2525～125≥125I7<0.010.01～1.01.0～10≥10I8<77～1111～15≥15I9≥4040～2020～10<10I10<55～2020～50≥50

3 风险评价

3.1 理想点和反理想点的计算

本文建立的隧道塌方风险评价分级标准中，地下水渗水量、含水层透水性、隧道跨度、施工对围岩的扰动量为正指标，量值越大，隧道塌方风险越高。岩石单轴饱和抗压强度、岩体完整性指数、节理面平均间距、结构面粘聚力、偏压角度、隧道埋深为逆指标，量值越大，隧道塌方风险越低。将表2中隧道塌方风险评价指标标准的上、下分界值选取为正理想点和反理想点，计算隧道塌方风险评价指标的理想点矩阵F*(+)和F*(-)

F*(+)=

(11)

F*(-)=

(12)

3.2 评价指标权重的确定

根据本文提出的改进熵权法，对本次拟定的隧道塌方风险评价指标体系进行赋权。各指标权重见表3。

表3 各指标权重

评价指标I1I2I3I4I5I6I7I8I9I10投影寻踪0.1690.1310.0480.0520.0510.1190.0730.0880.0580.141权重Wj0.1750.1250.050.050.10.120.080.090.060.15

3.3 隧道塌方风险级别判定

各评价指标的理想点距离值及相应的权重系数确定后，即可得到待评价对象的理想点贴近度。因此，根据本文所建模型，在既定的隧道塌方风险评价指标体系及相应标准的基础上，由隧道实测数据计算待评价对象的理想点贴近度，最后根据最大隶属度原则给出最终评价结果。各隧道评价结果见表4。

表4 各隧道评价结果

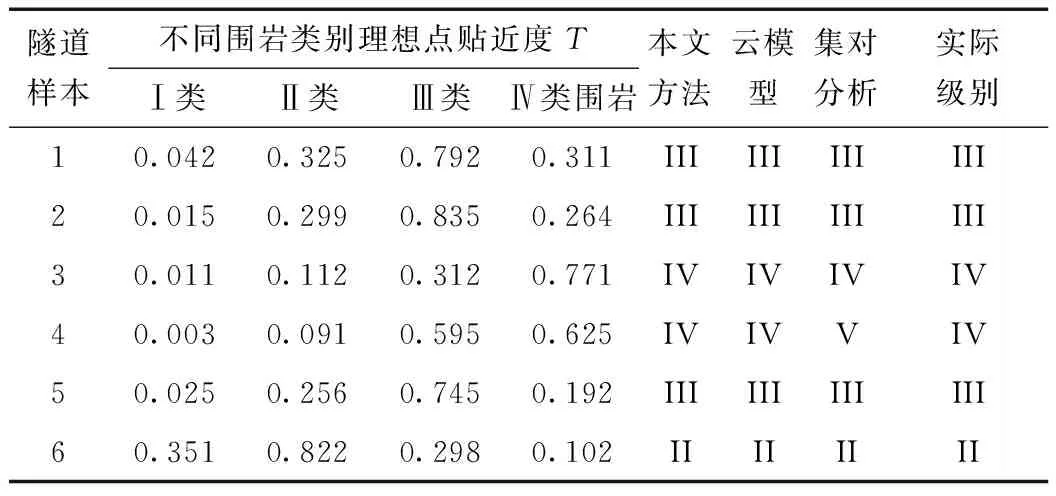
隧道样本不同围岩类别理想点贴近度TⅠ类Ⅱ类Ⅲ类Ⅳ类围岩本文方法云模型集对分析实际级别10.0420.3250.7920.311IIIIIIIIIIII20.0150.2990.8350.264IIIIIIIIIIII30.0110.1120.3120.771IVIVIVIV40.0030.0910.5950.625IVIVVIV50.0250.2560.7450.192IIIIIIIIIIII60.3510.8220.2980.102IIIIIIII

从表4可以看出，理想点法给出的评价结果与云模型和集对分析方法给出的评价结果基本一致，这也证明了本文方法的可行性和准确性。仅样本4中，本文给出的结果为IV级，集对分析为V级，实际级别为IV级，存在一定偏差，但3种方法给出的结果基本相近。在现场巡视中，样本4的岩石较差，有断层、软弱夹层的存在。在样本4上选择5个具有代表性的点用小锤轻击时，出现了明显的颗粒散落。因此，通过理想点法给出的评价结果与实际情况也是相符的，这也证明了本文方法的可行性。

4 结 语

将理想点法引入到隧道塌方风险评价中，根据工程特征和前人研究成果建立了地质环境条件与气象因素相耦合的综合评价指标体系，为隧道塌方风险评价提供了一种新的思路和方法。

以岩石单轴饱和抗压强度等9个指标作为评价因子，建立了隧道塌方风险评价的功效系数分析模型。利用2个典型工程实例进行验证，并与云模型和集对分析法的判别结果进行对比表明，运用该模型对隧道塌方进行风险评价是合理、可行的。

[1]陈龙， 黄宏伟. 岩石隧道工程风险浅析[J]. 岩石力学与工程学报， 2005， 24(1)： 110- 115．

[2]杨光， 刘敦文， 褚夫蛟， 等. 基于云模型的隧道塌方风险等级评价[J]. 中国安全生产科学技术， 2015， 11(6)： 95- 101．

[3]周宗青， 李术才， 李利平， 等. 浅埋隧道塌方地质灾害成因及风险控制[J]. 岩土力学， 2013， 34(5)： 1375- 1382．

[4]苏永华， 刘科伟， 张进华. 基于粗糙集重心理论的公路隧道塌方风险分析[J]. 湖南大学学报： 自然科学版， 2013， 40(1)： 21- 26．

[5]何美丽， 刘霁， 刘浪， 等. 隧道塌方风险评价的未确知测度模型及工程应用[J]. 中南大学学报： 自然科学版， 2012， 43(9)： 3665- 3671．

[6]曹文贵， 翟友成， 王江营， 等. 山岭隧道塌方风险的集对分析方法[J]. 中国公路学报， 2012， 25(2)： 90- 99．

[7]徐善初， 张世林， 陈建平. 模糊层次评价法在隧道地质灾害评估中的应用[J]. 地下空间与工程学报， 2013， 9(4)： 946- 953．

[8]李术才， 石少帅， 李利平， 等. 山岭隧道塌方风险评价的属性识别模型与应用[J]. 应用基础与工程科学学报， 2013， 21(1)： 147- 158．

[9]刘学增， 包浩杉， 米东阳. 公路隧道穿越断层塌方预测多级模糊综合评判[J]. 现代隧道技术， 2011， 48(6)： 65- 71．

[10]周建昆， 吴坚. 岩石公路隧道塌方风险事故树分析[J]. 地下空间与工程学报， 2008， 4(6)： 991- 998.

[11]胡长明， 贡少瑞， 张超晖， 等. 基于突变理论的山岭隧道塌方风险预测[J]. 西安建筑科技大学学报： 自然科学版， 2014， 46(1)： 10- 15．[12]王迎超， 尚岳全， 徐兴华， 等. 隧道出洞口松散围岩塌方时空预测研究[J]. 岩土工程学报， 2010， 32(12)： 1868- 1874．

[13]王迎超， 尚岳全， 孙红月， 等. 基于熵权-理想点法的岩爆烈度预测模型及其应用[J]. 煤炭学报， 2010， 35(2)： 218- 221．

[14]王迎超， 孙红月， 尚岳全， 等. 基于特尔菲-理想点法的隧道围岩分类研究[J]. 岩土工程学报， 2011， 32(4)： 651- 656．

[15]张乐文， 邱道宏， 李术才， 等. 基于粗糙集和理想点法的隧道围岩分类研究[J]. 岩土力学， 2011， 35(S1)： 171- 175．

[16]贾义鹏， 吕庆， 尚岳全， 等. 基于粗糙集-理想点法的岩爆预测[J]. 浙江大学学报： 工学版， 2014， 37(3)： 498- 503．

(责任编辑 杨 健)

Risk Grade Evaluation of Tunnel Collapse Based on Entropy Weight Method-TOPSIS

CHEN Cheng

(Yellow River Conservancy Technical Institute, Kaifeng 475003, Henan, China)

Based on the basic principles of Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), a model is established to evaluate the risk degree of tunnel collapse. The model has taken into account the uncertainties associated with landslides and the interrelation between indicators. The model has been applied to the collapse risk assessment of tunnel starting from the ideal state. The model can determine the risk grade of tunnel collapse and the evaluation result is more reliable．

tunnel; collapse; risk evaluation; TOPSIS; entropy weight method

2016- 01- 04

河南省高等学校青年骨干教师资助计划资助项目 (2011GGJS- 188)；河南省教育厅科学研究重点项目(14A570004)

陈诚(1972—)，男，河南开封人，副教授，硕士，研究方向为水利工程安全与经济评价．

U458.3

A

0559- 9342(2016)06- 0030- 04