基于融合权重-云模型的地下水水质评价方法研究

王瑞星

(内蒙古农业大学职业技术学院，内蒙古包头014109)



基于融合权重-云模型的地下水水质评价方法研究

王瑞星

(内蒙古农业大学职业技术学院，内蒙古包头014109)

鉴于地下水水质评价中各指标的不确定性和模糊性，将融合权重与云模型相结合，应用于地下水水质综合评价中，建立了基于融合权重-云综合模型。引用融合权重所反映数据本身的效用值来计算指标的权重系数，有效地避免了权重分配困难的问题。该模型以一种新的方法进行地下水水质综合评价，并应用于工程实例，通过与模糊物元法和投影寻踪法的比较，进一步验证了该模型的合理、简便和实用性。

地下水；水质评价；融合权重；正态云

0 引 言

地下水水质综合评价就是根据水质指标值，通过所建立的数学模型，对水体水质等级进行综合评判，为水体的科学管理和污染防治提供决策依据。由于实际水体各单项水质指标的评价结果常常是不相容的，直接利用水质评价标准表进行水体质量等级评判缺乏实用性。因此，许多学者在水质综合评价领域进行了深入研究。目前，水质评价的数学模型很多，每种模型都有自身的优点和不足，常用的有主成分分析法[1]、层次分析法[2]和模糊数学法[3]、内梅罗指数法[4]、投影寻踪模型[5]、BP神经网络[6]、灰色聚类决策模型[7]、集对法[8]、相对隶属度理论[9]和模糊概率模型[10]等。主成分分析法进行评价时，因子负荷符号交替使函数意义不明确，需要大量的统计数据，不能反映客观发展水平；层次分析法无论是建立层次结构还是构造判断矩阵，人的主观判断、选择、偏好对评价结果的影响极大，判断失误就可能造成决策失误；模糊数学方法不能解决评价指标相关造成的信息重复问题，评价精度一般较低。

上述研究成果对水质综合评价的研究进展起到了重要的推动作用。但水质综合评价指标与相应标准具有一定的随机性和模糊性，上述方法还很难适应这一问题。本文将融合权重与云模型相结合，建立了基于融合权重-云综合模型，引用融合权重所反映数据本身的效用值来计算指标的权重系数，有效地避免了权重分配困难的问题，以实现合理、高效利用地下水资源的目的。

1 基于云模型的水质分级

1.1 云模型理论

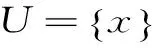
正态云主要采用期望Ex、熵En和超熵He这3个数字特征表示，这3个数字特征反映了水质评价中的定性概念与其定量表示。其中，期望Ex是水质评价中论域U的中心值，也是定性概念C的最典型样本值；熵En为水质评价中定性概念C的模糊性的度量，反映了水质评价中论域U中可被定性概念C接受的定量区间；超熵He是熵En的熵，反映了正态云模型中云滴的凝聚程度，当超熵He等于零时，正态云也就演变成了正态曲线。

根据云模型正向发生器生成所需的云滴，可构建本次水质评价的正态云模型，云模型正向发生器的实现过程如下：

(1)根据水质评价指标的实测数据，得到云模型数字特征熵En和超熵He。

(2)根据得到的云模型数字特征，采用统计学方法生成正态随机数。

(3)根据生成的正态随机数，由式μ=e-(x-Ex)2/(2En′2)计算确定度值，即可得到一个云滴。

(4) 循环上述步骤，生成足够多的云滴。

1.2 水质分级云模型的特征参数

水质综合评价中，需要预先确定相应的云模型特征值Ex、En和He，表达式如下

(1)

在水质综合评价中，由于评价标准的边界值具有一定的模糊性，可以分属相邻等级，故隶属度应当相等，即

(2)

不难得到云模型的熵，即

(3)

He一般按下式取值

He=k

(4)

式中，k为某一确定常数，可通过云模型的离散程度进行调整。

2 水质评价指标体系及权重确定

本次采用北京市朝阳区的地下水水体建模验证，朝阳区总面积470.8 km2，全区人口308.3万，区域内商业发达，淡水消耗量较大，日常用水以地下水为主。为了实时获取地下水水体的水质性态，在该区内布置有19个地下水质监测井(见图1)。

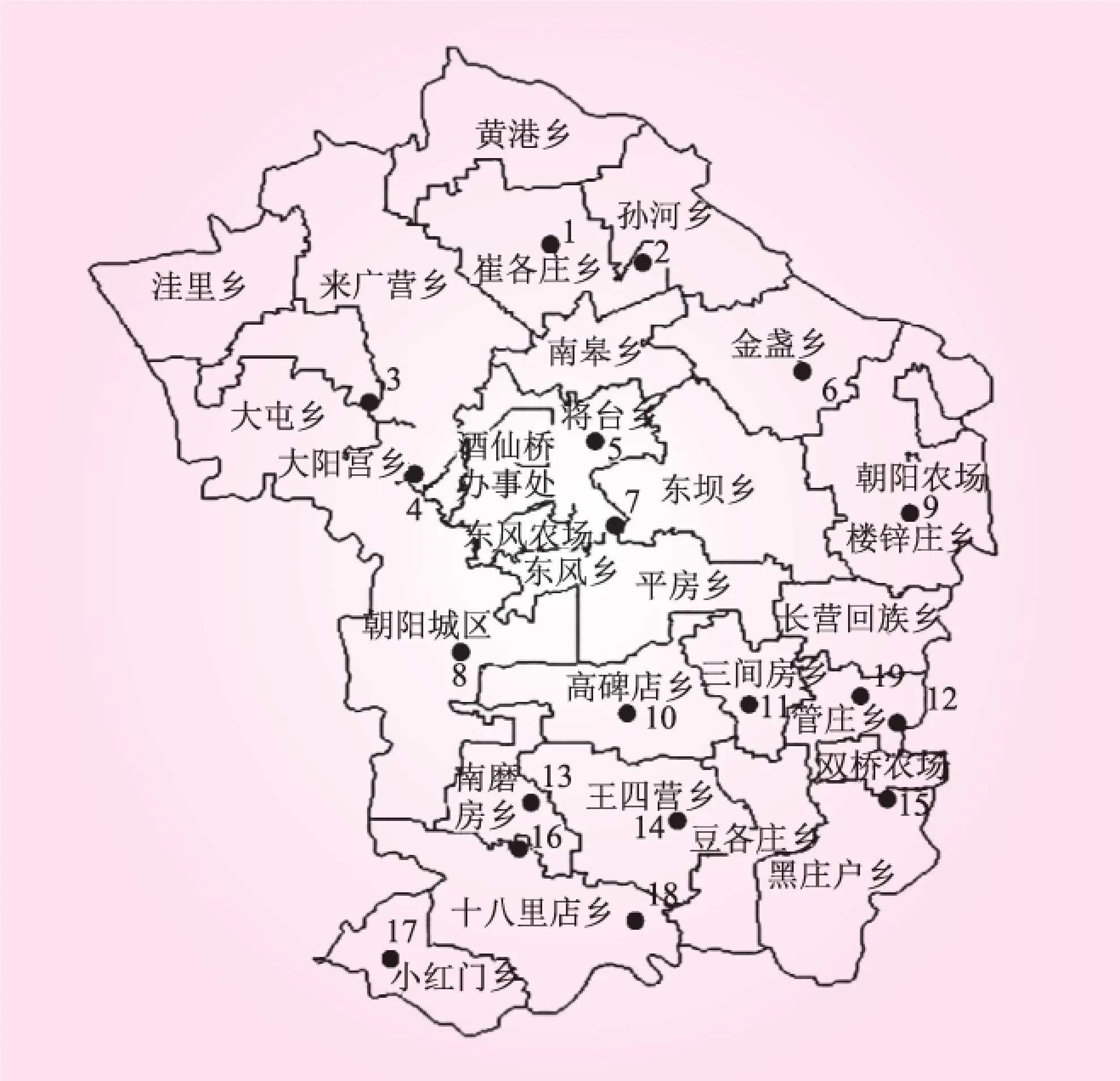
图1 水质监测井位置

2.1 水质分级的指标体系

地下水水体质量受多种因素影响，建立一个合理、有效的水质评价指标体系是水质综合评价的关键，而水体中的化学元素对水体质量影响尤甚。基于此，在文献[11]的基础上，选取了氨氮I1、亚硝酸盐I2、溶解性总固体I3、高锰酸盐指数I4、总硬度I5、硝酸盐I6、氟化物I7、氯化物I8以及硫酸盐I9等9个指标作为本次水质评价指标体系。在既定体系的基础上，根据GB/T 148—1993《中华人民共和国地下水质量标准》，拟定了相应的评价标准。水质等级与指标体系间的关系见表1。

2.2 基于融合权重的水质综合评价指标权重确定

参阅已有文献可知，水质评价指标的赋权法有投影寻踪法(Projection Pursuit Analysis，简称PPA)、Delphi法、粗糙集理论以及熵权法等。本次选取1组主、客观赋权法，在此基础上，以融合权重结果作为综合权重。

表1 水质等级与指标体系间的关系 mg/L

2.2.1 基于投影寻踪法的权重确定

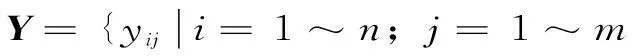
(5)

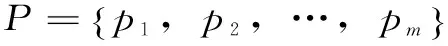
在yij已知的情况下，只需要确定投影方向P就可以得到评价指标i的投影值G(i)。通过调整P的方向，使得H(p)的值最大来确定P的最佳投影方向，方程如下

Max:H(p)=SG·QG

(6)

限于篇幅，式(6)的求解过程可参考文献[5]。得到最佳投影方向P*后，代入式(5)计算最佳投影值G(i)*，则各水质评价指标的权重wi为

(7)

2.2.2 基于改进层次分析法的权重确定

设有n阶实数矩阵A、B、C，并满足以下定义：

(1)若aij=1/aij，且aij=aik/ajk，则称A为互反矩阵，且是一致的。

(2)若bij=-bij，且bij=bik-bjk，则称B为反对称矩阵，且是一致的。

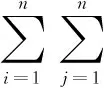
(8)

根据以上定义，主观权重求解步骤为：

(1)根据1～9标度法求判断矩阵A，显然，矩阵A中aij>0，aii=1，且aij=1/aji，互为反矩阵，则B=lg(A)是反对称矩阵。

(2)若C是B的最优传递矩阵，构造矩阵A*=10cij。由上述规定可知，A*是A的最优传递矩阵，并且是一致的。

(3)求A*的最大特征值所对应的特征向量，该特征向量即为所求的主观权重向量。

2.2.3 基于博弈论的融合权重

根据PPA和层次分析法得到水质评价指标的权重后，本文采用融合权重的形式给出最终赋权结果，以此克服主、客观权重的不足。若有x种方法对y个评价指标赋权，权重Wl结果如下

Wl=(wl1,wl2,…,wly)(l=1,2,…,x)

(9)

由博弈论可知，最优赋权结果为

(10)

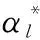
2.3 水质分级云模型实现步骤

首先，根据地下水水体特征拟定相应的评价指标体系和评价标准；在此基础上确定各指标的综合权重，根据云模型正向发生器给出各评价指标在相应等级下的隶属度；最后，由综合权重和隶属度矩阵给出地下水水体的评价结果。水质分级评价流程见图2。

图2 水质分级流程

3 评价结果

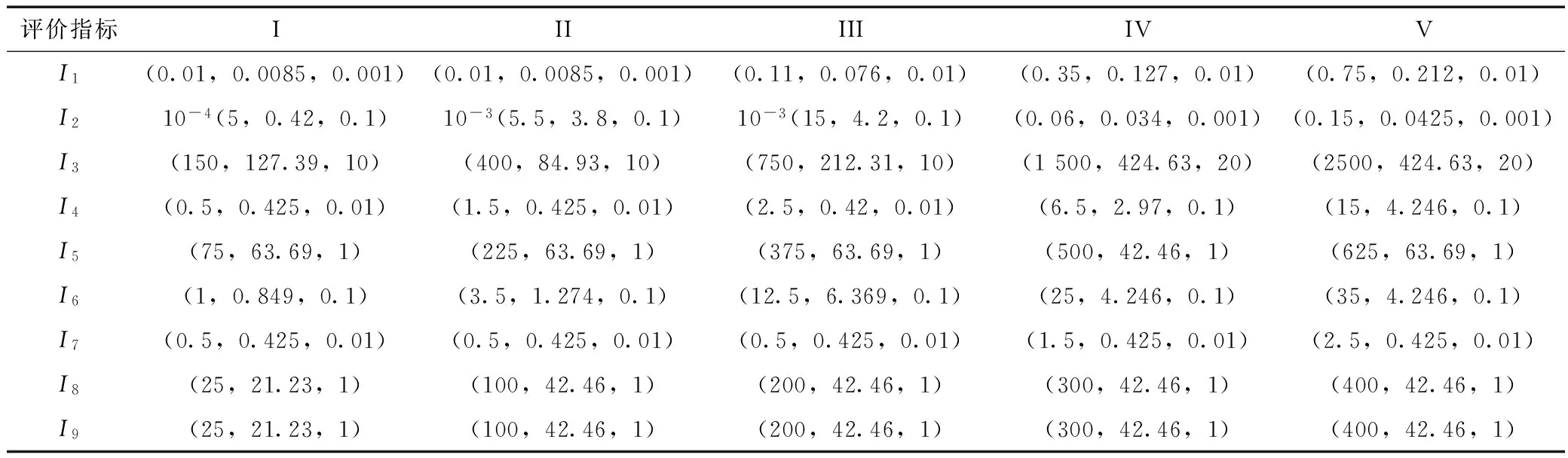
表2为本次水质评价指标体系的云模型特征参数Ex、En和He。表中，指标I1在水质等级I下的数据(0.01，0.008 5，0.001)即为对应的云模型特征参数(Ex，En，He)。其他指标相同。

根据北京市朝阳区19个地下水体监测井的监测数据，同时参考文献[11]，得到本次水质评价指标体系的相关信息(见表3)。

表2 正态云模型特征参数

评价指标IIIIIIIVVI1(0.01,0.0085,0.001)(0.01,0.0085,0.001)(0.11,0.076,0.01)(0.35,0.127,0.01)(0.75,0.212,0.01)I210-4(5,0.42,0.1)10-3(5.5,3.8,0.1)10-3(15,4.2,0.1)(0.06,0.034,0.001)(0.15,0.0425,0.001)I3(150,127.39,10)(400,84.93,10)(750,212.31,10)(1500,424.63,20)(2500,424.63,20)I4(0.5,0.425,0.01)(1.5,0.425,0.01)(2.5,0.42,0.01)(6.5,2.97,0.1)(15,4.246,0.1)I5(75,63.69,1)(225,63.69,1)(375,63.69,1)(500,42.46,1)(625,63.69,1)I6(1,0.849,0.1)(3.5,1.274,0.1)(12.5,6.369,0.1)(25,4.246,0.1)(35,4.246,0.1)I7(0.5,0.425,0.01)(0.5,0.425,0.01)(0.5,0.425,0.01)(1.5,0.425,0.01)(2.5,0.425,0.01)I8(25,21.23,1)(100,42.46,1)(200,42.46,1)(300,42.46,1)(400,42.46,1)I9(25,21.23,1)(100,42.46,1)(200,42.46,1)(300,42.46,1)(400,42.46,1)

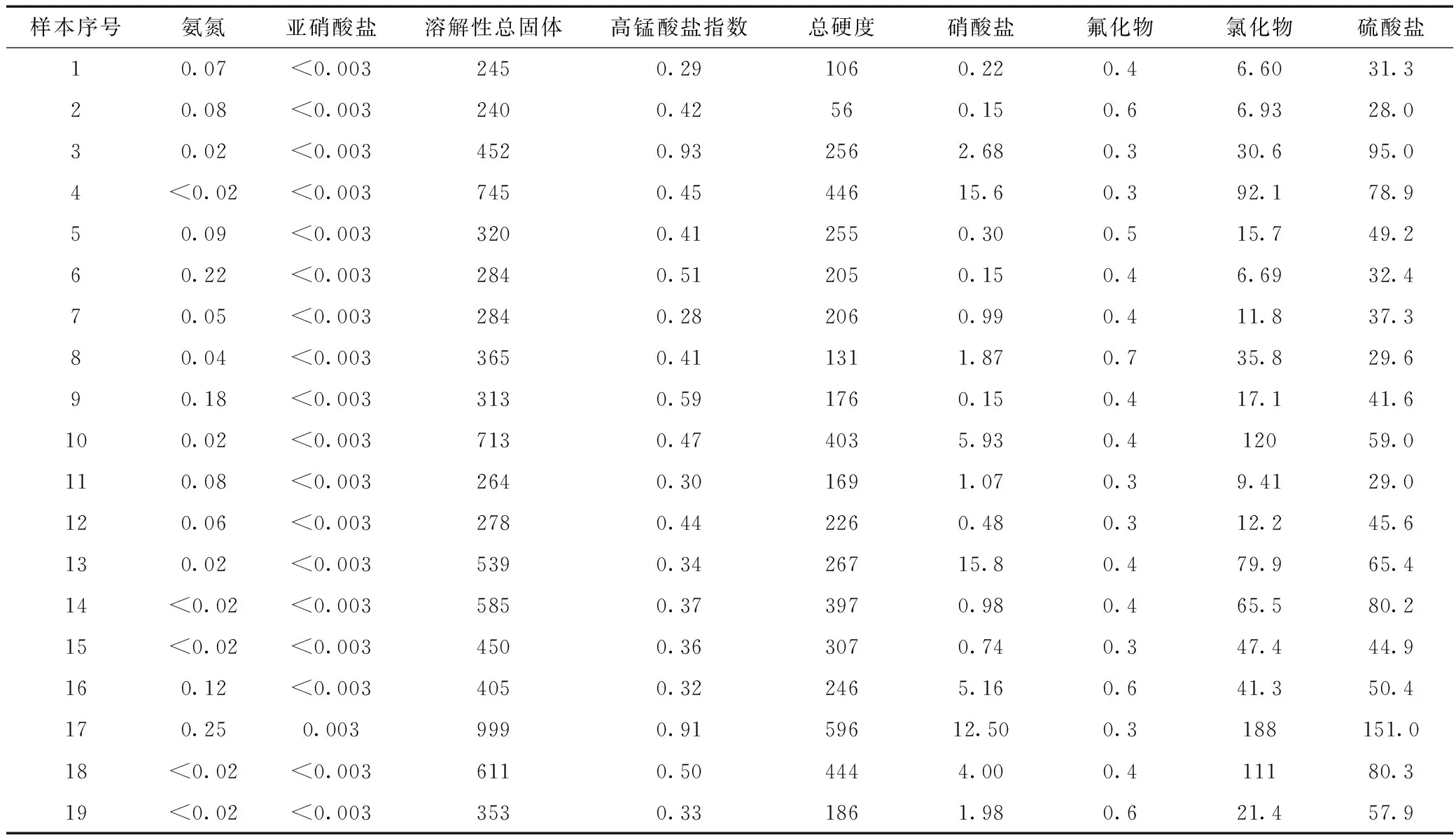
表3 水质指标信息 mg/L

以表2中水质分级综合评价的云模型特征值及表3中水体样本为基础，根据式μ=e-(x-Ex)2/(2En′2)即可计算各指标在相应等级下的隶属度。本次水质分级综合评价中采用Matlab程序完成计算，以1号地下水水体为例，经过程序计算，各指标在相应等级下的隶属度见表4。程序计算时，设置重复计算3 000次，以平均值作为最终的隶属度值。

根据本次水质评价指标体系的相关信息，采用PPA和层次分析法计算各评价指标权重；最后根据融合权重法，得到各指标的综合权重W如下

W={0.103，0.132，0.119，0.125，0.114，0.109,0.099,0.097,0.102}

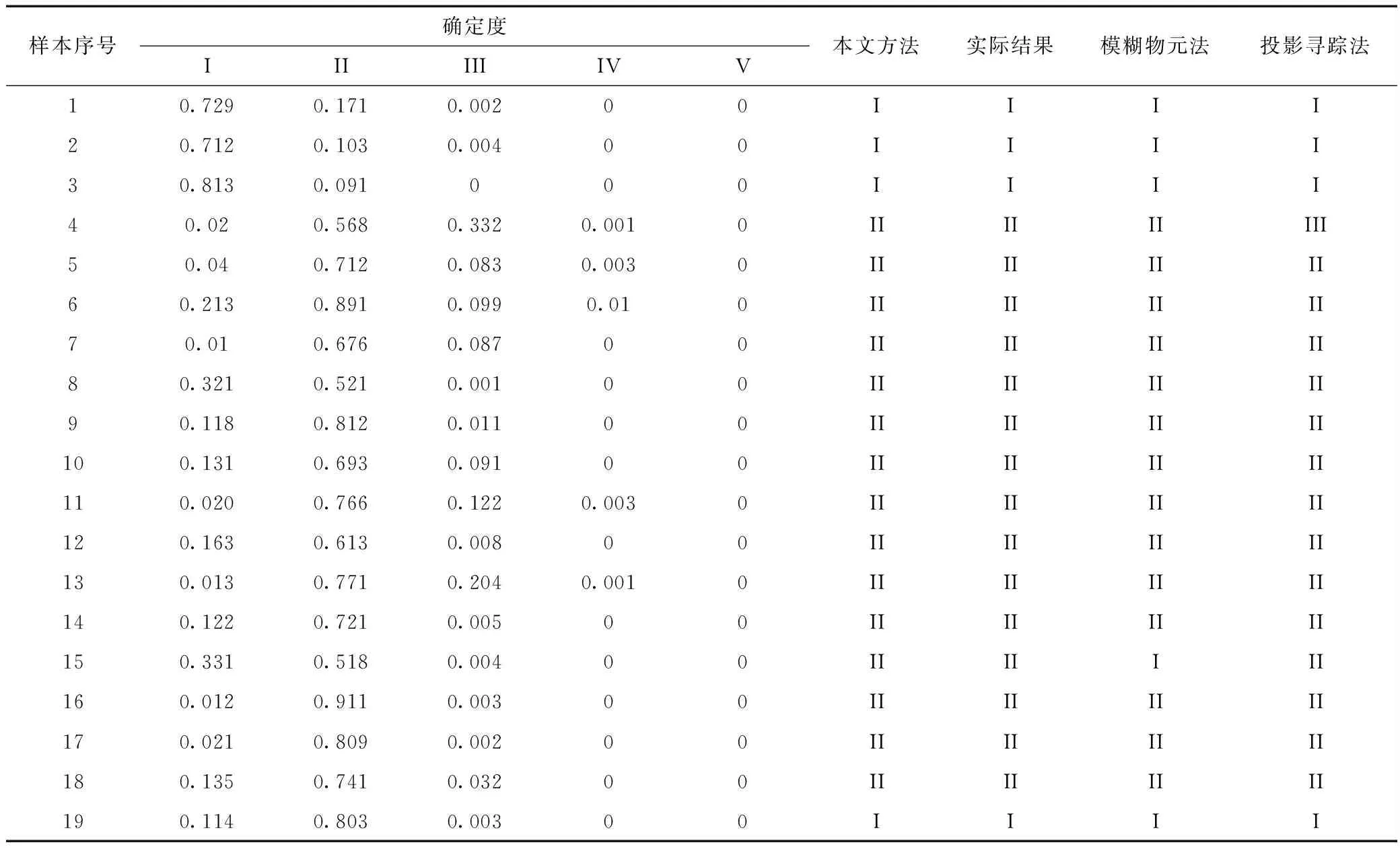
得到水质评价指标体系的隶属度矩阵和权重矩阵后，即可得到各水体样本的水质分级结果。同时，本文还采用模糊物元法和投影寻踪法进行了对比研究。水质评价综合结果见表5。由表5可知，本文方法给出的评价结果精度较高，且与模糊物元法和投影寻踪法给出的评价结果相近。考察4号水体样本可知，投影寻踪法的评价结果出现了一定的偏差，而本文方法未出现差错，故本文方法是一种合理、可行的水质分级模型。

表4 评价指标的隶属度

评价指标IIIIIIIVVI10.7110.2110.00200I20.7150.141000I30.7340.1540.0170.0010I40.7990.189000I50.8510.161000I60.6630.143000I70.7870.197000I80.6580.218000I90.6220.142000

表5 水质评价综合结果

样本序号确定度IIIIIIIVV本文方法实际结果模糊物元法投影寻踪法10.7290.1710.00200IIII20.7120.1030.00400IIII30.8130.091000IIII40.020.5680.3320.0010IIIIIIIII50.040.7120.0830.0030IIIIIIII60.2130.8910.0990.010IIIIIIII70.010.6760.08700IIIIIIII80.3210.5210.00100IIIIIIII90.1180.8120.01100IIIIIIII100.1310.6930.09100IIIIIIII110.0200.7660.1220.0030IIIIIIII120.1630.6130.00800IIIIIIII130.0130.7710.2040.0010IIIIIIII140.1220.7210.00500IIIIIIII150.3310.5180.00400IIIIIII160.0120.9110.00300IIIIIIII170.0210.8090.00200IIIIIIII180.1350.7410.03200IIIIIIII190.1140.8030.00300IIII

4 结 论

本文将正态云模型引入到地下水水体水质综合评价中，拟定了水质分级指标体系和相应指标标准，考虑到云模型可以识别随机性和模糊性的特点，由云模型正向发生器给出评价结果，通过模糊物元法和投影寻踪法对比，证明了本文方法的可行性和合理性。

本次水质综合评价中，提出了一种基于融合权重- 正态云模型的水质分级模型，可以避免水质指标赋权的随机性和盲目性等特点。将该模型应用于北京市朝阳区的地下水水体评价中，评价结果精度较高，可作为一种新的水质分级模型。

[1]尹炜， 辛小康， 梁建奎， 等. 基于主成分分析的丹江口水库支流水质评价[J]. 水电能源科学， 2015， 33(1)： 37- 38．

[2]李济， 李岩， 李德峰. 基于改进AHP法定权的模糊优选模型在地下水质评价中的应用[J]. 华北水利水电学院学报， 2002， 23(2)： 4- 6．

[3]聂青， 纪小敏， 周毅. 基于改进模糊综合评价法的太湖富营养化评价[J]. 水电能源科学， 2015， 33(8)： 29- 32．

[4]谷朝君， 潘颖. 内梅罗指数法在地下水水质评价中的应用及存在问题[J]. 环境保护科学， 2010， 28(10)： 45- 47．

[5]金菊良， 魏一鸣， 丁晶. 水质综合评价的投影寻踪模型[J]. 环境科学学报， 2001， 21(4)： 431- 434．

[6]倪深海， 白玉慧. BP神经网络模型在地下水水质评价中的应用[J]. 系统工程理论与实践， 2000， 20(8)： 124- 127．

[7]贺北方， 王效宇， 贺晓菊， 等. 基于灰色聚类决策的水质评价方法[J]. 郑州大学学报： 工学版， 2002， 23(1)： 10- 13．

[8]邱林， 唐红强， 陈海涛， 等. 集对分析法在地下水水质评价中的应用[J]. 节水灌溉， 2007 (1)： 13- 15．

[9]陈守煌， 于雪峰. 相对隶属度理论及其在地下水水质评价中应用[J]. 辽宁工程技术大学学报： 自然科学版， 2003， 22(5)： 691- 694．

[10]刘章军， 叶燎原. 模糊概率模型及其在地下水水质评价中的应用[J]. 应用基础与工程科学学报， 2007， 15(3)： 286- 293．

[11]巩奕成， 张永祥， 丁飞， 等. 基于萤火虫算法的投影寻踪地下水水质评价方法[J]. 中国矿业大学学报， 2015， 44(3)： 566- 572．

(责任编辑 杨 健)

Study on Water Quality Evaluation Method Based on Combination Weight-Normal Cloud Model

WANG Ruixing

(Vocational and Technical College, Inner Mongolia Agricultural University, Baotou 014109, Inner Mongolia, China)

In view of the uncertainty and ambiguity of groundwater quality evaluation indexes, the combination weight and normal cloud model are combined to establish water quality evaluation combination weight-normal cloud model which is applied in the comprehensive evaluation of groundwater quality. The indicator weight is calculated by using the utility value of data itself which is reflected through combination weight method, that can effectively avoid the difficult of weight allocation. The example calculation results of combination weight-normal cloud model are compared with the results of fuzzy matter element method and projection pursuit method. The comparison verifies that the model is rational, simple and practical．

ground water; water quality evaluation; combination weight; normal cloud model

2015- 12- 28

黑龙江省水利厅科研开发项目(201318)；黑龙江省教育厅科学技术研究项目(11541022)

王瑞星(1983—)，女，内蒙古包头人，讲师，硕士，研究方向为非线性海洋波动动力学．

X824

A

0559- 9342(2016)06- 0005- 05