基于双模式PSO算法求解置换流水车间调度问题

2016-11-22马祎航陶文华

电子设计工程 2016年15期

关键词：双模式惯性流水

马祎航，陶文华，刘阳

（1.辽宁石油化工大学信息与控制工程学院，辽宁抚顺 113000；2.中国石油抚顺石化公司烯烃厂辽宁抚顺 113009）

基于双模式PSO算法求解置换流水车间调度问题

马祎航1，陶文华1，刘阳2

（1.辽宁石油化工大学信息与控制工程学院，辽宁抚顺 113000；2.中国石油抚顺石化公司烯烃厂辽宁抚顺 113009）

针对粒子群算法求解置换流水车间调度这类NP-hard问题存在的早熟问题，本文提出了一种基于随机键编码的双模式飞行粒子群算法。首先，基于ROV规则对工件加工顺序进行随机键编码。其次，粒子在搜索过程中采用带有自适应惯性权重的双模飞行方式来更新位置和速度，避免粒子群陷入早熟收敛状态。为了提高解的质量，每次迭代过程中对PSO优化得到的种群最优解进行邻域局部搜索。最后，通过对标准测试集的数值仿真及与其他PSO算法的比较，证实了所提算法求解该问题的有效性与可行性。

置换流水车间调度；粒子群算法；邻域搜索；随机键

置换流水车间调度问题（Permutation Flow Shop Scheduling Problem，PFSP）是制造系统中重要的规划问题[1]，是在流水车间调度问题的基础上，增加了每台机器加工各工件顺序相同的这一特定的约束条件[2]，已证明3台即为NP-hard问题[3]。许多实际生产过程都可以简化成这类问题，而PFSP的优化研究能够为企业带来更大的生产效益，因此研究PFSP具有重要的理论和实际意义。

求解PFSP的方法主要分为3大类：精确算法、启发式方法和智能算法。虽然理论上精确算法能得到最优解，但其运算时间一般无法接受，因此被用在解决小规模问题。启发式方法根据问题特性，能在较短时间内构造出解，但难以保证解的质量[4]。近年来，随着计算智能的发展，求解PFSP的方法逐步从精确方法和启发式方法发展到智能算法[5]，如遗传算法[6]、量子算法[7]、布谷鸟算法[8]等，尽管这些方法在一些问题上具有良好的收敛性，但在大规模问题上却无法保证解的质量，很容易陷入早熟。

粒子群优化（Particle Swarm Optimization，PSO）算法于1995年由Kennedy和E-berhart提出[9]。它作为一种基于群体的改进启发式算法，尽管已初步成功地用于解决神经网络训练、模糊系统控制和组合优化等问题[10]，但在生产调度方面的研究还是很少的。针对置换流水线调度问题，文中采用基于ROV规则的随机键编码[11]，实现标准PSO操作直接应用在离散优化问题上，而且也保证了解的合法性及解空间的完备性。为了减小陷入局部最优解的可能性，粒子在搜索过程中采用变轨与不变轨双模式飞行并根据群体信息反馈和自身状态选择自己的飞行模式，惯性权重采用自适应线性调节，最后为了提高解的质量，对粒子群算法优化后得到的最优解进行邻域局部搜索。

1 问题描述

置换流水车间调度问题是n个工件在m台机器上的流水加工过程，属于流水车间调度的一类问题，其具有以下特征：

1）每个工件在各机器上加工顺序相同；

2）每台机器上所有工件的加工顺序相同；

3）每个工件在每台机器上只加工一次；

4）每台机器在任意时刻只能加工一个工件。

已知工件在各机器上的准备时间和加工时间，问题目标是寻找一个工件加工顺序，使各工件按该顺序加工的总完成时间（makespan）最小。假设n个工件在m台机器上加工，P为工件i（i=1，2，...，n）在机j（j=1，2，...，m）上的加工时间，C（i，j）为工件i在机器j上的加工完成时间。则C（i，j）的计算公式可描述如下：

2 双模式粒子群算法

2.1 随机键编码

本文对粒子的位置矢量采用基于升序排列规则（Ranked—Order—Value，ROV）的随机键编码实现粒子连续位置到离散值的转换，无需修改PSO算法的进化操作，而且能够保证调度方案的可行性。

ROV规则具体描述如下：对于一个微粒的位置矢量，首先将值最小的分量位置赋予ROV值为1，其次将值第二小的分量位置赋予ROV值为2，依此类推，直到将所有的分量位置都赋予一个唯一的ROV值，从而基于ROV值构造出一个工件排序。以3*4 PFSP为例，已知3个工件在各机器上加工时间为：

假设优化得到第k个粒子的位置为：

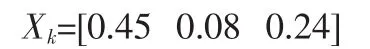
经ROV规则得到一个序列Lk：

按照该序列对工件加工重新排序得：

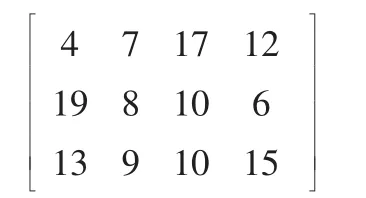
2.2 自适应惯性权重

为了提高算法的收敛稳定性及收敛速度，文中采用一种自适应惯性权重的方法。迭代次数与惯性权重成反比是比较广泛应用的PSO算法惯性权重控制方案：

式中，ω为粒子i在第t次迭代中的取值；Iter为预先设定的最大迭代次数；t为当前迭代数；ωmax为惯性权重最大值，典型取值为0.9；ωmin为惯性权重最小值，典型取值为0.4。

通过全体粒子上一轮迭代结束后适应值的变化来选择惯性权重的取值：

式中，表示粒子i在第i次迭代后的适应值；表示粒子i在第i次迭代后的适应值变化。然后确定各粒子在当前迭代中惯性权重的最终取值：

当t⊂[1，2]时，惯性权重按式（6）取值；当t⊂[3，Iter]时，惯性权重按式（7）、式（8）取值。

2.3 粒子飞行模式

为了提高算法的全局搜索能力，避免过早的陷入早熟，本文采用双模式飞行粒子群算法[12]假设粒子个数为N，第i粒子经过的历史最优位置（i=1，2，…，N）：

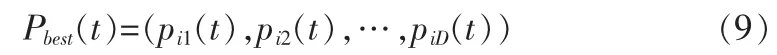
所有粒子经过的最优位置：

分析粒子当前位置的优劣情况：把群体按适应度的大小排序，设粒子群体规模是M，记i粒子t时刻的序号为s（t），此时，s（t）=1表示i粒子t时刻的位置在群体中最优。若s（t）=M则表示i粒子t时刻的位置在群体中最差。粒子依据当前位置优劣情况按式（11）（12）确定飞行模式。

粒子不变轨飞行模式：

粒子变轨飞行模式：

决策因子：

其中，λ服从（0，1）的均匀随机分布，k为[1，2，...，D]的一个随机整数，即i粒子的第d维变轨绕到Gbest（t）的第k维，则称i粒子按变轨飞行模式飞行。DFi（t）为[0，1]的决策因子，它反映i粒子的当前状态，是i粒子确定其下一步飞行模式的依据。适应度最优的决策因子是0，而适应度最差的决策因子是1。换言之，处于较优位置的粒子倾向于选择式（11）的不变轨飞行模式，而处于较差位置的粒子倾向于选择式（12）的变轨飞行。

2.4 邻域局部搜索

在PSO每次迭代优化得到加工顺序之后，通过局部搜索进一步寻找工件加工最佳顺序。文中采用邻域局部搜索方法来确定机器加工序列[13]。步骤如下：1）DMPSO优化后得到所有工件的一个排序β；2）令k=1，取出β中的前2个工件，对两个工件先后加工次序进行评价，选择调度解小的序列作为当前序列；3）令k=k+1，依次将第k个工件插入到当前序列的k个可能的位置，从中选择调度解小的序列作为当前序列；4）重复步骤3），直到β中所有工件均得到新的排序操作。

3 双模式粒子群算法流程图

求解PFSP的双模式粒子群算法（DMPSO）流程如图1所示。

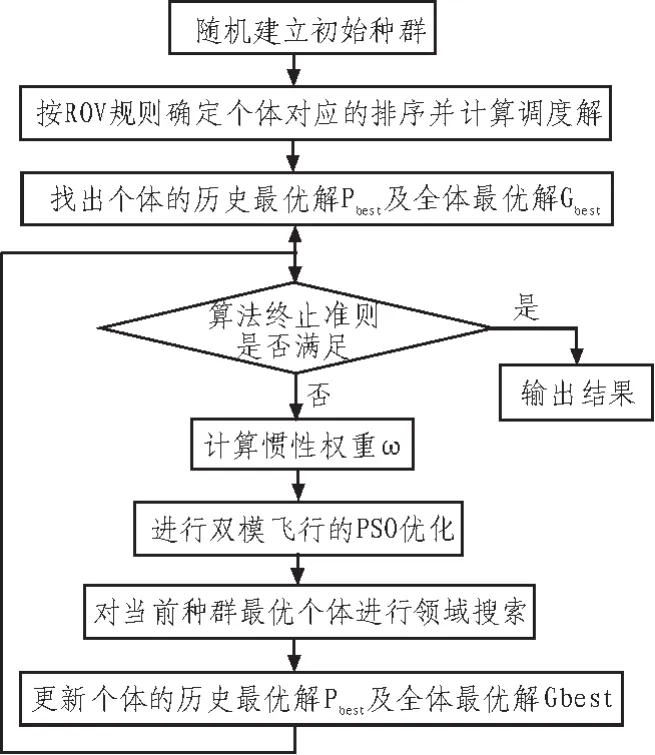
图1 双模式粒子群算法流程图

4 仿真测试与比较

为了验证本文算法求解PFSP的性能，选择Car类[14]和Rec类[15]问题中进行仿真测试。仿真环境：Windows7操作系统，MATLAB2010，处理器2.9 GHz，内存2 GB。参数设置为粒子群算法进化次数M=100，种群规模N=100，加速因子 c1= 1.5，c2=2.5，λ=0.732，粒子位置变化范围为[1，10]。惯性权重ωmax=0.9，ωmin=0.4，c*为问题最优值或目前已知下界值，RE表示算法求出的最优值C与C*相对误差（RE=（c-c*）/c*× 100%），对各类问题独立运行20次得到的平均值，ARE表示平均相对误差。表1为在忽略邻域搜索算法的作用情况下，本文算法与恒定惯性权重DMPSO算法的平均相对误差ARE比较，表2为常规粒子群算法、量子粒子群算法[7]平均相对误差进行对比，图2给出的是DMPSO与PSO两种算法求解Car8的收敛曲线。

图2 求解Car8问题的DMPSO与PSO收敛曲线

1）从表1可知，自适应惯性权重使得算法寻优能力得到很大程度的改善，相对误差减小，

验证了自适应惯性权重对于提高优化算法的稳定性是有效的。

表1 自适应惯性权重对平均相对误差的影响

2）从表2可知，本文算法较其他算法的最优解更能接近已知下界值，反映出PSO粒子飞行模式的改进是有效的。从ARE指标来看，在Car及Rec问题上DMPSO求得的调度解均优于于其他算法，显示出DMPSO在离散空间具有良好的进化机制。在同等规模问题上，ARE相差不大，表明DMPSO算法具有较强的鲁棒性，在求解大规模问题上具有良好的稳定性，能够适用于复杂的生产过程中。从运算速度上来看，DMPSO小于CQPSO，但大于PSO，由于DMPSO是在PSO基础上改进了粒子飞行机制及加入了邻域搜索算法，因此操作复杂度要大于PSO，但相比PSO得到的解，DMPSO能够得到更好的解。

3）由图2可见，DMPSO算法在第41次迭代就得到了最优解，而PSO算法在迭代结束也未能找到最优解，因此DMPSO算法不仅具有较快的收敛性，而且在搜索过程中具有良好的全局搜索能力，保证了求解精度。

5 结论

文中提出的求解置换流水线调度问题的一种改进粒子群算法，通过实验证明了本文提出的改进算法的有效性。经Car和Rec基准问题测试表明本文提出的改进粒子群算法的相对误差远远低于其他粒子群算法，验证了本文算法在求解质量、求解稳定度上的优越性。基于该改进算法的良好性能，下一步研究中，可经过适当改进，将算法运用于解决混合流水线调度问题。

[1]周驰，高亮，高海兵.基于PSO的置换流水车间调度算法[J].电子学报，2006，36(11):2008-2011.

[2]王凌，刘波.微粒群优化与调度算法[M].北京:清华大学出版社，2011.

[3]Garey M R，Johnson D S，Sethy R.The complexity of flowshop and job-shop scheduling[J].Mathematics of Operations Research，1976，1（2）:117-129.

[4]郑晓龙，王凌，王圣尧.求解置换流水线调度问题的混合离散果蝇算法[J].控制理论与应用，2014，31（2）:159-164.

[5]于承敏，郑丽萍.PSO算法求解PFSP问题研究进展[J].哈尔滨理工大学学报，2012，17（6）:14-20.

[6]李小缤，白焰，耿林霄.求解置换流水车间调度问题的改进遗传算法[J].计算机应用，2013，33（12）:3576-3579.

[7]杨子江，顾幸生.基于混沌量子粒子群算法的置换流水车间调度[J].华东理工大学学报：自然科学版，2013，39（3）: 325-331.

[8]刘长平，叶春明.求解置换流水车间调度的布谷鸟算法[J].上海理工大学学报，2013，35（1）:17-20.

[9]Kennedy J，Eberhart R C.Particle swarm optimization[C].// Proceedings of International Con-ference on Neural Networks.Piscataway，N.J.USA:IEEE Press，1995:1942-1948.

[10]于承敏，郑丽萍.PSO算法求解PFSP问题研究进展[J].哈尔滨理工大学学报，2012，17（6）:17-20.

[11]王凌.车间调度及其遗传算法[M].北京:清华大学出版社，2003.

[12]李景洋，王勇，李春雷.采用双模飞行的粒子群优化算法[J].模式识别与人工智能，2014，27（6）:533-539.

[13]潘全科，高亮，李新宇.流水车间调度及其优化算法[M].华中科技大学出版社，2013.

[14]Carlieb J.Ordonnancements à contraintes disjonetives[J].RAIRO-Operations Research-Recherche Opérationnelle.1978，12（4）:333-350.

[15]Reeves C R.A genetic algorithm for flow-shop sequencing[J].Computers and Operations Research 1995，22（1）:5-13.

Dual mode PSO for solving permutation flow shop scheduling problem

MA Yi-hang1，TAO Wen-hua1，LIU Yang2
（1.School of Information and Control Engineering，Liaoning Shihua University，Fushun 113000，China；2.Olefins plant of China Petroleum Fushun Petrochemical Company，Fushun 113009，China）

Our objective in this report is to study the permutation flow shop scheduling problem，this paper proposes a dualmode particle swarm optimization algorithm based on random key code.Based on the ROV rules for random code for the processing sequence；Secondly，particles in the search process use dual flight mode with the adaptive inertia weight to update the position and velocity，avoid particle swarm into premature convergence；In order to improve the quality of the solution，in each iteration the neighborhood local search algorithm is used on PSO optimized solution.Finally a comparison through numerical simulation and comparison of different PSO algorithm on the standard test set，to verify the feasibility and effectiveness of the proposed algorithm to solve the problem.

permutation flow-shop scheduling；particle swarm optimization；neighborhood search；random key