基于模糊控制的气体扩散模型选择
2016-11-22邓振文孙启湲贾云伟
邓振文 孙启湲 贾云伟
(天津理工大学天津市先进机电系统设计与智能控制重点实验室,天津 300384)
基于模糊控制的气体扩散模型选择
邓振文 孙启湲 贾云伟
(天津理工大学天津市先进机电系统设计与智能控制重点实验室,天津 300384)
提出一种气体扩散模型的选择方法,可应用于有害气体泄漏源的发现和搜寻。比较模糊控制原理的优点,再优化部分学者提出的气体扩散模型,设计出气体扩散模型选择的模糊推理系统。该系统可根据对环境的测量数据推理出适合特定环境条件下的气体扩散模型。在模糊推理系统中,由传感器测量的环境数据作为输入量导入模糊控制器,经Mamdani模糊算法,最终导出的输出量即某一气体扩散模型。使用Matlab中的模糊控制工具箱(Fuzzy)对模糊推理系统进行仿真实验,结果表明:不同气体在不同环境条件下的气体扩散模型能够通过模糊推理得到,说明该方法可行。
模型选择 模糊控制 有害气体 扩散模型
易燃、易爆、有毒物质的泄漏会产生严重的后果[1],因此气体扩散研究逐渐受到广泛重视。气体扩散模型的研究发展于20世纪,主要研究某种气体在大气中的扩散状态。在进行气体扩散模拟时,常采用单一的气体扩散模型预测环境各位置处的浓度信息,以对泄漏物排放进行控制[2,3]或对重污染区域做出预警[4]。但是,对于在未知环境下有害气体泄漏源参数估计的研究[5,6],使用单一气体扩散模型将存在局限性。因为不同大小的分子在空气中的扩散形式不同且气体在大气中的扩散具有很多影响因素[7],包括风速、温度、湿度及太阳辐射等,这些因素将影响泄漏源参数的估计精度,从而导致结果产生较大的误差,严重影响后续研究(如有害气体泄漏源的搜寻)甚至造成后续研究失败。所以有必要结合实时大气环境条件,选择出最匹配的气体扩散模型。由于从多方面对事物进行评价难免带有模糊性和主观性,采用模糊数学的方法进行综合评价将使结果尽量客观,从而取得更好的实际效果[8~10]。因此笔者引入控制领域的模糊控制原理,使模型选择系统具备自我推理能力,能够从模型库中推理出最优的气体扩散模型。
1 模糊控制理论
模糊控制实质上是一种非线性控制,从属于智能控制的范畴,广泛应用于自动化领域。一个基本的模糊控制器包括3部分:模糊化、模糊推理和反模糊化[11]。图1为一个多输入单输出(MISO)的模糊控制器。
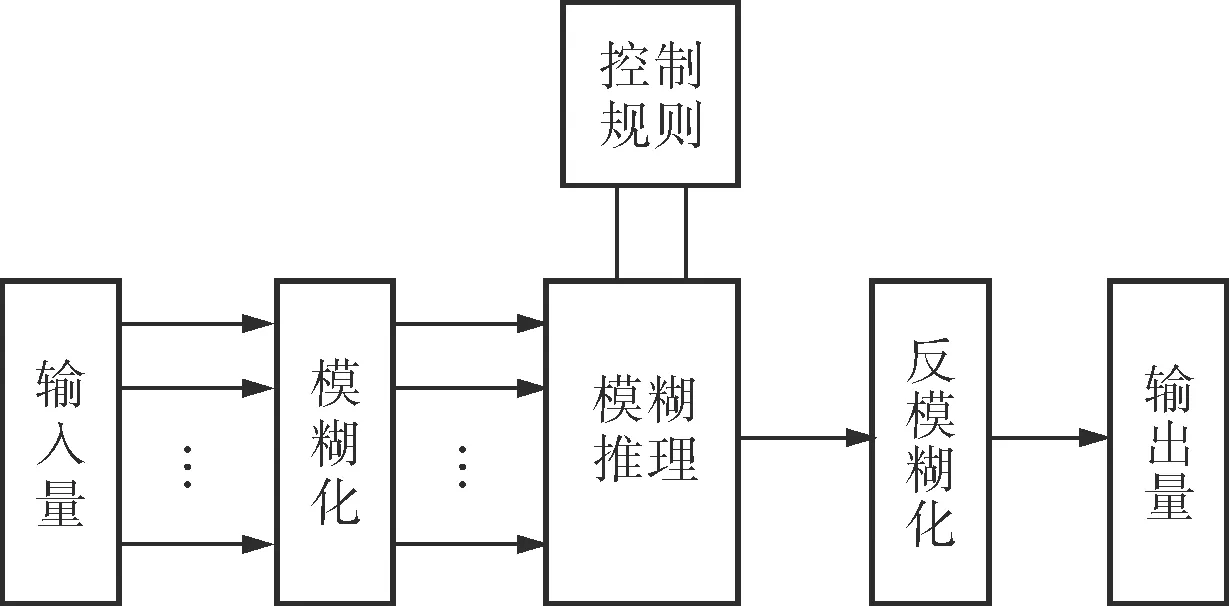
图1 模糊控制器的结构框图
模糊化是将客观上的精确量转化为带有模糊性的模糊量,反映了环境测量数据u对该输入量论域U中模糊集合F的隶属度,由隶属度函数μF(u)来表示。
模糊推理是在有限控制规则的基础上进行模糊推理和运算。常采用较为传统的Mamdani推理。多输入单输出的模糊规则形式为:

(1)
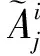
按Mamdani推理,每条模糊规则为直积空间X1×X2×…×Xn×Y上的一个模糊关系:
(2)
N条模糊规则全体构成的模糊关系为:
(3)
对于一组输入值,模糊推理的结论为:
(4)
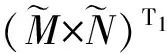
反模糊过程是从模糊推理得到的模糊集合,使用模糊输出的隶属度函数找出一个最能代表这个模糊集合和模糊控制作用可能性分布的精确量。
2 气体扩散模型
大气环境复杂多变,这对气体扩散模型的研究带来很大的困难。经过长期的发展,出现很多气体扩散模型和模型修正参数,可近似估计扩散的结果。几类常见的气体扩散模型有静风扩散模型、高斯模型、BM模型、Sutton模型和FEM3模型[7,12],这几类气体扩散模型的比较见表1。

表1 常见气体扩散模型的比较
其中,静风扩散模型适合无风环境下的气体扩散研究,较常见的模型有高斯扩展模型[1]、A-Fick无风扩散模型[13]、半球扩散模型[14]和室内无风扩散模型[15],笔者在模糊推理系统中对静风扩散模型将不进行细化;高斯模型包含高斯模型烟羽模型和高斯烟团模型,开发较早,经过后期的发展技术逐渐成熟,在许多特定环境下提供了大量的可选参数[2],例如稳定度系数C和扩散范围修正参数,使模型可应用于不同气候下高架和平地的连续点源扩散。但是两者均未考虑重力的影响,因此只适用于轻气体或与空气密度相近的气体扩散;Sutton模型是用湍流扩散统计理论来处理湍流扩散问题的,而湍流环境较复杂,最突出的特点是风速和风向的突变以及局部温度大范围波动。表1中的扩散模型多数采用关系表达式和经验性扩散参数描述,所以计算量较小且精度一般;而FEM3计算公式复杂,对连续源和瞬时源稍加变动后都可以模拟,精度较好,但可能会因计算量大而影响数据的实时性。
3 气体扩散模型的模糊推理系统设计
笔者提出一种方法,引用控制工程领域的模糊推理原理,根据现有的专家知识和经验,从模型库中推理选择出合适的气体扩散模型。即使现有的传感器数据存在误差,模糊推理也能做出最佳的判断,从而减少人工判断的误差。Matlab提供一个功能强大的模糊控制工具箱(Fuzzy)且具备较好的兼容性,可实现对系统的仿真实验,又提供接口可简便地与C++、Java等编程语言形成对接,利于软件开发、机器人控制等研究。笔者将借助Matlab的模糊控制工具箱创建一个模糊控制器,利用一些常用传感器获取部分环境数据,通过这些数据,对几种常见的有害气体扩散模型进行模糊推理,最后得到较为合理的气体扩散模型,流程如图2所示。
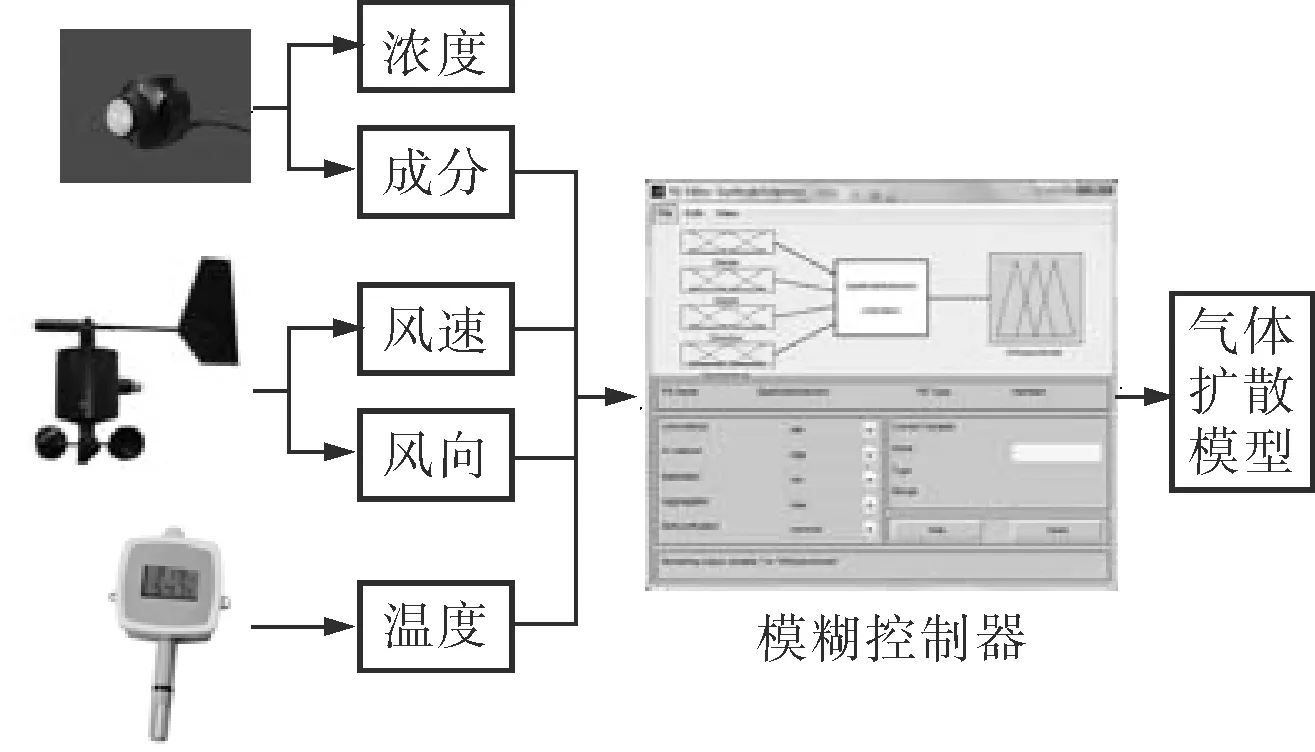
图2 气体扩散模型选择流程
对于常见的气体扩散模型,最主要的区别是密度。密度不同,将直接影响扩散的方式,轻气上浮,中气均匀扩散,重气下沉[16]。为了更好地辨别大气中的气体成分(尤其是有害气体),可采用近红外光谱分析技术[17]。该技术包含定性分析和定量分析,定性分析的目的是确定物质的组成与结构,可确定气体的成分,而定量分析则是为了确定物质中某些组分的含量或是物质的品质属性的值,可确定气体的浓度。对于已知的泄漏气体可采用超声技术测量气体的浓度[18]。
此外,风速也是选用气体扩散模型的重要影响因素。风速能加快风向一侧的有害气体扩散,而抑制背风一侧。在软风环境下,风速对于气体扩散影响较小,可等同于静风扩散;反之,风速较大时,风速的影响将大于分子的自身运动,此时分子的自身运动将忽略不计。风向的变化率也可近似地衡量大气湍流运动程度。温度的高低直接影响气体分子的扩散速度,很大程度上决定大气的稳定程度,也是近似衡量大气湍流运动的因素之一。
模糊控制器中需要设置相应输入量和输出量的变量和隶属度函数。Dense表示所测有害气体的密度,Speed表示大气中的风速,Direction表示风向的变化率,Temperature表示大气中的温度,Model表示气体扩散模型。模糊控制器中设定Dense的论域以空气的密度(1.29kg/m3)为基准,分为TL、L、ZE、H、TH共5个模糊状态;Speed的论域为0~10m/s,分为ZE、S、M、F、TF共5个状态;Direction的模糊状态为ZE、S、F;Temperature的论域为-20~40℃,分为TC、C、WM、H、TH共5个模糊状态;Model分为A、B、C、D、E,分别对应静风模型、高斯模型、Sutton模型、BM模型和FEM3模型。
在制定模糊控制规则时,需参考有经验的操作者或专家的控制知识和经验。可参考以下几点:
a. 根据特定地区气候的特点,适当选择气体扩散模型作为模型库。
b. 了解气体分子运动规律,适当调整模糊规则。如温度越高的环境下,气体分子越活跃,静风模型的临界风速应适当增大。
c. 优先选用高斯模型。高斯模型参数较完善,条件相似情况下,宜尽量选用高斯模型。
d. 对于较极端环境,优先选择模拟效果较好的气体扩散模型。如湍流程度较大的情况下,应优先选择Sutton模型。
模糊控制器中包含4个输入量和一个输出量,共23个模糊变量,将产生375条模糊控制规则语句。三角形隶属度函数对于各变量赋予的隶属度比较均匀,可使模糊系统更加平稳,所以全部变量将采用三角形隶属度函数。各模糊变量的隶属曲线根据扩散特点也进行特殊的调整。各隶属度函数如图3~7所示。
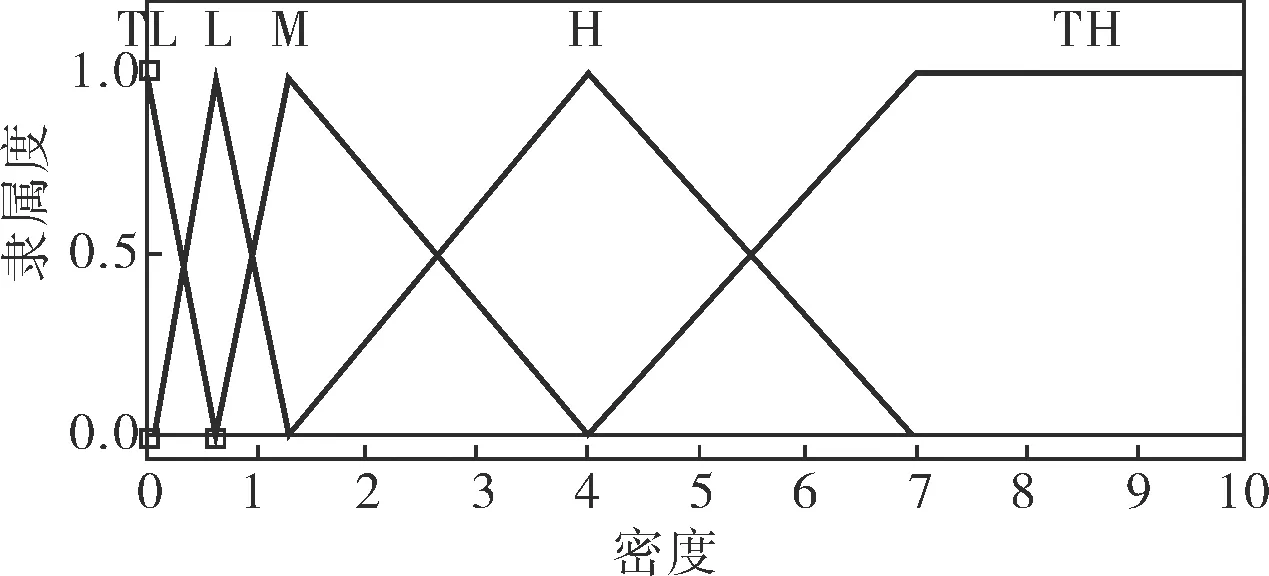
图3 被检测气体密度Dense的隶属度函数
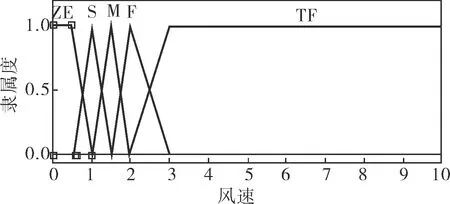
图4 大气风速Speed的隶属度函数

图5 大气风向Direction的隶属度函数
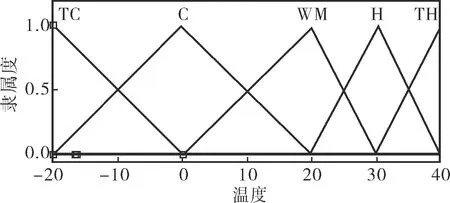
图6 大气温度Temperature的隶属度函数

图7 气体扩散模型Model的隶属度函数
4 仿真实验
选择CO(密度1.25kg/m3)在风速为2m/s、风向变化较小(0.3)、常温(20℃)环境下的气体扩散模型。在模糊控制器中输入上述各参数的值[1.25 2 0.3 20],输出结果为0.25,对应的扩散模型为高斯模型(B),仿真结果如图8所示。
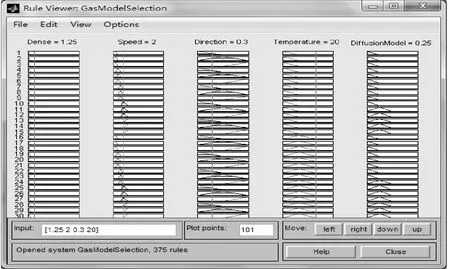
图8 仿真结果
选择Cl2(密度3.21kg/m3)在风速为4m/s、风向变化偏小(0.4)、高温(35℃)环境下的气体扩散模型。输入参数[3.21 4 0.4 35]至模糊控制器中,输出结果为0.559,由最大隶属度法[8]得到对应的扩散模型为Sutton模型(C)。
实验表明,模糊推理可迅速地推理出适合特定环境条件下某种气体(尤其是有害气体)的扩散模型。避免了人工选择产生的误差,同时提高了运算效率,能够满足有实时性要求的场合。
5 结束语
笔者提供了一种气体扩散模型的选择方法,将控制领域的模糊推理原理应用于气体扩散模型的选择。在系统设计中,选用常见的模型作为模型库,主要的环境数据作为衡量参数,结合部分学者的经验调整各变量的隶属度函数。实验证明,模糊控制可作为一种有效的工具,在传感器获取环境信息后,有效选择较合适的气体扩散模型。在气体扩散模型选择系统设计中也存在一些不足,例如,各变量的隶属度函数未达到最优;气体扩散模型库还需要全面补充;模糊规则需涵盖大部分学者经验等。
[1] 高万东.液化气体汽车罐车定期检验的安全控制[J].化工机械,2012,39(3):391~392.
[2] 童志权.大气污染控制工程[M].北京:机械工业出版社,2006:372~412.
[3] Chambers S D,Williams A G,Crawford J,et al.On the Use of Radon for Quantifying the Effects of Atmospheric Stability on Urban Emissions[J].Atmospheric Chemistry Physics,2015,(15):1175~1190.
[4] 肖微炜,赵永欣,张以飞,等.基于GIS的重气体扩散预测模拟研究[J].环境科学与管理,2014,39(2):104~107.
[5] 邵昀明,朱鹰,黄德先,等.有毒气体扩散源参数估计方法综述[J].化工学报,2011,62(10):2677~2681.
[6] Benkherouf A,Allidina A Y.Leak Detection and Location in Gas Pipelines[J].Control Theory and Applications,IEE Proceedings D,1988,135(2):142~148.
[7] 丁信伟,王淑兰,徐国庆.可燃及毒性气体扩散研究[J].化学工程,2000,28(1):35~38.
[8] 曹茹.基于模糊综合评判的冷却装置选型设计[J].化工机械,2011,38(1):11~13.
[9] 孙振国,顾伯勤.螺栓法兰连接模糊可靠性数值计算方法[J].化工机械,2014,41(5):647~651,686.
[10] 郭凡,於孝春,袁东明.基于模糊FMEA的环己酮肟重排反应器风险分析[J].化工机械,2015,42(1):6~10,15.
[11] 李少远.智能控制[M].北京:机械工业出版社,2009:64~68.
[12] 王治华.受限空间内气体扩散的数值模拟及分析[D].大连:大连理工大学,2009.
[13] 龙长江,齐欢,张翼鹏.煤气储罐泄漏扩散模型及仿真[J].华中科技大学学报,2006,34(4):42~44.
[14] 黄德寅,孙金艳,于信波.半球扩散模型在氨中毒职业病危害事故风险评估中的应用[J].职业卫生与应急救援,2005,23(3):141~142.
[15] 于畅,田贯三.可燃气体室内泄漏扩散的研究[J].山东建筑工程学院学报,2006,21(3):243~247.
[16] 奚旦立.突发性污染事件应急处置工程[M].北京:化学工业出版社,2010:74~93.
[17] Dantasa H V,Barbosaa M F,Nascimentob E C L,et al.Screening Analysis of Natural Gas with Respect to Methane Content by Near-infrared Spectrometry[J].Microchemical Journal,2014,114:210~215.
[18] 蔡艺剧,黄勇,尹遴,等.一种新的微量气体浓度检测方法[J].化工自动化及仪表,2012,39(4):477~479.
SelectionofGasDiffusionModelBasedonFuzzyControl
DENG Zhen-wen, SUN Qi-yuan, JIA Yun-wei
(TianjinKeyLaboratoryofDesignandIntelligentControlofAdvancedMechatronicsSystem,TianjinUniversityofTechnology,Tianjin300384,China)
A method of selecting gas diffusion model was proposed and applied to discovering source of leaks of the harmful gas. Through comparing advantages of fuzzy control theory and optimizing the gas diffusion model proposed by some scholars, a fuzzy inference system for selecting gas diffusion model was designed to work out a gas diffusion model suitable for special environmental conditions based on the environmental data measured. In this fuzzy inference system, the environmental data measured by the sensor can be led into the fuzzy controller as an input variable for fuzzy reasoning through Mamdani fuzzy algorithm; and in this operation, the output variable derived at last is the gas diffusion model requested. Simulating this fuzzy inference system with fuzzy control toolbox in Matlab shows that the gas diffusion model for different gases under various environmental conditions can be reached through the fuzzy inference and it testifies the feasibility of this method.
model selection, fuzzy control, harmful gas, diffusion model
TH865
A
1000-3932(2016)03-0258-05
2015-05-01(修改稿)
国家自然科学基金资助项目(61201081)
