单壁碳纳米管改变手性外延生长的密度泛函理论研究

谌 为， 李 峰， 刘 畅， 尹利长

(中国科学院金属研究所 沈阳材料科学国家(联合)实验室，辽宁 沈阳110016)



单壁碳纳米管改变手性外延生长的密度泛函理论研究

谌 为， 李 峰， 刘 畅， 尹利长

(中国科学院金属研究所 沈阳材料科学国家(联合)实验室，辽宁 沈阳110016)

采用密度泛函理论计算系统研究了单壁碳纳米管(Single-walled carbon nanotube，SWCNT)改变手性外延生长(手性指数从(n,m)变化到(n±Δ,m∓Δ)，其中Δ=1和2)的热力学过程。结果表明，碳管手性变化后外延生长在热力学上都需要吸收能量，其所需吸收的能量随着管径的减小线性减小。在Δ=1的情况下，由于近扶手椅型碳管改变手性时，所引入的5～7元环对与管轴的夹角比近锯齿型碳管更大，导致5～7元环对的形成能增加，使得管径相同的近扶手椅型碳管比近锯齿型碳管在改变手性生长时需要吸收更多的能量。在Δ=2的情况下，发现只有当两个必须引入的5～7元环对相互毗邻，手性改变的外延生长所需能量最小，预测其为实验上最易于实现的碳管手性指数由(n,m)变化到(n±Δ,m∓Δ)的外延生长模式。这些理论研究结果有助于深入理解SWCNTs手性变化后外延生长的热力学行为，可为基于外延生长可控制备单一手性SWCNTs提供理论依据。

单壁碳纳米管； 手性变化； 5～7缺陷； 外延生长； 密度泛函理论

1 Introduction

A single-walled carbon nanotube (SWCNT) can be conceptually considered as a cylinder rolled up from a graphene sheet. The geometry structure of a SWCNT is exclusively determined by a pair of chirality indices (n,m) according to the rolling direction of the graphene sheet[1]. The electronic properties of SWCNTs are closely related to their geometry structures. For example, SWCNTs can be either metallic (m-SWCNTs) or semiconducting (s-SWCNTs) depending on their chiralities. To be specific, when (2n+m)/3 is an integer, the SWCNTs are metallic, and otherwise semiconducting[2]. The unique electronic properties of SWCNTs show appealling potential applications in many fields. For instance, s-SWCNTs can be used for high mobility nano transistors[3]and computers[4], while m-SWCNTs are suitable for fabricating transparent electrically conductive films[5], field-emission electron sources[6], nanocables[7], and so on. Unfortunately, as-grown SWCNT samples are always a mixture of m-SWCNTs and s-SWCNTs[8]due to the negligible formation energy difference among different SWCNTs with comparable diameters[9], highly limiting their widespread applications. Basically, the above issue can be possibly solved by a direct synthesis of uniformly metallic (or semiconducting) or even single-chirality nanotubes through controlling the composition, morphology and/or size of catalysts for SWCNT growth by chemical vapor deposition[10]. For example, dominantly semiconducting SWCNTs with a narrow distribution of diameter and chirality were synthesized by using bimetallic CoMn[11], FeRu[12]catalysts, or monometallic Co nanoparticles with a well-defined crystal structure[13]. Moreover, SWCNTs with only a few specific chiralities were realized by a fine regulation and design of catalysts[14-20]. Also, the chirality distribution of as-grown SWCNTs can be altered by varying the composition of NixFe1-xnanocatalysts based on an epitaxial growth model[21]. Very recently, Yang et al. reported a direct growth of the (12,6) tube with an abundance higher than 92% using WCo bimetallic nanocatalysts[22], and Fasel et al. have achieved single-chirality SWCNTs with only one chirality of (6, 6) by using surface-catalyzed cyclodehydrogenation of C96H54precusors on Pt(111) surface[23]. However, despite enormous efforts and remarkable progress, real achievements of uniformly conducting and even chirally pure SWCNTs in a large amount by a direct growth is still highly impractical due to the insufficient understanding of the growth mechanism and the multiple factors (catalyst structure and morphology[24], temperature[25], and so on) relating to the growth of SWCNTs.

On the other hand, we also noted that the chirality of SWCNTs could be uniformly controlled by an epitaxial growth with open-end short SWCNT seeds, namely “cloning growth”. For example, Yao et al. grew SWCNTs with a controlled chirality by using open-end SWCNTs as seeds[26], Liu et al. synthesized SWCNTs with predefined chiralities using purified single-chirality nanotubes as seeds[27]. It is also found that the diameter or even the chirality of SWCNTs can be finely controlled via a tube junction formation by changing the temperature during SWCNT growth[28], which is a typical case for a chirality-changed. In principle, such a chirality-unchanged (cloning growth) or chirality-changed epitaxial growth would achieve a chirally pure SWCNT growth in a large amount with finely controlled growth conditions. However, the underlying mechanism of this cloning or chirality-changed epitaxial growth of SWCNTs is still unclear, thus highly hindering the experimental progress in this aspect.

In this work, we systematically studied the thermodynamics for the cloning and chirality-changed growth of SWCNTs by DFT calculations, aiming to obtain guideful hints to achieve single-chirality SWCNTs by an epitaxial growth. Taking the SWCNTs with diameters ranging from 0.4 to 1.3 nm as examples, we have calculated the energy changes (ΔE) for SWCNTs with chirality change from (n,m) to (n±Δ, m∓Δ),Δ=1 and 2. The energy changes for the chirality-changed epitaxial growth of SWCNTs increase linearly with increasing the tube diameters, ranging from 1.1 (2.0) to 3.7 (4.4) eV in the case ofΔ=1 (2). It is also found that the energy changes in the case ofΔ=1 are about 0.2- 0.4 eV larger for near armchair (nAC) tubes than those for near zigzag (nZZ) tubes, resulting from the larger angle difference between pentagon-heptagon defects (5,7-defects) and the tube axis for nAC tubes. In the case ofΔ=2, the topological connection with two adjacent 5,7-defects, which are indispensable for the chirality-changed growth of SWCNTs in this case, is found to be the most energetically stable. Similar to the case ofΔ=1, the energy needed to change chirality of a SWCNT forΔ=2 case increases with increasing the tube diameter. Our DFT results provide a deep understanding on the thermodynamics of the chirality-changed epitaxial growth and may guide for the chirality-controlled synthesis of SWCNTs.

2 Computational methods

In this work, all calculations were carried out within the framework of DFT implemented in the Vienna Ab Initio Simulation Package (VASP)[29], using the generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof[30]. The electron-ion interactions were described by using the frozen-core projector augmented wave approach[31, 32]. Testing calculations show that the total energy of a (5, 1)/(4, 2) tube junction obtained by using a cut-off energy of 450 eV is only 30 meV lower than that by using the cut-off energy of 280 eV, which is negligible in comparison with the energy input (1.1 eV) for changing a (5, 1) tube to a (4, 2) tube. Thus, the energy cut-off for plane waves was set to be 280 eV for all calculations in this work. Considering that different tube junctions were constructed based on the cluster model to simulate the chirality-changed epitaxial growth for different SWCNTs, only Gamma point was used to sample the first Brillouin zone for all calculations in this work. Optimized geometry structures for all tube junctions considered in the present work were determined until the residual forces acted on each atom were less than 0.01 eV/Å.

Different tube junctions consisting of two short segments of different SWCNTs with chirality of (n,m) and (n±Δ, m∓Δ) (Δ=1, 2) were constructed to study the atomic structure change and corresponding energy change induced by the chirality-changed epitaxial growth of different SWCNTs. Eight nZZ (n, 1) (n=5-11 and 15) and eight other tubes including (5,2), (5,3), (6,3), (6,4), (7,4), (7,5), (8,5) and (10,7) were considered for the case of chirality change withΔ=1, and twelve (n,m) tubes with m=2, 3, 4 and n ranging from m+4 to m+7 for case of chirality change withΔ=2, in order to achieve a convincing comparison of the energy change among different tubes in this work. It should be noted that, one of the initial purposes of this work is to understand the difference of energy changes between highly symmetrical tubes, like ZZ and AC tubes, during their chirality-changed epitaxial growths. Unfortunately, both ZZ and AC tubes will change their helicities from the left-handed to the right-handed (or from right-handed to left-handed) when their chiralities are changed from (n,m) to (n±Δ, m∓Δ) (Δ=1, 2). Alternatively, we choose these nZZ and nAC tubes in this work without considering the possible influence of the tube helicity on the energy changes during the chirality-changed epitaxial growth. We use the cluster models for all the calculations in this work since the periodic models for a tube junction are too large for standard DFT calculations, and a large supercell containing a short tube (or a tube junction) was constructed to model the chirality-changed epitaxial growth of SWCNTs. The inter-tube distance was set to be 10 Å to minimize the periodic image interactions for all calculations. For comparison, a monolayer graphene sheet with a 5,7-defect (or two 5,7-defects) was constructed to model the hypothetically chirality-changed growth of a SWCNT with an infinite diameter.

3 Results and discussion

It is intuitively easy to understand that the cloning growth of a SWCNT just grows the tube length along the direction of the tube axis by continuously adding carbon atoms at the open-end without inducing any defects, while the chirality-changed epitaxial growth for the SWCNTs inevitably induces topological defects at the tube junction position to change the tube chirality of (n, m) to (n′, m′). As for the chirality-changed epitaxial growth considered in this work, we only focus on the cases in which the tube diameters do not change too much, for example from (n, m) to (n±Δ, m∓Δ) withΔ=1 and 2, since it is very difficult to enlarge or reduce the tube diameters in a typically epitaxial growth without catalyst at the open-end. As well demonstrated, at least one and two pentagon-heptagon topological defects have to be introduced for the (n,m)/(n±1, m∓1) and (n,m)/(n±2, m∓2) tube junctions, respectively[33]. In energetics, the topological 5,7-defects in sp2carbon materials like graphene and carbon nanotubes contribute the minimum energy gain to the total energy due to the zero net curvature change, which has been proved to be the dominant and thermodynamically favorable defects in the SWCNT junctions[34-36]and graphene grain boundary[37-39]. Following the rule proposed in ref. 31, the tube junctions of different SWCNTs with chirality changed from (n,m) to (n±1, m∓1) and from (n, m) to (n±1, m∓1) can be easily constructed.

Fig. 1 presents the fully relaxed atomic structures of four tube junctions showing the chirality change for (10, 1) and (7, 5) tubes from (n, m) to (n±1, m∓1). As clearly shown in Fig. 1, by inducing only one 5,7-defect, the tube chirality changes from initial (n, m) to (n±1, m∓1) without an obvious diameter change for both (10, 1) and (7, 5) tubes. And such a topological 5,7-defect connects two tube segments with different chiralities, thus forming a tube junction.

We expect that different SWCNTs need different energies to change their chiralities during the epitaxial growth. In order to check this, the energies needed for changing the chiralities of different SWCNTs are calculated based on the following equation,

ΔE=(2×E(n1,m1)→(n2,m2)-E(n1,m1)-E(n2,m2))/2

(1)

where,E(n1,m1)→(n2,m2) is the total energy of an isolated tube junction of (n1,m1)/(n2,m2),E(n1,m1) andE(n2,m2) are the total energies of the correponding and defect-free SWCNTs with chiralities of (n1,m1) and (n2,m2), respectively. Therefore, the enengy (ΔE) needed for the chirality-unchanged epitaxial growth of a SWCNT should be zero according to Eq. (1). It should be also noted that the number of C and H atoms in an isolated tube junction should be exactly the same as the half number of C and H atoms in two corresponding SWCNTs to obtain the accurate energy change. For example, the number of C and H atoms in junction of (10, 1)/(11, 0) is 176 and 22, respectively, and the number of total C and H atoms of two correspondingly separated tubes (10, 1) and (11, 0) is 88 and 11, respectively.

Fig. 1 Schematic cluster models of tube junctions showing the tube chirality changed from (a) (10, 1) to (11, 0), (b) (10, 1)to (9, 2), (c) (7, 5) to (8, 4), and (d) (7, 5) to (6, 6). The open-ends of all junctions are terminated by H atoms. The C and H atoms are represented by purple and blue balls, respectively. Those C atoms at the 5,7-defect sites are highlighted in green.

Fig. 2 presents a plot of the calculated energy needed (ΔE) to change chirality from (n, m) to (n±1, m∓1) for different SWCNTs as a function of the inverse of tube diameter. As we can see, the chirality change from (n, m) to (n±1, m∓1) for different SWCNTs is an endothermal process due to an indispensable 5,7-defect introduced in this case. Clearly, the calculatedΔE for different SWCNTs due to the chirality change from (n, m) to (n±1, m∓1) increases linearly with increasing the tube diameter, ranging from 1.1 eV for (5, 1) tube to 6.3 eV for an infinite large tube (graphene). This value (6.3 eV) of the formation energy of a single 5,7-defect in graphene is comparable to that in the previous work (7.5 eV)[37]. In order to better understand the nearly linear relationship between energies and tube diameters, we fit all the data plotted in Fig. 2 and obtained a linear relationship asE=-19.7/d+5.4. This is reasonable considering the fact that a small SWCNT has a larger curvature than the large ones, resulting in a larger formation energy and lower stability[9], thus it is more energetically feasible to introduce a 5,7-defect in small SWCNTs. Moreover, it is found that the energies needed to change the chirality of nAC tubes from (n, m) to (n±1, m∓1) are about 0.2- 0.4 eV larger than those of nZZ ones with comparable diameters (Fig. 2), implying that it is more energetically difficult to change the chirality from (n, m) to (n±1, m∓1) for nAC than nZZ tubes. It seems hard to understand why different tubes with the same diameter show different difficulties in changing their chiralities from (n, m) to (n±1, m∓1). Specifically, why a nZZ tube needs less energy to change its chirality than a nAC tube with almost the same diameter during the epitaxial growth, considering that only one 5,7-defect is introduced and the tube diameter does not change too much in this case.

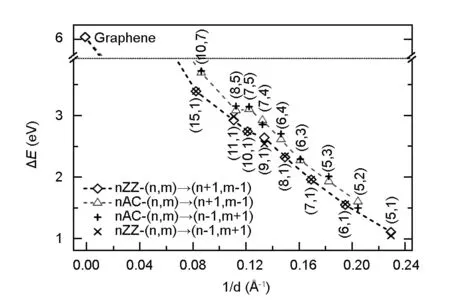
Fig. 2 The calculated energy change (ΔE in eV) of different SWCNTs due to the chirality change from (n, m) to (n±1, m∓1)as a function of the inverse of tube diameter. Open triangle (square)and plus sign (cross) symbols indicate the change of tube chirality from (n, m) to (n+1, m-1) and (n-1, m+1), respectively.The data of ΔE (the formation energy of a 5, 7-defect) for graphene is also included in this figure to represent the SWCNT with an infinite diameter.

For example, the diameter of (10, 1) tube changes from 8.3 to 8.6 and 8.0 Å after its chirality is changed to (11, 0) and (9, 2), respectively, and the (7, 5) tube changes its diameter from 8.2 to 8.3 and 8.1 Å after its chirality is changed to (8, 4) and (6, 6), respectively. However, as we can see from the atomic structures of tube junctions shown in Fig. 3a-d, the 5,7-defects show different orientations with the tube axis for different junctions, resulting in different intersection angles (θ) between the defect orientation and the tube axis. For example, the intersection angles for (9, 1) /(10, 0), (9, 1)/(8, 2), (7, 4)/(8, 3), and (7, 4)/(6, 5) junctions are 66°, 61°, 83°, and 79°, respectively. Fig. 3e shows the intersection angles (θ) of all (n, m) /(n±1, m∓1) tube junctions involved in this work as a function of the inverse of tube diameter. Interestingly, it is found that the intersection angles of different (n, m)/(n±1, m∓1) tube junctions for the nAC tubes are about 10°- 20° larger than those for the nZZ tubes. Therefore, more energies needed to change the chirality for nAC tubes than those for nZZ tubes (Fig. 2) can be ascribed to the largerθfor nAC tubes. Actually, it was reported that the larger intersection angle between the 5,7-defect and tube axis results in higher formation energies of the 5,7-defects in SWCNTs[40].

Fig. 3 The fully relaxed atomic structures of four tube junctions showing the tube chirality change from (a) (9, 1) to (10, 0), (b) (9, 1)to (8, 2), (c) (7, 4) to (8, 3), and (d) (7, 4) to (6, 5), the intersection angles (θ) between the orientation of 5, 7-defect and the tube axis are highlighted by red dashed lines. (e) The plot of intersection angles of all (n, m) /(n±1, m∓1) tube junctions for nZZ (nAC) tubes as function of the inverse of tube diameter.

In addition to the cases of chirality change from (n, m) to (n±1, m∓1) as discussed above, the chirality-changed epitaxial growth of SWCNTs with other chirality changes might occur if the energy inputs are large enough by severely altering the epitaxial growth condition. For the case of chirality change from (n, m) to (n±2, m∓2), in which the diameter change of a (n, m) tube is larger than that in the case of chirality change from (n, m) to (n±1, m∓1) and in consequence a larger energy is expected. In order to check this, we further calculate the energies needed to change the chirality from (n, m) to (n±2, m∓2) for different SWCNTs. As reported in ref. 32 that at least two 5,7-defects have to be introduced into a SWCNT to change its chirality from (n, m) to (n±2, m∓2). Following this speculation, we constructed the corresponding SWCNT junctions with the tube chirality change from (n, m) to (n±2, m∓2) for different SWCNTs. Fig. 4 shows fully relaxed atomic structures of four SWCNT tube junctions showing the chirality change from (7, 3) to (9, 1). Obviouly, two 5,7-defects introduced to change tube chirality from (n, m) to (n±2, m∓2) can be separated by different numbers of 6-member ring. As we can see in Fig. 4, the required energy for chirality change in this case increases with increasing the number of 6-member ring between two 5,7-defects. Thus, the tube junction with two adjacent 5,7-defects is the one that is most energetically stable. Actually, it was reported that the formation energy of a pair of 5,7-defects in SWCNTs increases with increasing the spacing distance between two 5,7-defects[41]，well consistent with our theoretical results. Therefore, tube junctions with two adjacent 5,7-defects were used to study the energy changes of different SWCNTs with the chirality changed from (n, m) to (n±2, m∓2) in this work.

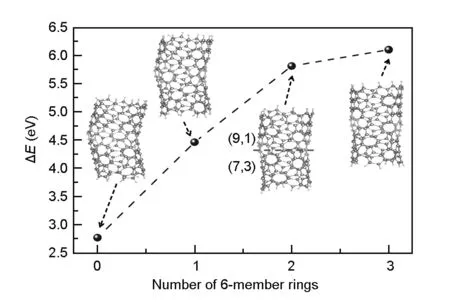
Fig. 4 The energy needed to change a (7, 3) to a (9, 1) tube as a function of the number of 6-member rings between two 5, 7-defects.The fully relaxed atomic structures of different junctions with different numbers of 6-member rings between two 5, 7-defects are also presented. The open-ends of all junctions are terminated by H atoms. The C and H atoms are represented by purple and blue balls, respectively. The C atoms at the 5, 7-defect sites are highlighted in green.

Similar to the case of chirality change from (n, m) to (n±1, m∓1), the chirality change of SWCNTs from (n, m) to (n±2, m∓2) are also found to be an endothermal process and the calculated energy changes of different SWCNTs considered in this work decrease linearly with decreasing the tube diameters (Fig. 5), ranging from 2.07 to 4.4 eV for tubes with diameters ranging from 5.7 to 10.5 Å. This linear relainship between the energy changes and tube diameters shown in Fig. 5 can be further described by an analytic linear equation as, Energy=-66.42/d+12.01. Interestingly, it is found that the required energies for chirality change of different SWCNTs from (n, m) to (n±2, m∓2) are less than two times of those for SWCNTs with a similar diameter from (n, m) to (n±1, m∓1). Considering that one 5,7-defect and two 5,7-defects are indispensably introduced to change the chirality of different SWCNTs from (n, m) to (n±1, m∓1) and from (n, m) to (n±2, m∓2), respectively, it seems that energy requirement for the former case should be about two times of that for the latter. However, it should be noted that two isolated 5,7-defects cause a larger lattice strain in SWCNTs than two adjacent 5,7-defects do. In fact, we found that the total energy of tube junction with two adjacent 5,7-defects is remarkably lower than that with two isolated ones for the same tube junction. For example, the total energy of the tube junction of (7, 3)/(9, 1) with two 5,7-defects separated by three 6-member rings was calculated to be 3.3 eV higher than that of the most stable one with two adjacent 5,7-defects (Fig. 4).

Fig. 5 The calculated energy changes (ΔE in eV) of different SWCNTs due to the chirality change from (n, m) to (n±2, m∓2)as a function of the inverse of tube diameter. The data of ΔE(the formation energy of a pair of neighboring 5, 7-defects)for graphene is also shown to represent the SWCNT with an infinite diameter.

4 Conclusions

In contrast to the chirality-unchanged epitaxial growth, the energy required is found to be several electron volts for the chirality-changed epitaxial growth of SWCNTs based on the DFT calculations. The energy needed for a chirality change of different SWCNTs decreases linearly with decreasing tube diameter. More energy is required for the nAC tubes to change the chirality from (n, m) to (n±1, m∓1) than those for the nZZ tubes with the comparable diameters, due to a larger formation energy for 5,7-defects introduced in the nAC tubes. It is also found that the energy requirement to change the tube chirality from (n, m) to (n±2, m∓2) is less than two times of those in the case of chirality change from (n, m) to (n±1, m∓1) for SWCNTs with the comparable diameters, due to a less strain induced by two adjacent 5,7-defects than that by two isolated 5,7-defects. We believe that our DFT results may provide a better understanding on the chirality changed epitaxial growth of SWCNTs and guide the synthesis of single-chirality SWCNTs by an epitaxial growth in the future.

Acknowledgements

We acknowledge the support from Shenyang Supercomputing Center (CAS). Part of this work was carried out at National Supercomputer Center in Tianjin, and the calculations were performed on TianHe-1(A). We also acknowledge Dr. Bi-Lu Liu of University of Southern California for fruitful discussions.

[1] Jorio A, Dresselhaus G, Dresselhaus M S. Carbon Nanotubes : Synthesis, Structure, Properties, and Applications[M]. Springer, Berlin, New York, 2001.

[2] Saito R, Fujita M, Dresselhaus G, et al. Electronic structure of chiral graphene tubules[J]. Appl Phys Lett, 1992, 60(18): 2204-2206.

[3] Tans S J, Verschueren A R M, Dekker C. Room-temperature transistor based on a single carbon nanotube[J]. Nature, 1998, 393(6680): 49-52.

[4] Shulaker M M, Hills G, Patil N, et al. Carbon nanotube computer[J]. Nature, 2013, 501(7468): 526-530.

[5] Wu Z C, Chen Z H, Du X, et al. Transparent, conductive carbon nanotube films[J]. Science, 2004, 305(5688): 1273-1276.

[6] Deheer W A, Chatelain A, Ugarte D. A carbon nanotube field-emission electron source[J]. Science, 1995, 270(5239): 1179-1180.

[7] Kreupl F, Graham A P, Duesberg G S, et al. Carbon nanotubes in interconnect applications[J]. Microelectron Eng, 2002, 64(1-4): 399-408.

[8] Cambre S, Wenseleers W, Goovaerts E, et al. Determination of the metallic/semiconducting ratio in bulk single-wall carbon nanotube samples by cobalt porphyrin probe electron paramagnetic resonance spectroscopy[J]. ACS Nano, 2010, 4(11): 6717-6724.

[9] Kato K, SaitoS, Geometries. electronic structures and energetics of small-diameter single-walled carbon nanotubes[J]. Physica E, 2011, 43(3): 669-672.

[10] Wang H, Yuan Y, Wei L, et al. Catalysts for chirality selective synthesis of single-walled carbon nanotubes[J]. Carbon, 2015, 81: 1-19.

[11] Loebick C Z, Podila R, Reppert J, et al. Selective synthesis of subnanometer diameter semiconducting single-walled carbon nanotubes[J]. J Am Chem Soc, 2010, 132(32): 11125-11131.

[12] Li X L, Tu X M, Zaric S, et al. Selective synthesis combined with chemical separation of single-walled carbon nanotubes for chirality selection[J]. J Am Chem Soc, 2007, 129(51): 15770-15771.

[13] He M S, Jiang H, Liu B L, et al. Chiral-selective growth of single-walled carbon nanotubes on lattice-mismatched epitaxial cobalt nanoparticles[J]. Sci Rep, 2013, 3: 1460(1)-1460(7).

[14] Wang H, Wei L, Ren F, et al. Chiral-selective CoSO4/SiO2Catalyst for (9,8) single-walled carbon nanotube growth[J]. Acs Nano, 2013, 7(1): 614-626.

[15] Dutta D, Chiang W H, Sankaran R M, et al. Epitaxial nucleation model for chiral-selective growth of single-walled carbon nanotubes on bimetallic catalyst surfaces[J]. Carbon, 2012, 50(10): 3766-3773.

[16] Fouquet M, Bayer B C, Esconjauregui S, et al. Highly chiral-selective growth of single-walled carbon nanotubes with a simple monometallic Co catalyst[J]. Phys Rev B, 2012, 85: 235411(1)-235411(7).

[17] Liu B L, Ren W C, Li S S, et al. High temperature selective growth of single-walled carbon nanotubes with a narrow chirality distribution from a CoPt bimetallic catalyst[J]. Chem Commu, 2012, 48(18): 2409-2411.

[18] He M, Chernov A I, Fedotov P V, et al. Predominant (6,5) single-walled carbon nanotube growth on a copper-promoted iron catalyst[J]. J Am Chem Soc, 2010, 132(40): 13994-13996.

[19] Wei L, Wang B, Goh T H, et al. Selective enrichment of (6,5) and (8,3) single-walled carbon nanotubes via cosurfactant extraction from narrow (n,m) distribution samples[J]. J Phys Chem B, 2008, 112(10): 2771-2774.

[20] Wang H, Wang B, Quek X Y, et al. Selective synthesis of (9, 8) single-walled carbon nanotubes on cobalt incorporated TUD-1 catalysts[J]. J Am Chem Soc, 2010, 132(47): 16747-16749.

[21] Chiang W H, SankaranR M. Linking catalyst composition to chirality distributions of as-grown single-walled carbon nanotubes by tuning NixFe1-x nanoparticles[J]. Nat Mater, 2009, 8(11): 882-886.

[22] Yang F, Wang X, Zhang D Q, et al. Chirality-specific growth of single-walled carbon nanotubes on solid alloy catalysts[J]. Nature, 2014, 510(7506): 522-524.

[23] Sanchez-Valencia J R, Dienel T, Groning O, et al. Controlled synthesis of single-chirality carbon nanotubes[J]. Nature, 2014, 512(7512): 61-64.

[24] Lei Z X, Liu J, Wang J B, et al. The effects of catalyst structure and morphology on the growth of carbon nanotubes[J]. New Carbon Materials, 2003, 18(4): 271-276.

[25] Song J L, Wang L, Feng S A, et al. Growth of carbon nanotubes by the catalytic decomposition of methane over Fe-Mo/Al2O3catalyst: Effect of temperature on tube structure[J]. New Carbon Materials, 2009, 24(4): 307-313.

[26] Yao Y G, Feng C Q, Zhang J, et al. “Cloning” of single-walled carbon nanotubes via open-end growth mechanism[J]. Nano Lett, 2009, 9(4): 1673-1677.

[27] Liu J, Wang C, Tu X M, et al. Chirality-controlled synthesis of single-wall carbon nanotubes using vapour-phase epitaxy[J]. Nat Commun, 2012, 3: 1199(1)-1199(7).

[28] Yao Y G, Li Q W, Zhang J, et al. Temperature-mediated growth of single-walled carbon-nanotube intramolecular junctions[J]. Nat Mater, 2007, 6(4): 283-286.

[29] Kresse G, Furthmuller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Phys Rev B, 1996, 54(16): 11169-11186.

[30] Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J]. Phys Rev Lett, 1996, 77(18): 3865-3868.

[31] Blochl P E. Projector augmented-wave method[J]. Phys Rev B, 1994, 50(24): 17953-17979.

[32] Kresse G, Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method[J]. Phys Rev B, 1999, 59(3): 1758-1775.

[33] Saito R, Dresselhaus G, Dresselhaus M S. Physical Properties of Carbon Nanotubes [M]. Imperial College Press, London, 1996.

[34] Chico L, Crespi V H, Benedict L X, et al. Pure carbon nanoscale devices: Nanotube heterojunctions[J]. Phys Rev Lett, 1996, 76(6): 971-974.

[35] Ouyang M, Huang J L, Cheung C L, et al. Atomically resolved single-walled carbon nanotube intramolecular junctions[J]. Science, 2001, 291(5501): 97-100.

[36] Wei D C, LiuY Q. The intramolecular junctions of carbon nanotubes[J]. Adv Mater, 2008, 20(15): 2815-2841.

[37] Yazyev O V, LouieS G. Topological defects in graphene: Dislocations and grain boundaries[J]. Phys Rev B, 2010, 81: 195420(1)-195420(7).

[38] Grantab R, Shenoy V B, Ruoff R S. Anomalous strength characteristics of tilt grain boundaries in graphene[J]. Science, 2010, 330(6006): 946-948.

[39] Huang P Y, Ruiz-Vargas C S, van der Zande A M, et al. Grains and grain boundaries in single-layer graphene atomic patchwork quilts[J]. Nature, 2011, 469(7330): 389-392.

[40] Zhou L G, Shi S Q. Formation energy of stone-wales defects in carbon nanotubes[J]. Appl Phys Lett, 2003, 83(6): 1222-1224.

[41] Yuan Q H, Xu Z P, Yakobson B I, et al. Efficient defect healing in catalytic carbon nanotube growth[J]. Phys Rev Lett, 2012, 108: 245505(1)-245505(5).

Changing the chirality of single-wall carbon nanotubes during epitaxial growth: A density functional theory study

SHEN Wei, LI Feng, LIU Chang, YIN Li-chang

(ShenyangNationalLaboratoryforMaterialsScience,InstituteofMetalResearch,ChineseAcademyofSciences,Shenyang110016,China)

The energetic of the change in the chirality of single-wall carbon nanotubes (SWCNTs)during epitaxial growth from (n, m) to (n±Δ, mΔ)(Δ=1, 2) was investigated by density functional theory calculations. The calculated energies for changing the chirality of different SWCNTs show a nearly linear decrease with decreasing tube diameter. In the case ofΔ=1, more energy input is needed for near armchair (nAC) SWCNTs to change their chiralities than those for near zigzag (nZZ) SWCNTs with comparable diameters, due to the larger formation energies of pentagon-heptagon defects (5,7-defects) introduced in the nAC-SWCNTs. These larger formation energies for the nAC-SWCNTs come from the larger angles between the orientation of a 5,7-defect and the tube axis than those for nZZ-SWCNTs. The topological connection oftwo adjacent 5,7-defects, which is indispensable for changing the chirality during growth in the case ofΔ=2, is found to be energetically most stable. The energies needed to change chirality in the case ofΔ=2 are calculated to be less than twice those in the case ofΔ=1 for SWCNTs with comparable diameters. These results may help us understand the change in chirality during the epitaxial growth of SWCNTs and guide the future synthesis of SWCNTs with a single-chirality .

Single-walled carbon nanotube; Chirality-changed; Pentagon-heptagon defect; Epitaxial growth; Density functional theory

National Natural Science Foundation of China (51272257, 51202255, 51472249).

YIN Li-chang, Associate Professor. E-mail: lcyin@imr.ac.cn

国家自然科学基金项目(51272257, 51202255, 51472249).

尹利长，副研究员. E-mail: lcyin@imr.ac.cn

作者介绍：谌 为，博士研究生. E-mail: weichen@imr.ac.cn

1007-8827(2016)05-0525-07

TQ127.1+1

A

Authorintroduction: SHEN Wei, Ph. D Candidate. E-mail: weichen@imr.ac.cn

10.1016/S1872-5805(16)60030-6

Receiveddate: 2016-07-29；Reviseddate: 2016-10-03

English edition available online ScienceDirect (http:www.sciencedirect.comsciencejournal18725805).