基于BP神经网络的光伏电站辐照度预测研究

2016-11-22衢州职业技术学院信息工程学院廖东进刘晓龙

太阳能 2016年10期

衢州职业技术学院信息工程学院 ■ 廖东进刘晓龙

衢州职业技术学院信息工程学院 ■ 廖东进*刘晓龙

由于现有神经网络辐照度预测模型的输入变量多为辐照度的历史数据问题,为了更准确衡量辐照度的变换关系，引入其他与辐照度相关因子作为模型输入变量，提高模型预测性能；其次，根据同期同日类型的辐照度变化关联性，对辐照度预测模型提出了由辐照度预测值和辐照度均值组成的加权修正方法，辐照度预测值权重为N天实际与理论曝辐量比值的均值，辐照度均值权重为日类型修正系数和当天实际与理论曝辐量比值的乘积；最后归一化权重，构建了基于日类型的神经网络辐照度预测模型。采用本地历史数据进行仿真，结果验证了改进输入模型的合理性和输出模型的有效性。

光伏电站；辐照度；功率预测；神经网络

0　引言

截至2014年底，我国光伏电站累计安装量超28 GW，增长速度超60%。2014年光伏发电量约250亿kWh，同比增长超过200%[1]。随着我国光伏电站规模不断扩大推广，提高光伏电站辐照度预测精度将有利于功率预测及电网安全调度与电网运行。

直接预测法和分步预测法是当前光伏电站功率预测的两种主要模式[2]。直接预测法就是以历史发电功率、气象数据、天气预报等信息作为预测模型输入，输出为未来24～72 h的电站功率预测值。分步预测法就是将功率预测分为辐照度预测和电站物理特性建模两步。由于当前光伏电站建设种类较多，规模较大，直接预测法存在较多不确定因素，预测精度存在较大误差而分步预测法可与光伏发电各影响因素很好地结合，其功率预测效果更加可靠。

1　辐照度预测研究现状

由于神经网络算法具有自适应学习、大数据处理等特点，在辐照度预测等方面得到了较好的应用；文献[3]以日辐照度均值、温度均值和积日为模型输入，利用多层感知器建立了提前1天的预测模型；文献[4]以历史云量、预报信息作为模型输入，采用小波神经网络模型，建立预测模型；文献[5]以辐射曝辐量为模型输入，建立了小波神经网络预测模型；文献[6]以各类气象参数、地理信息等参数为模型输入，建立太阳逐时辐射量预测模型；文献[7]以历史气象数据、气象状态为模型输入，建立了相似日辐照度预测模型。

研究表明，采用神经网络算法和其他算法相结合能取得较好的辐照度预测效果，但在神经网络模型输入及输出修正方面还有待改进。主要表现为：1)仅利用同期同日类型的历史辐照度数据作为模型输入，不能全面描述该日类型的辐照度变换规律，输入模型的参数选择和特征提取有待改进；2)辐照度预测值和同期同日类型辐照度具有一定影响性和相似性，对模型输出存在较大影响。

为了实现辐照度预测，本文采用自适应学习机理的BP神经网络算法，并在预测模型的输入及输出修正上进行了改进。首先，分析模型输入变量的选择、特征提取对模型输出预测误差指标的影响；其次，针对日类型对辐照度变化的影响性和相似性特性，提出模型预测值的加权修正方法。

2　研究对象

本文实际测量和验证数据测试点为衢州职业技术学院100 kW分布式光伏电站，地理坐标为东经118°01′，北纬28°14′，光伏电站位于楼顶。图1、图2为实测地理信息和设备情况。

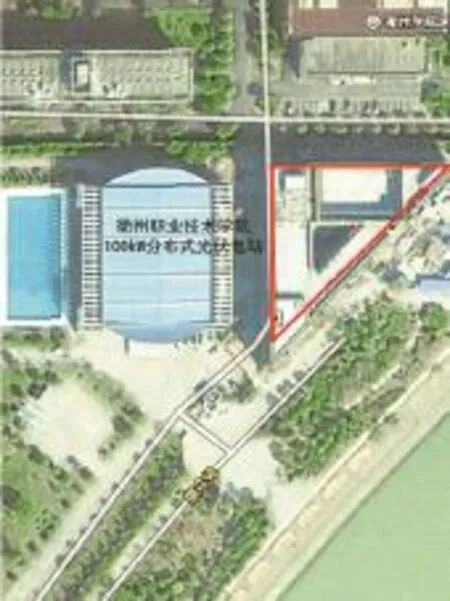
图1　实测地理信息

图2　气象测量设备

气象参数测量设备型号为锦州阳光PC-4-A，可测量当地环境温度、湿度、露点温度、风速、辐射、日照时数等气象参数，测量精度为0.5 h。

3　基于历史辐照度数据的神经网络模型构建

3.1神经网络模型

神经网络分为反馈网络(Feedback NNs)、前向网络(Feedforward NNs)、自组织网络(Selforganizing NNs) 3大类。其中，一种按误差逆传播算法训练的BP(Back Propagation)神经网络在辐照度预测领域中效果较好[8]。

BP神经网络模型由输入层、隐含层和输出层构成，根据辐照度预测模型，其学习过程为辐照度样本信号的正向学习过程和辐照度误差的反向学习过程。

首先，将辐照度样本送入输入层，经过隐含层学习处理后，送往输出层；将输出值和预期结果进行比较，如果不符合，将进入辐照度误差的反向学习过程，分摊给各层所有单元，修正各单元权值，产生新的模型输出，如果误差不符，继续反向循环，直到误差满足期望值要求。其模型结构及学习过程如图3所示。

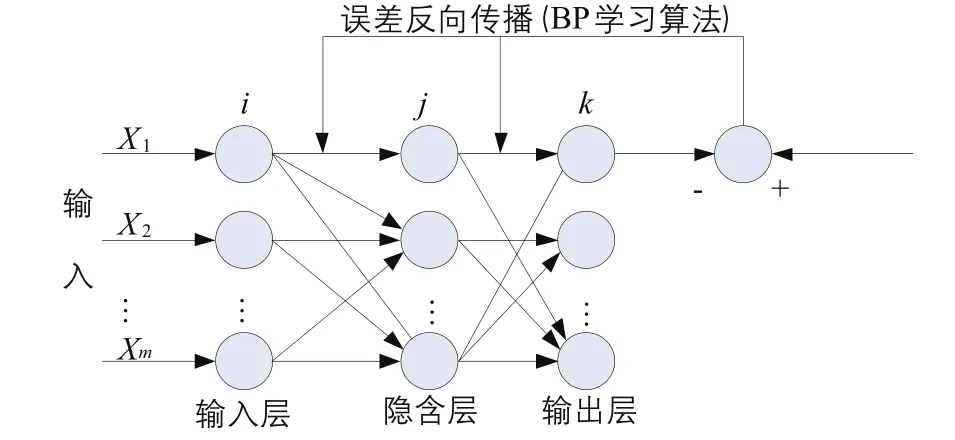
图3　BP神经网络的一般结构

3.2模型输入参数

为了保证BP神经网络模型数据挖掘能力和预测精度，输入模型参数不宜过多也不宜过少，过多会影响模型数据挖据，过少会影响模型预测精度。基于历史辐照度数据的BP神经网络模型输入为太阳辐照度历史数据gs,j。本文考虑一天24 h中，18:00～次日06:00，辐射接近零，且光伏电站基本不发电，故预测数据的输入和输出为06:00～18:00，精度0.5 h，历史辐照度数据量为24个(06:00和18:00合一个数据)。

3.3日类型分类

为了BP神经网络模型的有效学习，保证辐照度预测的准确性，将一年的日类型划分为4类。具体划分内容如表1所示。

表1　日类型对照表

3.4隐含层及输出层结构设计

基于历史辐照度数据的神经网络模型釆用前一个同日类型的24个历史辐照度作为输入，输入层神经元数目依据输入维数和输出而定。

在神经网络隐含层层数设计上，为了获取任意非线性映射关系，单隐含层的神经元数目要求较多，但其计算效率会随神经元数量的增加而急剧下降，故层数设计为两层。

双隐含层的神经元数量设定初步可由输入样本数目和上述单隐层的经验公式确定，然后通过交叉验证的方法[9]，以获取最小平均绝对偏差MABE和均方根误差RMSE为目标，来确定隐含层个数和隐含层神经元数。其中，RMSE和MABE如式(1)、(2)所示[10]：

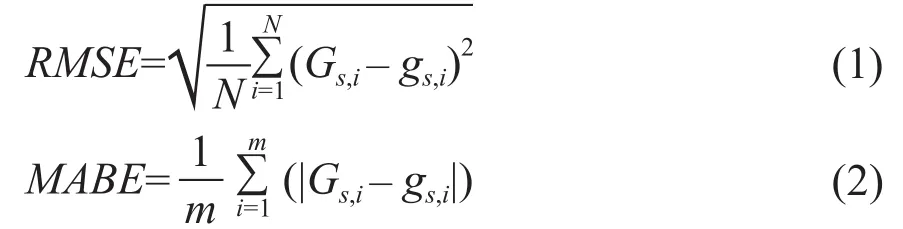
式中，Gs,i为辐照度预测值；gs,i为辐照度实测值，i为采样点，表示时间，i=1,…, m，其中m为06:00～08:00采样点个数，m=24；s为积日，即日期在年内的序号，如1月1日积日，s为1，1月7日积日，s为7，闰年最大积日值为366。

4　输入模型结构优化

基于历史数据的神经网络模型预测系统中，输入值为预测前1天或2天的历史辐照度数据。由于影响辐照度的因素还有如大气层散射、反射，大气质量，温度，湿度等其他气象要素，仅用一种历史辐照度数据参数很难准确表示同日类型辐照度变化规律，所以在模型输入参数选择上引入了辐照度均值、辐照度方差、温度均值、积日等气象参数。

为了验证输入模型参数选择、特征量提取对模型输出误差指标的影响，本文建立了两种输入模型结构。模型1为输入数据为历史辐照度gs,i，模型2的输入数据为辐照度均值gjz、辐照度方差gf、积日s、温度均值Tt等4维数据。

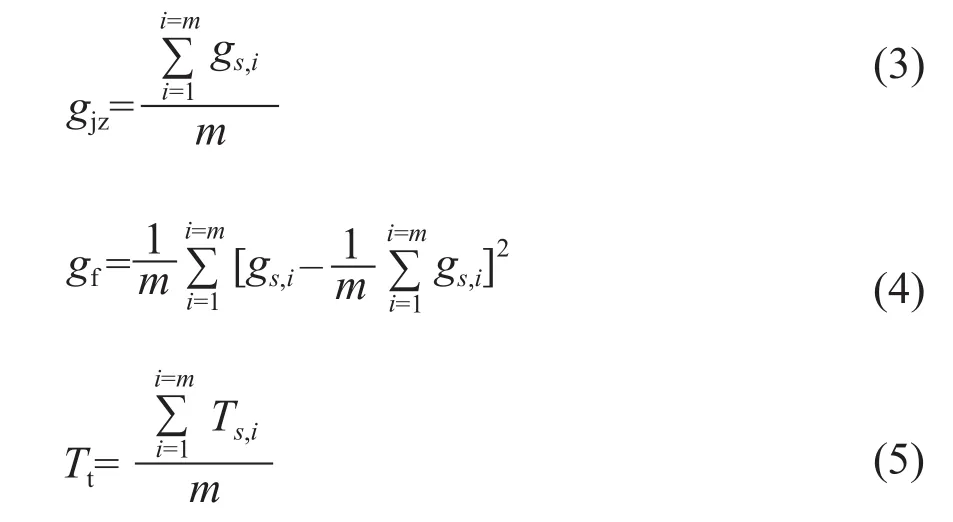
式中，Ts,i为i采样点(时刻)的温度。

5　基于日类型差异的模型输出修正

5.1日类型与辐照度关系

在一年中，随着地球公转和自转运动，地表外的辐照度呈现周期性的变化规律；而地表辐照度由于受大气层云量、散射、反射等因素影响,呈现不同的变化特点。如在晴天、阴天时，地表辐射的变化规律类似地表外辐照度变化规律；而在降水量日类型下，地表辐照度变化和地表外辐照度变化存在较大差异。

地表外理论辐照度计算方法如下：

式中，K为日地距离修正系数；G0为太阳能常数，取1368 W/m2；δ为太阳赤纬角；φ为当地经度；ω为太阳时角。当已知地点、日期、时间时，就可以求出理论辐射量。图4为同期4类日类型实测辐照度和理论辐照度的对应曲线图。

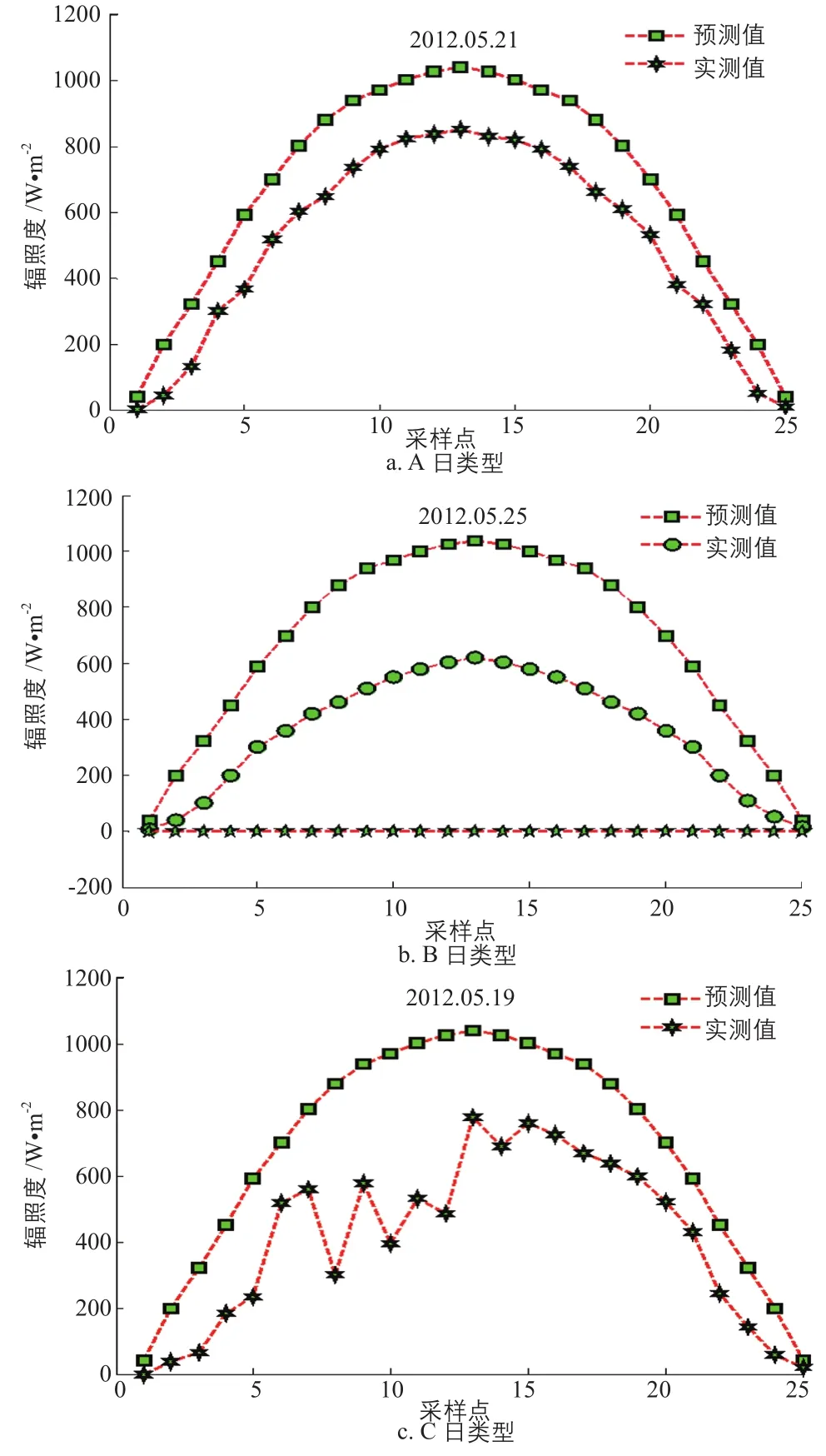
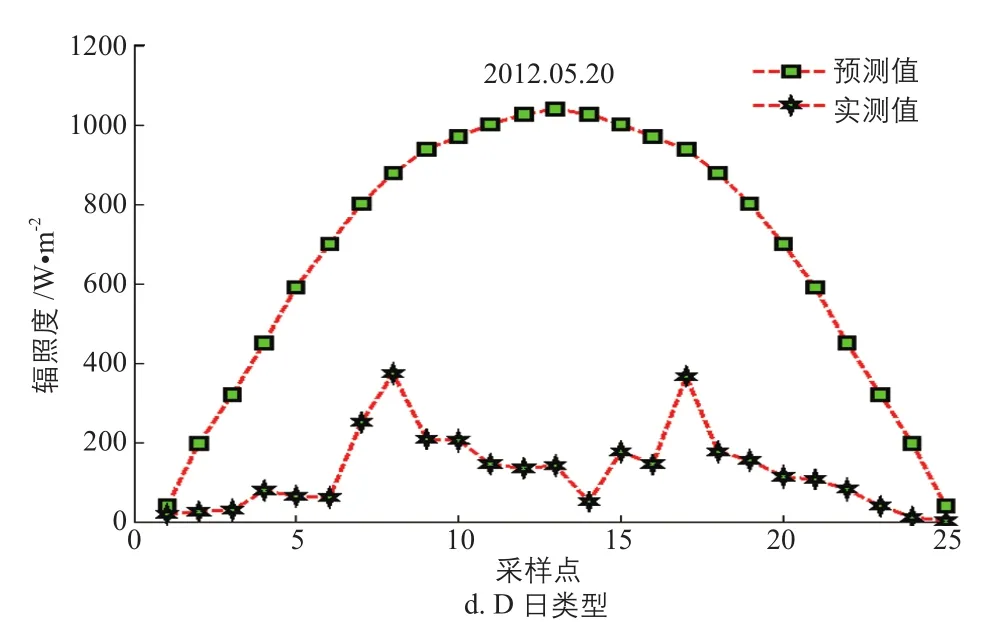
图4　4类日类型辐照度曲线

从图4可看出，A、B日类型两种天气较好的地表辐照度与地表外辐照度的关联性较强，其变化规律具有一定的相似性，所以利用这种同期同日类型在辐照度变化规律的相似性，引入日类型修正系数，可对预测模型输出进行修正。另外，对于同期同日类型某时刻辐照度值也存在一定的关联性，如在同期7月的低降水量C日类型中，第7个采样点(09:00)辐照度约为550 W/m2，可以提取历史同期同日类型的辐照度均值对输出模型进行修正。

5.2日类型输出修正方法

引入同期同日类型和辐照度变化关系，辐照度预测模型值修正方法为：辐照度预测值和历史同期同日类型的辐照度均值进行联合加权。为了衡量日类型对各项权重指标的影响，引入曝辐量参数和日类型修正系数。辐照度预测值权重取N天实际与理论曝辐量比值的均值，N=3；辐照度均值权重取日类型修正系数和当天的实际与理论曝辐量的比值的乘积。最后，归一化预测值权重和均值权重，得到基于日类型修正方法的辐照度预测模型。

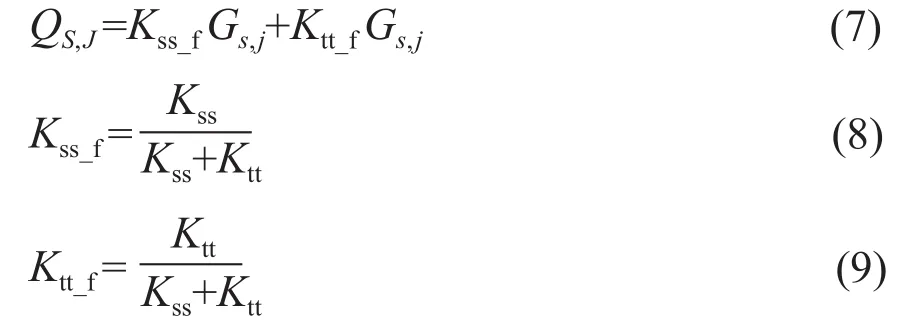
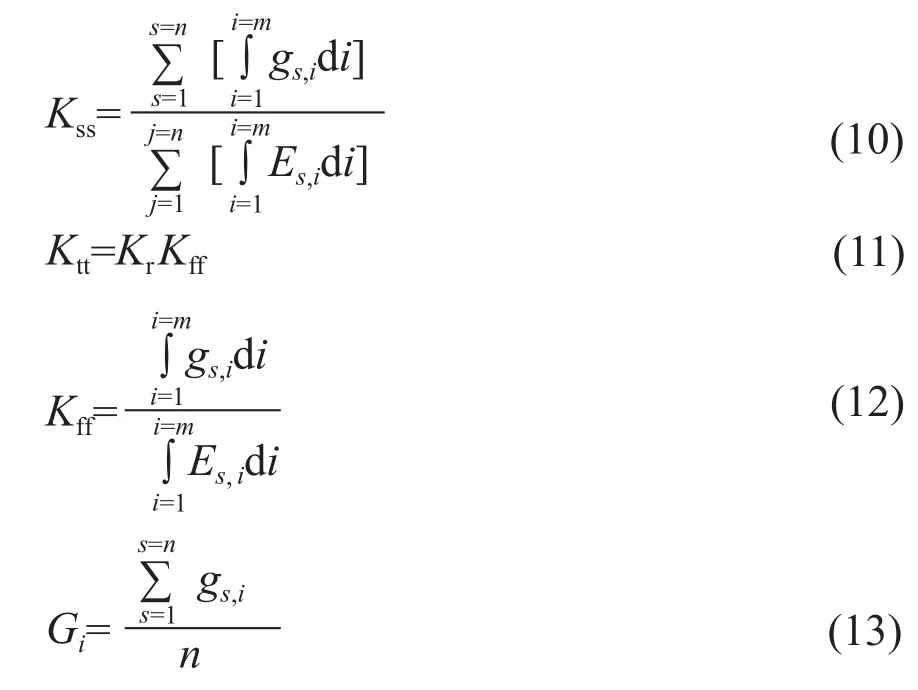
式中，QS,J为辐照度修正后预测值；Gs,j为辐照度预测值；Kss_f为归一化的模型预测值的修正权重；Ktt_f为归一化的同期辐照度的修正权重；Ktt为辐照度均值权重；Kss为预测值的修正权重；Kff为实际与理论曝辐量的比值；Gi为同日类型历史同时期的辐照度均值；Kr为日类型修正系数，针对4种不同天气类型分别取1、0.6、0.2、0；n为天数，取3；m为一天中采样点数，取24。

6　神经网络模型预测仿真分析

综上分析，本文构建了两种不同输入模型的基于日类型修正方法的BP神经网络辐照度预测模型，图5为其流程图。

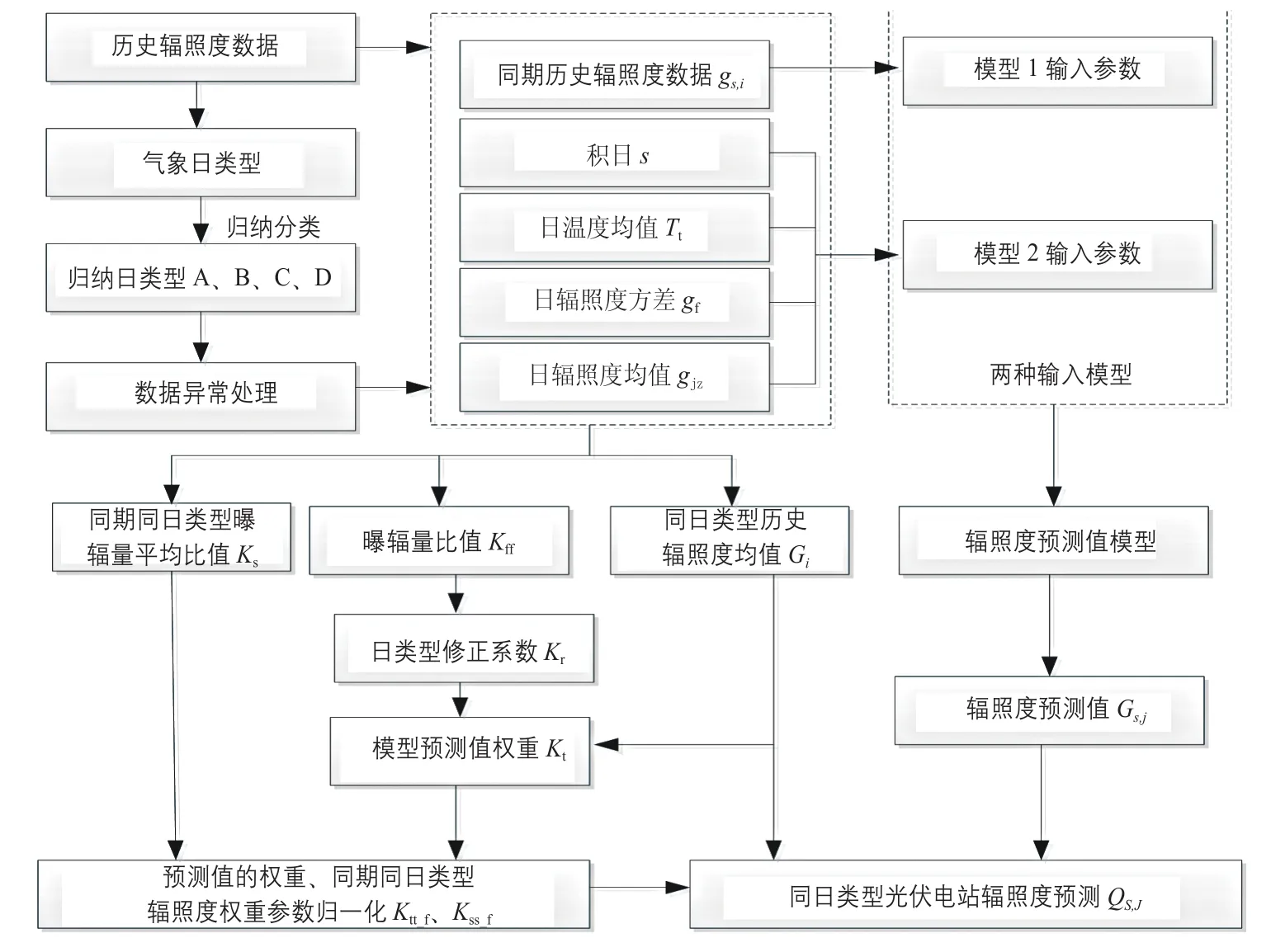
图5　辐照度预测修正方法流程图

针对上述4种日类型，A、B类辐照度变化较平稳，C、D类辐照度变化较剧烈。图6给出了B、D两种典型日类型预测辐照度、误差曲线图。表2给出了B、D两种日类型在输入模式1和输入模式2无预测输出修正情况下的误差指标，同时也给出了在输入模式2有预测输出修正情况下的误差指标。

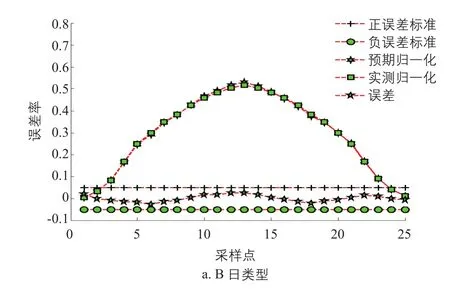
图6　辐照度预测误差

对比输出无改进的预测模型，在预测模型输入模型中引入温度均值、辐照度均值、辐照度方差、积日等与辐照度直接相关的因子之后，在D日类型下，MABE从原0.08451降低到0.07905，R2从0.6852提升到0.8540；同时，采用输入模型2时，采用预测输出改进方法，在D日类型下，MABE从原0.07905降低到0.07714，R2从0.8540提升到0.8806。从上述结果来看，采用基于日类型修正方法的BP神经网络辐照度预测模型提升了辐照度预测精度，能较好的提高不同日类型下的预测精度。

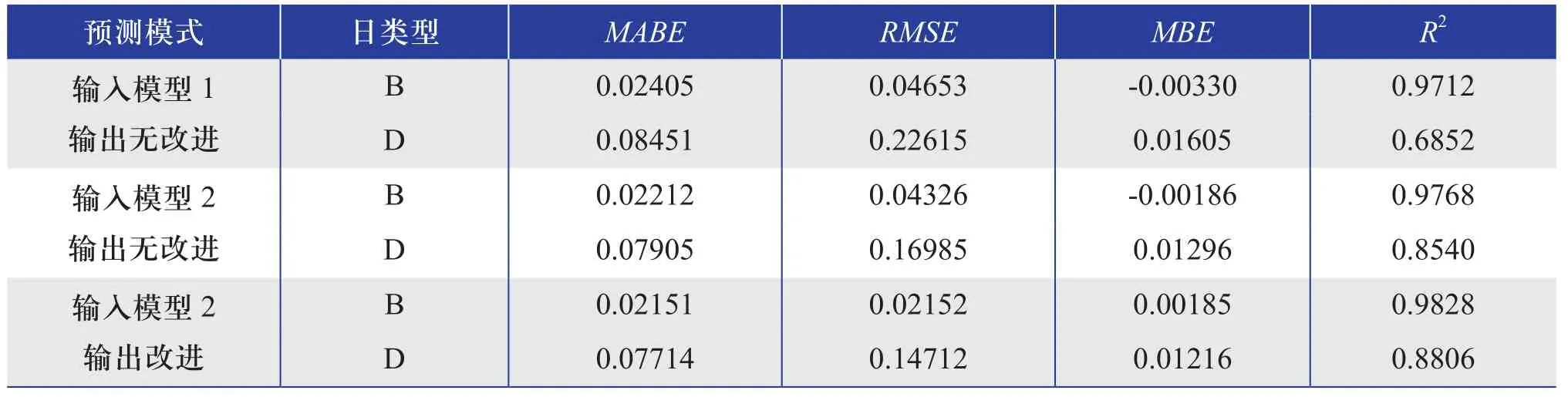
表2　预测模型的误差指标

7　结论

本文对现有基于历史辐照度为输入源的BP神经网络模型进行了分析，结合辐照度直接相关因素，引入温度均值、辐照度均值、辐照度方差、积日等特征参数，对神经网络输入模型进行了改进；同时结合日类型对辐照度预测的影响，提出基于日类型差异的模型输出修正方法。采用当地实际历史数据进行仿真，结果表明，改进后的预测模型在输出MABE、RMSE、MBE、R2等各项误差指标上得到了提升，预测精度得到了较好改善。由于辐照度与气象较多参数存在的关联，本文只对有限的气象参数进行了研究，因此神经网络输入模型参数选取还有待挖掘和改进；另外，在预测模型输出值的修正过程中，权重修正方式、修正系数的选取及优化是影响修正效果的重要因素，应此对预测值的修正方式还有待进一步研究。

[1] 中华人民共和国国家能源局. 国家能源局发布2014年光伏产业发展情况[EB/OL]. http://www.nea.gov.cn/2015-03/30/ c_134108941.htm. 2015-03.

[2] 王飞. 并网型光伏电站发电功率预测方法与系统[D]. 北京:华北电力大学电气与电子工程学院, 2013.

[3] 曹双华, 曹家枞. 太阳逐时总辐射混沌优化神经网络预测模型研究[J]. 太阳能学报, 2006, 27(2): 164－169.

[4] 王晓兰, 葛鹏江. 基于相似日和径向基函数神经网络的光伏阵列输出功率预测[J]. 电力自动化设备, 2013, 33(1): 100－103, 109.

[5] 焦李成. 神经网络系统理论[M]. 西安: 西安电子科技大学出版社, 1996.

[6] 王哲. 基于ANN和时间周期性的光伏电站辐照度预测研究[D]. 北京: 华北电力大学电气与电子工程学院, 2012.

[7] 张岚, 张艳霞, 郭嫦敏, 等. 基于神经网络的光伏系统发电功率预测[J]. 中国电力, 2010, 49(9): 75－78.

[8] 马金玉. 中国地面太阳辐射长期变化特征及短期预报方法研究[D]. 南京: 南京信息工程大学, 2013.

[9] 张佳伟. 光伏并网发电系统短期发电功率预测研究[D]. 南京: 南京信息工程大学, 2013.

[10] 米增强, 王飞, 杨光, 等. 光伏电站辐照度ANN预测及其两维变尺度修正方法[J]. 太阳能学报, 2013, 34(2): 251－258.

2016-04-19

衢州市科技计划项目(2014Y019)；2015年浙江省自然科学基金(Y15B020047)