岩层破裂微震信号小波分析中小波基的选取

王强，陈迅

（江苏科技大学 江苏 镇江 212003）

岩层破裂微震信号小波分析中小波基的选取

王强，陈迅

（江苏科技大学 江苏 镇江 212003）

传统的信号分析只能对完全的时域或完全的频域进行分析，而小波可以描述信号时间（空间）和频率（尺度）域的局部特性。小波变换是一种有效的处理微震信号的工具。然而，在分析同一信号时，不同的小波基会产生不同的结果。通过分析常用小波基的特点和岩层破裂微震信号的特点，结合计算的信噪比（SNR）和均方根误差（RMSE）的结果来选择合适的小波基。经过Sym 8降噪处理后的SNR和RMSE分别是30.4184和1.3109e-07；经过Coif 2降噪处理后的SNR和RMSE分别是35.2176和1.0312E-07。结果发现Sym 8和Coif 2适合用于分析岩层破裂微震信号。

小波分析；小波基；微震信号；信噪比；均方根误差

岩层是一种应力介质，当它变形破坏时，它的内部会因为破裂而扩展，同时将伴随着低能耗的声发射现象。当破裂程度达到约一半时，一系列的裂缝开始出现，并且会产生高能量声发射现象，通常被称为“脉动”。在某种程度上，微震和声发射现象的强度和频率反映了能量释放的速率[1]。微震监测最早开始于上世纪90年代，常用的分析微震信号的方法有对特征参数进行分析或者波形进行分析。特征参数分析法自1990年以上，被广泛应用于微震信号分析中。对矿山微震监测的历史延伸到大约只有20多年。它的优点在于能够记录大量的信息和更快的处理速度。然而这种处理方法也会丢失大量的原始波形信息。自1990年模态声发射理论的建立以来，波形分析方法，如模态分析和小波分析，已经在信号分析、图像压缩、地震检测等领域得到了越来越多的关注[2]。

许多小波基可用于信号的分析。然而对相同的信号进行分析时，不同的小波基会产生不同的结果[3]。为了能够对岩层破裂微震信号进行合理、准确的小波分析，岩层破裂微震信号将作为当前研究中的研究对象。微震信号经过降噪处理之后，有利于更精确的提取信号的各种特征，如相位、幅值、能量谱系数等。通过对这些特点的分析，可以进一步探测岩层破裂事件。

1　小波基

由于不同小波基的不同特征，我们需要了解常用小波基的主要特征以及它们的适用场合。选取一种恰当的小波基是非常重要的，它能够提高分析结果的精确度。这就需要我们对基本的小波基的特性有所了解，根据实际环境的需求，选出一个最恰当的小波基。

1.1小波基的性质

1）正交性：当小波变换的基函数是正交时，Mallat快速算法可以用于小波变换

2）对称性：对称小波基可以避免信号在分解和重构时的失真

3）紧支性：小波是紧支的。如果紧支宽度越窄，那么它的局部特性就越好

4）正则性：用于描述函数的光滑程度。

5）消失矩：信号能量集中在几个小波系数中，它监测信号的奇异性，并将信号从噪声中分离出来。

1.2几种常用的小波基函数

常用的小波基函数如表1所示。

表1　常见小波基及其特性

Haar小波：一般又称为哈尔小波，它是小波分析中被最早用到的正交小波基，同时也是最简单的。

Daubechies（dbN）小波：具有较好的正则性，使得信号的重构过程较为光滑，这是小波发展的一个里程碑，也使得分析离散小波成为了可能。Daubechies系列小波可以缩写成dbN，其中N=1，2，3，……，10。随着N的增大，能够增加局部特性、频带的划分效果，减弱时域的紧支性，大大增加了计算量，导致时实性严重降低[4]。由于它不具有对称性，所以在信号的小波分析和重构时会出现相位失真的现象，但是这并不对它的使用造成太大的影响，它应用范围依旧相当的广泛[5]。当N=1为特殊情况，即为Haar小波。

Symlet小波：是一种近似对称的小波函数，它是Daubechies的优化版，比Daubechies小波具有更好的对称性，能够从一定程度上降低在信号的小波分析和重构时产生的相位失真。Symlet系列小波可以表示为SymletN，其中N=2，3，…，8。

Morlet小波：是高斯包络下的单频率正弦函数，具有解析表达式，但没有紧支性和正交性[6]。Morlet小波是一个复值小波，通常被广泛应用于地震物理信号分析中，它能提取信号的幅值及其相位信息[7-8]。

2　岩层破裂微震信号的小波基

2.1小波基函数选取的原则

小波时频局部特性和小波变换的多尺度扩展了基于小波变换的信号处理技术应用的范围。不同的小波函数具有不同的时频特性。在实际选择恰当的小波基时，各种小波函基的特征及用途需要被重点考虑[9]。虽然许多学者都已经构建了许多的小波函数，但是只有几个小波函数可以有效地用于信号的处理，并且不是所有的小波函数都适用于微震信号的处理。在使用小波分析某个信号时，通常使用下面3种方法来选择小波基。

1）直接比较小波基的各种数学参数的。这种方法通常被用在从理论上分析如何选择合适的小波基。因为所有小波的数学参数完全是从数学的角度建立的，所以它具有一定的理论深度，但缺乏实践性，与工程实践结合的难度较高[10]。所以这种直接比较的方法，到目前为止还没出现一个系统的方法。

2）依据处理的信号选取几种合适的小波基，然后比较它们的处理效果。这种方法的优点是与工程实践结合，但是小波的选择性和应用过于片面。

3）依据传统信息价值函数，对小波基进行比较。这种方法是通过少量评价参数来比较各种小波基，但是实践表明传统的信息价值函数并不太适用。

2.2岩层破裂微震信号

由于岩层物质组成的独特性、岩石独特的地质形成过程导致岩层破裂微震信号具有特殊的波形特性。岩体在变形破坏的整个过程中几乎都伴随着裂纹的产生，扩展，摩擦，能量积聚，当内部能量积累到一定量之后，将以弹性波的形式释放出来。该信号的幅度是很大的，微震信号的很大一部将迅速达到峰值，然后逐渐衰减。在这个过程中，幅值从低到高变化，然后逐渐衰减，一个典型的岩层破裂微震信号如图1所示。

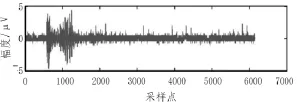
图1　一个微震信号的原始波形

2.3岩层破裂微震信号的小波基的选择

由于某些客观原因，导致在信号处理领域的还没有出现一个被大家认可的小波基的选择方法，也所以没有固定的模式可以遵循[11]。但是我们依旧能够分析岩层破裂微震信号的特性以及现有的小波基的优缺点。正如前面所讨论过的那样，岩层破裂微震信号不同于其他的微震信号，岩层破裂微震信号是一种时变的非平稳信号，具有不可预测性和突发性。与混凝土相比，一般岩体破裂微震信号强度很弱，而且频率也并不相同。不同的岩石，如砂岩、石灰石、煤等，在破坏过程中释放的信号频率也不同。因此所选择的小波基特性必须与岩层破裂微震信号一致。基于岩层破裂微震信号的特点，对小波基的选择需要考虑以下几点：

1）小波基必须具有可重构性，从而更有助于微震信号的获取。

虽然连续小波变换的尺度因子可以自由选择，也可以被用于时间-频率空间的分析，但是其重构公式复杂、计算量大。因此优先选择离散小波变换。因为正交小波能够通过适当的离散化形成正交基，所以非常适合用于分析计算量小、无冗余的信号。Mexican-hat小波和Morlet小波无论经过怎样离散化都不能形成正交或双正交基，并且具有较大的信号重构误差，所以这两种波一般不用于重构离散小波。

2）小波基必须适应于微震信号的动态特性和迅速衰减特性。

具有紧支性的小波基能够分析不同频率范围内的微震信号。由于Meyer小波没有紧支性，所以不适合用于微震信号的分析。

3）小波基必须能够从噪声中提取出有用信号。

由于噪声信号微震信号的影响极大，所以要求通过小波变换之后，小波基能有效的从噪声信号中识分离出微震信号[12]。相关研究表明，基于一阶消失矩的小波基可以有效地突出信号的奇异性。所以所选的小波基应该具有一阶消失矩。Morlet小波、Mexican hat小波和Meyer小波的基函数并不是一个好的选择。Haar小波基函数具有一阶消失矩，但它在微震信号分析中的适用性必须检查。

4）小波基必须适合于信号分析。

正交小波是非冗余，它们适用于去噪和对信号、图像的压缩。双正交小波用于提取信号和图像的特征，不适合微震信号的分析，所以Biorthogonal小波也不适合。

根据以上岩层破裂微震信号的特点，以及几种常见小波基函数的分析，Symlet和Coiflet小波基可以选择用于岩导破裂微震信号的分析。这两种小波基满足离散小波变换、时域紧支性、适当的消失矩、对称性的要求。

3　岩层破裂微震信号的小波分析

图1显示了一个岩层破裂微震信号的现场采集，包含大量的噪声。通过小波分析对信号进行降噪处理，首先使用上述分析的小波，Symlet和Coiflet小波基被用于岩层破裂微震信号的降噪处理。均方根误差（RMSE）是原始信号与降噪后的信号之间的方差的平方根，它反映了原始信号与降噪后的信号之间的差异[13]。在实际应用中，均方根误差越小说明它的降噪效果越好[14-15]。信噪比（SNR）是指原信号能量与噪声能量之比，信噪比越高，滤波效果越好[i]。

1）在保证其它外部条件不变的前提下，选用不同的Sym N小波进行降噪处理。信噪比（SNR）和均方根误差（RMSE）得到的结果如表2所示，可以发现Sym 8小波的降噪处理效果最好。因此选用Sym 8小波对岩层破裂微震信号进行处理和分析。

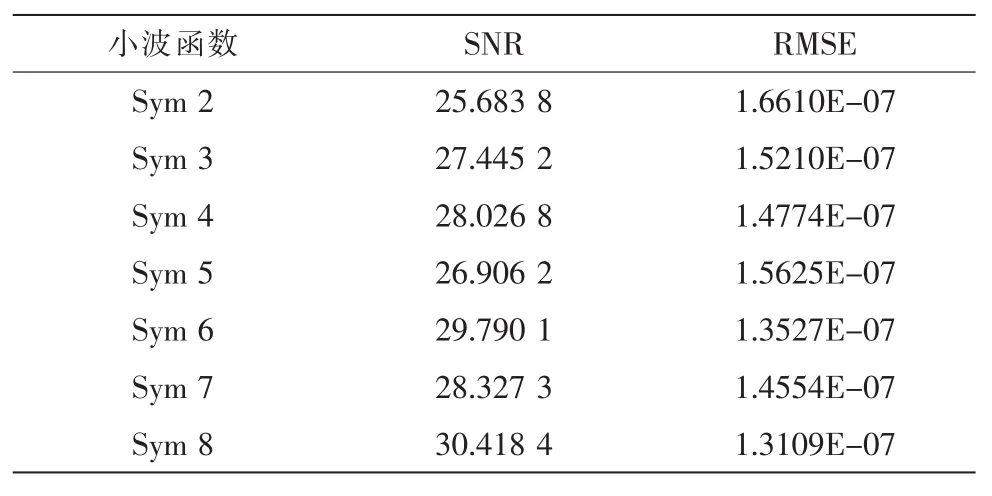
表2　SymN小波降噪的信噪比和均方根误差

2）在保证其它外部条件不变的前提下，选用不同的Coif N小波进行降噪处理。信噪比（SNR）和均方根误差（RMSE）得到的结果如表3所示，可以发现Coif 2小波的降噪处理效果最好，因此选用Coif 2小波对岩层破裂微震信号进行处理和分析。

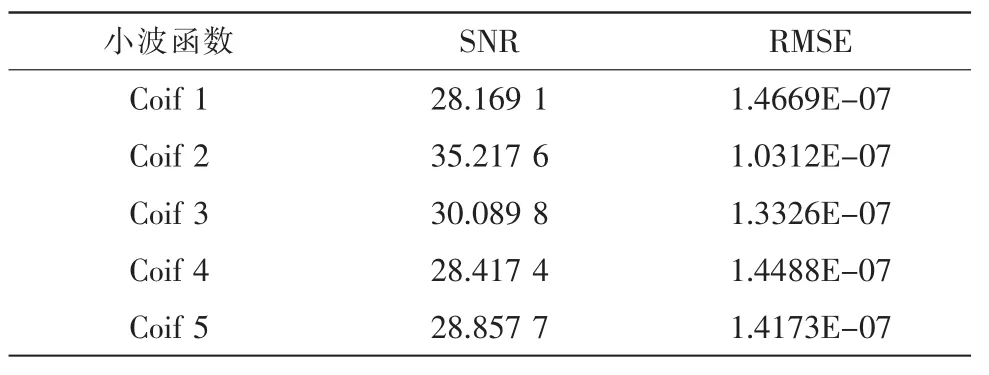
表3　CoifN小波降噪的信噪比和均方根误差

3）在保证其他外部条件不变的前提下，对同一个微震信号使用普通的dbN和Haar小波进行降噪处理。信噪比（SNR）和均方根误差 （RMSE）得到的结果如表4所示。与Sym 8和Coif 2进行对比，可以看出Sym 8和Coif 2的效果是最好的。所以Sym 8和Coif 2适合岩层破裂微震信号有处理和分析。

表4　6种小波降噪的信噪比和均方根误差

4　结　论

小波基函数的选取是信号小波变换的一个关键问题。通过对岩层破裂微震信号和常用小波基函数特点的分析，合适的小波基必须具有以下性质：紧支性、正交性、对称性和一阶消失矩。Symlet和Coiflet小波基适用于岩层破裂微震信号的处理。岩层破裂微震信号可以通过Sym 8和Coif 2小波基进行分解和降噪，通过相应的比较分析，确定它们的处理效果是最佳的。经过Sym 8小波处理后，信号的信噪比（SNR）和均方根误差（RMSE）分别为30.4184和1.3109e-07；经过Coif 2小波处理后，信号的信噪比（SNR）和均方根误差（RMSE）分别为35.2176和1.0312E-07。对岩层破裂微震信号进行小波分析时，Sym 8和Coif 2是合适的小波基。

[1]杨秀芳，张伟，杨宇祥.基于提升小波变换的雷达生命信号去噪技术[J].光学学报，2014，3（3）:292-297.

[2]龚斌，金文，李兆南，等.不同小波基在碳钢材料声发射信号分析中的应用[J].仪器仪表学报，2008，29（3）:506-511.

[3]唐守锋，童敏明，潘玉祥，等.煤岩破裂微震信号的小波特征能谱系数分析法[J].仪器仪表学报，2011，32（7）:1521-1527.

[4]何智龙，苏娟，覃芳.db2和db3小波变换的电力系统谐波联合分析[J].智能电网，2015，3（2）:129-133.

[5]张颖超，茅丹，胡凯.压缩传感理论在心电图信号恢复问题上的研究[J].计算机研究与发展，2014，51（5）:1018-1027.

[6]高忠社，何万生，谢保利.紧支撑样条小波插值及其应用[J].纯粹数学与应用数学，2013，29（6）:591-600.

[7]刘刚，张杨，李洁.小波帧变换方法在电能质量扰动中的仿真分析[J].上海电力学院学报，2012，28（5）:423-426.

[8]桑燕芳，王栋.水文序列小波分析中小波函数选择方法[J].水利学报，2008，39（3）:295-300.

[9]谢军，李乐，刘文峰.振动信号噪声消除中的小波基选择研究[J].科学技术与工程，2011，11（25）:5997-6000.

[10]金解放，赵奎，王晓军，等.岩石声发射信号处理小波基选择的研究[J].矿业研究与开发，2007，27（2）:12-15.

[11]周彦江，潘一山.基于小波变换的矿震信号去噪方法研究与应用[J].煤矿开采，2009，14（1）:29-31.

[12]钟孟春，张春林，李华，等.改进的小波包能量分段阈值降噪方法[J].计算机工程与应用，2013，51（5）:204-207.

[13]景新幸，冼灿娇，杨海燕.基于改进的小波阈值去噪算法的研究[J].电声技术，2015，39（5）:80-83.

[14]周西峰，朱文文，郭前岗.基于渐近半软阈值函数的超声信号去噪方法[J].探测与控制学报，2011，33（2）:35-39.

Selecting wavelet basis in wavelet transform analyses of rock rupture microseismic signal

WANG Qiang，CHEN Xun
（Jiangsu University of Science and Technology，Zhenjiang 212003，China）

The traditional signal analysis can only analyze the complete time-domain or complete frequency-domain，The wavelet can describe the local characteristics of signal time-domain（space）and frequency-domain.Wavelet transform is an important method in microseismic signals processing.However，different wavelet bases yield different results when analyzing the same signal.Through the analysis of the properties of commonly used wavelet basis functions and the characteristics of rock rupture microseismic to select the appropriate wavelet basis by calculating the results of signal-to-noise ratio（SNR）and the root mean square error（RMSE）.After Sym 8 wavelet denoising，the SNR and the RMSE were 30.4184 and 1.3109E-07，respectively.After Coif 2 wavelet denoising，the SNR and the RMSE were 35.2176 and 1.0312E-07，respectively.The results found that Sym 8 and Coif 2 wavelets are suitable for analyzing rock rupture microseismic signals.

wavelet analysis；wavelet base；microseismic signal；SNR；RMSE

TP911

A

1674－6236（2016）21-0126-03

2015-11-05稿件编号：201511048

王 强（1992—），男，安徽全椒人，硕士研究生。研究方向：嵌入式。