NURBS在电场计算中的研究
2016-11-21党伟孙雨
党伟+孙雨


摘要:在运用边界元方法计算开域场中的电场时,为提高传统一阶边界元法的精度问题,提出NURBS曲面四边形边界元法。此方法是对计算模型进行二阶四边形剖分,采用剖分信息构造出NURBS曲面参数方程,然后用面积比值法定义曲面上顶点的形状函数,曲面四边形的四个顶点作为求解点,计算NURBS曲面四边形单元上的积分值。
关键词:NURBS;电场强度;提高精度;电场计算;边界元法 文献标识码:A
中图分类号:TM151 文章编号:1009-2374(2016)29-0018-04 DOI:10.13535/j.cnki.11-4406/n.2016.29.008
边界元法在求解电磁数值计算中,是利用离散技术将求解的边界面离散为边界单元,将边界问题等价转化为边界积分方程问题,同时把边界积分方程离散为代数方程组,最后利用数值方法计算方程组,得到边界积分方程的解。
本文提出NURBS曲面四边形边界元方法。利用二阶剖分单元的节点信息,构造出NURBS曲面四边形单元,以曲面四边形单元的顶点为求解点,计算NURBS曲面四边形单元上的积分,最后形成NURBS曲面四边形边界元方法求解三维电场边值问题。
1 NURBS曲面边界元的基本原理
1.1 有理B样条基函数
NURBS(Non-Uniform Rational B-Spline)方法,是在B样条方法基础上发展起来的,为了能进一步精确地描述有理数,推广得到有理多项式基函数。将B样条基函数推广到有理的基函数,就得到了NURBS方法的基函数即有理B样条基函数,而且NURBS曲面在中心投影下得到B样条曲面,所以研究NURBS方法就必须了解B样条方法基础。
B样条函数的概念最初是由Schoenberg于1946年提出的。由de Boor-Cox公式得出提出B样条的递推公式为:
式中:称为相应于序列的次,即阶B样条基函数。其中,下标表示序号,下标表示次数。可以看出想要得到第个次B样条基函数,就得共个节点序列,而且的支撑区间为。由该定义出发,可以导出任意阶次的B样条基函数。文章中是采用高斯积分方法求解数值积分,由于高斯积分法对应的积分区间为。而在区间上B样条基函数为均匀的基函数,根据B样条基函数的性质,次B样条基函数只有个基函数在上非零,而且在上都为多项式函数。取,则由式(1)可得均匀2次B样条基函数表达式为:
有理B样条基函数作为对B样条基函数的推广,一个基函数变为有理分式首先需要相应的一个多项式作为分母,然而考虑到相同的分母将会给有理分式之间的计算带来简便。再注意到B样条基函数具有的“权”性,即在区间的非负性和单位分解性,因此可以采取下面的方法:给每一个B样条基函数乘以一个“权因子”,再用它们的“和”作为统一分母进行“平均”,这样就得到了次有理B样条基函数为:
1.2 NURBS曲面
NURBS曲面是非有理张量积型性B样条曲面的有理推广,类似于NURBS曲线定义,一张次NURBS曲面有理式可以表示为:
其中是双变量的有理基函数:
式中:为控制点;为与控制点相应的权因子;和分别为参数向次和参数向次的定义在和规范有理B样条基函数。
根据式(3),当时,得到广泛应用的双二次NURBS曲面的数学模型为:
上式中是由式(2)推导出,为的转置矩阵。
根据式(7),要得出NURBS曲面的参数方程,必须就算出控制点P11,P12,…,P33。根据有理式表示的NURBS曲面参数方程还可以表示为,其中为曲面数据点列,维数为;为有理基函数,维数为,为方阵,则逆矩阵存在;是控制点,维数为。在已知曲面上的数据点列,假定权因子时,经过矩阵求逆变换可得到双二次NURBS曲面控制点矩阵求逆变换可得。
1.3 四边形单元上的形状函数
本文是以四边形单元的四个顶点为求解点,运用面积比值法构造曲面四边形顶点上的形状函数。曲面单元如图1所示,曲面单元上任意一点处的函数值由4个顶点节点i、j、k、l上的函数值和点相对于4个顶点节点的形状函数插值得到。在图1中,点处的两条参数等值线将曲面单元分成、、、共4部分,其中每一部分的面积都可以通过曲面参数方程得到。设曲面单元总的面积为。则点处关于4个顶点的形状函数定义为:
1.4 边界元法
三维静电场光滑边界的积分方程为:
式中:为边界上的场点;为边界上的源点;为场点电位;为源点电位;为源点到场点的距离,;为边界外法线方向;S为求解区域的边界。
2 NURBS曲面边界元算例分析
2.1 算例一
如图2是高为2、半径为1的四分之一圆柱面。运用面积计算可知其表面积为。将其剖分一个单元,得出节点信息后,导入一阶平面四边形边界元程序计算其表面积为2.8284,相对误差为9.97%。将节点信息导入NURBS曲面边界元程序计算出四分之一圆柱面的表面积为3.1645,相对误差为0.073%。可以得出NURBS曲面边界元程序相比一阶平面四边形边界元程序精度提高了9.24%,所以NURBS曲面更接近实际的四分之一圆柱面,NURBS曲面边界元比一阶平面四边形边界元计算更加精确。
2.2 算例二
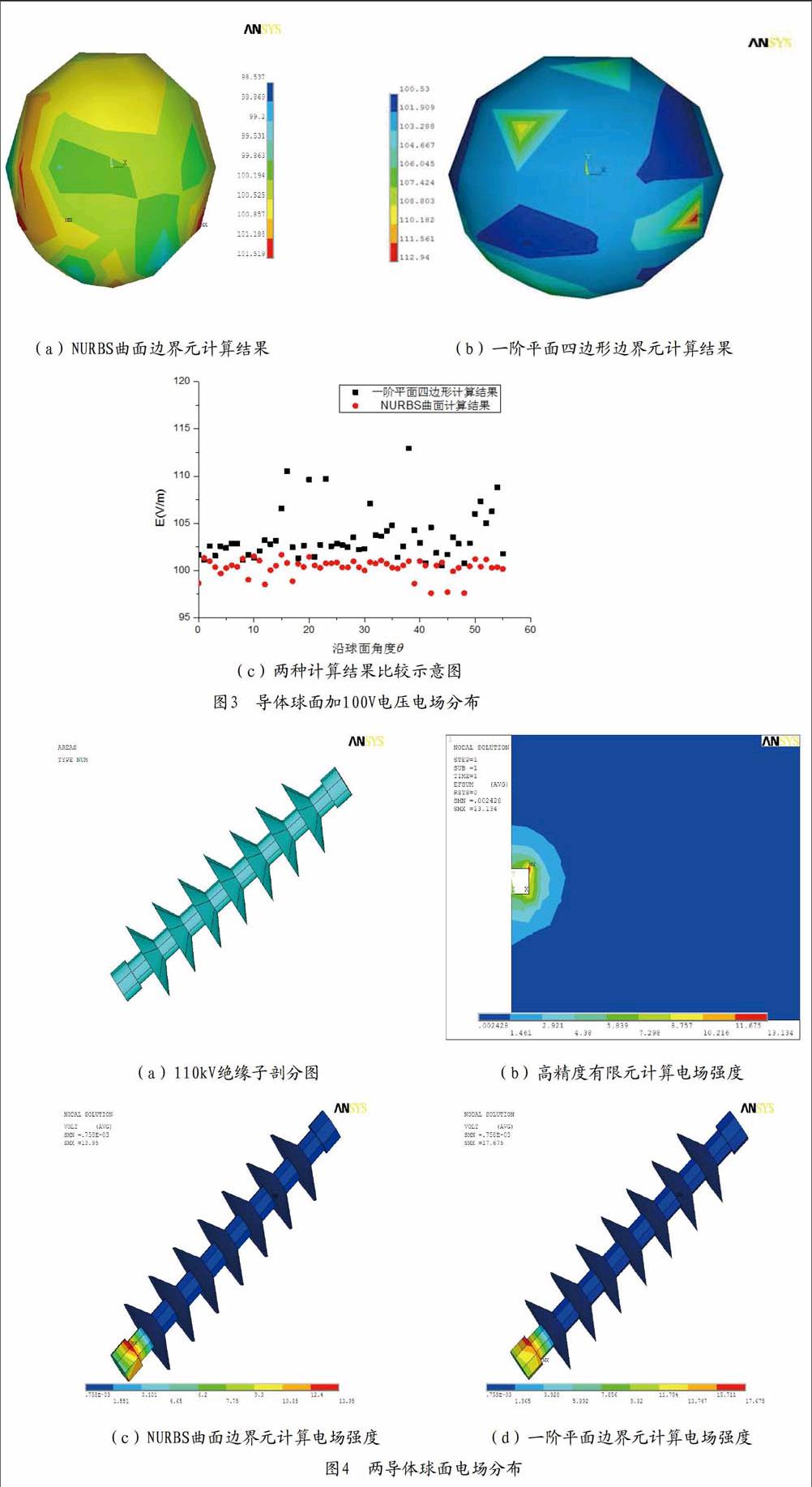
半径为1的导体球面,给导体球面加上100V电压,求解球面上的电场强度。用ANSYS建立球面模型,将其自由剖分54个单元,导出单元及节点信息代入NURBS曲面边界元程序计算各节点上的电场强度,结果云图如图3(a)。建立模型后进行一阶单元剖分,自由剖分为54个单元,代入一阶平面四边形边界元程序计算得出结果为图3(b)。将两种计算沿球面电场强度的结果在同一坐标系中呈现为图3(c)。
由电磁场知识得知半径为1m的导体球面加上100V电压,则球面上的电场强度为100V/m。NURBS曲面边界元计算结果最大相对误差为1.46%,一阶平面四边形边界元计算结果最大误差为12.94%。从两种计算得出沿球面上电场强度分布,可以得出NURBS曲面边界元计算结果基本上落在电场强度100V/m左右,节点分布相对规律。一阶平面四边形边界元计算结果距离电场强度100V/m偏差加大,节点分布相对零乱。所以可以得出在相同的剖分单元下,NURBS曲面单元拟合出的曲面更接近实际的球面,计算结果相对一阶平面也更加精确。
2.3 算例三
陶瓷绝缘子型号XP-120,绝缘子结构高度为146mm,建立该绝缘子模型后对边界面采用二阶四边形单元规则剖分240个单元,如图4(a)。高压端金具施加kV电压,低压端金具电压为0V。伞群和芯棒认为是一种介质,相对介电常数为6.0,分别用NURBS曲面边界元法和一阶平面四边形边界元法计算绝缘子的电场强度。为了验证边界元算法计算结果的正确性,根据轴对称可以用二维轴对称高精度有限元法(无限远处为零电位)计算绝缘子电场强度进行结果对比分析验证,单位为kV/mm。
由图4从数值可以看出,NURBS曲面边界元法计算的绝缘子上最大电场强度为13.95kV/mm,高精度有限元计算结果为13.134kV/mm,一阶平面四边形边界元法计算结果为17.675kV/mm。对比图4(b)、图4(c)、图4(d)可知,NURBS曲面边界元法与高精度有限元算法计算结果基本一致;一阶平面四边形边界元法计算结果相对误差为34.5%左右,可以得出NURBS曲面边界元法比一阶平面四边形边界元法明显的精度提高。边界元算法只需要对求解模型的边界进行剖分,求解的规模明显小一些,这也是边界元法相比有限元法的优势。
3 结语
相比于传统的边界元法,提出了NURBS曲面四边形边界元方法,该方法在不增加节点的情况下提高边界元方法计算的精度。通过算例表明,该方法比传统一阶平面单元更逼近实际边界,既提高了精度,又没有增加节点数,达到了比较理想的效果。
参考文献
[1] 姚振汉,王海涛.边界元法[M].北京:高等教育出版社,2010.
[2] 王仁宏,李崇军,朱春钢.计算几何教程[M].北京:科学教育出版社,2008.
[3] 施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001.
[4] 李亚莎,王泽忠.基于圆环坐标系的三维静电场曲面三角形边界元法[J].电工技术学报,2006,21(9).
作者简介:党伟(1975-),男,湖北十堰人,国网湖北省电力公司十堰供电公司高级工,助理工程师。
(责任编辑:黄银芳)
