基于量子布谷鸟搜索的认知无线网络频谱分配

2016-11-20王先平曹卉

电信科学 2016年5期

关键词：鸟窝布谷鸟频段

王先平，曹卉

（1.重庆文理学院软件工程学院，重庆 402160；2.河南广播电视大学现代教育技术中心，河南郑州 450000）

基于量子布谷鸟搜索的认知无线网络频谱分配

王先平1，曹卉2

（1.重庆文理学院软件工程学院，重庆 402160；2.河南广播电视大学现代教育技术中心，河南郑州 450000）

为了有效解决认知无线网络频谱分配的离散优化问题，将量子计算引入布谷鸟搜索算法，提出了一种新的组合优化算法——量子布谷鸟搜索算法。该算法使用量子鸟窝表征问题的多维解，通过Lévy flights随机游动方式和量子突变策略快速搜索到全局最优位置。通过使用基准函数验证了算法的高效性，并提出了一种基于量子布谷鸟搜索的认知无线网络频谱分配方法。然后与经典频谱分配算法在不同的网络效益函数下进行仿真性能比较。结果表明，所提出的频谱分配方法能够较快找到全局最优解，并且在不同网络效益函数下均优于已有的经典频谱分配算法。

认知无线网络；频谱分配；离散优化问题；量子计算；布谷鸟搜索算法

1 引言

随着无线通信技术的快速发展，无线频谱资源愈发紧缺，成为通信业务发展的瓶颈［1］。认知无线电网络（cognitive radio network，CRN）作为下一代通信网络，能够高效解决频谱资源浪费问题，成为国内外研究者的关注热点［2］。在认知无线网络中，次级用户（非授权用户）可通过频谱感知模块实时感知电磁空间的频谱利用情况，在不影响主用户（授权用户）正常通信的前提条件下动态占用空闲频谱，提高频谱利用效率。目前应用认知无线网络的主要频谱算法有图着色（color sensitive graph coloring，CSGC）［3］、博弈论［4］和拍卖理论［5］等。其中基于图着色法的认知无线网络频谱分配模型由于可以根据实际需要选取不同的效益函数，近年来得到广泛应用和研究［6］。

为了解决频谱分配优化问题，很多研究将量子计算引入传统群智能算法，提出了量子遗传算法（quantum genetic algorithm，QGA）［7］、量子粒子群优化（quantum particle swarm optimization，QPSO）［8］算法和量子蜂群（quantum artificial bee colony，QABC）［9］算法等。以上群智能算法在解决低维优化问题时具有快速和有效的优化性能，但针对频谱分配这种具有高维度解的优化问题，其收敛速度和性能受到严重挑战。2009年，Yang等人［10］提出了粒子群的变种算法——布谷鸟搜索算法（cuckoo search algorithm，CSA）。CSA不仅具有参数少、计算简单和易于实现的特点，而且其收敛性能优于遗传算法、粒子群算法和量子蜂群算法［11，12］。但由于CSA只能解决连续优化问题，并不能解决离散组合优化问题。

本文基于布谷鸟搜索算法，首次引入量子计算，提出了一种新的群智能优化算法——量子布谷鸟搜索算法（quantum cuckoo search algorithm，QCSA）。该算法首先使用量子比特表征问题潜在解，通过布谷鸟种群搜索空间找到问题的最优解。其次，提出了基于量子布谷鸟搜索算法的认知无线网络的频谱分配算法，并验证了分配算法的有效性。结果证明，相比于传统群智能优化算法，本算法具有高效的收敛速度和优化性能。

2 量子布谷鸟搜索算法

标准布谷鸟搜索算法将对鸟窝位置的搜索空间视作可行域，将鸟窝位置视作潜在解，将最优的鸟窝位置作为优化问题的最优解，进而建立布谷鸟种群和解集之间的关系。由CSA服从的3条基本原则［13］可知，鸟蛋代表问题解，并且每只布谷鸟在每次迭代过程中只能占用一个鸟窝并生产一颗蛋，这是最简单的情况。当然可以通过扩展蛋的生产数目来解决多目标优化问题。但本文仍基于这种最简单的情形，因为布谷鸟、鸟窝和蛋的数目相同，在后文的描述中三者可以等同，均表示问题的解，为便于理解，后文将使用量子鸟窝位置代表问题的解。

2.1 量子鸟窝表征问题解

量子计算是一种双状态的量子系统，不同于传统的二进制系统，其状态可以落在状态和的任一线性组合状态上。因此，量子比特状态可表示为：

量子鸟窝位置由量子比特组成的向量表示，向量中元素的数目取决于问题解的维数。在QCSA中，量子鸟窝i被定义为：

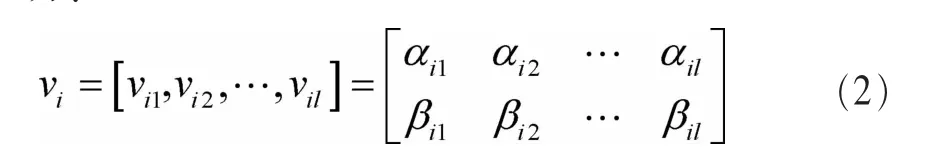
其中，|αij|2+|βij|2=1，且 0≤αij，βij≤1。

种群测量是指将量子向量转换为二进制向量的过程，如图1所示。问题潜在解必然存在于量子状态集合的某一个状态，需要通过量子测量确认此解的状态，通过二进制比特表示其解的稳定状态。量子测量并不会破坏量子鸟窝的量子位置，量子位置会被保存至下一次迭代。量子比特对应的二进制值可以通过量子比特的状态概率|α|2和|β|2计算得到。其量子比特测量主要过程为：算法会针对某量子比特生成一个介于0和1之间的随机数randi，如果randi≥|α|2，则量子比特值为 1，否则为 0，表示如下：

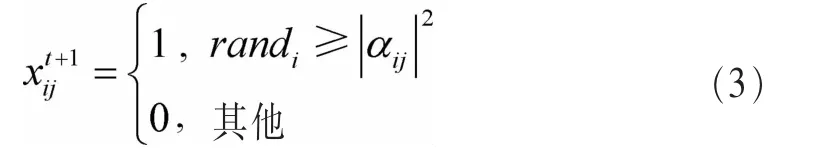
同时，量子鸟窝的量子位置测量式为：

2.2 QCSA算法描述

QCSA的搜索过程主要由种群初始化、择优选择和随机迁移构成，通过更新进化布谷鸟种群的量子窝位置，找到全局最优的量子鸟窝位置。每只布谷鸟选择的量子鸟窝代表优化问题的一个潜在解，通过适应度函数来评估潜在解，找到最优解。

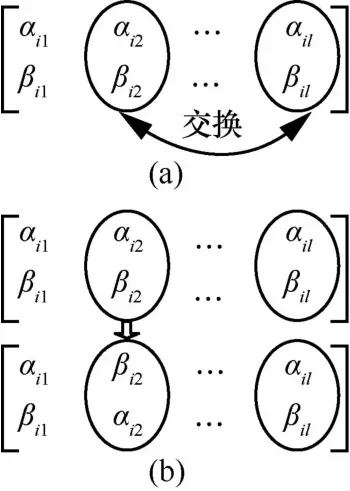
图1 量子突变策略示意

（1）种群初始化

假设进化种群共有h只量子布谷鸟（对应相同数目的量子鸟窝），并且量子鸟窝的量子位置和测量位置（用二进制比特表示）的维数是 l。因此，量子位置集合为 υ=｛υ1，υ2，…，υh｝，测量位置集合为 x=｛x1，x2，…，xh｝。t次迭代过程中量子窝i的量子位置表示为，经过量子测量后获得的测量位置，且有i=1，2，…，h。

（2）择优选择

在择优选择过程中，每只量子布谷鸟通过Lévy flights随机游动方式和量子突变策略搜索更新量子鸟窝的量子位置，通过量子测量得到测量位置。t次迭代后所有量子窝中的全局最优位置为，表示搜索至今所有局部最优值中的最优解。种群进化是指量子鸟窝位置更新，设量子旋转角度为，量子旋转门为，其表达式为：

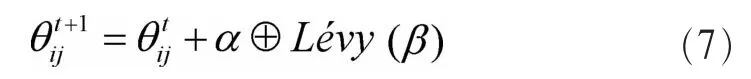
在式（7）中，a 为搜索步长，Léυy（β）是 Lévy 飞行随机游动方式的概率函数，⊕指点乘积。为便于计算，Léυy（β）表达式为：

其中，u和r均服从正态分布，且有：

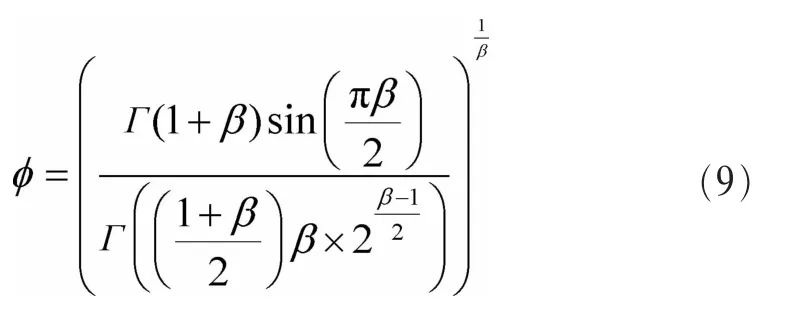
其次，采用量子突变策略来增强潜在解的多样性。当某量子窝满足或生成小于变异概率pm的随机数时，QCSA采用量子比特间交叉变异和量子比特内突变以增强种群多样性，过程如图1所示。量子比特内突变使用量子非门，其量子旋转角度=0，表达式为：

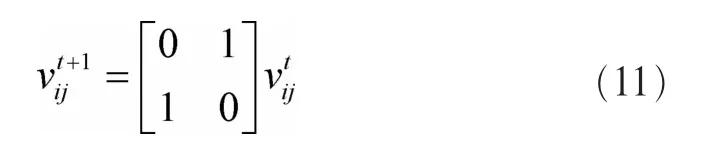
（3）随机迁移

QCSA会通过发现概率pa放弃部分劣质解，同时使用Lévy飞行随机游动方式随机生成相同数量的解，进而增加种群多样性，避免陷入局部过优。量子布谷鸟算法的主要步骤如下。

开始

种群初始化（随机生成h只量子鸟窝）

While（停止准则）

·使用Lévy飞行路径随机更新量子鸟窝；

·使用量子变异策略；

·测量量子鸟窝；

·评估量子鸟窝；

·以发现概率pa放弃部分劣质解并生成相同数量的新解；

·保持优质解至下一代；

·通过适应度函数值评估对量子鸟窝排序，求得最

优解。

End While

结束

3 基于QCSA的认知网络频谱分配方法

3.1 认知网络频谱分配模型

设在认知无线网络中有N个次级用户去竞争主用户未占用的M个空闲正交频段的使用权。认知无线网络频谱分配模型主要由可用频谱矩阵L、干扰矩阵C、效益矩阵B和无干扰分配矩阵A组成［14，15］。

可用频谱矩阵 L=｛ln，m|ln，m∈｛0，1｝｝N×M表示次级用户n在不影响相邻授权用户正常通信的条件下是否可以使用频段m。如果次级用户n使用频段m不影响其他授权用户，则令 ln，m=1；否则，令 ln，m=0。

干扰矩阵 C=｛ln，k，m|ln，k，m∈｛0，1｝N×N×M表示用户 n 和 k 使用频段m的干扰情况。如果ln，k，m=1，表示用户n和k同时使用频段 m时会互相干扰；如果ln，k，m=0，表示用户n和 k同时使用频段m时不会互相干扰。同时，干扰矩阵与可用频谱矩阵也有制约关系，即 ln，k，m≤ln，m×lk，m。当 n=k 时，cn，k，m=1-ln，m。

效益矩阵 B=｛bn，m｝N×M表示次级用户 n 使用频段 m 的效益，效益正比次级用户的覆盖范围，可以用资源利用率、吞吐量、最大流量等描述。如果 ln，m=0，则 bn，m=0。

无干扰分配矩阵A给出了一种可行的频谱分配方案，表达式为 A=｛an，m|an，m∈｛0，1｝｝N×M。如果将频段 m 分配给次级用户 n，则 an，m=1。最后，矩阵 A必须满足的干扰约束条件为：

若cn，k，m=1，∀1≤n，k≤N，1≤m≤M，每个次级用户n获得的效益rn定义为：

所有次级用户组成的效益矩阵为 R=｛rn｝N×1，所有可行的频谱分配方案集合为 Λ（L，C）N×M，无线电频谱分配方案的目标就是从此集合中找到使网络效益优化目标函数U（A）最大的分配方案A*。

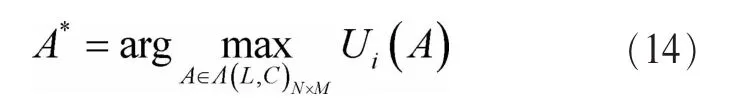
其中，i∈｛MSR，MPF｝。

最大网络效益和函数UMSR（A）为：

式（15）是为了获得最大的平均网络效益，并未考虑用户接入的公平性。

最大比例公平网络效益函数UMPF（A）定义为：

式（16）中每个用户的初始效益为1×10-6。

3.2 基于QCSA的认知网络频谱分配方法

无干扰频谱分配矩阵A受限于可用频谱矩阵L，如果ln，m=0，则对应矩阵中的元素 an，m必为 0。为了减小计算量，仅将L中值为1的元素位置对应的矩阵A中的元素构成量子布谷鸟量子鸟窝的量子位置。量子布谷鸟搜索算法中所有量子比特初始值均设为在本文中QCSA的适应度指网络效益函数值，通过求取最大网络效益函数值来获得问题的最优解。具体频谱分配方案步骤如下所述。

步骤2 初始化量子布谷鸟群，设有h只量子布谷鸟。初始化量子鸟窝的量子位置，测量得到量子鸟窝的二进制表示的测量位置，同时得到初始的局部最优值。

步骤3 首先将量子鸟窝测量位置的第j位比特映射到无干扰分配矩阵A的an，m。然后针对所有频段m，寻找干扰矩阵 C中所有满足 cn，k，m=1并且 n≠k的元素，再对应检查 A矩阵的 an，m和 ak，m是否都为 1：如果是，则随机将其中一个设置为0，同时改变矩阵测量位置中对应的比特值。

步骤4 计算量子鸟窝测量位置的适应度，确定每只量子布谷鸟的局部最优位置，同时确定种群到现在为止找到的全局最优位置。

步骤5 判断是否达到最大迭代次数：如果是，则迭代结束，将得到的全局最优解转换成无干扰分配矩阵A；否则，进行下一步。

步骤6 随机放弃部分劣质解，并生成相同数目的新解。

步骤7 保存最优解至下一代。

步骤8 使用Lévy flights随机游动方式和量子突变策略更新种群的量子鸟窝的量子位置，并转至步骤3。

4 仿真结果和分析

本节首先仿真了QCSA和QGA、QPSO、QABC传统优化算法在某典型测试函数作为目标函数条件下的性能比较，然后在不同网络效益函数下仿真了基于QCSA的频谱分配方法，并和基于 CSGC、QGA、QPSO和 QABC等传统优化算法的频谱分配方法进行了性能比较。为便于性能比较，所有试验中每个优化算法的种群规模和迭代次数均相同，其中，种群规模为50，终止迭代次数为1 000次，仿真试验结果采用200次独立的最优网络效益的统计平均值。除了文中设置的参数，传统优化算法的参数设置见参考文献［6-9］。QCSA算法的主要参数为：搜索步长 a=0.01，变异概率 pm=0.2，发现概率 pa=0.25。

4.1 基于SchwefeI函数的QCSA性能测试

经典测试函数Schwefel［16］公式为：

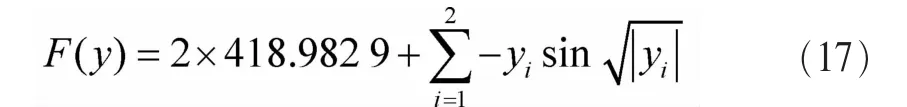
其中，-500≤yi≤500，i=1，2。

由于Schwefel函数是具有大量局部最优点的复杂多峰非线性函数，因此经常用于优化算法的收敛性能测试，测试曲线如图2所示。优化算法的收敛性能优劣排序为QCSA＞QPSO＞QABC＞QGA。其中，本文所提算法 QCSA的收敛速度和收敛性能远远优于其他传统算法。而QPSO、QABC和QGA具有相近的收敛性能，均易陷入函数的部分局部解中。

图2 QCSA性能测试曲线

4.2 基于最大网络效益的性能仿真

设认知无线电网络中主用户数目为15，次级用户数目为15，可用频段数目为15。图3为不同频谱分配算法以最大网络效益为优化目标的性能曲线。由图4可知，CSGC算法性能最差，平均网络效益固定不变；其他算法如QPSO、QABC和QGA等易早熟，容易陷入局部解中，而本文所提的QCSA算法的收敛速度和收敛精度明显优于其他3种优化算法。

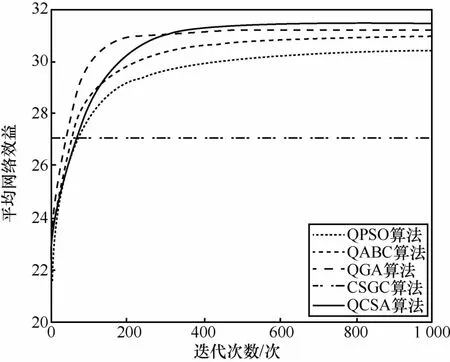
图3 基于最大网络效益的性能比较

为分析在相同条件下可用频段数目对网络效益的影响，设次级用户数目为10，其中，主用户数目和频段数目相同，增加频段数目以研究平均网络效益的变化情况，表1为仿真结果。随着频段数目的增加，次级用户获得的频谱资源在增加，因此平均网络效益也逐渐增加。并且可知使用QCSA的网络效益优于其他算法。

表1 不同频段数目对最大网络效益的影响

当可用频段数目和主用户数目不变时，考虑不同次级用户数目对平均网络效益的影响，设频段数目为10，结果见表2。随着次级用户数目的增加，网络中的频段使用权竞争激烈，平均网络增益下降，但QCSA性能仍优于其他算法。

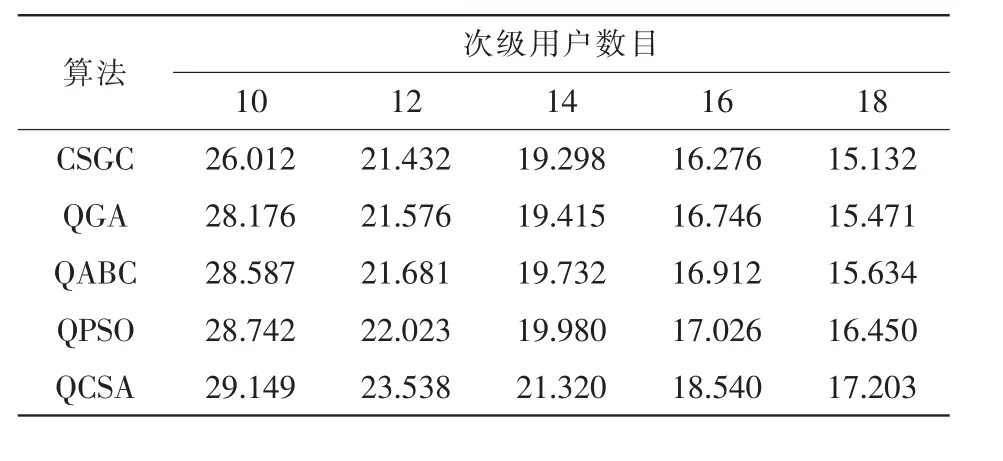
表2 不同次级用户数目对最大网络效益影响

4.3 基于最大比例公平网络效益的性能仿真

设认知无线网络中主用户数目、次级用户数目和可用频段数目均为15。图4为不同频谱分配算法以最大比例公平性网络效益为优化目标的性能曲线。由图5可知，CSGC算法的性能很差，其他优化算法容易陷入局部最优，而本文所提的QCSA算法具有较好的收敛性能，能够更好地寻找到最优解。

图4 基于最大比例公平性网络效益的性能比较

设次级用户数目为10，逐渐增加主用户和可用频段数目，分析频段数目对最大比例公平性网络效益的影响，仿真结果见表3。随着可用频段数目的增加，次级用户可以使用的网络资源在增加，因此网络中次级用户可以获得更公平的频段接入，并且QCSA的最大比例公平性网络效益优于其他算法。

表3 不同频段数目对最大比例公平性网络效益的影响

保持主用户和可用频段数目为10，逐渐增加次级用户数目，研究次级用户数目对最大比例公平性网络效益的性能影响，数值结果比较见表4。QCSA算法性能优于其他传统算法，且随着次级用户数目的增加，频段使用权竞争激烈，用户接入公平性降低。

表4 不同次级用户数目对最大比例公平性网络效益的影响

5 结束语

本文提出了量子布谷鸟搜索优化算法，使用Schwefel函数验证了算法的有效性。同时提出了基于QCSA的认知无线网络频谱分配方法，旨在解决以最大网络效益函数和最大比例公平性网络效益函数为优化目标的频谱分配问题。仿真结果表明，相比传统优化算法，本文所提方法可以获得更好的网络效益性能。下一步的工作是运用量子布谷鸟搜索算法解决认知无线电网络的决策引擎和频谱感知等问题。

［1］AKYILD Z，LI W.Next generation／dynamic spectrum access／cognitive radio wireless networks：a survey ［J］.Journal of Computer Networks，2013，9（2）：2127-2159.

［2］JOSEPH M.Cognitive radio for flexible mobile multimedia communication ［C］／Sixth International Workshop on Mobile Multimedia Communications，Nov 15-17，1999，SanDiego，CA，USA.New Jersey：IEEE Press，1999：3-10.

［3］廖楚林，陈吉，唐友喜，等.认知无线电中的并行频谱分配算法［J］.电子与信息学报，2007，29（7）：1608-1611.LIAO C L，CHEN J，TANG Y X，et al.Parallel algorithm of spectrum allocation in cognitive radio networks ［J］.Journal of Electronics&Information Technology，2007，29（7）：1608-1611.

［4］WANG B B，WU Y L，LIU K J R.Game theory for cognitive radio networks：an overview［J］.Computer Networks，2010，54（14）：2537-2561.

［5］KIM S.Trust-based bargaining game model for cognitive radio spectrum sharing scheme ［J］. IEICE Transactions on Communications，2012，E95-B（12）：3925-3928.

［6］PENG C，ZHENG H，ZHAO B Y.Utilization and fairness in spectrum assignment for opportunistic spectrum access［J］.ACM Mobile Network and Applications （MONET），2006，11 （4）：555-576.

［7］赵知劲，彭振，郑仕链，等.基于量子遗传算法的认知无线电频谱分配［J］.物理学报，2009，58（2）：1358-1363.ZHAO Z J，PENG Z，ZHENG S L，et al.Cognitive radio spectrum assignment based on quantum genetic algorithm ［J］.Acta Physica Sinica，2009，58（2）：1358-1363.

［8］GAO H Y，CAO J L.Non-dominated sorting quantum particle swarm optimization and itsapplication in cognitive radio spectrum allocation ［J］.Journal of Central South University，2013，20（7）：1878-1888.

［9］高洪元，李晨琬.膜量子蜂群优化的多目标频谱分配［J］.物理学报，2014，63（12）：128801-128812.GAO H Y，LI C W.Membrane-inspired quantum bee colony algorithm for multi objective spectrum allocation ［J］.Acta Physica Sinica，63（12）：128801-128812.

［10］YANG X S，DEB S.Cuckoo search via Lévy flights［C］／World Congress on Nature&Biologically Inspired Computing，December 9-11，2009，Coimbatore，India.［S.l.：s.n.］，2009：210-214.

［11］YANG X S，DEB S.Engineering optimization by Cuckoo search［J］.International Journal of Mathematical Modeling and Numerical Optimization，2010，1（4）：330-343.

［12］CIVICIOGLU P，BESDOK E.A conceptual comparison of the cuckoo search， particle swarm optimization， differential evolution and artificial bee colony algorithms ［J］.Artificial Intelligence Review，2013，39（4）：315-346.

［13］宋玉坚，叶春明，黄佐研.基于克隆布谷鸟算法的资源均衡优化［J］.计算机应用研究，2014，31（5）：1324-1327.SONG Y J，YECM，HUANG ZY.Resourceleveling optimization based on clonalcuckoosearch algorithm ［J］.Application Research of Computers，2014，31（5）：1324-1327.

［14］柴争义，刘芳.基于免疫克隆选择优化的认知无线网络频谱分配［J］.通信学报，2010，31（11）：92-100.CHAI Z Y，LIU F.Spectrum allocation of cognitive wireless network based on immune clone selection optimization ［J］.Journal on Communication，2010，31（11）：92-100.

［15］彭振，赵知劲，郑仕链.基于混合蛙跳算法的认知无线电频谱分配［J］.计算机工程，2010，36（6）：210-213.PENG Z，ZHAO Z，ZHENG S L.Cognitive radio spectrum assignmentbased on shuffled frog leaping algorithm ［J］.Computer Engineering，2010，36（6）：210-213.

［16］张勇，夏树发，唐冬生.果蝇优化算法对多峰函数求解性能的仿真研究［J］.暨南大学学报（自然科学与医学版），2014，35（1）：82-87.ZHANG Y，XIA S F，TANG D S.Simulation of multi-peak function based on the fly optimization algorithm ［J］.Journal of Jinan University （Natural Science&Medicine Edition），2014，35（1）：82-87.

Spectrum allocation based on quantum cuckoo search algorithm in cognitive radio network

WANG Xianping1，CAO Hui2
1.School of Software Engineering，Chongqing University of Arts and Sciences，Chongqing 402160，China 2.Modern Education Technology Center，Henan Radio&Television University，Zhengzhou 450000，China

There are discrete optimization problems for spectrum allocation in cognitive wireless network.A novel combinatorial optimization algorithm called quantum cuckoo search algorithm （QCSA）was proposed，which was based on quantum computing and cuckoo search algorithm.The quantum nest was used to represent multiple dimensionality solution for the optimization problem，and the global optimal position was found according to Lévy flights and quantum mutation strategy.In additional，some classical benchmark functions were employed to prove the effectiveness of QCSA，and a spectrum allocation method based on QCSA was proposed for cognitive network.Compared with classical spectrum allocation methods by using different network utility functions，the global optimal solution can be searched so fast.Simulation results show that the proposed spectrum allocation method based on QCSA is better than other traditional methods under different network utility functions.

cognitive wireless network，spectrum allocation，discrete optimization problem，quantum computing，cuckoo search algorithm

s：Henan Provincial Department of Science and Technology Project “the Public Service Platform of Massive Digital Resources of Henan Lifelong Education Based on Cloud Storage”（No.152102210304），Henan Provincial Department of Education Project “Research on Storage Management of Massive Digital Teaching Resources for Community Distance Education in Henan”（No.ZJA15172）

TP311

10.11959／j.issn.1000-0801.2016125

2016-03-09；

2016-04-08

河南省科技厅基金资助项目“基于云存储的河南省终身教育海量数字化资源公共服务基础平台建模研究”（No.152102210304）；河南省教育厅基金资助项目“面向河南省社区远程教育的海量数字化教学资源存储管理研究”（No.ZJA15172）