在初中数学活动课折纸教学中学习尺规作图

王相飞

【摘 要】新课程改革后，教材对学生学习尺规作图的要求是：理解作图原理和掌握使用作图工具技能。尺规作图要求教师教学中把握适当的尺度，教学中的难度主要是学生的实际操作。学生在基本作图法的单项应用是可以训练的，但是对于基本作图法的综合应用和考察思维能力上有明显的缺陷。这与传统的数学课堂教学的严肃、枯燥，教学形式单一有一定关系。笔者通过设计折纸教学活动，让学生亲自动手参与实践，调动学生的学习兴趣，同时也丰富了师生教与学的方式。

【关键词】折纸；尺规作图；教学方式

一、设计活动课的背景

在初三的总复习学到图形操作实践专题时，我给学生们准备了一道有关圆的作图题，如图，直线AB、直线CD是不平行的两条直线，现在作圆O与直线AB、直线CD都相切，以下是甲、乙两名同学的作法：

（甲）（1）过点D，作直线L与直线AB垂直，且交直线AB于F

（2）取DF中点O

（3）以O为圆心，OF长为半径画圆，则圆O即为所求。

（乙）（1）设直线AB与直线CD相交于Q。

（2）作DQB的角平分线。

（3）过点C，作一直线M与直线CD垂直，且交直线L于O。

（4）以点O为圆心，线段OC长为半径画圆，则圆O即为所求。

师：对于甲、乙两位同学的作法，同学们怎么看？

当各小组的答案纸收来批改时，学生们的表现很让我惊讶，是什么原因会让学生课堂的效果如此不理想。我顿时陷入沉思，分析原因，寻找对策。

在查阅复习资料后，经过比对，发现圆的作图是个教学难点，再加上与角平分线、中线的结合，只有少数优秀的学生能够独立完成，其他同学在老师或同学的帮助下才能完成。如何有效地解决学生解题困惑，这是我思考尺规作图课堂改变教学模式的起点。

用分析、猜想等手段去学习几何作图，是一条重要的途径，从学生的几何作图基础及生活的经验作为思考的起点，重新设计几何作图的课堂教学方式。

二、设计活动课的目的

（1）在折纸情景中，把角平分线和中垂线等知识墨化到基本图形的性质判定中去。

（2）使学生在折纸活动中，能联系几何图形变换，激发学习的兴趣。从而让大部分学生能简洁地使用工具，例如：直尺、圆规作角平分线。

（3）充分挖掘学生想象力，让作图工具特性所产生的效果是学生无法在日常生活经验积累中得到。在折纸活动中让学生意识到作图工具动作虽然有限，但可以变化出很多应用，掌握作图步骤。

三、折纸活动课教学过程

1.情景引入——童年的回忆

师：同学们，你们还记得在小时候和伙伴们一起玩折纸游戏吗？比如折纸飞机、小纸船等都有意思。我们在平时接触比较平常的纸张是书本、作业本、稿纸、打印纸等，它们的形状都是长方形的。如第一个图，折起一个角，就得到了一个直角三角形。要求学生拿起纸张模仿，使学生联想到游戏中的折纸方法。

折纸飞机这个过程中，重复地应用对称和平分的概念，体验数学之美。

2.设置折纸问题

折纸能用来指导作图吗？这是很多人曾经难以释怀的问题，数学家yates指出所有欧氏几何作图问题本质上均为寻找所有交点的相对位置。折纸动作所产生的折痕视为直线，多边形纸张的边亦视为直线，经纸张折叠后可重合的两线段或两角都视为相等。当一个作图问题中所有交点的相对位置都确定后，此作图问题可视为完成。

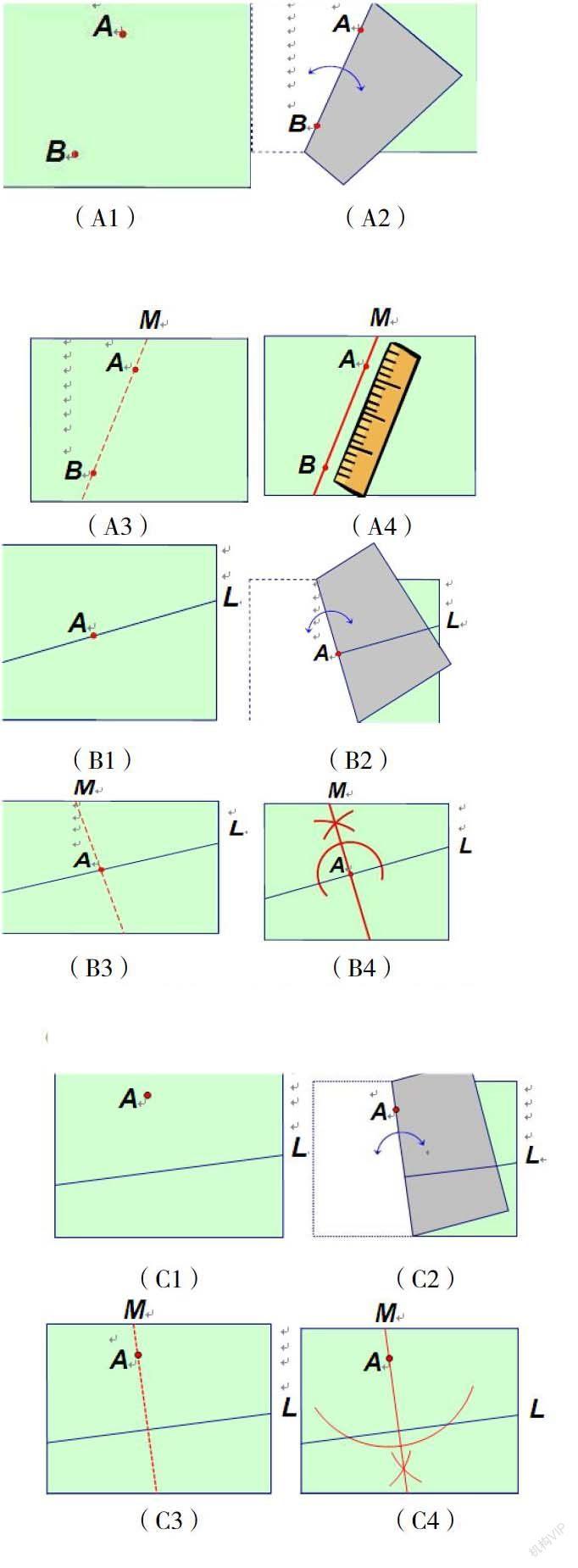
活动一：折出通过两点的直线

师：请看幻灯片展示的题目要求

（学生以学习小组为单位，观察、尝试、探索折纸的方法，发表学生的观点，由两个同学来评价。）

教师展示如图A1、A2、A3。

转化：尺规作图可用直尺画线如图A4，让学生初步感受折纸与尺规作图的联系。

活动二：在直线L上取一点，A，过点A作直线L的垂线。

教师要求学生在纸上画好题目的几何语言，有了前一题的体会，学生的表现好了很多，折纸的速度也加快了。各小组汇报折纸情况后，邀请学生作评价。展台展示图B1、B2、B3。

通过活动二的折纸让学生体会垂线的作法以及对折的意义，及时展示图B4。

活动三：过直线外一点向已知直线L引垂线。

教师在引导学生做活动三时，由于难度提升，刻意提醒直线重合，学生顺利达到预期目标，各学习小组汇报后，展台展示图C1、C2、C3。

在原对折的基础上加深为直线的重合，图C4的展示让学生对折与中垂线的联系，中垂线尺规作图理论依据在图C2中体现清晰。

活动四：在直线L上取一点A′，使得AB=BA′.

师：现在，我们考虑线段相等的折纸操作是如何实现的。在折纸时注意图中线段的位置和线段长度的关系。

学生发现：折纸时，点A在L上是关键（图D1、D2、D3）。

师：请同学们将折纸打开，用笔描上，用心体会折纸对应点的意义，以及用圆规使用的线段特征（图D4）。将对应定点的连线段大小关系和圆规的使用特征进行比较。

得出结论：利用圆规复制线段。

活动的目的是让学生折叠角度得到角平分线的概念。当展台显示题目内容后，还没等教师提示学生就异口同声的回答出答案。折法如图E1、E2、E3所示。

如图E4所示，通过圆规三次画弧，取两组线段相等，从而得出三角形全等（SSS），证明尺规作图角平分线的正确性。而两条直线折叠，处处显示线段相等，至于长度取值随宜。

活动六：交流体验

师：这节课同学们知道了什么？有什么体会和困惑吗？

生：折纸蕴含很多数学道理，感觉数学就在生活中。以前在学习中垂线和角平分线的画法，虽然会画，但不知其原理，今天终于明白了。

整个课堂活动都以折纸——讨论——展示——反思作图的顺序重复进行，让学生通过折纸体会尺规作图的理论依据，反思作图困难的原因。让学生相互辩论和说明，形成合作、竞争的良好学习氛围。

最后教师布置一道课外作图题，让学生将折纸学到的知识来破解。

如图F1，已知△ABC，请利用尺规作图作出筝形BPQR，使得P、Q、R分别在AB、AC、BC上符合题目条件的草图

由折纸帮助思考，折纸过程中重复应用对称概念，可引导学生观察草图的对称性质。筝形为线对称图形，对角线BQ为其对称轴。

四、折纸活动课的教学反思

从折纸活动课的教学过程中，经历了情景设置、问题设置、结论归纳、交流体验、作业等各环节，通过各环节把折纸的理论依据提炼出来，指导尺规作图的实施。从教学方式看，本节课主要强调学生从实际生活经历出发，在折纸活动中学习尺规作图，但是此项活动毕竟只限于对纸张的翻折和设计，停留在表面，这就需要教师正确地引导使学生从直观操作到抽象思考转变，师生同时感受数学目前已经成熟的操作方式的发现历程，不仅丰富了学生的情感体验，也让学生感受数学成果来之不易和对数学家的崇敬之情。

从问题设置看，由易到难，梯度明显。由于是图像操作题，问题设置相对简单、直接，给与学生暗示操作方法，使学生有兴趣地了解教师提问，从而达到让学生由积极参与折纸活动向几何性质的学习和尺规作图原理的探索转变。

由于部分学生几何意识薄弱，主要原因在于双基落实过程中，深度不够。也就是说几何推理和操作的综合能力不到位，需要教师在教学过程中把握好难度分寸，给学生补充一些能激化思维、提升思维的内容，以达到对基本作图法的灵活应用。

数学折纸课教学有效避开数学抽象这一难点，选取与学生日常生活密切相连的情景，使思维能力“直观——抽象”自然转变。折纸课不仅让学生感受到数学的对称美，也让他们体验数学逻辑的严密性，从“直观几何”过渡到“证明几何”来验证数学是一门追求严谨的课程。

透过折纸学习尺规作图的，需要比一般学习方式多记忆折纸动作的转换，学生表示在思考尺规作图时，喜欢用折纸的方式思考，在尺规作图过程中，会很自然地联想到基本作图所对应的折纸动作，让学生多一种选择，乐趣。

参考文献：

[1]顾泠沅.《教学任务变革》.载《教育发展研究》，2001年第10期.

[2]张安军.《发现数学之美》.东北师范大学出版社，2013年5月.