橡胶隔振器的静态性能设计方法
2016-11-19成佳丽
成佳丽

摘 要:橡胶隔振器的静态性能对于橡胶隔振器的整体性能非常重要,为了使得橡胶隔振器性能得以改善,需要注重其静态性能的设计。其中影响橡胶隔震器性能的因素有很多,例如材料特点、结构、形状等等。该文首先采用双参数Mooney-Rivlin模型对橡胶隔振器静态性能进行数值计算。然后对隔振器开展了试验研究,并将两者进行对比,结果表明数值计算是可以为隔振器橡胶材料的设计选择提供一定依据的。该文研究的结果对隔振器的优化设计具有指导性意义。
关键词:隔振器 数值计算 Mooney-Rivlin模型
中图分类号:TB535.1 文献标识码:A 文章编号:1674-098X(2016)02(a)-0050-03
橡胶隔振器具有体积小、外型简单、有效吸收振动能量、成本低等诸多优点,目前已经在各种航空、航天、船舶等产品中广泛采用。该文研究的隔振器是为飞机高速转子动力装置安装系统设计的,外部金属壳体与动力装置、飞机机身刚性连接,内部橡胶通过粘结剂与外部金属壳体连成整体。一方面悬挂支撑动力装置,另一方面能够隔离飞机与动力装置之间的振动传递。这就要求该隔振器除了隔离振动之外,还要具备足够强度连接支撑100多公斤的动力装置,且在承受额定载荷、过载等各种情况下位移量不超过一定限制,否则将引起动力装置某些硬连接管路的变形或者断裂,造成更大危害。
隔振器的静态及动态特性由橡胶材料确定,工作性能与其材料特点、结构、形状、尺寸、承载的方式均有关系。该文研究的隔振器的弹性元件是硅橡胶,为一种典型的超弹材料,具有良好的伸缩性和复原性。但不同于金属材料的性能只需要较少参数表征而言,硅橡胶材料的特性表述非常错综复杂,且具有很强的非线性,如应变量大、应力应变呈高度非线性、材料近似不可压缩等。这使得在工程上对橡胶材料的运用存在非常大的不可预估性,长期以来多凭借经验或试凑法,通过不断反复试制、试验来设计满足性能要求的隔振器产品。
1 原理及算法模型
橡胶模型的数值计算基于超弹性理论,即基于橡胶各向同性和体积近似不可压缩的假设,用一个统一的物理量应变能密度函数()对橡胶进行表征。考虑到有限可压缩情况,橡胶材料模型最一般的形式如下:
ANSYS软件中双参数Mooney-Rivlin模型可以很好模拟橡胶材料的中、小型变形行为,与拉伸试验数据在100%、压缩50%应变范围内的相关性能较好。因此该文选择双参数Mooney-Rivlin模型进行橡胶件的有限元分析。其双参数应变能密度函数模型如下:
式(2)中,N、Cij和为材料常数,由材料试验所确定;对于不可压缩材料,J=1。
在计算过程中,通过确定其Mooney-Rivlin常数来表征其材料特性。利用Mooney-Rivlin常数,可以通过有限元方法计算出各种形状橡胶体的静态特性。
该文通过对橡胶材料采用单轴向拉伸试验得出Mooney-Rivlin模型中C10和C01常数。
对于单轴向拉伸,有(另外两个方向上的形变量)。
根据橡胶试片的单轴拉伸试验测试出不同拉伸比下的应力值,然后以为横坐标,以为纵坐标,把试验点表述在相应坐标系中,并把这些试验点回归成一条直线,C10为这条直线的截距,C01为这条直线的斜率。
2 数值计算
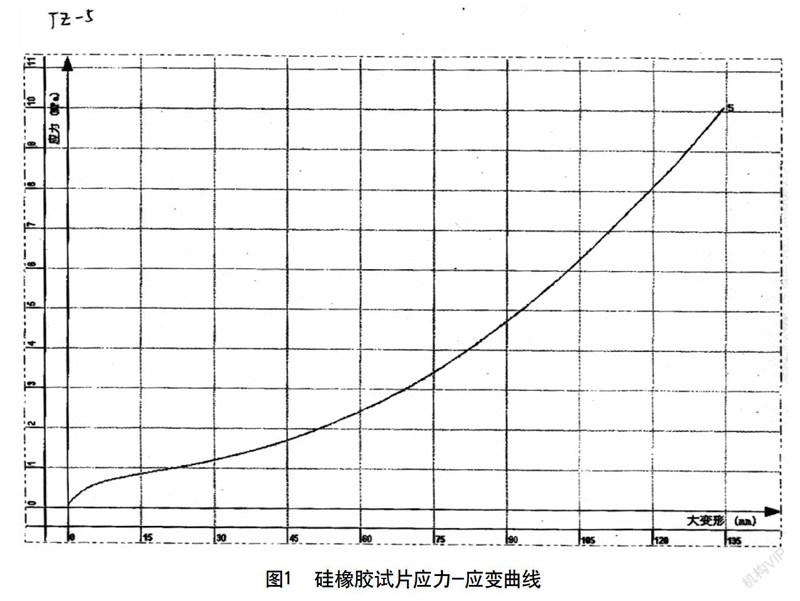
首先通过对不同弹性元件材料——橡胶的哑铃状试片分别进行单轴拉伸试验,得到相应的应力-应变曲线(注:试样制作标准按GB/T528-1998),从而获得其材料基本常数。再通过ANSYS软件对隔振器模型进行参数设置和分析,能够更加快速的选择满足或接近静态性能要求的橡胶材料。
如图1所示,为最终确认选择的硅橡胶材料的应力应变曲线。通过第一节提供的计算方法得到双参数Mooney-Rivlin常数,C10=0.228,C01=0.057。
隔振器的实体模型是利用Unigraphics建立的,将三维模型导入专业前处理软件ANSA作前处理,再利用ANSYS软件的Mooney-Rivlin模型对其橡胶件进行静态性能分析。
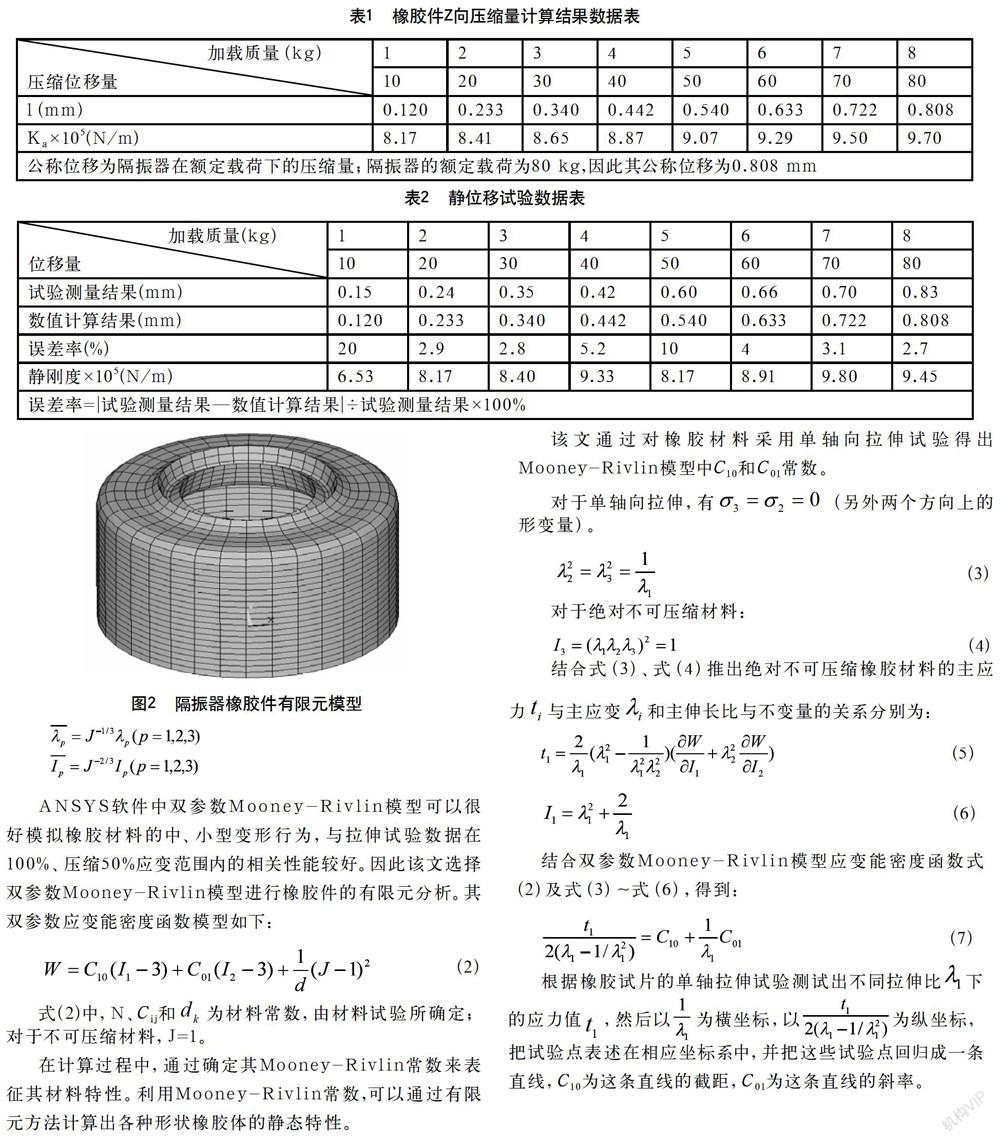
将隔振器中的橡胶件建立有限元模型,如图2所示。模型共包含4 356个六面体单元,单元类型为AYSYS软件中的SOLID185实体单元。
按照实际受力情况为模型设置边界条件,并在隔振器受力点上分别施加10~80 kg的重力,求解在10~80 kg(每10 kg为一个数值计算点)作用下内部平台的位移量,计算结果见表1及图3。
3 试验方法
在隔振器静力试验台上进行静态试验,测量隔振器不同载荷下的橡胶位移量。
试验设备及精度:静力试验台、BK-2B力传感器(0.05%)、DA-10位移传感器(0.5%)、液压缸,传感器测点布置如图4所示。
试验步骤:(1)将隔振器通过螺栓机械连接到静力试验台上;(2)调整液压缸操作泵,使力传感器调整到度数为零位置,保证试验开始前隔振器不受力,并读出此时位移传感器的读数L1;(3)通过液压缸对隔振器分别施加10~80 kg(每10 kg递增)的拉力,保持3 s后,记下位移传感器仪表稳定后的读数L2;(4)隔振器在每个拉力下的压缩位移为L=L2- L1,该拉力下隔振器的静强度N/m。
4 试验与计算结果对比
将试验结果与数值模拟结果进行对比分析,计算其误差率得到结果如表2。
5 结语
对比隔振器静态试验测量结果,可以看到数值计算结果具有较好的符合性。证明Mooney-Rivlin模型的数值计算结果对今后设计隔振器静态性能以及确定橡胶材料的选择是一种有效的途径。采用数值计算的方法对橡胶隔振器进行静态性能分析,不仅能够在初期检验产品设计的合理性,还能够安全、有效地代替部分试验,大大减少研制前期对橡胶材料的繁琐试制和试验工作、缩短研发周期。
参考文献
[1] 朱石坚,楼京俊,何其伟,等.振动理论与隔振技术[M].北京:国防工业出版社,2006.
[2] Brennant M.J.,Garcia-Bonito J.,Elliott S.J.,et al.Experimental Investigation of Different Actuator Technologies for Active Vibration Control[J].Sm-art Mater.Struct,1999(8):145-153.
[3] 杨晓翔.非线性橡胶材料的有限单元法[M].北京:石油工业出版社,1999:70-82.
[4] Xun Li,Ben S.Cazzolato,Colin H.Hansen.Active Vibr-ation isolation of diesel engines in ships[D].Ninth Internati-onal Congress on Sound and Vibration,ICSV9.
[5] 昊铭.小尺寸橡胶隔振器的设计及试验研究[D].武汉:华中科技大学,2004.
[6] 易太连,翁雪涛,朱石坚.不可压缩橡胶体的静态性能分析[J].海军工程大学学报,2002,14(2):76-80.
