基于优化钻石模型的产业竞争力评估方法

2016-11-19刘宇杨志萍王春明杜倩戈勤

现代情报 2016年4期

刘宇　杨志萍　王春明　杜倩　戈勤

〔摘要〕[目的/意义]构建一套有效的产业竞争力评价体系指标及模型，为我国各地区的产业发展水平和结构稳定度的分析、评价和优化提供支撑。[方法/过程]在总结国内外产业竞争力研究的基础上，运用“信息熵”和“粗糙集”的理论方法，对“钻石模型”进行优化，建立起一套体系化的产业竞争力评价指标模型。以我国机械工业2012年的数据为实证研究对象，运用该模型分析评价我国各省级地区机械工业的竞争发展地位和结构稳定度。[结果/结论]本文构建的一套基于优化钻石模型的产业竞争力评价模型具有可适性和有效性，运用于我国机械工业的评价结果与各地区的实际运行情况基本相符。

〔关键词〕产业竞争力；钻石模型；粗糙集；机械工业；信息熵

DOI：10.3969/j.issn.1008-0821.2016.04.012

〔中图分类号〕G250.25 〔文献标识码〕A 〔文章编号〕1008-0821（2016）04-0062-08

〔Abstract〕[Purpose/significance]This paper is aimed at establishing an effective index system and model of industrial competitiveness evaluation，in order to help analyze，evaluate and optimize industrial development level and structure stability of Chinas provincial regions.[Method/process]On the basis of summarizing the previous studies of industrial competitiveness in China and abroad，this paper uses“Information Entropy”and“Rough Sets”theoretical method to optimize the“Michael Porter Diamond Model”，further more to establish a set of systematic index model of industrial competitiveness evaluation.This model is used to analyze and evaluate the development status and structure stability of machinery industry of Chinas provincial regions，while the industrial data of machinery industry in 2012 is as the empirical research object.[Result/conclusion]This systematic index model of industrial competitiveness evaluation is applicative and effective； the evaluation result of Chinas machinery industry running out via this model is closely matched with the actual operation of these regions.

〔Key words〕industrial competitiveness；diamond model；rough sets；machinery industry；information entropy

随着信息技术的突飞猛进和全球经济一体化程度的不断加快，使得国家或地区之间的产业竞争越发激烈。产业竞争力的研究，能够反映出某国家或地区的某一特定产业相对于他国或地区同一产业在生产效率、满足市场需求、持续获利等方面所体现的竞争能力，因此近年来世界各国对其的研究需求也越发强烈。对于我国而言，自21世纪以来的经济跨越式发展带来了巨大的社会财富，同时这种粗放式的爆发增长带来的竞争压力也在不断的增加。许多学者开始思考如何进行产业竞争力的评价、梳理和升级，使得资源配置更为优化，经济发展更具有可持续性。对于我国的高校和科研院所而言，越来越多的科研机构对于产业化信息越发地重视，试图通过一系列的产业竞争力评价和分析，找到更适宜的产、学、研结合的可持续性发展路线，从而使其科研成果更优化地产生社会效益。从各层面而言，对于产业竞争力的研究需求迫切，探索一套适宜的产业竞争力评估方法、评价指标体系和研究模型具有较高的理论价值和实用意义。

机械工业也称“机器制造工业”，指的是制造机械产品的工业领域，包括冶金设备、化工设备、动力设备、农业设备、矿山设备等等的制造，为工农生产、交通运输和国防军事等提供生产手段和装置设备，是整个国民经济和国防现代化的重要基础。机械工业的发展水平是衡量一个国家或地区工业化程度的重要标志之一。因此，本文拟通过建立的产业竞争力评价模型，对我国各地区机械工业的现实数据进行实证分析，检验模型的可行性和有效性。

1 理论基础与分析

1.1 钻石模型及其衍生发展

产业竞争力的概念是多角度、多层次和动态的，其研究的代表性人物美国哈佛商学院战略管理学家迈克尔·波特于1997年在《Competitive Advantage》一书中将产业竞争力定义为：一个国家能否创造一个良好的商业环境，使该国企业获得竞争优势的能力。目前，对于产业竞争力较为广泛的认识是：指某国或某一地区的某个特定产业相对于他国或地区同一产业在生产效率、满足市场需求、持续获利等方面所体现的竞争能力。

产业竞争力理论可以溯源至1817年大卫·李嘉图的比较优势理论，经由埃利·赫克歇尔、贝蒂尔·俄林、熊彼特、筱原三代平和保罗·克格鲁曼等人不断优化发展，相继产生了动态比较费用学说、技术创新理论和战略贸易理论，直至发展出了竞争优势理论，逐渐开始尝试对产业竞争力进行要素驱动、投资驱动、创新驱动、财富驱动等4个层次的阶段定性，以及生产要素、市场需求、相关支持产业、企业战略等6个因素的量化评价。1990年，普拉海拉德和海默发表《企业的核心竞争力》一文，提出了核心竞争力理论，有效地补充了竞争优势理论。同年，迈克尔·波特提出了著名的钻石模型（又称波特菱形理论，Michael Porter Diamond Model），用于分析一个国家的某一产业如何形成整体优势。该模型认为，产业竞争力是由生产要素，国内市场需求，相关与支持性产业，企业战略、企业结构和同业竞争等4个主要因素，以及政府行为、机遇等两个辅助因素共同作用而形成的。其中，前4个因素是产业竞争力的主要影响因素，构成“钻石模型”的主体框架[1]。

此后，国内外相继有不少专家提出了一些批评和优化改良意见。1992年，英国学者邓宁认为“跨国商务活动”应该与机遇和政府作为同等变量考量，据此对钻石模型进行修正，提出了“国际化钻石模型”[2]。鲁格曼和克鲁兹在分析加拿大国家竞争优势时提出了“双钻石模型”[3]。其后韩国汉城大学教授赵东成根据波特的钻石模型，结合韩国的实际，提出了国际竞争力的“九因素模型”。他认为，新模型应符合以下两个目标要求：一是更好地评估创造发展中国家国际竞争力的因素；二是说明一国如何增强其国家优势[4]。

我国的金培等人指出波特的钻石模型分析范式针对我国实际情况存在一定的缺陷，尤其是对于不同经济发展阶段，该分析范式不应该是一成不变的。继而，他提出了“国际竞争力分析框架”。金培认为，各国产业在世界经济体系中的地位是由多种因素所共同决定的，从国际分工来看，比较优势具有决定性作用；从产业竞争的角度来看，竞争优势起着决定性的作用；即比较优势和竞争优势共同决定了各国产业的国际地位及其变化趋势[5]。2006年，复旦大学的芮明杰引入了“知识吸收与创新能力”，提出了“新钻石模型”。他认为将“知识吸收与创新能力”作为核心能够真正发展产业的持续性竞争力[6]。2012年，方慧等人将“产业发展阶段”融入钻石模型，提出了“动态钻石模型”，并将其运用于到文化贸易竞争力的分析和实证研究中[7]。2014年，何伟基于旅游文化产业融合的理念，构建了“融合双钻石模型”，分析西藏文化产业的竞争优势[8]。

除了理论模型探讨之外，我国许多科研和政府机构也开始针对某一地域或者某一行业尝试开展产业竞争力的实例研究。例如，大连理工大学宿倩对城市旅游产业的竞争力研究[9]；苏州大学李丹丹基于因子分析法的服务外包产业竞争力评价研究[10]；沈阳大学经济学院高秀艳等人以辽宁省为例，开展的区域高技术竞争力评价与对策分析[11]；中南大学黄志勇基于R-SCP分析的我国中药产业竞争力[12]；四川大学李菁等人以甘肃陇南花椒产业为例开展的农业产业集群模式体系研究[13]；中国人民大学丁嘉伦开展的中国旅游服务贸易竞争力分析研究[14]；浙江财经大学林娟娟基于“新钻石模型”分析的“银发产业”发展[15]；四川大学张令伟针对高校的艺术学学科竞争力开展了综合评价[16]，等等。

目前的产业竞争力研究热度较高，每年均有大量的文献产出，但是，实质性的理论突破却趋于停滞。由于产业竞争力的内涵及决定因素存在较大的差异，其评价标准及指标体系也一直未能形成一个各方都认可的标准化共识，从而限制了产业竞争力评价体系对于国家或地区竞争力提升的重要作用。不仅如此，具体到我国的产业竞争力研究而言，由于国情造成的政治、经济环境差异，“钻石模型”及其衍生的理论模型的评价指标，仍需要进一步优化改进，尽力消除评价过程中的主观性和不确定性，才能形成更适宜、更具价值的产业竞争力评估方法。

1.2 粗糙集理论

“粗糙集（Rough Set）”是一种数学方法，能有效地处理模糊或不完整的信息，揭示数据的内在规律与隐含知识[17]。最早可以溯源至1965年的“模糊理论（Fuzzy Logic）”，当时不少理论计算机科学家和逻辑学家试图找到某种方法来解决G.Frege的信息含糊概念，他们采用了隶属函数来处理信息的模糊性，称之为“模糊法”，但是依然具有相当的主观性。1982年，波兰学者Pawlak提出了“粗糙集”理论，将边界线区域思想用确定的数学公式加以描述，由事实数据来决定，从“模糊理论”中剥离出了更具有客观性的粗糙集理论[18]。

作为知识（或信息）的约简方法，粗糙集是一种处理不精确、不确定和不完全数据的新的理论工具，是在保留基本知识（或信息），同时保证对象的分类能力不变的基础上，消除重复、冗余的属性和属性值，实现对知识的压缩和再提炼。它可以通过对数据的分析和推理来发现隐含的知识、揭示潜在的规律。在粗糙集理论中，知识（或信息）被认为是一种分类能力。其核心是利用等价关系来对对象集合进行划分。其最主要的特点在于：“粗糙集”无需提供对知识或数据的主观评价，仅根据观测数据就能达到删除冗余信息，比较不完备知识的程度-粗糙度，界定属性间的依赖性和重要性的目的。因此，我们将“粗糙集”方法引入钻石模型为基础的产业竞争力指标体系的优化中，以增强竞争力评价的客观性、合理性和有效性。

1.3 信息熵理论

熵的概念源自热物理学，指的是热能除以温度所得的商，标志着热量转化为功的程度，意义在于对动力学层面不能做功的能量进行总测度，从而成为可以表达分子状态杂乱程度的物理量[19]。信息论的鼻祖之一C.E.Shannon借鉴此概念，将其引入了信息理论，作为某种特定信息出现的离散随机事件概率的度量，从而可以用来衡量信息价值高低。一个信息系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。由此，将信息熵用作信息系统有序化程度的一种度量。

信息熵的度量旨在衡量数据源的平均不定度。在信息论中信息源输出的是随机量，因而其不定度可以用概率分布来度量。例如，记H（X）=H（P1，P2，…，Pn）=P（xi）logP（xi），这里P（xi），i=1，2，…，n为信源取第i个符号的概率。P（xi）=1，H（X）称为该信息源的信息熵[20]。

由于钻石模型指标体系具有一定的定性概念，其变量呈现一定的连续属性。而“粗糙集”理论的应用在处理定性概念和连续数据时，存在一定的缺陷，人为控制因素过多将难以保证指标体系优化的质量。因此，本文采用信息熵理论使指标体系的类别更加标准客观化，同时结合“粗糙集”的模糊聚类思想，以指标体系的属性度作为信息熵计算的基础，综合确定指标体系的数量。

2 基于优化钻石模型的产业竞争力评价模型构建

2.1 评价指标体系的设计

按照数据处理的系统性和科学性等原则，秉性“先全面着手、再化繁为简”的方针，将产业竞争力评价指标体系分为“目标层”、“准则层”、“子准则层”和“指标层”4个层次。其中，准则层包括6个维度：资本竞争力、生产竞争力、市场竞争力、技术竞争力、成长竞争力和管理竞争力，即为原钻石模型6个维度的具体表征。同时，再对准则层进行进一步细化，使每个准则层产生2～3个子准则，再对子准则层进行深度的指标阐释，让每个子准则层下属形成2～7个具体的可操作性指标，共计43个指标组成。如表1所示。

2.2 评价模型

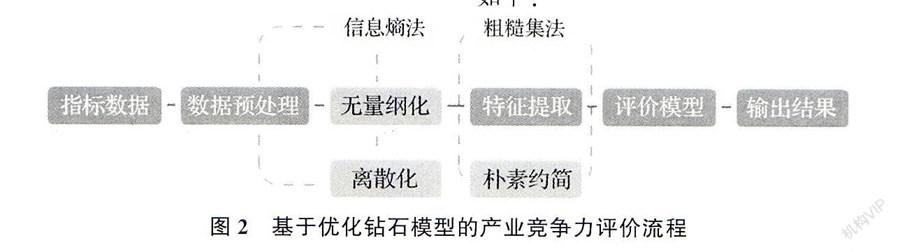
对机械工业进行竞争力评价的时候，由于数据指标具有线性和量纲性，使得同类和不同类的数据之间都难以具有清晰的可对比性。信息熵法的数据有序性，适用于指标识别和数据分类，再结合无量纲化处理，使得各指标具有更为明显的属性度。当然，仅如此是不够的，因为无法对指标数据进行维数简化，不能识别和删减系统中相似指标所产生的数据噪音，冗杂的指标体系将造成效率低下。而粗糙集在处理该类问题时具有很大的作用，可以通过属性的朴素约简进行有效的降维处理。因此，我们首先通过信息熵法对数据进行预处理，使得数据无量纲化和离散化，再基于粗糙集法对指标体系进行朴素约简和降维处理，提取出特征属性指标，从而进行产业竞争力评价，其过程如图2所示。

3 我国机械工业实证分析

3.1 数据来源

本文数据取自《中国机械工业年鉴》和Wind资讯产业数据库，不含我国西藏自治区及港澳台地区数据。时间窗口成长性指标数据取自2011年和2012年2年外，其他指标数据均取自2012年。

3.2 评价过程

3.2.1 数据预处理

将采集来的基础数据进行归并和整理，前期处理包括3项内容：其一，不同来源的数据进行比对核实；其二，同一指标数据的单位统一化处理；其三，个别缺失较严重的数据进行同类别替代。其后，为了克服不同指标数据的量纲不同，导致的无法对比分析，通过极大极小法对数据进行无量纲化处理，消除原始变量的量纲影响[21]。运算式如下：

3.2.2 指标属性约简

运用挪威科技大学研发的粗糙集软件Rosetta表格逻辑数据分析工具来进行处理，并在此基础上进行属性指标约简。其主要内容为两个部分：其一，对初选指标体系存在的不确定性因素，包含的不精确或不完整的噪音，进行明确和除噪；其二，对内容相关性过高的指标，将会影响准则层的属性，对初选指标体系进行合理优化去冗。

通过选择朴素贝叶斯离散和遗传约简的处理方法，我们以最大概率指标替代该准则，最后得出“企业数（家）”、“工业销售产值（当年价）”、“资产总额”、“资产负债比重”、“固定资产新度系数”和“利润总额”六大指标作为最优属性特征变量。

3.2.3 指标权重系数

为了得到更为准确的权重系数，针对属性约简后的“六大指标”，综合“层次分析法”和“德尔菲（Delphi）法”来进行确定。具体实施流程为：（1）专家咨询；（2）一致性首次检验；（3）判断计算权重；（4）一致性二次检验；（5）确定权重系数。

3.2.4 结构稳定程度

由于六大指标数据的测量尺度不同，指标的离散程度也差异较大，我们引入变异系数（Coefficient of Variation，简称CV）来衡量产业竞争力的结构稳定性。变异系数是标准差（Standard Deviation，简称SD）与算术平均数（Arithmetic Average，简称AA）的比值，不具有量纲，反映了数据离散程度的绝对值，因此可以消除综合指标体系对两个或多个资料变异程度比较的影响，从而衡量产业竞争力的结构强度[22]。

SDr=∑nr=1[Xr-AA（Xr）]n （Xr为原数据）

CVr=[（SDr÷AA（Xr）]×100%

3.3 评价结果

运用以上基于优化钻石模型的产业竞争力评价指标体系及方法，对我国各地区（省/市/自治区）的机械工业进行总体评价的结果见表2。

从表2中可以看出，我国各地区（省/市/区）机械工业的竞争力综合排名中，江苏省得分为0.988分，在各维度指标中均有良好表现，以远超第二名的突出优势排名第一。

其后的山东、浙江、广东和上海在机械工业领域也具有很强的竞争力，综合得分名列2～5位，得分均在0.4分以上，属于第一梯队。这些地区的竞争力分维度均处于全国前列，例如，山东的工业销售产值和利润总额较为突出，浙江的企业数和固定资产新度系数较突出，单项指标得分均在0.7分以上。其次，辽宁、河南、湖北、河北、安徽、湖南、北京和四川等省市，综合得分处于0.2～0.4之间，属于第二梯队。这些地区的机械工业竞争力相对较强，并在个别单项指标上具有较强实力。例如，河南、河北、安徽、湖南和北京5省市的固定资产新度系数分值均在0.7分以上，其中湖南省更是高达0.92分，说明这些地区的机械工业设备更新步伐较快或者新增升级设备较多，也反映出这些地区的机械工业发展活跃度较高。

再次，天津、吉林、重庆、福建、广西、江西和陕西等地区，产业竞争力得分值处于0.1～0.2分之间，综合得分相对较低，属于第三梯队。这些地区的机械工业发展具有一定的潜在发展实力，但在个别指标维度上处在全国前列，但其他指标维度的较大劣势造成整体排名较低，需要有针对性的弥补其劣势。最后，山西、新疆、黑龙江、青海、宁夏、贵州、内蒙古、海南、云南和甘肃10省市区的产业竞争力综合得分在0.1分以下；同时，由于其他指标维度均处于低水平（0.1分以下），单个的固定资产新度系数较高，只能反映出新增设备上的一定发展，这些地区的机械工业整体处于较低水平。

综合来看，江苏、山东、浙江、广东和上海等省市的机械工业竞争力处于优势地位，引领着整个产业的发展；尤其是江苏省以绝对优势领跑全国，是机械工业领域当之无愧的全国发展领头羊。这些地区均为沿海经济发达地区，有丰富的市场需求和先进的科技水平，并拥有全国领先的港口货运和外贸优势，机械工业发展的基础厚、平台高，具有绝对的优势。除北京、天津、重庆等直辖市由于自身体量远小于省份地区，造成整体排名不够突出，其他处于第二、三梯队的地区多为中部省份，比如河南、河北、湖北、湖南、安徽、江西等多个省市，以及辽宁、吉林等原重工业区域，这些地区的竞争力是机械工业全国布局发展的中间力量，其竞争实力虽然较之沿海发达地区有差距，但是随着传统产业的由东向西转移发展的大趋势，以及国家大力推行的西部大开发、中部崛起和重振东北老工业区的战略，这些地区若能弥补劣势，协调各要素之间的不平衡性，无疑会将巨大的发展潜力转化为现实的产业实力。以甘肃、青海、贵州等省为代表的西部地区，在机械工业领域的竞争力较弱，各维度方向仍需全面的加强发展，企盼能够抓住沿海城市产业转型和西部大开发的战略，深度拓展自身的发展潜力，促进机械工业的发展迈向新台阶。

由于变异系数反映出了产业竞争力各维度指标的均衡发展程度，我们从表3可以看出，广东、山东、江苏、辽宁、上海和浙江等6省市依然排名前列，说明这些地区的机械工业不仅具有较强的综合产业竞争力，并且其竞争力的结构强度也较好。此外，湖北、吉林等12省市的变异系数分值也在1.0以下，其产业竞争力指标发展较为均衡，产业结构基本具有一定的稳定性；而青海、新疆等省市或自治区，变异系数超过了2.0，说明其产业竞争力结构强度较弱，产业发展具有不均衡性。

为了探讨我国各地区（省/市/区）机械工业领域的产业竞争力与变异系数之间的关系，我们以各地区竞争力分值为纵轴，以各地区的产业竞争力变异系数值为横轴，得到如图3所示的关系图。

江苏省具有十分领先的产业竞争力，并且其变异系数也控制在相对很低的状态，各竞争力要素间的结构稳定性较好，综合实力非常强，在未来的发展前景也将持续稳定和领先。山东、浙江、广东、上海和辽宁等省市也具有较强的竞争力得分，和较低的变异系数分值，未来的发展前景看好，属于持续领先的地区。反之，青海、新疆、贵州、云南等地区，不仅竞争力得分低，其变异系数分值也非常高，竞争力结构稳定性较为缺乏，这说明了两点：其一，机械工业基础弱，整体竞争力水平较低；其二，个别维度指标具有较高的水平，具备一定的发展潜力，当然也不排除其原先较低的体量，在同等变量增长的情况下导致发展比率较高，而引起个别维度指标激增。而甘肃省则是较为特殊的一个，其竞争力得分在30个省级地区中排名最低，但同时又具有较低的变异系数分值，说明该地区的机械工业发展前景有待进一步提升。

总体来看，我国机械工业领域的产业竞争力得分与变异系数之间呈线一条较明显的负相关趋势曲线，竞争力强的地区其结构稳定性也较高，说明各地区在提升机械工业竞争力的过程中，大都较为注重产业各维度之间的均衡发展。

4 结论

本文在总结钻石模型及其衍生体系的基础上，引入“信息熵理论”和“粗糙集”的理论方法，优化了“钻石模型”理论的产业竞争力评价指标，建立起一套体系化的产业竞争力研究评价模型。与传统分析模型相比，该模型强调了资源禀赋在竞争力构成中的重要作用，并有效解决了原钻石模型中属性指标的含糊、冗杂和噪音问题，实现了在不改变指标体系的属性指代能力的前提下进行知识约简的能力。运用此优化钻石模型，对我国2012年机械工业领域进行了实证研究，分析我国机械工业领域的竞争力格局，以及产业竞争力各维度指标之间的结构稳定程度，评价我国不同地区机械工业领域的市场地位。评价结果与我国各地区机械行业的实际运行情况基本相符，能够反映出各地区的机械产业竞争力现状及发展趋势。

参考文献

[1]迈克尔·波特.国家竞争优势[M].李明轩，译.北京：中信出版社，2007.

[2]Dunning，J H.The Competitive Advantage of Countries and the Activities of Transnational Corporations[J].Transnational Corporations，1992，（1）.

[3]Alan M R，Joseph R D.“The Double Diamond Model”of International Competitiveness：The Canadian Experience[J].Management International Review，Second Quarter，1993，33（2）：17-39.

[4]Cho，D S.A dynamic approach to international competitiveness：The case of Korea[J].Journal of Far Eastern Business，1994，（1）.

[5]金碚，李钢，陈志.加入WTO以来中国制造业国际竞争力的实证分析[J].中国工业经济，2006，（10）：5-14.

[6]芮明杰.产业竞争力的“新钻石模型”[J].社会科学，2006，（4）：68-73.

[7]方慧，尚雅楠.基于动态钻石模型的中国文化贸易竞争力研究[J].世界经济研究，2012，（1）：44-50.

[8]何伟.基于“融合双钻石模型”的西藏文化产业竞争力分析[J].西藏大学学报，2014，（4）：41-47.

[9]宿倩.城市旅游产业竞争力研究[D].大连：大连理工大学，2004.

[10]李丹丹.基于因子分析法的服务外包产业竞争力评价研究——以中国服务外包示范城市为例[D].苏州：苏州大学，2012.

[11]高秀艳，高亢.区域高技术竞争力评价与对策分析——以辽宁省为例[J].企业经济，2012，（1）：141-143.

[12]黄志勇.基于R-SCP分析的我国中药产业竞争力提升研究[D].长沙：中南大学，2011.

[13]李菁，揭筱纹.基于钻石模型的农业产业集群模式体系研究——以甘肃陇南花椒产业为例[J].兰州大学学报，2014，（2）：121-126.

[14]丁嘉伦.基于钻石模型的中国旅游服务贸易竞争力分析[J].中国物价，2014，（12）：82-84.

[15]林娟娟.“银发产业”发展的“新钻石模型”分析[J].商，2015，17：283-284.