Fellenius 法的解析解法

李 闯，赵盛杰，董 晔，李鹏宇，穆孟婧

（1.华能澜沧江水电股份有限公司漫湾电厂，云南临沧675805；2.华北电力大学，北京102206）

Fellenius 法的解析解法

李 闯1，赵盛杰1，董 晔2，李鹏宇2，穆孟婧2

（1.华能澜沧江水电股份有限公司漫湾电厂，云南临沧675805；2.华北电力大学，北京102206）

Fellenius法是一种经典的边坡稳定性分析方法。由于此法更加安全，故而在工程施工中被广泛应用。现行方法多为数值计算方法，通过大量分条和滑弧的遍历来确定最小安全系数Ks和最危险滑弧的位置（圆心横坐标x0，圆心纵坐标y0，半径R）。但数值计算方法计算量浩大且精度不及解析计算方法。通过对Fellenius法的连加形式的数学模型进行分析，得到了Fellenius法积分形式的数学模型，进而得到了安全系数的表达式K（x0，y0，R）。然后，将求解最小安全系数Ks的问题转化为K（x0，y0，R）求极值问题，并导出了K（x0，y0，R）取最小值Ks的时候须满足的方程gradK=（0，0，0）。最后，基于gradK=（0，0，0）无根式解这一基本事实，利用麦克劳林展开将K（x0，y0，R）简化，并利用费拉里法对gradK=（0，0，0）进行解答，得到了最危险滑弧的位置（xs，ys，Rs）的表达式。将（xs，ys，Rs）代入K（x0，y0，R），得到了最小安全系数Ks=K（xs，ys，Rs）。继而，只需要得知土坡的相关参数，便可得到Ks，无需试算与解方程且具有较高的效率。

边坡稳定性；Fellenius法；解析解；超越方程

Fellenius法（Fellenius于1936年提出）是边坡稳定性分析的经典算法。虽然Fellenius法不满足土条静力平衡条件，但此法应用的时间很长，积累了丰富的工程经验。而且一般得到的安全系数偏低，偏于安全［1-2］，是工程上常用的方法，而且列入《碾压式土石坝设计规范》［3］（SL274-2001）。很早人们就意识到确定具有最小安全系数的边坡问题是一优化问题［4-6］，多年来，发展出许多计算安全系数的方法。文献中出现质量很高的评论综述［7-11］。

早期的解法有变分法［12-13］、固定模式搜索法［14-15］、数学规划方法［16-21］，动态规划法［22-24］、随机搜索方法（如Monte Carlo法）［25-28］等，近年发展了一些被公认为全局搜索能力强、搜索效率高的智能算法。如将模拟退火［30］、遗传算法［31］，蚁群算法［33］，粒子群算法［34-35］等方法用于求解边坡全局最小安全系数。

以上基于条分的方法，或者因初值选择不当，计算可能不收敛，或只能获得局部极小解，需要根据经验做出判断，或者采用智能算法得到全局最小解，但工作量较大。近年有人针对Fellenius法，试图获得解析解表达式。实质是采用积分算式代替条块的代数求和，但仍然采用试算方法和最优化方法来确定边坡的最危险滑弧和最小安全系数。张天宝［36］于1978年推导出均质土坡稳定系数是滑弧的圆心坐标和半径的多元函数，但只给出了数值解法。黄文东［37］1999年提出在连接滑弧两个端点的弦的中垂线上搜索最危险滑弧的圆心，该方法在一定程度上减少了搜索的工作量，但也有盲目性。对于解析解法，杨庚宇等［38］在1988年、Cao Jinggang等［39］在1999年提出了安全系数的解析算式，其本质便是用数学积分代替了简单的代数之和，但而后便是通过试算抑或最优化方法来计算最小安全系数，即二人皆未得到最小安全系数的解析算式。李同录等［40］于2004将地面线用分段直线方程表示，将滑动面用一圆弧方程表示，推导出了求解稳定系数的解析式。相较于张天宝的工作，李同录假定两点固定，将函数变为一元函数，通过对于一元函数的求导来确定该条件下的最小滑动面。蒋斌松等［41］2004年对于圆弧形滑裂面，采用解析方法，首先建立边坡安全系数的解析表达式，然后利用函数取极值的条件，通过迭代方法获得边坡临界滑裂面和最小安全系数。韩晓雷等［42］于2009年建立了边坡稳定性分析的平面直角坐标系，得到了该坐标系下的边坡稳定分析瑞典圆弧法的积分表达式。以简单均质黏性土坡为研究对象，结合MATLAB遗传算法工具箱，建立了基于瑞典圆弧法的遗传算法优化模型，实现了边坡稳定分析最小安全系数的自动寻优。张向东等［43］于2014年转化传统数学模型的连加为积分，对于异形边坡进行了简化，得到了其广义数学模型。

以上工作虽将条分形式表达为数学积分形式，但都未获得直接的结果表达，仍需通过试算或最优化方法来计算最小安全系数，即皆未得到最小安全系数的解析算式。本文根据严格的数学推导，得到了安全系数K的解析算式，其为滑弧的圆心坐标（x0，y0）及半径R的函数K=K（x0，y0，R）。根据三元函数取极值的条件，导出K函数取极值的时候应满足的方程组：gradK=（0，0，0），但gradK=（0，0，0）包含根号，在求导过程中出现了高于5次幂的项，根据文献［44］的Galois理论，五次以上之方程式没有根式解，而四次以下有根式解。即，gradK=（0，0，0）不存在根式解。故而，对K（x0，y0，R）中的根号进行麦克劳林二阶展开，在截去高阶项后得到了函数K的一个相对简单的表达式。然后，利用费拉里法［45］，求解出了gradK=（0，0，0）的解（xs，ys，Rs），将（xs，ys，Rs）代入到K（x0，y0，R）中，进而得到最小安全系数Ks=K（xs，ys，Rs）。

1 安全系数的解析解

Fellenius法不考虑土条间的作用力，将边坡问题界定为平面应变问题。图1中，坡高为H；点O是坐标系原点，坡脚在其右上方处，水平距离为1.5H，竖直距离为是滑弧的圆心，R为滑弧的半径；α为坡角；区域D坡底、坡面和坡顶与滑弧所围城区域；黑色条带部分为土条；i是土条的编号；θi是第i号土条的底面中点的法线与铅垂线的夹角，若θi位于铅垂线的左边则为负；若θi位于铅垂线的右边则为正。

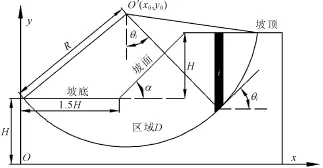
图1 坡体模型计算坐标系的建立

根据Fellenius法，土坡的安全系数计算如下

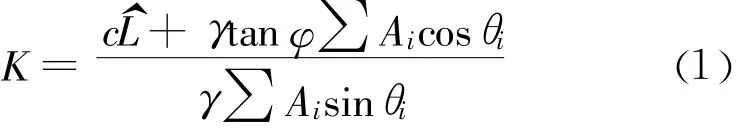
式中：K是安全系数，c、φ、γ分别是土的黏聚力、内摩擦角、重度，＾L是滑弧的长度，Ai是第i号土条的面积。式（1）是传统的数学模型，仅仅是一个比较粗略的数学模型，而且计算较复杂。基于几何关系和积分知识对式（1）进行积分转化。

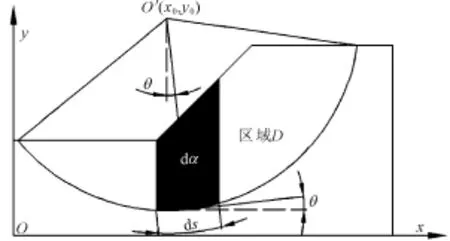
图2 土坡微分示意图

图2中，dσ为微分单元（为方便辨识，故意将图2中的微分单元dσ扩大），θ是dσ的底面中点的法线与竖直线的夹角。由此，式（1）的积分形式为

图2中，滑弧的方程为

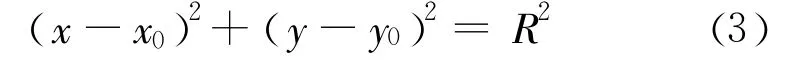
联系图2，我们可以得出，θ的正切即滑弧的斜率，数学表达式为

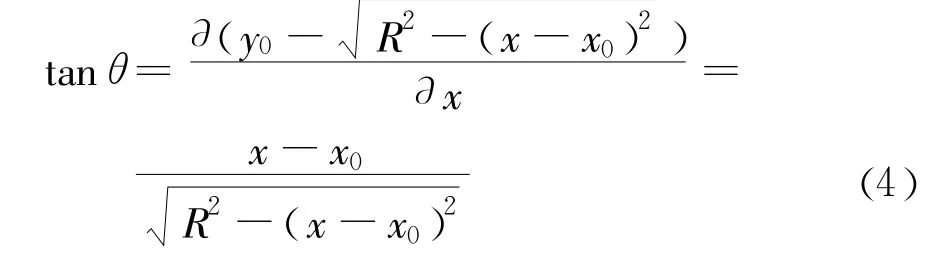
根据式（4），得到θ的正弦和余弦，

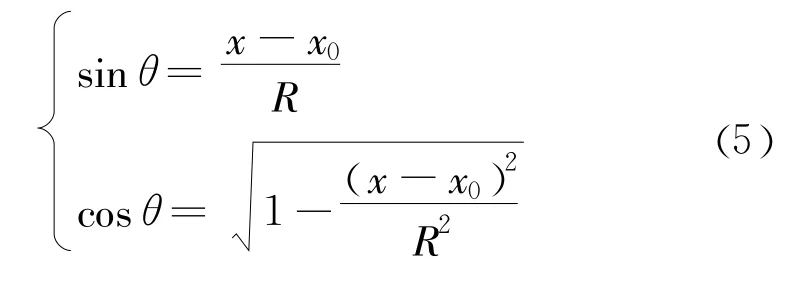
在此，需要讨论θ的取值。根据式（4），若x＜x0，θ为负；若x=x0，θ为0；若x＞x0，θ为正。此外，考虑一些极端情况，当y0≤2H的时候（实际工程中基本不存在），θ可以取到π/2。当θ=π/2的时候，即y= y0，所对应的微分单元的面积也是0。这样一来，对于最终求解安全系数便没有影响。

图3 土坡微分变换示意图

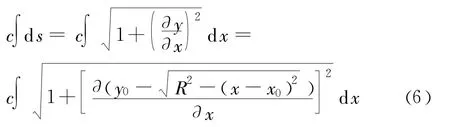
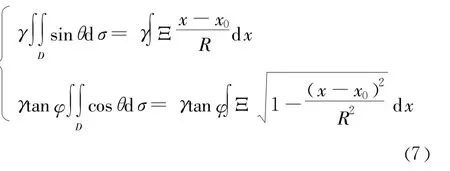
式（7）中，

式（8）中，f（x）是坡底、坡面、坡顶的函数

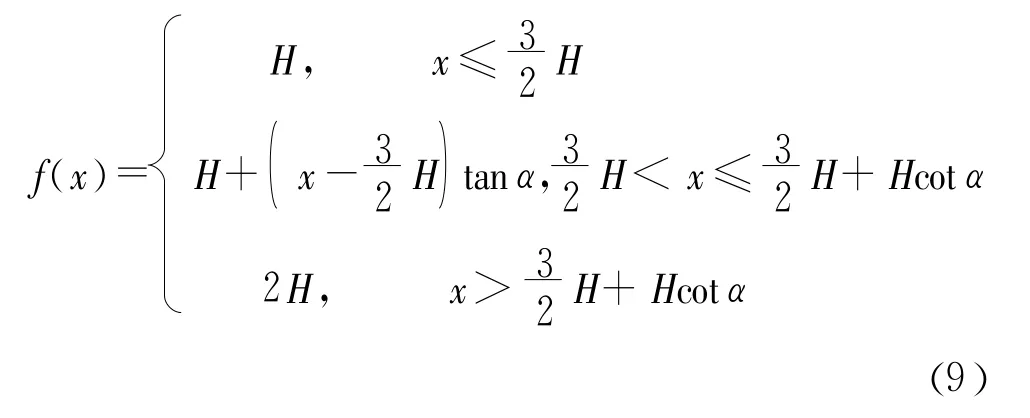
将式（6）和式（7）代入式（2），便可以得到K的表达式

式（10）中，

式（11）的四个角θ1、θ2、θ11、θ21的几何意义如图4所示，

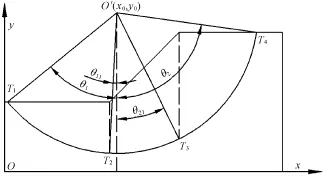
图4 θ1、θ2、θ11、θ21的几何意义

图4中，坡底与滑弧的交点为T1；从坡脚向下作垂线，与滑弧的交点为T2；从坡面和坡顶的交点向下作垂线，与滑弧的交点为T3；坡顶与滑弧的交点为T4。线段与铅垂线的夹角为θ1；线段与铅垂线的夹角为θ11；线段与铅垂线的夹角为θ21；线段与铅垂线的夹角为θ2。根据图4，θ1＜ θ2、θ11＜θ2、θ21＜θ2，而θ2＜π/2。

至此，建立了安全系数K与滑弧位置的函数关系，K=K（x0，y0，R）。在此需要注意的是，安全系数K并非图1、图2、图3中x与y的函数。为便于理解，可设想一个四维空间，这个四维空间的元素为K、x0、y0、R，则K=K（x0，y0，R）是这个四维空间的三维流型。

2 滑弧的圆心坐标和半径的求解

根据三元函数取极值的条件，导出K（x0，y0，R）取极值的时候应满足的方程

式（12）的解为（xs，ys，Rs），则最小安全系数便为Ks=K（xs，ys，Rs）。式（12）是一个极端复杂的方程式。式（12）中包含了许多根式项和三角函数，在求导的过程中出现了高于5次幂的项。根据文献［44］的Galois理论，五次以上之方程式没有根式解，而四次以下有根式解，故而，式（12）不存在根式解。但是，对K函数表达式中的根号进行麦克劳林二阶展开，在截去高阶项后便能得到函数K的一个相对简单的表达式。对于被替换后的函数K，进行求导等相关操作的时候，便不会出现5次幂的项或者高于5次幂的项。对于最高次幂为四次幂的参数的求解，可首先将其整理成一元四次方程的普遍形式，然后利用费拉里法［45］进行求解。

首先，为了便于推导，命a（x0，y0，R）为K（x0，y0，R）的分子部分，命b（x0，y0，R）为K（x0，y0，R）的分母部分，式（12）可以写作

因为，b2＞0，因此

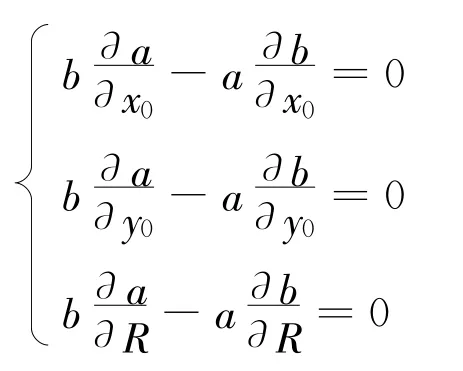
移项，得

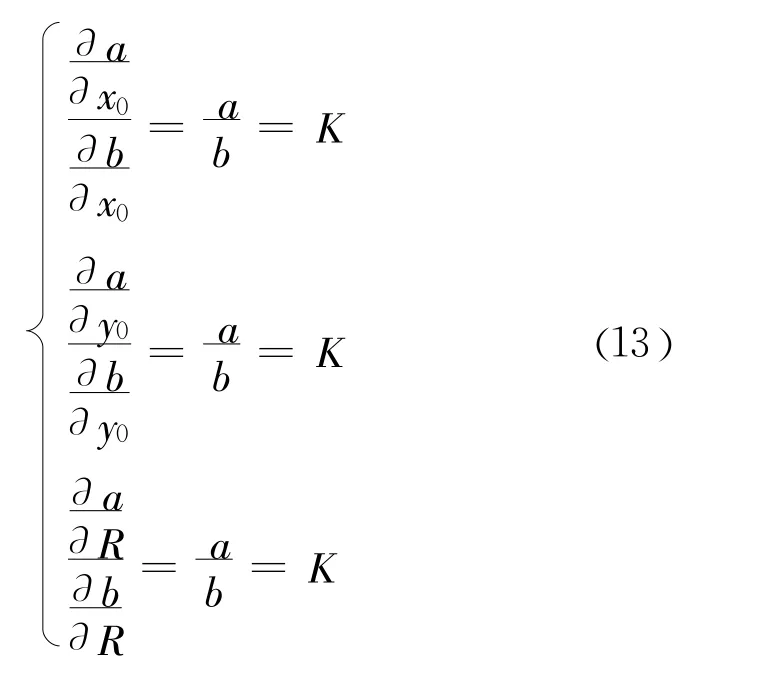
（xs，ys，Rs）便是式（13）的解。求解

可以看出，由于式（14）中存在反三角函数和根式，使得方程为超越方程，故而，需要对式（14）进行泰勒展开，使其转化为可解的多项式。

因为

故而，根据泰勒公式复合运算法则，可以进行二阶麦克劳林展开，

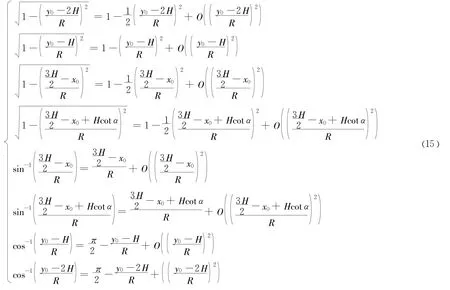
将式（15）中的高阶项截去，连同式（11），代入到式（10）中，得到

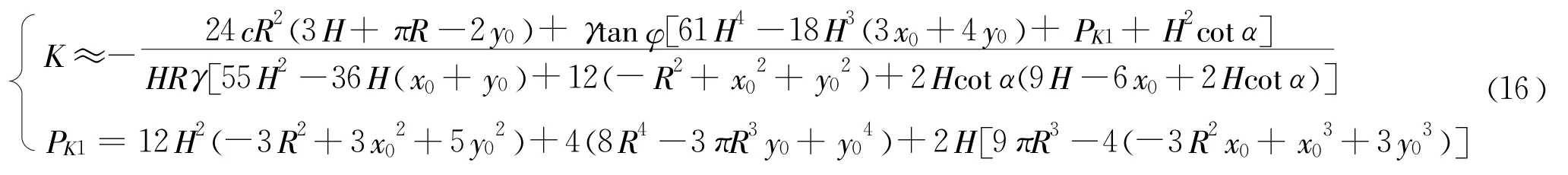
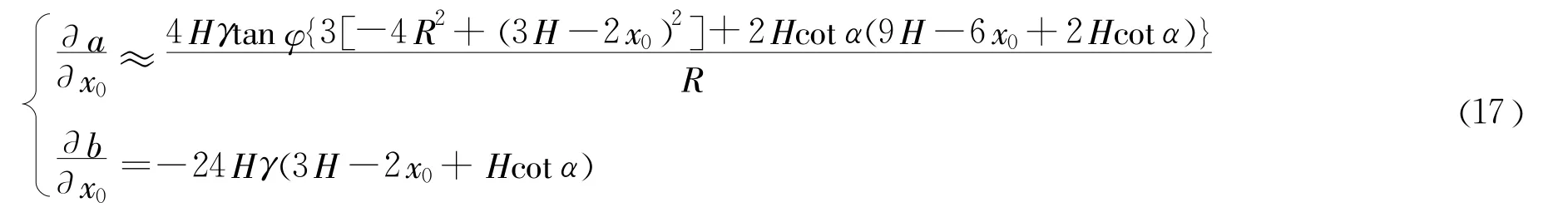
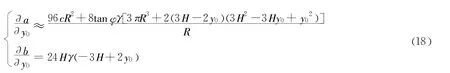
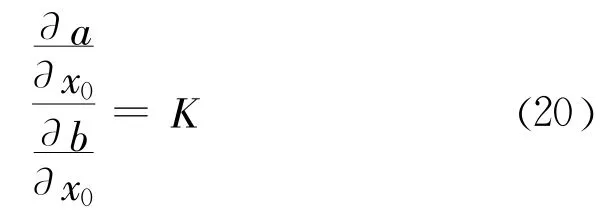
将式（16）和式（17）代入式（20），整理后得到如下形式

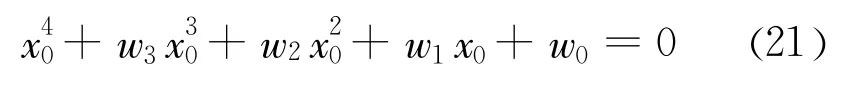
式（21）中，w3、w2、w1、w0皆为与x0无关的多项式。

根据置换群和盛金公式综合解法，需要解答

根据式（24），可以得到h，此时，

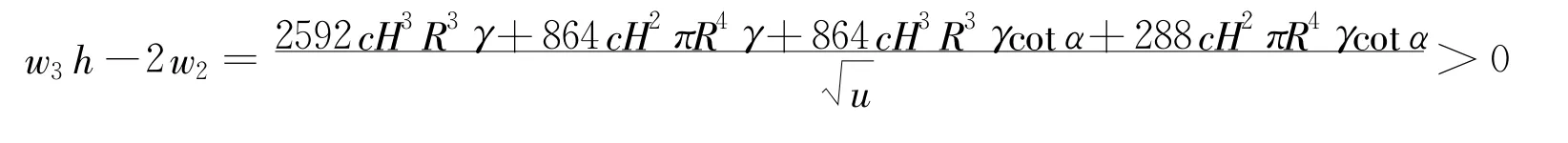
u是与x0无关的极其复杂的表达式，限于篇幅问题，没有给出表达式的具体细节。由此，根据盛金公式，只需要解答式（25）便能得到x0。

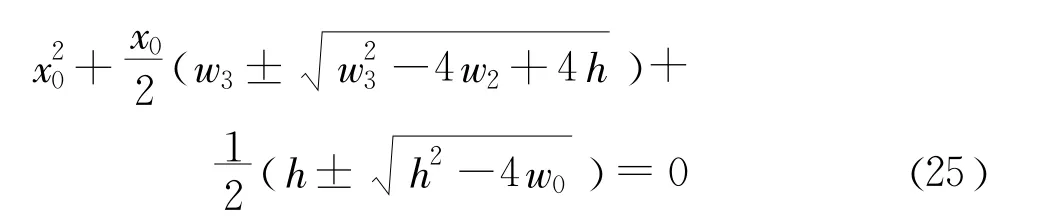
式（25）有四个解，但只有一个解是实数，该解为

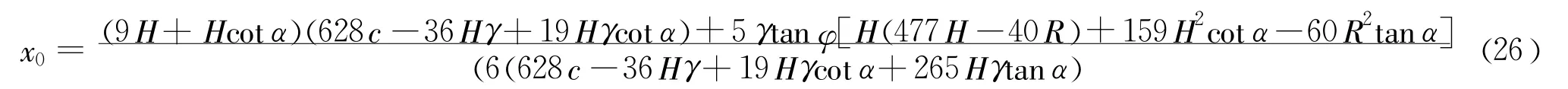
参照求解x0的步骤，以此类推，可以得到y0和R

联立式（26）、式（27）和式（28）并求解（在求解过程中，涉及到的最高次幂不超过4次，因此只需参展求解x0的过程便可），可以得到一个滑弧的位置参数（x0、y0、R），因为这是最危险滑弧，我们用（xs、ys、Rs）来表示此滑弧，以示区别。

其中

将式（29）代入式（10），便可得到Ks=K（xs，ys，Rs）。

3 算 例

3.1 与传统方法对比

根据卢廷浩《土力学》［46］的算例：一均质黏性土坡，高20 m，坡比1∶2，填土黏聚力c为45 kPa，内摩擦角为7°，重度为20 kN/m2。

《土力学》计算结果为Ks=1.19。

本文结果为Ks=1.13。

根据赵树德《土力学》的算例：高20 m的均质土坡，坡比1∶2，填土黏聚力c为10 kPa，内摩擦角为20°，重度为18 kN/m2。

《土力学》计算结果为Ks=1.34。

本文结果为Ks=1.09。

3.2 与数值方法作比较

参考张天宝［37］的《土坡稳定分析圆弧法的数值研究》的算例：一均质土坡，坡高H=50 m，重度γ= 20 kN/m2，坡比1∶3.25，内摩擦角tanφ=0.2，黏聚力c=60 kPa。

通过图5可以看出，对于传统的分条试算方法，由于其计算比较粗略，得到的结果往往与真实结果误差较大，笔者方法所计算的最小安全系数比文献［47］所得的最小安全系数低5%，更加安全。张天宝的结果是在构建积分模型的基础上，通过最优化方法寻找最小安全系数，这个结果已经非常贴近真实的Ks，笔者结果比其低0.3%，说明笔者方法在精确度和安全性上皆能完全满足工作需求。综上所述，笔者的方法所得的Ks比传统方法、数值方法所得到的Ks都安全，且足够精确。

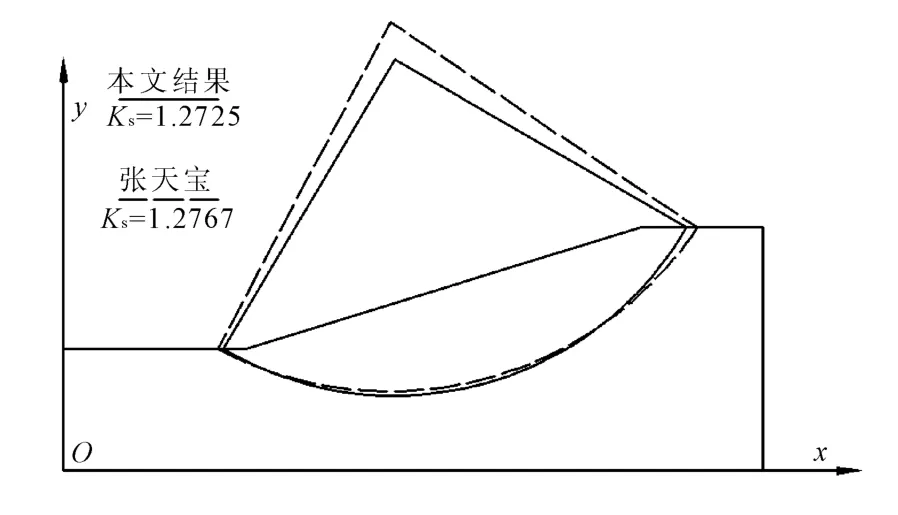
图5 本文结果和张天宝结果对比

4 结 论

针对Fellenius法，通过对其原有的连加数学模型进行分析，利用微分法建立了积分形式的数学模型K=K（x0，y0，R）。所得到的积分形式的数学模型在数理上比传统的连加数学模型更加精确。利用积分形式的数学模型，可以更加简便地计算最小安全系数Ks。

针对积分形式的数学模型，将求解最小安全系数Ks的问题转化为K（x0，y0，R）求极值问题，并导出了K（x0，y0，R）求极值时应满足的方程，只需要对方程进行求解便能得到最小安全系数Ks。此种做法完全脱离了传统计算方法中对于最危险滑弧的搜索，在数理层面上比以往的方法要精确，且大大减少了计算量。

针对gradK=（0，0，0）无根式解问题，通过麦克劳林公式将函数K进行简化，并利用费拉里公式对四次方程进行求解，得到了最危险滑弧的位置（xs，ys，Rs）的表达式。只需将相关参数代入（xs，ys，Rs）的表达式中，即可得到（xs，ys，Rs）的值，无需试算与解方程，极大提高了计算效率于精度。将所得到的（xs，ys，Rs）代入K函数中，便可得到最小安全系数Ks。而且，所得到的最小安全系数Ks比传统方法、于数值方法都要精确、安全。

［1］ Duncan J M.State of the art：Limit equilibrium andfinite element analysis of slopes［J］.Journal ofGeotechnical Engineering，1996，22（7）：577－596.

［2］ 方玉树.边坡稳定性分析条分法最小解研究［J］.岩土工程学报，2008，30（3）：331－335.

［3］ 中华人民共和国水利部.碾压式土石坝设计规范：SL274-2001［S］.北京：中国水利水电出版社，2001.

［4］ Basudhar P K.Some application of mathematical programming techniques to stability problems in Geotechnical Engineering［D］.Indian Institute of Technology，Kanpur，India，1976.

［5］ Baker R，Garber M.Variational approach to slope stability［J］.On Soil Mech and Found Engineering，1997，2：9－12.

［6］ Patra C R，Basudhar P K.Generalized solution procedure for automated slope stability analysis using inclined slices［J］. Geotechnical and Geological Engineering，2003，21（3）：259－281.

［7］ Fredlund D G，Krahn J.Comparison of slope stability methods of analysis［J］.Canadian Geotechnical Journal，1997，14（3）：429－439.

［8］ Graham J.Methods of stability analysis［J］.Brunsden and Prior，Slope Instability，JohnWiley&Sons Ltd.，1984：171－215.

［9］ Mostyn G R，Small J.Method of stability analysis，In：Walker and Fell（eds.），Slope Instability and Stabilisation，Balkema，Rotterdam，1987.

［10］ Nash D.A comparative review of limit equilibrium methods of stability analysis，In：M.G.Anderson and K.S. Richards（eds.），Slope stability，John Wiley and Sons Ltd，1987.

［11］ Wang Chenghua，XIA Xuyong.State-of-the-art：methods for searching critical slipsurface in slope stability analysis［J］.Building Science Research of Sichuan，2002，28（3）：34－39.

［12］ Revilla J，Castillo E.The calculus of variations applied to stability ofslopes［J］.Geotechnique，1977，27（1）：1－11.

［13］ Jong G D J D.Applicat ion of the calculus of variation to vertical cut off in cohesive frictionlesssoil［J］.Geotechnique，1980，30（1）：73－88.

［14］ Nguyen V U.Determinat ion of critical slope failure surface［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，1985，111（2）：238－250.

［15］ Denatale J S.Rapedidentification of critical slip surface：structure［J］.Journal of Geotechnical Engineering，ASCE，1991，177（10）：1568－1589.

［16］ Celestino T B，Duncan J M.Simplified search for non－circular slipsurface［C］//Soil Mech.and Found.Engrg.，Balkema A A，Rotterdam，The Netherlands，1981，3：391－394.

［17］ Arai K，Tagyo K.Determination of noncircular slip surface giving theminimum f actor of safety in slope stability analysis［J］.Soils andFounddat ions，1985，25（1）：43－51.

［18］ Li K S.White W.Rapid evaluation of the critical surface in slope stabilityproblems［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1987，11（5）：449－473.

［19］ Yamagami T，Ueta Y.Search for noncircular slip surfaces by the Morgenstern-Preice method［C］//Proc.of 6th Int. Conf.on Numerical Methodsin Geomechanics.Innsbruck，1988：1335－1340.

［20］ 陈祖煜，邵长明.最优化方法在确定边坡最小安全系数方面的应用［J］.岩土工程学报，1988（4）：1－13.

［21］ Greco V R.Numerical methods for locating the critical slip surface inslope stability［C］//Proc.of 6th Int.Conf.on Numerical Methods in Geomechanics.Innsbruck，1988：1219－1223.

［22］ Baker R.Determination of critical slip surface in slope stability computation［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1980，4（4）：333－359.

［23］ 曹文贵，颜荣贵.边坡非圆临界滑动面确定之动态规划法研究［J］.岩石力学与工程学报，1995，14（4）：320－328.

［24］ Yamagami T，Jiang J C.A search for the critical slip surface in three-dimensional slope stability analysis［J］.Soils and Foundations，1997，37（3）：1－16.

［25］ Boutrup E，Lovell C W.Search technical in slope stability analysis［J］.Engineering Geotechnical，1980，16（1）：51－61.

［26］ Siegel R A，Kovacs W D，Lovell C W.Random surface generation instability analysis［J］.International Journal of Rock Mechanics and Mining Science&Geomechanics Abstracts，1981，18（6）：126.

［27］ Greco V R.Efficient Monte Carlo technique for locating critical slipsurface［J］.Journal of Geotechnical Engineering，ASCE，1996，122（7）：517－525.

［28］ Malkawi A I H，Hassan W F，Sarma K S.Global search method for locatinggeneral slip surface using Monte Carlo Techniques［J］.Journal of Geotechnical and Geoenvironmental Engineering，ASCE，2001，127：688－698.

［29］ Chen Z Y.Random trials used in determining global minimum factors of safety of slopes［J］.International Journal of Rock Mechanics and Mining Science&Geomechanics Abstracts，1993，31（1）：225－233.

［30］ Anthony T G.Genetic algorithm search for critical slip surface in multiple－wedge stability analysis［J］.Canadiam Geotechnical Journal，1999，36（2）：382－391.

［31］ 弥宏亮，陈祖煜.遗传算法在确定边坡稳定最小安全系数中的应用［J］.岩土工程学报，2003，25（6）：671－675.

［32］ 李守巨，刘迎曦，何 翔，等.基于模拟退火算法的边坡最小安全系数全局搜索方法［J］.岩石力学与工程学报，2003，22（2）：236－240.

［33］ 李 亮，迟世春，林 皋.基于蚁群算法的复合形法及其在边坡稳定分析中的应用［J］.岩土工程学报，2004，26（5）：691－696.

［34］ 张 慧，李立增，王成华.粒子群算法在确定边坡最小安全系数中的应用［J］.石家庄铁道学院学报，2004，17（2）：1－4，10.

［35］ 陈云敏，魏新江，李育超.边坡非圆弧临界滑动面的粒子群优化算法［J］.岩石力学与工程学报，2006，25（7）：1443－1449.

［36］ 张天宝.土坡稳定分析圆弧法的数值研究［J］.成都工学院学报，1978（1/2）：97－122.

［37］ 黄文东.极限平衡条分法中边坡潜在滑动面搜索方法的改进［J］.世界采矿快报，1999（9）：42－44.

［38］ 杨庚宇，赵少飞.土坡稳定分析圆弧滑动法的解析解［J］.工程力学，1988（S1）：440－444.

［39］ Cao Jinggang，Zhang M M.Shotcommunications：analytical method for analysis of slope stability［J］.International Journal for Numerical&Analytical Methods in Geomethanics，1999，23（5）：439－449.

［40］ 李同录，李 萍，郑书彦.土坡稳定分析圆弧法的解析解及应用［J］.煤田地质与勘探，2004，32（5）：29－32.

［41］ 蒋斌松，蔡美峰，吕爱钟.边坡稳定性的解析计算［J］.岩石力学与工程学报，2004，23（16）：2726－2729.

［42］ 韩晓雷，任宇涛，李素娟.基于遗传算法的土坡稳定性分析数值解研究［J］.工业建筑，2009，39（S1）：714－716.

［43］ 张向东，张哲城，张 玉，等.瑞典圆弧法的积分形式及其广义数学模型［J］.应用力学学报，2014，31（1）：162－168.

［44］ http：//en.wikipedia.org/wiki/%C3%89variste-Galois

［45］ 叶其孝，沈永欢.实用数学手册［M］.2版.北京：科学出版社，2006.

［46］ 卢廷浩.土力学［M］.2版.南京：河海大学出版社，2005.

The Analytical Solution of Fellenius Method

LI Chuang1，ZHAO Shengjie1，DONG Ye2，LI Pengyu2，MU Mengjing2
（1.HYDROLANCANG，Lincang，Yunnan 675805，China；2.North China Electric Power University，Beijing 102206，China）

Fellenius method is a classical solution which hasbeen widely used in engineering construction.Numerical methods are more and more popular at the moment，which divide a lot of stripes and traverse the sliding surface to calculate the minimum safety factor and the location of the most dangerous sliding surface（center coordinates and radius）. However，the numerical methods need a large amount of computation time and the accuracy of the numerical methods is less than the analytical calculation methods.This work try to get the analytical formula of safety factor Kswhich is the function of the center coordinates（x0，y0）and the radius R.By soloving the equation gradKs=（0，0，0），we can get the center coordinates（x0，y0）and the radius R and we can also get the minimum safety factor Ksmin.A program“LCSLOPE”was developed to calculate gradKs=（0，0，0）analytic solution.This program“LC-SLOPE”does not distinguish between homogeneous slope and stratified slope and has no theoretical error.In order to get a result which is easy for the engineering staff to use and accurate，for homogeneous slope，it can be simplified as grad Ks=（0，0，0）by taylor formula and get the Ksmin，（x0，y0）and R.

slope stability；Fellenius method；the analytical solution；complex slope

TU43

A

1672—1144（2016）05—0202—09

10.3969/j.issn.1672-1144.2016.05.039

2016－07－02

2016－08－06

李 闯（1990—），山东荷泽人，硕士，主要从事水工结构、非均质材料冲击特性方面的研究。E－mail：976308589@qq.com