边坡局部稳定性变化规律的研究

刘路路，王东英，宋 亮，钟国强

（1.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，湖北武汉430071；2.中国科学院大学，北京100000；3.贵州省交通规划勘察设计研究院股份有限公司，贵州贵阳550081）

边坡局部稳定性变化规律的研究

刘路路1，2，王东英1，2，宋 亮3，钟国强1，2

（1.中国科学院武汉岩土力学研究所岩土力学与工程国家重点实验室，湖北武汉430071；2.中国科学院大学，北京100000；3.贵州省交通规划勘察设计研究院股份有限公司，贵州贵阳550081）

现有边坡稳定性分析方法大多假定边坡滑面各部位的安全系数相等，既不能反映边坡潜在滑面上稳定系数的分布规律，也不符合工程实际情况。分别基于超载储备安全系数定义和强度储备安全系数定义研究了边坡局部稳定性变化规律，并分析了滑体条块数目以及滑面形状对边坡局部稳定性分布规律的影响。此外，还提出了由局部稳定系数求解整体稳定系数的加权方法。研究结果表明：滑体条块的划分数量对边坡局部稳定性的分布规律几乎没有影响，而滑面形状对其影响较大；取微段下滑力占各微段下滑力代数和的比值作为权重，是由边坡局部安全系数加权计算整体安全系数的最优加权方法。

局部稳定系数；滑体条块数目；滑面形状；加权方法

常用的边坡稳定性分析方法依据不同的安全系数定义，可以归结为两大类：基于超载储备安全系数定义的边坡稳定性分析方法［1-2］；基于强度储备安全系数定义的边坡稳定性分析方法［3-5］。这两类分析方法在计算安全系数时，均假定滑面不同部位的局部安全系数相等［6］。但这种假定并不符合实际，Wright S G等［7］、Tavenas F等［8］、Chugh A K等［9］对依据强度储备定义的极限平衡法进行了研究，发现滑动面不同部位的局部安全系数并不相等。滑面不同部位的破裂角不同，沿破裂角方向的安全系数值最小，其余方向的安全系数均比该方向的安全系数大，因此，滑面不同方向的局部安全系数也不相等。在基于超载储备定义的分析方法中，通过增大荷载使边坡达到极限状态。但增大荷载滑动面上的下滑力和抗滑力并非同比例增大，由此所得到的超载安全系数也不相等，刘艳章［10］指出这种分析方法的安全系数具有明显的方向性。

此外，现有的边坡稳定性分析方法均建立在“平均”安全系数的基础上，不能反映边坡潜在滑面上安全系数的分布规律。对此，杨涛等［11-12］研究了滑坡稳定性分析点安全系数法及其应用条件，分析了滑坡的空间滑动机制。张占容等［13］分析了不同应力路径下对应的点安全系数，推导了其表达式以及在应力空间的表现形式。郑文棠［14］分别使用FLAC3D强度折减法和点安全系数法进行了边坡稳定性分析，并对两种方法计算结果的精确性和可靠性进行了评价。综上所述，对于边坡局部稳定性的研究已经取得了一定成果，但对于计算边坡局部安全系数的影响因素及局部安全系数在滑面上分布规律的研究较少。基于该问题本文对潜在滑面上各部分的稳定性进行了探索，得出了边坡局部稳定系数的分布规律，用不同计算方法分析了滑体条块划分数量及滑面形状对均质边坡局部稳定性的影响。提出了通过局部稳定系数求解边坡整体稳定系数的加权平均方法，并将计算结果与传统的极限平衡法［15-18］进行了对比分析，发现计算结果较为相近，表明该种方法是可行的，这对于边坡稳定性分析具有很大的参考价值。

1 边坡局部安全系数的定义

常用的安全系数定义有两种：超载储备安全系数、强度储备安全系数。超载安全系数的定义为：为了使边坡达到极限状态，将边坡荷载增大FP倍，使下滑力和抗滑力同时增大，当下滑力和抗滑力相等时即认为边坡达到了极限平衡状态，取这时的荷载增大倍数FP为超载安全系数［19］；强度储备安全系数的定义为：为了使边坡达到极限状态，将边坡材料的强度参数减小Fs倍，减小抗滑力的大小至和下滑力相等时即认为边坡达到了极限平衡状态，取强度参数减小倍数Fs为强度折减安全系数［19］。

取潜在滑体上某一条块作为研究对象，条块受力情况如图1所示。图中Ui、Ui+1分别为上下相邻条块对该条块的法向作用力，Xi、Xi+1分别为上下相邻条块对该条块的切向作用力，Gi为条块自身重力，Ni为滑面对条块的法向作用力，Ti为滑块下滑力，Ri为滑面对滑体提供的抗滑力。由强度储备安全系数定义，在滑面微段上平衡条件应为Ti=Ri/F=（cili+Nitanφ）/F；由超载储备定义，滑面微段上平衡条件应为FTi=Ri=cili+Nitanφ。两种定义的安全系数公式均为：

图1 滑体上条块力学模型

边坡局部稳定系数Fi为：潜在滑面上各微段的抗滑力与下滑力之比。由式（1）可得局部安全系数的表达式为：

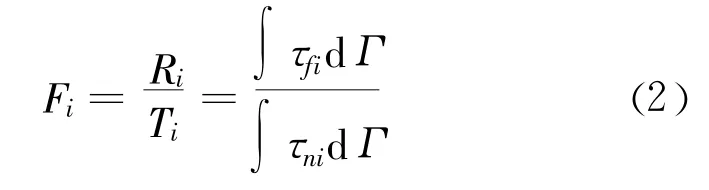
式中：τfi为滑面微段上的抗剪强度；τni为滑面微段上剪切力；dΓ为滑面微段长度。

假设微段上抗剪强度、剪切强度为一常数且将微段近似为直线，则有：

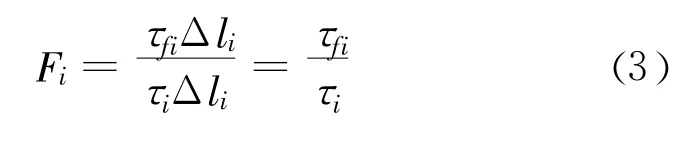
2 边坡局部稳定性变化规律研究

2.1 滑块数目对边坡局部稳定系数分布的影响分析

为分析边坡潜在滑体上条块划分数目对边坡局部稳定系数分布规律的影响，对文献［20］中均质土坡算例的滑体分别划分为10、30、50等份，采用局部安全系数公式（3）计算边坡局部稳定系数，并分析边坡潜在滑面上局部稳定系数的变化规律。

（1）计算模型及相应的材料参数

计算模型形状和尺寸见图2，边坡材料参数的黏聚力为c=58.86 kPa，摩擦角φ=11.31°，重度γ=19.62 kN/m3，弹性模量和泊松比分别为E=80 MPa、μ=0.43。采用非关联流动法则，边界条件为底部约束，两侧面为法向约束，只考虑重力作用，潜在滑面采用极限平衡法搜索得到。

（2）计算结果分析

不同条块数对边坡局部稳定性分析结果见图3。从图3中可以看出，划分不同数量的条块，滑体的局部稳定性计算结果很接近，这说明滑体条块的划分数量不影响边坡局部稳定性的分布规律。从图3中可以看出，滑体条块划分的越细，坡顶位置处的稳定系数越高。除坡顶处局部稳定系数较高之外，其他位置的边坡局部稳定情况相近，没有极端峰值。据此可得出圆弧滑面的边坡局部稳定性变化规律：越靠近剪出口，边坡局部稳定性越低；越靠近坡顶，局部稳定性越高；中间呈上凸趋势属于过渡区。

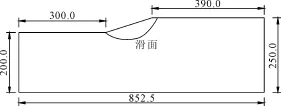
图2 均质土坡计算模型

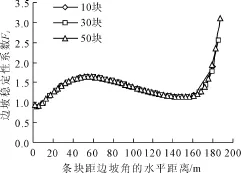
图3 不同条块数对边坡局部稳定性分析结果的影响

2.2 潜在滑面形状对边坡局部稳定系数分布的影响分析

为了分析潜在滑面形状对边坡局部稳定系数分布规律的影响，分别采用超载储备定义和强度储备定义的局部安全系数公式计算均质土坡圆弧滑面、直线滑面及折线滑面的安全系数。

计算模型及材料参数同样采用文献［20］中均质土坡算例。滑面形式如图4所示。

图4 均质土坡滑面形状

计算结果见图5。从图5中可以看出，折线滑面和圆弧滑面所得边坡局部稳定性变化规律较为相似。而直线滑面的计算结果差异较大，特别是在靠近坡顶处出现先增大后减小的趋势，且局部稳定系数较高，这可能是直线滑面该部位距离实际危险滑面部位较远所致。从图5各曲线走势可以看出，对于均质土坡局部稳定系数的计算，圆弧滑面的计算结果最理想，折线滑面次之，直线滑面较差，这说明滑面形状对边坡滑体上部局部稳定性计算结果影响较大。从曲线走势也可看出：边坡局部稳定性靠近坡顶处稳定性较高，靠近坡脚稳定性较差。

图5 不同滑面形状对边坡局部稳定性分析结果的影响

3 由边坡局部稳定系数求解整体稳定系数

对边坡局部安全系数Fi进行加权处理求得整体安全系数Fs，加权处理公式如下：

式中：ωi为各微段局部稳定系数的权重。

3.1 加权方法

本文采用了四种加权方法计算边坡的整体稳定系数，各种方法介绍如下：

（2）取微段长度li占滑面总长度的比值为权重，即取，则整体安全系数的表达式为：

（3）取微段下滑力Ri占各微段下滑力代数和的比值为权重，即取，则整体安全系数的表达式为：

（4）取微段抗滑力Ti占各微段抗滑力代数和的比值为权重，即取则整体安全系数的表达式为：

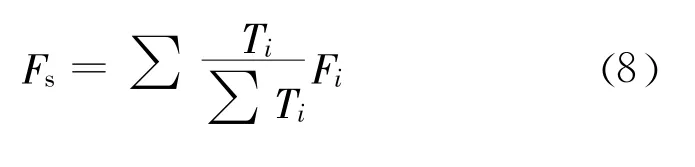
3.2 加权方法对比分析

分别采用四种加权方法对第2节中局部稳定系数进行加权计算，并将计算结果与极限平衡法计算的稳定系数进行对比，现将计算结果汇总如表1所示。

表1 边坡整体稳定系数计算结果

从表1计算结果可知，采用第三种加权方法加权得到的结果较为理想，与极限平衡法的计算结果符合较好，其他三种加权方法的计算结果波动较大与极限平衡结果差异较大。这说明取微段下滑力占各微段下滑力代数和的比值为权重，对边坡局部稳定系数进行加权计算得到边坡整体稳定系数较为合理。

4 结 论

（1）滑体条块划分数目对边坡局部稳定性变化规律没有影响；对于均值土坡圆弧滑面，越靠近剪出口，边坡局部稳定性越低；越靠近坡顶，局部稳定性越高；中间呈上凸趋势属于过渡区。

（2）对于均质土坡局部稳定系数的计算，滑面形状对边坡滑体上部局部稳定性影响较大，对滑体中部和下部影响较小。圆弧滑面的计算结果最理想，折线滑面次之，直线滑面较差，这说明滑面形状对边坡滑体上部局部稳定性计算结果影响较大。

（3）本文提出了四种对局部稳定系数的加权方式，根据算例计算结果分析可知：取微段下滑力占各微段下滑力代数和的比值作为权重，是由边坡局部安全系数加权计算整体安全系数的最优加权方法。

［1］ Chen W F，Liu X L.Limit Analysis in Soil Mechanics［M］. Amsterdam：Elsevier Science，1990.

［2］ 中华人民共和国建设部.建筑边坡工程技术规范：GB 50330-2002［S］.北京：中国建筑工业出版社，2002.

［3］ 郑颖人，赵尚毅.有限元强度折减法在土坡与岩坡中的应用［J］.岩石力学与工程学报，2004，23（19）：3381－3388.

［4］ 郑 宏，李春光，李焯芬，等.求解安全系数的有限元法［J］.岩土工程学报，2002，24（5）：626－628.

［5］ 罗青海.比较两种折减法在岩质边坡稳定性分析中的

差异［J］.水利与建筑工程学报，2015，13（3）：213－216.

［6］ 郑 宏，田 斌，刘德富，等.关于有限元边坡稳定性分析中安全系数的定义问题［J］.岩石力学与工程学报，2005，24（13）：2225－2230.

［7］ Wright S G，Kulhawy F G，Duncan J M.Accuracy of equilibrium slope stability analysis［J］.Journal of the Soil Mechanics and Foundations Division，ASCE，1973，99（10）：783－791.

［8］ Tavenas F，Trak B，Leroueil S.Remarks on the validity of stability analyses［J］.Canadian Geotechnical Journal，1980，17（1）：61－73.

［9］ Chugh A K.Variable factor of safety in slope stability analysis［J］.Geotechnique，1986，36（1）：57－64.

［10］ 刘艳章.边坡与坝基抗滑稳定的矢量和分析法研究［D］.湖北武汉：中国科学院武汉岩土力学研究所，2007.

［11］ 杨 涛，周德培，马惠民，等.滑坡稳定性分析的点安全系数法［J］.岩土力学，2010，31（3）：971－975.

［12］ 杨 涛，马惠民，代 杰，等.滑坡稳定性分析点安全系数法的应用条件［J］.西南交通大学学报，2011，46（6）：966－972.

［13］ 张占荣，朱泽奇，杨艳霜，等.基于不同应力路径的点安全系数研究［J］.隧道建设，2009，29（6）：626－628.

［14］ 郑文棠.基于FLAC3D的强度折减法和点安全系数法对比［J］.水利与建筑工程学报，2010，8（4）：54－57.

［15］ 刘志楠.极限平衡法的边坡稳定分析研究［D］.合肥：合肥工业大学，2006.

［16］ 张津生.浅析刚体极限平衡法［J］.水力发电学报，2005，24（5）：26－33.

［17］ 陈革强.刚体极限平衡法浅析［J］.海河水利，1999（2）：16－20.

［18］ 孙 超，吕一彦，吴继敏.大型堆积体边坡极限平衡稳定性分析［J］.水利与建筑工程学报，2014，12（1）：147－150.

［19］ 潘家铮.建筑物的抗滑稳定和滑坡分析［M］.北京：水利出版社，1980.

［20］ 孙冠华，郑 宏，李春光.基于等效塑性应变的边坡滑面搜索［J］.岩土力学，2008，29（5）：1159－1163.

Variable Rule of Slope Local Safety Factor

LIU Lulu1，2，WANG Dongying1，2，SONG Liang3，ZHONG Guoqiang1，2
（1.State Key Laboratory of Geomechanics and Geotechnical Engineering，Institute of Rock and Soil Mechanics，Chinese Academy of Sciences，Wuhan，Hubei 430071，China；2.University of Chinese Academy of Sciences，Beijing 100000，China；3.Guizhou Provincial Communications Planning&Survey and Design Institute Co.，Ltd.，Guiyang，Guizhou 550081，China）

Most of the methods of slope stability analysis assume that each part of the sliding surface of slope has the same safety factor，which not only fails to reflect the distribution rule of stability coefficient of the slope slip surface but also fails to accord with the reality of the slope program.We have studied the distribution rule of slope local stability based on the safety factor definition of the over－loading reserve and strength reserve，respectively，and we also analyzed the influence of the sliding block number and shape of sliding surface to the distribution rule of slope local stability.Besides we proposed the weighted method to solve the global safety factor by local ones.The study shows that the amount of the sliding block has negligible influence on the distribution rule of slope local stability，but the shape of the sliding surface has great one.Furthermore，it is reasonable to make the ratio of micro section slide force and the sum of all of the micro section slide force as the weight to solve the global safety factor by local ones.This paper studies the influence of the sliding body slice number and sliding surface form on the distribution of local slope stability，summarized the method of weighted integral stability coefficient by local stability coefficients.

local stability coefficient；sliding body slice number；sliding surface shape；weighted method

TU443

A

1672—1144（2016）05—0041—04

10.3969/j.issn.1672-1144.2016.05.008

2016－06－06

2016－07－01

国家自然科学基金资助项目（51509243）

刘路路（1991—），男，山东济宁人，硕士研究生，研究方向为涉水滑带劣化机理。E－mail：401193222@qq.com。