投影寻踪模型在行蓄洪区运用风险评价中的应用

黄健元,金广宇,于彦博

(1.河海大学公共管理学院,江苏 南京 210098; 2.淮河水利委员会水利水电工程技术研究中心,安徽 蚌埠 233001)



投影寻踪模型在行蓄洪区运用风险评价中的应用

黄健元1,金广宇1,于彦博2

(1.河海大学公共管理学院,江苏 南京 210098; 2.淮河水利委员会水利水电工程技术研究中心,安徽 蚌埠 233001)

将行蓄洪区运用风险评价指标体系应用于基于信息熵的投影寻踪模型,得到风险评价投影值。根据结果把淮河干流行蓄洪区运用风险等级分为4类,风险等级及分类区间从高到低依次为Ⅰ级,投影值≥4.16,包括4个蓄洪区和寿西湖、鲍集圩2个行洪区;Ⅱ级,投影值为4.10～4.16,包括汤渔湖等4个行洪区;Ⅲ级,投影值为3.90～4.16,包括香浮段等7个行洪区;Ⅳ级,投影值为0～3.90,包括邱家湖等4个行洪区。

信息熵;投影寻踪模型;风险等级;行蓄洪区

行蓄洪区运用风险评价是实际运用决策中的基础工作。一直以来,对行蓄洪区运用风险的研究方法各不相同,李绍飞等[1]建立了以致灾因子、孕灾环境、承载体属性三方面为基础的蓄滞洪区洪灾风险评价指标体系,并制定了洪灾风险等级评价标准。包君等[2-3]根据行蓄洪区的运用风险特征,从社会风险、经济风险、行洪危险和承灾能力等4个方面,构建了包括16项指标的行蓄洪区运用风险综合评价指标体系,分别利用模糊ISODATA聚类分析法和基于模糊优选模型、决策优选方法的混合模型对淮河流域21个行蓄洪区的运用风险进行评价,将淮河干流行蓄洪区从高到低分为5个风险等级。

与以往研究不同,考虑到风险评价指标在一定程度上存在着相关性,本文利用基于信息熵的投影寻踪模型对行蓄洪区运用风险进行评价,得到有关行蓄洪区运用风险的相对水平值,并划分淮河干流21个行蓄洪区的运用风险等级。混合模型是对典型行蓄洪区运用风险进行综合评价,对比分析各相关行蓄洪区运用时的风险因素;模糊ISODATA聚类分析法是对调研获取的数据对应的风险进行聚类分析,将行蓄洪区运用风险分类管理;而基于信息熵的行蓄洪区运用风险评价投影寻踪模型是得到有关行蓄洪区运用风险的相对水平值。上述3种评价方法在发挥各自价值的同时,可以相互校验,使得评价结果更为合理。

1 行蓄洪区运用风险评价指标体系与评价指标值采集

包君等[2-3]分别利用模糊ISODATA聚类分析法和基于模糊优选模型、决策优选方法的混合模型对淮河干流行蓄洪区运用风险进行聚类、排序分析,而本文利用投影寻踪模型对淮河干流行蓄洪区运用风险进行相对水平值计算。为了更好地比较,故直接采用已有行蓄洪区运用风险综合评价指标体系(见表1)[2]，评价指标值也直接采用已有相关指标数据[2]。

2 投影寻踪模型

传统的统计评价方法只适用于2个或者3个评价对象等较少指标的综合评价,而投影寻踪法因其具有适用范围广、灵活简单等优点,在风险评价中始终占据着重要位置,适用于多指标、多个评价对象、复杂化的风险评价。行蓄洪区风险评价指标体系中含有多个指标,并且作为评价对象的行蓄洪区也有多个,因此,运用投影寻踪方法评价行蓄洪区的运用风险显然是合适的。

投影寻踪聚类技术[4]实质上是一种将高维数据投影到低维子空间上的降维处理技术,即将影响问题的多因素指标通过投影寻踪聚类分析,得到反映其综合指标特性的投影特征值,进而建立投影特征值与因变量的一一对应关系函数。通过优化投影指标函数,求出能反映原高维数据结构和特征的投影向量,分析低维数据来达到研究和分析高维数据的目的。

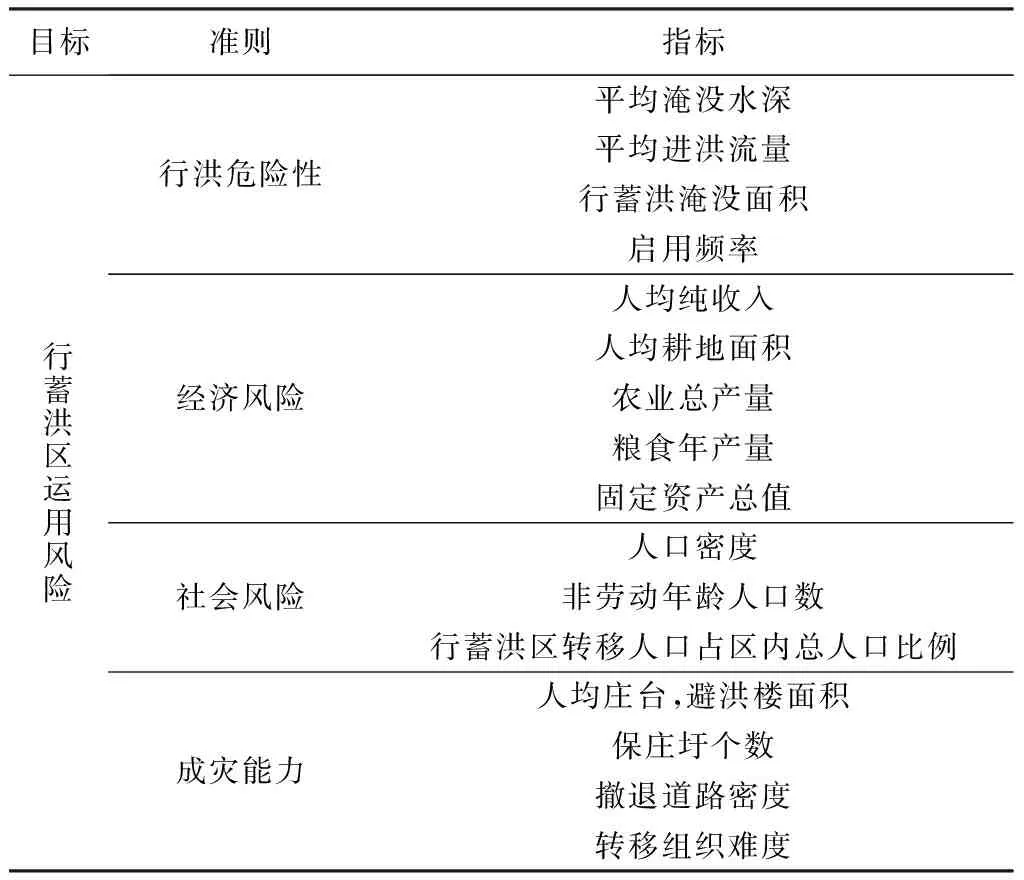
表1 行蓄洪区运用风险评价指标体系

2.1 指标值的无量纲化处理

假设第i个样本的第j个指标为x*(i,j)(i=1,2,…,n;j=1,2,…,p),其中n,p分别为样本的个数和指标的数目。为消除各指标的量纲和统一各指标值的变化范围,可利用极值归一化处理法。

对于越大越优的指标:

(1)

对于越小越优的指标:

(2)

式中:xmax(j)和xmin(j)分别为第j个指标值的最大值和最小值;x(i,j)为指标特征值归一化的序列。

转移组织难度指标运用模糊一致矩阵[5]进行量化处理并利用映射

将优度值si(i=1,2,…,21)转化为在[0,1]中取值的优属度ri。优属度越高行蓄洪区运用风险越高。计算结果见表2。

表2 转移组织难度优属度

2.2 线性投影

(3)

根据z(i)的一维散布图可进行分类,其中a为单位长度向量。投影向量的大小实际上反映了各评价指标对评价等级的影响程度。根据Jaynes[6]最大熵原理,在只能掌握部分信息的情况下要对概率分布做出推断,应取满足约束条件同时使信息熵值最大的概率分布,熵值越大意味着人为添加的约束和假设越少。因此,可构造最大熵目标函数如下:

(4)

(5)

式中:Sa为z(i)的标准差;Da为z(i)的局部密度。即:

(6)

(7)

2.3 投影函数最优化

当各指标值的样本集给定时,Q(a)只随投影方向a的变化而变化。不同的投影方向反映不同的数据结构特征,而最佳的投影方向就是最大可能暴露高维数据某类特征结构的投影方向。因此可以通过求解投影指标函数最大化问题来估计最佳投影方向。

最大化目标函数:

maxQ(a)=H(a)SaDa

(8)

约束条件:

(9)

这是一个复杂的非线性最优化问题,此处运用粒子群优化算法来求解这一寻优问题。

2.3.1 粒子群优化算法原理

粒子群算法(PSO)处理优化问题时,类似于在D维空间中搜索以一定质量飞行的粒子。空间中的各个粒子都有各自的位置和飞行速度,各个粒子都了解自己到目前为止搜索到的最好位置和整个群体内部其他粒子的历时最好点,看作粒子同伴的经验。各个粒子都随着最优粒子进行搜索。如果获得较好的解,则以较好的解为起始依据寻找下一个解[8]。

2.3.2 粒子群优化算法建立过程

随机为m个粒子产生初始速度和初始位置后,假设D维搜索空间中第i个粒子的位置为:Xi=(xi1,xi2,…,xiD),速度为:Vi=(vi1,vi2,…,viD)(1≤i≤m)。迭代过程中,第i个粒子经历的最好点记为Pi=(pi1,pi2,…,piD);整个粒子群所经过的最好点记为Pg=(pg1,pg2,…,pgD)。根据跟踪的两个最优解粒子不断更新自己,速度和位置变化公式如下:

(10)

(11)

式中:w为惯性系数,防止算法过早收敛;c1、c2为学习因子，通常c1=c2=2;ξ和η是定义在[0,1]区间上的伪随机数。

该算法的一般步骤为:①粒子群初始化;②估算粒子群中粒子的适应值;③对比粒子与它所经历最佳位置的适应值,若更好则替代原位置;④比较所有粒子所经历最好位置的适应值,将最好的值对应的位置作为当前的全局最好位置;⑤用式(10)、式(11)更新粒子的位置和速度;⑥若未达到终止条件,则回到第②步继续进行迭代计算。通常达到足够好的适应值或者预先设计的最大迭代次数则终止计算。

2.4 等级评价

获得最佳投影方向后,可求各个样本点的投影值z*(i),根据z*(i)的值进行从大到小排序或对各个样本点进行分类。

3 基于投影寻踪模型的行蓄洪区运用风险评价结果分析

借助MATLAB仿真,利用投影寻踪模型对行蓄洪区运用风险进行评价。选取不同的迭代次数和迭代步长求解投影函数的最大值。其中,粒子群中粒子数为21,最大迭代次数为100。部分计算结果见表3。

表3 不同迭代次数和步长下的投影函数最大值

从表3的计算结果中发现投影函数的最大值为155 122.0773。因此最佳投影方向为(0.157 2,-0.770 6,0.349 6,0.838 3,-0.350 7,0.801 1,0.138 4,0.200 9,0.608 3,-0.172 0,-0.349 5,0.104 5,0.833 6,0.600 3,0.809 1,0.510 0),将最佳投影方向代入模型中,计算样本数据的投影值,计算结果见表4。

表4 淮河干流行蓄洪区运用风险评价投影值

为了方便把投影寻踪模型与模糊ISODATA方法和混合模型进行比较,根据表4中的投影值大小可将行蓄洪区的运用风险分为4类,风险等级及分类区间从高到低依次为Ⅰ级(投影值≥4.16),Ⅱ级(投影值为4.10～4.16),Ⅲ级(投影值为3.90～4.16),Ⅳ级(投影值为0～3.90)。不同的风险等级代表启用该类行蓄洪区时会带来不同程度的经济风险和社会风险,造成不同程度的洪灾损失(包括直接损失和间接损失)。如Ⅰ级行蓄洪区指启用该类行蓄洪区行蓄洪时带来的经济风险和社会风险最大,造成的损失最高。对应的Ⅳ级行蓄洪区启用时洪水淹没造成的损失最小。

结合淮河干流行蓄洪区实际情况对21个行蓄洪区运用风险进行分级,其等级具体划分结果见表5。

根据结果可知:4个蓄洪区中,城西湖是淮河中游蓄洪量最大的蓄洪区,蓄洪量达29.5 亿m3,被誉为淮河防汛的最后一张王牌。瓦埠湖蓄洪区是淮河中游面积最大的蓄洪区,耕地面积广阔。2020年瓦埠湖规划人口40.77万人,蓄洪时转移人口多。蒙洼和城东湖粮食年产量分别为8.52万t和10.97万t,因此4个蓄洪区在运用时都具有Ⅰ级风险。可见蓄洪区都有高的运用风险。

表5 淮河干流行蓄洪区运用风险等级划分结果

行洪区中的鲍集圩、寿西湖两个行洪区因经济水平相对较高、固定资产总值高、行蓄洪时人口转移比例大、人均避洪设施面积小等因素导致其运用风险为Ⅰ级风险。邱家湖和下六坊因经济水平相对落后、人均安全设施面积大、撤退时转移人口比例小等因素综合作用而使运用风险等级为Ⅳ级风险。上六坊和洛河洼在运用时无须转移人口,行洪阻力较小,因此,运用风险等级为Ⅳ级风险。汤渔湖、潘村洼和临北段3个行洪区因经济水平相对较高、固定资产总值较高、行蓄洪时人口转移比例较大、人均避洪设施面积小等因素导致其运用风险为Ⅱ级风险。方邱湖农业总产值和固定资产总值较高,因此其运用风险为Ⅱ级风险。其他行洪区运用风险略低于方邱湖,处于Ⅲ级风险水平。因此,在启用行蓄洪区时,应优先考虑风险等级较低的行洪区,再考虑启用蓄洪区。

4 结 论

a. 通过比较3种模型结果分析发现:淮河干流4个蓄洪区的运用风险都较高,处于高或较高水平。行洪区中寿西湖、鲍集圩等处于高风险水平,洛河洼、上六坊堤、下六坊堤等运用风险处于较低或低水平。不论从3种模型的对比来看,还是参照历年运用情况和调整规划方案,都说明评价结果具有一定的合理性。基于指标体系和相关指标值,利用基于信息熵的行蓄洪区运用风险评价投影寻踪模型,得到有关行蓄洪区运用风险的相对水平值,对行蓄洪区的运用风险从高到低进行等级划分是行蓄洪区运用风险评价方法选择的又一尝试,并且可以通过投影寻踪模型、混合模型和模糊ISODATA聚类分析法三者相互校验,使得评价结果更为合理。行蓄洪区运用风险评价投影寻踪模型的建立,旨在引进一种新的行蓄洪区运用风险评价方法,是对已有评价方法的有益补充。

b. 运用投影寻踪模型对淮河干流行蓄洪区的运用风险进行评价分析,结果如下:4个蓄洪区在运用时全具有Ⅰ级风险,风险等级高,寿西湖、鲍集圩两个行洪区也属于Ⅰ级风险;汤渔湖、潘村洼、临北段、方邱湖4个行洪区属于Ⅱ级风险,风险等级较高;邱家湖、下六坊、上六坊、洛河洼4个行洪区属于Ⅳ级风险,风险等级低;其余7个行洪区属于Ⅲ级风险,风险等级较低。

c. 本研究仍存在不足之处:首先,各指标之间存在一定程度的相关性。其次,利用投影寻踪模型的计算量较大,并且将高维数据投影到低维子空间上,必然造成一些原始信息的损失。因此,在对高维数据进行降维的过程中,如何保持原数据信息的完整性,是需要进一步研究解决的问题。

[1] 李绍飞,于萍,孙书洪. 基于神经网络的蓄滞洪区洪灾风险模糊综合评价[J]. 中国农村水利水电,2008(6):60-64.

[2] 包君,黄健元. 基于改进ISODATA的行蓄洪区运用风险评价[J]. 人民黄河,2014,36(7):41-44.

[3] 包君,王再明. 混合模型在行蓄洪区运用风险评价中的应用[J]. 中国农村水利水电,2015(3):95-97.

[4] 王兆礼,赖成光,陈晓宏. 基于熵权的洪灾风险空间模糊综合评价模型[J]. 水力发电学报,2012,31(5):35-40.

[5] 刘群昌,许迪,谢崇宝,等. 波涌灌溉技术田间适应性分析[J]. 农业工程学报,2002,18(1):35-40.

[6] JAYNES E T. Information theory and statistical mechanics[J]. Physical Review,1957,106:620-630.

[7] 霍映宝,韩之俊. 基于广义最大熵原理和遗传算法的多指标权重确定方法研究[J]. 数理统计与管理，2005,24(3):40-42.

[8] 张双虎,黄强,吴洪涛,等. 水电站水库优化调度的改进粒子群算法[J]. 水力发电学报，2007,26(1):2-4.

水利部公益性行业科研专项经费项目(201301065)

黄健元(1964—),男,江苏溧阳人,教授,主要从事公共管理、统计学等研究。E-mail:hjy1964@sina.com

10.3880/j.issn.1003-9511.2016.05.014

P426

A

1003-9511(2016)05-0060-04

2016-04-23 编辑：胡新宇)