有限差分强度折减法与边坡安全系数和滑动面研究
2016-11-18李自扬
李自扬
有限差分强度折减法与边坡安全系数和滑动面研究
李自扬
(四川省地质工程勘察院,成都 610072)
确定安全系数和潜在滑动面是边坡稳定性分析的两项重要内容,对其的研究主要有极限平衡法和强度折减法。极限平衡法由于能方便快捷搜索计算出所有潜在滑动面的安全系数而得到广泛应用;而基于强度折减法的数值模拟却能展现出边坡在应力、应变、塑性区等方面更多信息,也越来越受到重视而进行了大量相关研究。基于有限差分强度折减法是确定边坡安全系数和滑动面的一种新方法。通过简单均质边坡算例和实际复杂成层露天矿边坡实例计算、对比验证,该法是科学合理且可行的,可以作为类似工作的参考。
边坡;稳定性;有限差分强度折减法;安全系数
边坡稳定性分析是边坡工程的重要内容,而其中潜在滑动面和安全系数的确定是两项关键问题。边坡稳定性分析方法主要有确定性方法和非确定性方法两大类,前者包括工程地质法、模型试验法、极限平衡法、极限分析法、数值模拟法以及可靠度分析法等,而后者是指各种以概率统计理论为基础发展起来的模糊随机分析方法。实际工程实践中最常用的是极限平衡法与数值模拟法。
极限平衡法,即极限平衡条分发为当前最广泛使用的边坡稳定性分析方法,同时也被纳入我国边坡规范之中。但其也主要有以下两点不足:不同的条分发法都或多或少存在条块间受力的假设并简化以及有的并不完全同时满足力和力矩的平衡;另外其本质是一种刚体力学,不能反映边坡的变形和应力应变等力学状态。
数值模拟法,是近代由于计算技术的发迅速发展兴起的方法。数值模拟法专注岩土领域的FLAC有限差分法;以及近来年迅速兴起,在细微观力学机理研究方面表现其突出优势的离散单元法等。数值模拟法能够有效克服极限平衡法的两点不足,广泛应用于研究弹塑性、动力非线性、多相耦合等基础科研问题。但掣肘于计算软硬件而需要大量计算时间,有待于进一步发展。
极限平衡法由于其力学机理明确及计算过程快而有极大优势。很多商业软件都能快速搜索出具体二维边坡包括最危险滑动面在内的所有潜在滑动面以及整个边坡剖面安全系数云图,能给工程人员提供比较清晰而科学的参考。同时为克服常规搜索滑动面方法的不足,众多学者在基于遗传算法[1]、模拟退火算法[2]、自适应蚁群算法[3]、动态规划法[4]、混沌优化法以及多种方法结合的联合搜索法等滑动面搜索方法[5]方面进行了研究应用并取得了良好效果。然而传统的极限平衡法不足之处主要体现在其首先假设滑动面,然后计算出其安全系数,这样的结果可能与实际情况存在较大出入。
相比之下,数值模拟法,在这方面就表现略逊一筹。主要是诸多数值方法虽然能给出边坡力学状态等方面详细信息但是基于此法的边坡破坏判据尚不能统一,此外有的软件虽然能够基于强度折减法自动搜索求解出边坡最小安全系数,若结合其它如剪应变、位移云图也能够比较准确确定最危险滑动面范围。而实际工程中,不仅仅是最危险滑动面,其安全系数相近的较危险的滑动面范围也具有重大现实意义而应该被明确[6],即最好能给出关心区域的安全系数云图。但同时基于强度折减的数值模拟法也有其独特优势:能根据剪应变、应变增量等与实际破坏形式符合的状态量自动确定危险滑动面。
本文将基于有限差分强度折减法的动态求解过程,初探确定边坡潜在滑动面和安全系数的新方法。
1 基本原理和方法
1.1 有限差分强度折减法原理
FLAC3D,即三维连续介质快速拉格朗日分析法,是一种广泛应用于岩土工程领域的显示差分程序。其核心包括离散模型、有限差分和动态松弛三部分,最适用于非线性、大变形及物理不稳定性等病态系统。通过FLAC3D分析问题的过程,可以看出,基于虚功原理、由应力和外力并利用动力方程分析求解静力问题是其显著特征。虽然计算过程中会产生较大节点不平衡力和速率,实际上一个合理安全的模型,其最终两者都会趋向于一个相对极小的值,即模型最终处于“伪静态”平衡的静力平衡状态[7]。
FLAC3D内置的基于强度折减法求解安全系数命令SOLVE FOS的过程不同于有限元的迭代法,FLAC采用的是一种动力的时步推进模拟法,因而除了能模拟出稳定的平衡状态之外还有连续运动状态,即现实中的不稳定状态。这样内置的SOLVE FOS流程总能得出一个安全系数的有效解。该法最大的优点就是过程完全自动化,只需要一句命令即可得出一个全局最小安全系数,并已被证明在网格划分满足精度要求的时候,其值是较为准确可信的。
该方法存在两方面不足:一是耗时,对于稍复杂的模型少则几小时,多则需要几天时间,实际工程运用则更难;二是计算结果是全局最小安全系数,而实际整个边坡中我们关心范围的安全系数分布状况。对于前者,主要是由于程序搜索安全系数范围大、精度高(0.005),从而导致r(模型特征反应时步,即模型应力状态得到一定扰动过后,重新计算恢复到初始状态所需要的时步数)较大,而且循环次数较多。对此,众多研究者偏向于自拟FISH语言控制程序进行计算,这样效率可以得到大大的提高,但遗憾的是少见就程序控制中相关关键参数和机理能作进一步详细解释的文献资料。对于后者,直接的解决方法就是求出边坡的安全系数云图,但相关研究文献更是很少、很难见到。
1.2 边坡失稳判据
数值模拟法所采用的本构方程会包含明确的屈服准则,工程实际中有的为安全起见,可以暂且保守认为屈服是不允许的,即若最终进入塑性状态就认为该处岩土体破坏,但是关于整个边坡是否会发生失稳破坏还需要进一步研究。虽然目前基于数值模拟法的边坡失稳判据虽然尚未统一,但归纳起来主要有三类,即计算收敛判据,位移判据和塑性区判据。
众多学者基于有限元法进行了大量相应研究。赵尚毅、郑颖人[8]认为:塑性区从坡脚到坡顶贯通并不一定意味着边坡破坏,其实必要条件,而不是充分条件。还需要看其是否有限制其进一步塑性流动的边界条件,并结合计算是否收敛、平衡方程是否有解进行判断。裴利剑等[9]认为:在网格精度比较合理时,三类边坡失稳判据具有一致性和统一性,且迭代不收敛判据使用最为方便并真实可靠。陈力华、靳晓光[10]认为:对一般边坡三种判据有较好的一致性,陡边坡三种判据存在较大的差异,另外同时考虑张拉、剪切破坏的强度折减法在边坡稳定性计算中才具有普遍的适用性。
其实边坡的失稳是一个复杂的过程,其力学机理等尚存在一些不明之处。综合对比分析,可以发现三类失稳判据宏观原理上存在统一性,然而又在微观精度上有一定的局限性。因此有必要进行具体问题,综合分析,确定一个适应于具体工程的判据。夏世友[11]等认为联合塑性区贯通和速度矢量图可以较好判断边坡的实际状态。本文将在此基础上,结合算例和工程实际进行相关条件和参数进行进一步研究。
1.3 主要流程
结合FLAC3D一般分析流程、SOLVE FOS自动求解最小安全系数过程,本文的研究包含边坡潜在危险滑裂面和安全系数的安全系数云图求解新方法。
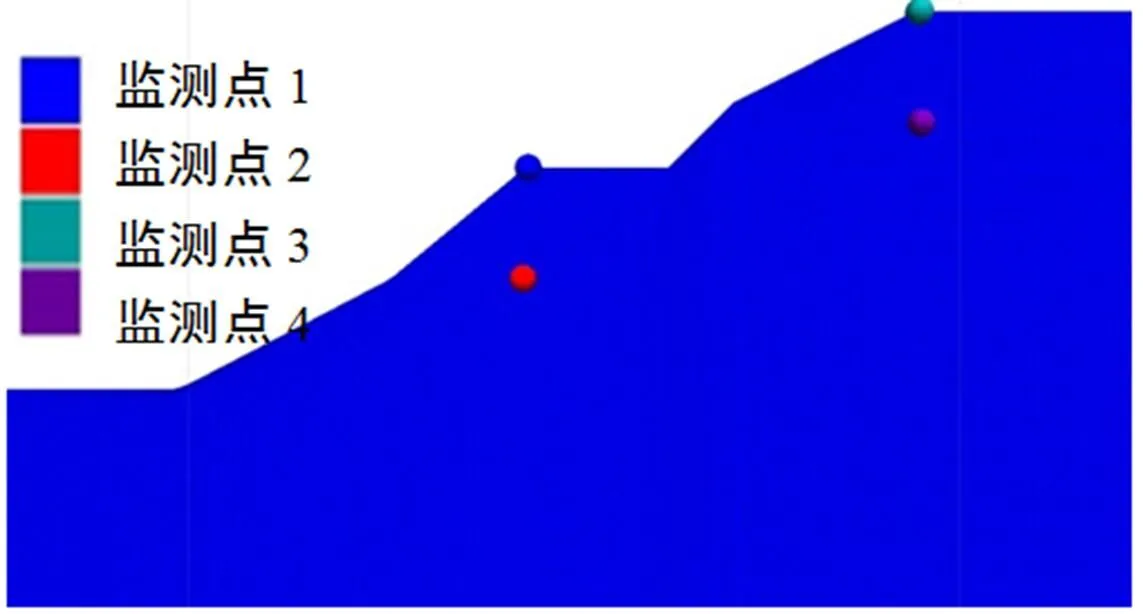
图1 算例模型及监测点位置
该过程中特别引入了前期的检验环节,可以通过FLAC3D的SOLVE FOS有限差分强度折减法和极限平衡法的计算结果对比进行,以确保FLAC3D模型在网格精度(网格大小及网格分布)、材料参数等方面基本满足要求。接下来的重要环节,就是根据SOLVE FOS的计算结果确定相关参数(N、F、v),然后根据所关心的安全系数范围,确定F,基础之上再确定精度(安全系数云图中的增量)。其中节点变量用以每次更新赋值那些v>v(即介质处于持续运动状态、处于不平衡的“失稳”状态)的节点,最终以该变量作出节点云图,即可理解为安全系数云图。需要注意的是最终未能达到v的所有节点变量都赋值F并无实际意义,只是为了最终云图表达更加清晰,以便进一步研究。
2 算例验证
2.1 验算模型与方案
首先在多台阶复合均质土坡中进行算例验证。为研究折减过程中模型状态变化,对如图示4个特征点进行速度和位移监测。对比SOLVE FOS和极限平衡法计算结果,表明两者安全系数相近(SOLVE FOS求解结果为1.312,相差<0.05),结合节点速度云图也可以发现最危险滑动面也非常吻合,综合表明该模型满足要求。结合SOLVE FOS结果确定相关计算参数(见表1)。为研究相关参数敏感性影响,拟定验算方案(表1)。如果边坡已经失稳(模型计算结果处于持续运动状态),可以预见随时计算步数的增加,速度(位移)会持续增加,所以只要两者相匹配即可使所得的结果满足要求。为研究是否存在局部不稳定现象,安全系数范围取为1.1~1.6,精度(增量)为0.05。
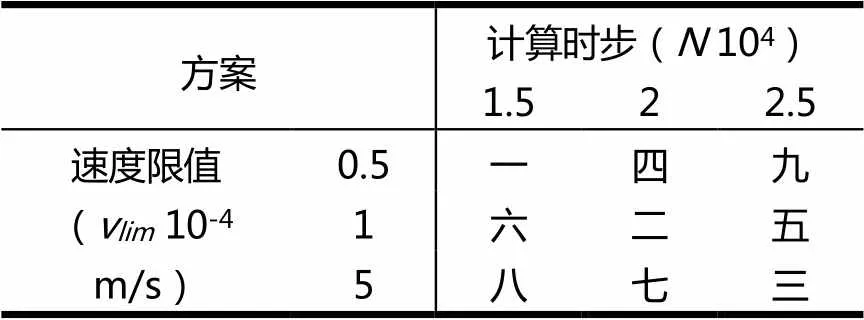
表1 验算方案设计
2.2 验算结果
按照计算流程,对表2所示计算方案进行试算。由关键点监测结果可以看出:

表2 岩土物理力学参数表
折减系数增加到1.35时边坡才开始出现持续运动的“失稳”现象,说明安全系数在1.3~1.35之间,计算数值和滑面位置都与极限平衡法的结果吻合较好;可见基于SOLVE FOS所得结果确定的相关计算关键参数敏感性较低,可以直观确定;速率判据与特征点位移突变规律相一致,具有现实参考意义;单台阶破坏时滑动面是近似圆弧形,而多台阶复合破坏时,滑动面可能会出现折线形态。
为了进一步研究新方法所得的潜在滑动面和安全系数的合理性,特利用传统极限平衡法(圆弧滑动面、简化Bishop法)计算出对应典型画面的安全系数及其分布范围。通过对比结果说明了直接基于SOLVE FOS计算结果确定参数的科学合理性;新方法可以找到安全系数约为1.4的潜在的折线滑动面,相比全部圆弧滑面更具广泛现实意义;新方法在均质土坡中是科学合理并可行的。

图2 计算结果
(a.有限差分强度折减法安全系数云图;b.有限差分强度折减法最终塑性区分布图;c.极限平衡法安全系数在2.3以下所有滑动面及有限差分对应可能滑面的安全系数)
3 工程实例
工程实例来自于某露天矿边坡,剖面地层信息见图7所示,材料参数见表2。模型长×高为800m×400m,其中边坡高220m;地层成层分布,包含多组岩土体,地质条件十分复杂。
自从基建期以来,该区上部软土层(粉土、粉质粘土)已先后发生了两次较大规模滑坡。经过削坡处理,软弱层整体坡脚已降到20°以下,至此才确保边坡现状的基本稳定。然而经过钻探发现下部仍存在软弱层带(破碎风化带),该区边坡稳定性还需进一步研究。
依据前文提出的思路和方法,对该剖面进行实例分析计算,由结果可以看出:
最小安全系数约为1.3,破坏区域位于软弱层(破碎风化带)分布高程范围内,跨越两个行车宽平台;当折减系数达到2.1以上时,整个边坡跨度范围都出现了不稳定现象,图2-a和图2-b的范围对应,说明速度达到限值、节点处于持续运动状态时,边坡也进入了塑形流动状态;结合图2-a和图2-c可以看出图2-a所确定的安全系数云图比较合理;相比于图2-c中搜索计算出的众多潜在滑面,图2-a中计算所得的复合滑动面更为科学合理,因为边坡为成层边坡,软弱层的存在对边坡稳定性有重要影响;如图2-c所示,对于露天矿边坡工程实际,可能存在局部单台阶小范围的片帮,即安全系数很小(小余1.2),这对于露天矿是可以接受的。而从图2-a中可以看出,由于其是连续介质并考虑到了变形,所以仍能计算平衡,即安全系数大于1.3;新方法在该边坡实例中的计算结果是较为科学合理的,可以进一步研究运用。
4 结语
该文基于FLAC有限差分强度折减法初探出一种确定边坡安全系数和滑动面的新方法,并通过简单均质土坡试算以及实际工程露天矿边坡实例应用的验证,综合分析可以得出以下结论:
1)强度折减法和传统极限平衡法所得结果在一定精度条件下是一致的,证明了两种方法是相通的;
2)数值模拟分析边坡稳定性的三种判据是统一但是有先后的,实际运用中还应具体问题,具体综合对比分析;
3)新方法确定的边坡安全系数和滑动面与极限平衡法相互验证,说明新方法是科学合理的;同时通过实例计算,证明在时间效率上也是可行的。
参考文献:
[1] 弥宏亮. 遗传算法在确定边坡稳定最小安全系数中的应用[J]. 岩土工程学报,2003,25(6) : 671~675.
[2] 张浩. 边坡最危险滑动面全局搜索的模拟退火算法及改进[J]. 吉林大学学报,2007,37(1) : 129~133.
[3] 陈昌富.自适应蚁群算法及其在边坡工程中的应用[J]. 浙江大学学报,2003,37(5) : 566~569.
[4] 范鹏贤. 动态规划法求解边坡安全系数最小上限解[J]. 岩土工程学报,2007,29(3) : 467~470.
[5] 曹平. 复杂边坡滑动面确定的联合搜索法[J]. 岩石力学与工程学报,2010,29(4) : 814~821.
[6] CHENG Y M,LANSIVAARA T,WEI W B. Two-dimensional slope stability analysis by limit equilibrium and strength reduction methods [J]. Computers and Geotechnics,2007,34(3):137~150.
[7] Itasca Consulting Group. FLAC3D(Fast Lagrangian Analysis of Continua in 3 Dimensions) Mannual . 2008.
[8] 赵尚毅、郑颖人. 有限元强度折减法在土坡与岩坡中的应用[J]. 岩石力学与工程学报,2004,23(19) : 3381~3388.
[9] 裴利剑等. 有限元强度折减法边坡失稳判据的统一性[J]. 岩土力学,2010,31(10) : 3337~3341.
[10] 陈力华、靳晓光. 有限元强度折减法中边坡三种失效判据的适用性研究[J]. 土木工程学报,2012,45(9) :136~146.
[11] 夏世友等. 有限差分强度折减法求解边坡安全系数[J]. 武汉大学工程学报,2012,34(4) : 19~21.
Strength Reduction Finite Difference Method for Determination of the Safety Factor and Sliding Surface
LI Zi-yang
(Sichuan Institute of Geological Engineering Investigation, Chengdu 610072)
Safety factor and potential sliding surface are determined by limit equilibrium method and strength reduction method. Strength reduction finite difference method is a new method of determination of the slope safety factor and potential sliding surface. Calculation and correlation of simple homogeneous slope and complicated bedded slope indicate its rationality.
slope; safety factor; stability; strength reduction finite difference method
[P642.3]
A
1006-0995(2016)03-0431-04
10.3969/j.issn.1006-0995.2016.03.018
2015-07-27
李自扬(1982-),男,辽宁锦州人,工程师,主要从事工程地质相关工作
