基于遗传算法的二次回归方程在沉降数据处理中的应用

2016-11-18王江荣袁维红任泰明

城市道桥与防洪 2016年10期

关键词：回归方程软土序号

王江荣，赵　睿，袁维红，任泰明

（1.兰州石化职业技术学院信息处理与控制工程系，甘肃兰州730060；2.兰州石化职业技术学院土木工程系，甘肃兰州730060）

基于遗传算法的二次回归方程在沉降数据处理中的应用

王江荣1，赵睿1，袁维红2，任泰明1

（1.兰州石化职业技术学院信息处理与控制工程系，甘肃兰州730060；2.兰州石化职业技术学院土木工程系，甘肃兰州730060）

软基路基沉降与其影响因素之间呈非线性关系。以某软基高速公路为例，以时段天数、时段载荷量及时段加载平均速率为解释变量，以时段沉降量为被解释变量，建立了非线性二次回归模型，并用遗传算法估算模型系数。工程实例表明，经遗传算法优化的非线性二次回归方程具有较高的预测精度，效果优于神经网络，用该模型进行软基高速公路沉降预测分析是可行的。

路基沉降；二次回归方程；神经网络；遗传算法；预测分析

0　引言

在软土地基上修建高速公路面临的主要问题是如何有效控制路基沉降。由于软土地质坚固性低、压缩性大、透水性差，一旦发生变形，往往持续时间较长，这些特点给高速公路建设造成一定困难。较为准确地预测软基沉降是保证施工质量、有效控制沉降变形的关键。寻求可操作性强、精确度高、有较强数据适应能力的沉降预测方法是工程技术人员长期的追求。因为软土路基沉降是一个复杂的非线性系统，其影响因素较多[1-3]，其中可量化、易于采集且对路基沉降有重要影响的因素有填土时间、载荷量及加载速率等。对于这类多因素非线性系统的数据处理许多研究者采用了人工神经网络方法[4-7]，并取得了不错的效果。但人工神经网络存在模型结构复杂、运算量大、运算结果不稳定和预测精度不高的问题。另外，神经网络对样本数据的数量及质量要求较高，且容易发生过拟合现象。基于此，本文给出另一种沉降数据处理方法——二次回归分析法，并对其中的模型参数采用遗传算法求解。工程实例分析表明，基于遗传算法的二次回归方程具有较高的精确度和可靠性，沉降预测效果优于神经网络，而且模型结构简单、变量间的依赖关系清晰、实际操作方便，用以软基路基沉降预测是可行的。

1　基础数据

文献 [8]介绍了某软基高速公路的工程概况（在此略去）,并以时段沉降量为目标观测值y （mm)，以时段天数t（d)、时段载荷量[时段填土高度P(m)]和时段填土速率ΔP(m/d)为指标观测值（属性值），经过约13个月观测得到了25组观测数据，见表1。

以表1中序号1～20的数据建模，并用序号21～25的数据检测模型。

2　模型建立

设x1=时段天数（d），x2=时段填土高度（m),x3=时段填土速率（m/d）,y=时段沉降量（mm）。则y关于x1、x2及x3的完全二次回归方程为

式中：b0、b1、b2、b3、b12、b13、b23、b11、b22、b33为回归系数。采用遗传算法来估算这些回归系数。

表1　沉降观测数据表

在MATLAB工作窗口利用gatool命令打开遗传算法的GUI[9],在Fitness function窗口输入@finess，在Number of variables窗口输入待估参数个数10，在边界约束Lower输入[3.95,-5.71,329.66,-3452.68, -20.52,137.13,-24002.64,-4.98,822.78,170349.03], 在Upper输入 [13.95,4.29,339.66,-3442.68,-10.52, 147.13,-23992.64,5.02,832.78,170359.03],种群规模为80，迭代次数为4 000，其他参数选用缺省值，然后单击Start按钮执行遗传算法，得出的适应度函数的变化过程如图1所示。

图1适应度函数变化曲线

迭代2 000余次后终止，输出的参数值（四舍五入）为：b0=3.949 6，b1=-0.028 2，b2=332.202 3，b3= -3 442.681 8，b12=-15.268 5，b13=139.491 3，b23=-23 992.643 9，b11=-0.002 3，b22=829.538 3，b33= 170 359.029 2。将这些参数值代入模型（1）得到的二次回归方程为

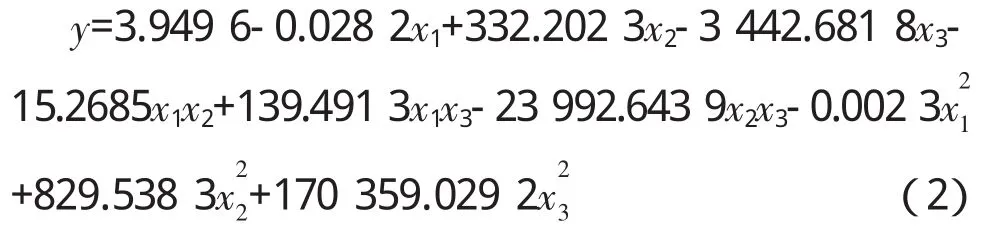
回归方程的显著性检验：决定系数R2=0.931 1,方均误差MSE=0.437 5。可见回归方程的拟合效果是显著的，可以用于软基路基沉降的后期预测。

3　模型检验

3.1模型预测精度分析

将测试样本（表1中序号21～25的数据）的指标值即时段天数、时段填土高度和时段填土速率代入回归方程（2）得出的时段沉降预测值见表2。作为比较，在相同样建模样本与测试样本条件下，将文献[8]中的神经网络（网络训练样本集由表1序号1～20数据构成，测试样本为表1中序号21～25的数据）的预测结果和用逐步回归法[确定方程（1）的模型系数，建模样本为表1中序号1～20的数据，检验样本为表1中序号21-25的数据]得出的预测结果置入表2中。

从表2给出的平均绝对误差和平均相对误差来看，本文建立的预测模型具有较高的精确度，预测结果整体好于文献[8]给出的神经网络的预测结果，也好于基于逐步回归算法的二次回归方程的预测结果。与神经网络相比，本文模型最大的优点在于模型结构简单，可操作性强，计算结果稳定，且对样本数据无过多要求，用于指导高速公路建设是可行的。

表2　测试数据的预测结果及分析比较

3.2模型可靠性分析

为了验证模型的可靠性，将建模样本数减少为15个，即利用表1中序号1～15的数据作为建模样本，仍用序号21～25的数据来检验模型的预测精度。利用遗传算法得出的模型系数和二次回归方程为

测试样本（表1中序号21～25的数据）的指标值即时段天数、时段填土高度和时段填土速率代入回归方程（3）得出的时段沉降预测值见表3。

表3　基于15个建模样本的三个模型的预测结果

从表3可看出，在减少建模样本后三种模型的预测精度有不同程度的下降，尤其神经网络的预测精度有了较大幅度的降低，已不能满足工程需要；而本文模型及逐步回归二次回归方程的预测精度降幅很小，而以本文模型预测精度降幅最小（非常接近原预测精度），能够满足工程需要。表明在减少建模样本时本文模型的稳定性和可靠性较高，受其影响较小，而对神经网络的预测精度影响较大。从另一方面说明神经网络对建模样本数量有较高的要求，只有训练样本数足够多时才能取得理想的预测精度。