几个荧光蛋白发色团双光子吸收性质的理论研究

叶传香马会利梁万珍

（1中国科学技术大学化学物理系，合肥 230026；2清华大学化学系，北京 100084；3厦门大学化学系，福建 厦门 361005）

几个荧光蛋白发色团双光子吸收性质的理论研究

叶传香1马会利2梁万珍3,*

（1中国科学技术大学化学物理系，合肥 230026；2清华大学化学系，北京 100084；3厦门大学化学系，福建 厦门 361005）

实验测得的荧光蛋白的单、双光子吸收光谱在低频和高频区域都表现出明显不同的特征。为了揭示这些不同点的起源和研究荧光蛋白的构–效关系，我们详细研究了三种荧光蛋白发色团（一种增强型蓝绿色荧光蛋白的中性发色团和两种红色荧光蛋白的阴离子发色团）的单、双光子吸收特性，分别计算了纯的和振动分辨的电子谱。计算结果表明：光谱线形与计算采用的交换相关密度泛函及谱截面计算所采用的近似关系密切；如果在计算光谱截面时，我们利用长程修正的交换相关泛函CAM-B3LYP来计算几何和电子结构参数，然后把Franck-Condon （FC）效应和包含Herzberg-Teller （HT）效果的电-声耦合效应都考虑进去，理论计算的光谱与实验测定的光谱可以很好地符合；对于两种离子态的发色团，HT电-声耦合效应使得对应于基态到第一激发态跃迁的双光子吸收最强峰相对于单光子吸收的最强峰发生了蓝移，但HT电-声耦合效应对高频的双光子吸收谱没有太大的影响；分子内电荷转移是导致高频区的双光子吸收明显强于单光子吸收的主要原因。

双光子吸收；荧光蛋白发色团；振动光谱；含时密度泛函理论

1 Introduction

In recent years, the two-photon absorption （TPA） phenomena of fluorescent proteins （FPs） have attracted a lot of interests1–5. The main reason is that the TPA spectra of FPs have fascinating applications in bioimaging and medical technology as biomarker, biosensor6,7, and now even in communication technology8. Especially, FPs are widely used in two-photon laser scanning microscopy, which can penetrate deeper tissue with less damage9. Therefore, the scientists have performed a large amount of experimental studies to investigate which proteins are the brightest and what are the best excitation wavelengths. However, due to competing optical processes such as stimulated emission and scattering that arise in high-intensity regime inherent in these experiments, it is difficult to experimentally measure the absolute TPA cross sections10. In biological systems, there are additional calibration difficulties leading to significant discrepancies in the reported measurements of absolute TPA cross sections2. It is thus essential to theoretically calculate the TPA cross sections to assist experimental studies for describing the microscopic excited-state dynamics, explaining the experimental results and designing new materials with desired non-linear optical properties as well11.

Numerous computational studies of TPA phenomena have been reported in the past couple of decades within the framework of time-dependent density functional theory （TDDFT）12–20, a lower-level couple cluster method21or the equationof-motion coupled-cluster method11. However, most of theoretical works were focused on the calculations of pure electronic spectra. The vibrational motions and the vibronic coupling effect are not incorporated into the spectra. Compared with the pure electronic spectra, vibrationally-resolved electronic spectra show the detailed characteristic of molecular vibrational motions and reveal more reliable molecular structure–property relationship. In this work, we thus simulate the vibrationally-resolved OPA （VROPA） and TPA （VRTPA） spectra of a few FP chromophores to obtain the fundamental structure–property relationships, unveil the origin of the significant discrepancies between OPA and TPA spectra, and reach a close comparison with the experimental spectra.

From the theoretical point of view, TPA is a non-linear optical process with a quadratic dependence of the absorption strength on the intensity of the incident light. Since two-photon transitions become allowed only in the second order of perturbation theory, TPA cross sections are usually much small. However, in TPA spectra of FP chromophores2, it is observed that the TPA spectra in high-frequency region are stronger than that in low-frequency region, while the OPA spectra are extremely weak2. It is thus urge to know the intrinsic physical mechanism which is called quantum mechanical effect known as resonant enhancement by some researchers22. We here conduct a theoretical calculation of both the TPA and OPA spectra for a few FP chromophores. The time-dependent approaches to model OPA and TPA cross sections with inclusion of Franck-Condon （FC） scattering and Herzberg-Teller （HT） vibronic coupling effects will be used23,24. Besides the efficient dynamic method, the accurate structure parameters are further needed to predict OPA and TPA cross sections. In the electronic structure calculations, the ground-state properties can be easily obtained, and the main difficulty is to provide a good description on the resonant excited-state potential energy surfaces. In principle, high-accuracy wavefunction-based correlated ab initio methods can provide an accurate description of excited electronic states. However, these techniques are currently computationally intractable when applied to molecules of practical interests. Alternatively, time-dependent density functional theory（TDDFT） approach has been proposed to calculate the excitedstate properties. The successful realization of the analytical excited-state Hessian within the framework of TDDFT25–29has made the large-scale numerical calculations feasible on the excited-state vibrational frequencies and other related physical quantities, such as the geometrical derivatives of the transition dipole moment for the medium-sized systems.

Three model FP chromophores in gas phase and water solution are investigated, which include a neutral chromophore in photoactive enhanced cyan fluorescent protein （ECFP）30and two anionic FP chromophores in DsRed2 and TagRFP31. As a result, the environment-dependent characteristics of OPA and TPA spectra of those model chromophores are exhibited. As the representation of neutral chromophore, ECFP shows an apparent overlap between the OPA spectra and TPA spectra in the longest-wavelength absorption band, corresponding to the electronic transition from the ground state （S0） to the first singlet excited state （S1）. However, as the representation of anionic chromophores, Dsred2 and TagRFP show a distinct blue-shift of the low-energy TPA maxima relative to the OPA maxima. However, in higher-frequency regions, the OPA and TPA spectra of two-types of FP chromophores exhibit similar characteristics. The TPA is very strong while the OPA is extremely weak. Those strong resonant enhancements32,33appeared in TPA spectra in the short wavelength definitely have crucial relationship with the characters of higher-lying excited states34. It is thus essential to present a profound insight to address the issue.

2 Computational details

On the basis of the perturbation theory, the transition rate of one-photon （two-photon） transition from the initial stateto the final stateis proportional toHere,is the lineshape function within one-photon （two-photon） transition. Here wi, w1, and w2denote the incident photon frequencies, the onephoton and two-photon transitions are separately expressed as follows:

where μ denotes the transition dipole moments between two electronic states. e1, e2represent the direction of the corresponding transition.is the intermediate states. In Born Oppenheimer （BO） approximationandcan be separated into electronic and vibrational states aswith the energyHere EL/I/Fdenotes the energy of the corresponding electronic state anddenotes the vibrational energy.

At the microscopic level, the spectral differential cross section of OPA can be explicitly written as

and the TPA cross section （σTPA） for the two identical linearly polarized photons with the energy different from the molecular electronic excitation can be written as35–38

here, i1and i2represent the Cartesian coordinate directions x, y, z.is the fine structure constant. With the exploit of the approximation（ELIis the energy gap betweenis the vibrational energy of the corresponding vibrational states）, and the closure relation of vibrational statesthe second-hyperpolarizability becomes39

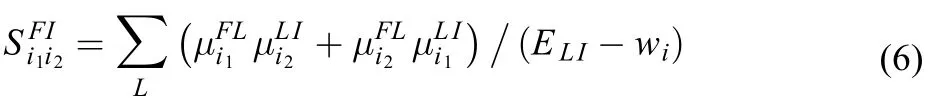
One can calculate the cross sections in Eqs.（3） and （4） by means of the sum-over-state method straightforwardly or by the time-dependent approach. The time-dependent expressions for the OPA an TPA cross sections with inclusion of Duschinsky rotation （mode-mixing）, FC and HT vibronic coupling effects have been derived in our previous works23,24,40in detail. The mode-mixing effect accounts for the differences between ground- and excited-state normal-mode coordinates and vibrational frequencies. The HT vibronic coupling effect accounts for the dependency of transition dipole moments on the mode coordinates,Therefore, to predict the OPA and TPA spectra, one is required to accurately compute the structure parameters, such as the equilibrium geometries and vibrational frequencies of resonant states, the excitation energies, the transition dipole moments, and the twophoton transition tensors as well as their geometric derivatives, etc. Even though, the ground-state properties can be easily obtained, it is difficult to calculate the excited-state properties. To avoid the difficulty, in this paper, we adopt the vertical gradient （VG） approximation41,42which has been simply described in our previous paper23,24.

In VG approximation, physically, the excited-state potential energy surface is just a mere shift relative to the ground-state potential surface without any scrambling of the normal coordinates or a change in the harmonic frequencies, i.e.,Here w denotes the vibrational frequencies and L corresponds to the transform matrix, which is obtained by the diagonalization of the mass weighted Hessian matrix H asThe displacements which are related to the structural change along the normal modeupon excitation of the molecule read

From the bank of protein data, the crystal structures of ECFP30and two red fluorescent proteins31are obtained. And then, we get the initial structures of the chromophores by rational extraction and modification. All the concerned structure parameters except the two-photon transition tensors and their geometrical derivatives are calculated by DFT or TD-DFT methods within the Gaussian 09 software package43. The twophoton transition tensors and their geometric derivatives are evaluated within the Dalton programme44. The finite-difference methods are applied to calculate the geometric derivatives of transition dipole moments and two-photon transition tensors. The hybrid DFT exchange-correlation （XC） functional B3LYP and the long-range-corrected DFT XC functional CAM-B3LYP are adopted. The basis sets 6-31G* and 6-311+G** are applied. The effect from the surrounding protein environment on molecular geometries and on spectroscopic properties has been inspected by the integral equation formalism polarizable continuum media model （PCM）45,46.

To understand the nature of electronic excitations, we analyse the excited states by constructing the natural transition orbitals （NTOs）47within the Gaussian program package. The NTOs are defined by transformations of the occupied and unoccupied molecular orbitals via the matrices U and V obtained by singular value decomposition of the transition density matrix T, i.e.,respectively. The matrices U and V are unitary and λ is diagonal.

3 Results and discussion

In order to unveil the structure–property relationship, and reveal the impacts of molecular external environments and DFT XC functional on the electronic structure and optical properties of FPs, we here investigate three model FP chromophores: the neutral ECFP chromophore, the anionic DsRed2 and TagRFP chromophores in different molecular environments. The structure parameters which enter the expressions of spectral cross sections are calculated by DFT or TD-DFT with XC functional B3LYP and CAM-B3LYP. From the bank of protein data, the crystal structures of concerned FPs are obtained, and then, we get the initial structures of the chromophores by rational extraction and modification.

3.1 Neutral ECFP chromophore

Fig.1（a） shows the geometry of ECFP chromophore. At the optimized geometry of S0, we calculate the vertical excitation energies and corresponding oscillator strengths of OPA and TPA as shown in Table 1. Then, both the pure electronic and vibronic spectra are simulated. Here we only show the low-frequency OPA spectra since the OPA transition is forbidden in the high-frequency region as Table 1 shows. The experimental TPA spectrum of ECFP, in Fig.1（b）, shows three TPA bands centered at around 857, 640, and 550 nm with different spectral intensities. The theoretical spectra, in Fig.1（c–f）, are calculated with respect to the geometric and electronic structure parameters produced by different DFT XC functionals at different molecular environments. It is found that the calculated OPA and TPA peaks by TD-B3LYP/PCM coincide rather well with the experimental spectra in the long wavelength region. Obviously, TD-CAM-B3LYP overestimates the excitation energies and subsequently blue-shifts the spectra compared with the experimental measurement. The solvent effect decreases the excitation energies. From the calculated pure electronic spectra ofTPA （the blue lines in Fig.1）, we observe that the relative order of peak intensities of TPA spectra calculated with respect to structure parameters by TD-CAM-B3LYP/PCM is almost consistent with the experimental TPA spectrum if we redshift the pure electronic TPA spectrum about 100 nm. However, it is obvious that the spectral width cannot be well produced by the simply broadening by means of the line-shape function. We thus calculate the vibronic spectra at different approximations. It is obvious that the calculated vibronic spectra with inclusion of FC and HT effects provide us more abundant information about vibrations and vibronic coupling, which actually matches the experimental spectral lineshape quite well. For example, in the long wavelength region, the first absorption band corresponds to the electronic transition of S0→ S1and both OPA and TPA show a board band width of about 200 nm. Our simulation verifies that the boarding comes from the vibrational transitions between different electronic states. The second TPA band centered at 650 nm corresponds to the electronic transitions of S0→ S3and S4, and the third intensive band centered at around 550 nm comes from the absorption from S0→ S5or higher energy excited electronic states.

Fig.1 Calculated and experimental spectra of ECFP chromophore in gas phase and water solution based on the structure parameters produced by B3LYP and CAM-B3LYP with the basis set 6-31G*

In addition, for ECFP chromophore, we observe that no obvious blue-shift phenomenon appears at TPA maximum of the neutral ECFP chromophore and the spectra under FC andFCHT approximations are nearly same, which indicates that the HT vibronic coupling does not have large contribution to the vibronic spectra of low-frequency band. The calculated TPA spectra with VG approximation and without VG approximation show slight differences, especially the peak intensities （see Fig.1（c, d））, which indicates that to correctly predict the VRTPA spectra, it seems important to include the difference of the potential energy surfaces between the resonant states. Due to the expensive computational cost of the excited-state Hessian calculation, in the later calculations, we thus adopt VG approximation.

Moreover, to further understand the nature of the excited states, we make an analysis on the NTOs corresponding to electronic transitions from the ground state to the low-lying singlet excited states for ECFP chromophore in water solution. Comparing the hole/particle NTO pairs for the transitions corresponding to three low-lying excited states as shown in Fig.2, we observe the obviously photon-induced intramolecular chargetransfer CT character in the later two excitations, while the intramolecular CT character companying with the first excited state is not visible. The character of excited states indeed explains why OPA is allowed for the transition of S0→ S1, but it is forbidden for the transitions from S0to higher excited states, and it also explains why CAM-B3LYP can yield the correct order of excited states and better TPA spectral lineshapes compared with the experiments although it overestimates the excitation energies.

Fig.2 Electronic densities of hole and particle NTO pairs with largest values of λ for the dipole-allowed singlet excited states of ECFP chromophore

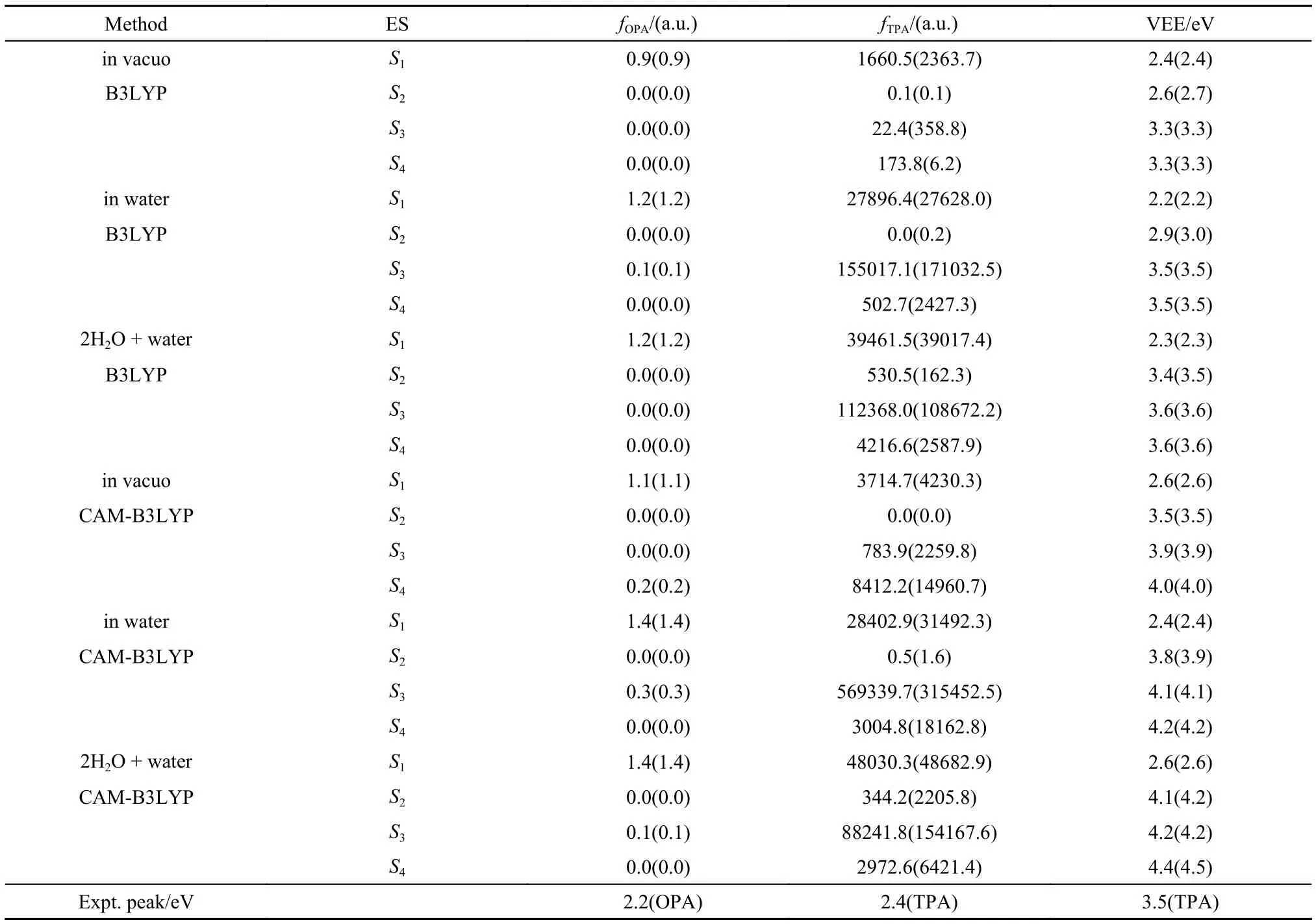
Table 2 Basic parameters of DsRed2

3.2 Anionic DsRed2 chromophore

Then we calculate the anionic DsRed2 chromophore48with the same procedure for the neutral ECFP chromophore. The calculated electronic structure parameters are listed in Table 2,and the calculated and experimental TPA spectra of DsRed2 chromophores are shown in Fig.3（b–f）.

By inspecting into Fig.3（a）, it is easily found that the experimental TPA maxima are centered at 700 and 1050 nm, while the low-energy OPA maximum is centered at 1100 nm. Obviously, the first TPA maximum has a blue-shift of 50 nm relative to the OPA maximum. Comparing the theoretical spectra calculated at different levels as shown in Fig.3（b–f）, TDB3LYP/PCM produces best consistent peak positions with the experimental profiles. The VRTPA spectrum based on the structure parameters produced by B3LYP/PCM gives two evident TPA bands whose main peaks are located at 712 and 1120 nm and VROPA spectrum shows one main band located at 1138 nm. Obviously, the blue-shift value between the first main TPA and OPA maxima are not exactly yielded by the vibronic spectra calculated with respect to the structure parameters from B3LYP/PCM. The calculated vibronic spectra with respect to the structure parameters from CAM-B3LYP/PCM show the exact value of experimentally-measured blue-shift. The HT vibronic coupling effect is extremely significant on TPA spectra of the DsRed2 anionic chromophore in the low-frequency region, which results in the blue-shift of the first TPA maximum relative to OPA maximum.

Fig.3 Calculated and experimental spectra of anionic DsRed2 chromophore in gas phase and water solution

To well analyze the TPA spectra, the pure electronic TPA spectra are simulated, too. The correct relative intensities of absorption bands are produced by the pure electronic spectra. In Fig.3（d）, we also show the result （the green line） with a different molecular geometry which is obtained by optimizing theneutral chromophore and discarding a proton from the optimized geometry without further optimization. With this geometry, the calculated relative intensities and locations of TPA peaks agree better with the experimental measurement. It is obvious that the resonant forms of geometric structure determine the properties of anionic chromophore.

Fig.4 Electronic densities of hole and particle NTO pairs with largest values of λ for the dipole-allowed singlet excited states of DsRed2 chromophore in solution （a） and the complex formed by 2H2O and DsRed2 chromophore （b）

Combining vibronic spectrum and pure electronic spectrum, we assign the first band in the experimental spectrum coming from the electronic transition of S0→ S1. As for the second band, it may come from the contribution of two electronic transitions because the third and fourth excited states are nearly degenerate. From Fig.3（d）, the transition of S0→ S3makes dominant contribution to the second band and the contribution from the transition of S0→ S4is small.

Table 3 Basic parameters of TagRFP

As we all know, the experimental TPA spectra of those chromophores are acquired under the protein environment, which includes water molecules, counter ions, nearby charges, or polar amino acids. Therefore it is necessary to take the perturbation of protein environment to the photoactive part into considerations. To simplify the calculations, in the above work we just focus on the solvent effect. The implicit solvent PCM has been applied for the single chromophores. Here we consider complexes which are formed by the anionic chromophores with twoexplicit solvent water molecules. Then the hydrogen-bond complexes are calculated at the theoretical level of B3LYP/PCM. Two water molecules are put around the phenyl ring of the chromophores to form double hydrogen bonds with the anionic oxygen atom28,49. Compared with the results of the anionic DsRed2 chromophore without explicit solvent molecules, the vertical excitation energy of the first excited state increases 0.1 eV and the energy spacing between the third excited state and the fourth excited state still keeps relatively small. With the smaller energy space, the coupling between the third and the fourth excited states may play an important role in the TPA spectrum. As we observe from Fig.3（b, d）, the calculated TPA spectra show distinct difference on the higher energy region and the first absorption bands are not influenced much except the peak locations. Additionally, in Fig.4, we can not only observe the same intramolecular CT in the higher excited states with ECFP but also find visible intermolecular CT in the higher excited states when the two water molecules are taken into account. It reveals that the charge transfer phenomena occurring in the higher excited states make great contribution to the enhancement of the intensities of the TPA peaks at the high-frequency domain.

Fig.5 Calculated and experimental spectra of anionic TagRFP chromophore in gas phase and water solution

3.3 Anionic TagRFP chromophore

Finally, we move to anionic TagRFP chromophore50. The cal-culated electronic structure parameters are listed in Table 3. The experimental spectra in Fig.5（a） show three low-energy TPA bands centered at around 600, 759, and 1100 nm and two OPA bands centered at around 700 and 1100 nm. The lowest-energy TPA and OPA bands centered at 1100 nm correspond to electronic transition of S0→ S1. Overall, the calculated vibronic spectral lineshapes based on the structure parameters produced by CAM-B3LYP/PCM coincide with the experimental data although the peak positions are overestimated. Like anionic DsRed2 chromophore, a distinct blue-shift can be found between the TPA maximum and OPA maximum within the first absorption band, which is ascribed to HT vibronic coupling effect. However, HT effect is not so evident in the high-energy region since there is no large discrepancy between the pure electronic spectrum with the spectral boarding and the vibronic spectrum, and the calculated spectral lineshapes are almost same with the experimental one. The second TPA band corresponds to the electronic transition of S0→ S3and the third TPA band at around 600 nm comes from the electronic transition from the ground state to higher excited electronic states. For B3LYP/PCM, the dominant contribution to the third band is from the electronic transition of S0→ S8while for CAMB3LYP/PCM, the dominant contribution is from the electronic transition of S0→ S5. Like DsRed2 chromophore, the same CT character can be found from Fig.6 for TagRFP and again strengthens the significance of it in the enhancement of the TPA peaks corresponding to the higher excited states. Additionally, comparing the structures of two anionic chromophores, it is easily found that the DsRed2 chromophore is cis conformation, while the TagRFP chromophore is trans conformation51–53. Even though they have same atom composition, their TPA spectra show different characters mainly ascribing to the difference of their geometric structures. Our calculations demonstrate that the conformation of a chromophore affects its TPA spectrum to some extent.

Table 4 Calculated transition dipole moments between the different states at the different theoretical levels

Fig.6 Electronic densities of hole and particle NTO pairs with largest values of λ for the dipole-allowed singlet excited states of TagRFP chromophore （a） and 2H2O + TagRFP chromophore （b）

It is noted that the transition dipole moments from S0to S1（μ01） and from S1to Sn（n > 1） can also do us a favor to understand the nature of resonant enhancement of TPA corresponding to the electronic transition from S0to the high-lying excited states. The transition dipole moments of three FP chromophores have calculated and shown in Table 4, which have been calculated by B3LYP/PCM since B3LYP can reproduce more consistent experimental peak locations. From our calculations we know the transitions from S0to Sn（n > 1） are weak and some transitions from S1to Sn（n > 1） are strong. The transition dipole moments from S1and Sn（n > 1） actually play a key role in deciding the intensities of TPA peaks in high-frequency domain since in the three-level approximation, the TPA cross section can be written asFor ECFP chromophore, the ratio ofcan directly predict the relative intensities of TPA peaks in low-frequency domain. For DsRed2 and TagRFP, the ratio of μ01: μ13can also give the right relative intensities in TPA.

4 Conclusions

In this work, we have investigated the OPA and TPA proper-ties of three FP chromophores in gas phase and water solution

. Both the pure electronic and vibrationally-resolved electronic spectra have been calculated. We focus not only on the lowestenergy excited state but also on the transition from the ground state to the high-lying excited states. Comparing the calculated and measured spectra, all the absorption peaks are analyzed and characterized. The transitions occurring at different wavelengths make different contribution to the TPA peaks which are illuminated qualitatively. The corresponding electronic excitations have been characterized by the hole/particle pairs of natural transition orbitals. The DFT XC functional effect on the OPA and TPA spectra has been checked. In the calculations, the structure parameters which enter the spectral cross sections are obtained by DFT or TDDFT. Two functionals, B3LYP and CAM-B3LYP, have been applied.

The following conclusions have been achieved by this investigation. （1） The calculated electronic structures are functionaldependent. TD-B3LYP usually produces the excitation energies closer to the experiment while TD-CAM-B3LYP overestimates the excitation energies. However, the vibronic spectral lineshapes based on the structure parameters produced by CAM-B3LYP/PCM are more consistent with the experimental measurement even though one has to redshift the vibronic spectra 100 nm. （2） The experimental spectral lineshapes can be exactly produced by the calculated vibronic spectra with inclusion of FC and HT effects. The blue-shift phenomenon of TPA maximum in lowest-energy band for anionic chromophores is ascribed to significant HT vibronic coupling effect. However, the HT effect on the TPA spectra of high-frequency region is insignificant. （3） The high-lying excited states possess intramolecular CT character which indeed explains why TPA spectra in higher-frequency region are much stronger than the OPA spectra.

In this work, we just utilize the implicit or implicit + explicit solvent model to model the protein environmental effect which is not enough. In future work, we expect to use QM/MM method28to deal with the micro environment of the chromophore and more perturbations like counter ions, nearby charges, or polar amino acids and so on will be taken into account in order to better reproduce the experimental result and investigate the relationship between the intrinsic electronic structures and the TPA spectra. We expect that the data and information received from this theoretical work can provide a comprehensive guide for the researchers to choose the right FP and excitation wavelength for two-photon application of FPs.

（1）Zimmer, M. Chem. Rev. 2002， 102, 759. doi: 10.1021/cr010142r

（2）Drobizhev, M.； Makarov, N. S.； Tillo, S. E.； Hughes, T. E.；Rebane, A. Nat. Methods 2011， 8, 393. doi: 10.1038/nmeth.1596

（3）Drobizhev, M.； Tillo, S.； Makarov, N.； Hughes, T.； Rebane, A. J. Phys. Chem. B 2009， 113, 855. doi: 10.1021/jp8087379

（4）Spiess, E.； Bestvater, F.； Heckel-pompey, A.； Toth, K.； Hacker, M.； Stobrawa, G.； Feurer, T.； Wotzlaw, C.； Berchner-Pfannschmidt, U.； Porwol, T.； Acker, H. J. Microsc. 2005， 217, 200. doi: 10.1111/jmi.2005.217.issue-3

（5）Katan, C.； Terenziani, F.； Mongin, O.； Werts, M. H.； Porres, L.；Pons, T.； Mertz, J.； Tretiak, S.； Blanchard-Desce, M. J. Phys. Chem. A 2005， 109, 3024. doi: 10.1021/jp044193e

（6）Xu, C.； Zipfel, W.； Shear, J. B.； Williams, R. M.； Webb, W. W. Proc. Natl. Acad. Sci. U. S. A. 1996， 93, 10763. doi: 10.1073/pnas.93.20.10763

（7）Tsien, R. Y. Annu. Rev. Biochem. 1998， 67, 509. doi: 10.1146/annurev.biochem.67.1.509

（8）Hunter, S.； Kiamilev, F.； Esener, S.； Parthenopoulos, D. A.；Rentzepis, P. M. Appl. Optics 1990， 29, 2058. doi: 10.1364/AO.29.002058

（9）Chudakov, D. M.； Matz, M. V.； Lukyanov, S.； Lukyanov, K. A. Physiol. Rev. 2010， 90, 1103. doi: 10.1152/physrev.00038.2009

（10）Oulianov, D.； Tomov, I.； Dvornikov, A.； Rentzepis, P. Opt. Commun. 2001， 191, 235. doi: 10.1016/S0030-401801121-X

（11）Nanda, K. D.； Krylov, A. I. J. Chem. Phys. 2015， 142, 064118. doi: 10.1063/1.4907715

（12）Yuan, L.； Lin, W. Y.； Chen, H.； Zhu, S.； He, L. W. Angew. Chem. Int. Edit. 2013， 52, 10018. doi: 10.1002/anie.201303179

（13）Terenziani, F.； Katan, C.； Badaeva, E.； Tretiak, S.； Blanchard-Desce, M. Adv. Mater. 2008， 20, 4641. doi: 10.1002/adma.v20:24

（14）Beerepoot, M. T.； Friese, D. H.； Ruud, K. Phys. Chem. Chem. Phys. 2014， 16, 5958. doi: 10.1039/c3cp55205e

（15）Nifosí, R.； Luo, Y. J. Phys. Chem. B 2007， 111, 14043. doi: 10.1021/jp075545v

（16）Vivas, M.； Silva, D.； Misoguti, L.； Zalesny, R.； Bartkowiak, W.；Mendonca, C. R. J. Phys. Chem. A 2010， 114, 3466. doi: 10.1021/jp910010g

（17）Tretiak, S.； Chernyak, V. J. Chem. Phys. 2003， 119, 8809. doi: 10.1063/1.1614240

（18）Kamarchik, E.； Krylov, A. I. J. Chem. Phys. Lett. 2011， 2, 488. doi: 10.1021/jz101616g

（19）Steindal, A. H.； Olsen, J. M. H.； Ruud, K.； Frediani, L.；Kongsted, J. Phys. Chem. Chem. Phys. 2012， 14, 5440. doi: 10.1039/c2cp23537d

（20）Nayyar, I. H.； Masunov, A. E.； Tretiak, S. J. Phys. Chem. C 2013， 117, 18170. doi: 10.1021/jp403981d

（21）Christiansen, O.； Koch, H.； Jørgensen, P. Chem. Phys. Lett. 1995，243, 409. doi: 10.1016/0009-261400841-Q

（22）Drobizhev, M.； Makarov, N.； Hughes, T.； Rebane, A. J. Phys. Chem. B 2007， 111, 14051. doi: 10.1021/jp075879k

（23）Ma, H. L.； Zhao, Y.； Liang, W. Z. J. Chem. Phys. 2014， 140, 094107. doi: 10.1063/1.4867273

（24）Liang, W. Z.； Ma, H. L.； Zang, H.； Ye, C. X. Int. J. Quantum Chem. 2015， 115, 550. doi: 10.1002/qua.24824

（25）Liu, J.； Liang, W. Z. J. Chem. Phys. 2011， 135, 184111. doi: 10.1063/1.3659312

（26）Liu, J.； Liang, W. Z. J. Chem. Phys. 2011， 135, 014113. doi:10.1063/1.3605504

（27）Liu, J.； Liang, W. Z. J. Chem. Phys. 2013， 138, 024101. doi: 10.1063/1.4773397

（28）Zeng, Q.； Liu, J.； Liang, W. Z. J. Chem. Phys. 2014， 140, 18A506. doi: 10.1063/1.4863563

（29）Zeng, Q.； Liang, W. Z. J. Chem. Phys. 2015， 143, 134104. doi: 10.1063/1.4931734

（30）Lelimousin, M.； Noirclerc-Savoye, M.； Lazareno-Saez, C.；Paetzold, B.； Le Vot, S.； Chazal, R.； Macheboeuf, P.； Field, M. J.； Bourgeois, D.； Royant, A. Biochemistry 2009， 48, 10038. doi: 10.1021/bi901093w

（31）Pletnev, S.； Subach, F. V.； Dauter, Z.； Wlodawer, A.； Verkhusha, V. V. J. Mol. Biol. 2012， 417, 144. doi: 10.1016/j.jmb.2012.01.044

（32）Hales, J. M.； Hagan, D. J.； Van Stryland, E. W.； Schafer, K.；Morales, A.； Belfield, K. D.； Pacher, P.； Kwon, O.； Zojer, E.；Brédas, J. L. J. Chem. Phys. 2004， 121, 3152. doi: 10.1063/1.1770726

（33）Drobizhev, M.； Karotki, A.； Kruk, M.； Rebane, A. Chem. Phys. Lett. 2002， 355, 175. doi: 10.1016/S0009-261400206-3

（34）Wanko, M.； García-Risueño, P.； Rubio, A. Phys. Status Solidi-b 2012， 249, 392. doi: 10.1002/pssb.201100536

（35）McClain, W. J. Chem. Phys. 1971， 55, 2789. doi: 10.1063/1.1676494

（36）Dick, B.； Hochstrasser, R.； Trommsdorff, H. Nonlinear Optical Properties of Organic Molecules and Crystals； Chemla, D. S., Zyss, J. Eds； Academic Press: Orlando, 1987； pp 159–212.

（37）Shen, Y. R. The Principles of Nonlinear Optics, 1st ed.； Wiley-Interscience: New York, 1984； pp 216–795.

（38）Bishop, D. M.； Luis, J. M.； Kirtman, B. J. Chem. Phys. 2002，116, 9729.

（39）Silverstein, D. W.； Jensen, L. J. Chem. Phys. 2012， 136, 064111. doi: 10.1063/1.3684236

（40）Ma, H. L.Theoretical Study on the Optical Properties of Molecules and Noble Metal Nanoparticles. Ph. D. Dissertation, University of Science and Technology of China, Hefei, 2014. ［马会利. 分子与惰性金属纳米粒子光学性质的理论研究［D］. 合肥: 中国科学技术大学, 2014.］

（41）Santoro, F.； Cappelli, C.； Barone, V. J. Chem. Theory Comput. 2011， 7, 1824. doi: 10.1021/ct200054w

（42）Ferrer, F. A.； Barone, V.； Cappelli, C.； Santoro, F. J. Chem. Theory Comput. 2013， 9, 3597. doi: 10.1021/ct400197y

（43）Frisch, M. J.； Trucks, G. W.； Schlegel, H. B.； et al. Gaussian 09, Revision D.01； Gaussian Inc.: Wallingford, CT, 2009.

（44）Dalton, a Molecular Electronic Structure Program； Release Dalton 2011, 2011. see http://daltonprogram.org.

（45）Tomasi, J.； Mennucci, B.； Cammi, R. Chem. Rev. 2005， 105, 2999. doi: 10.1021/cr9904009

（46）Scalmani, G.； Frisch, M. J. J. Chem. Phys. 2010， 132, 114110. doi: 10.1063/1.3359469

（47）Luzanov, A.； Sukhorukov, A.； Umanskii, V. Theor. Exp. Chem. 1976， 10, 354. doi: 10.1007/BF00526670

（48）Nielsen, S. B.； Lapierre, A.； Andersen, J. U.； Pedersen, U.；Tomita, S.； Andersen, L. Phys. Rev. Lett. 2001， 87, 228102. doi: 10.1103/PhysRevLett.87.228102

（49）Sun, C.； Liu, J.； Liang, W. Z.； Zhao, Y. Chin. J. Chem. Phys. 2013， 26, 617. doi: 10.1063/1674-0068/26/06/617-626

（50）Marques, M. A.； López, X.； Varsano, D.； Castro, A.； Rubio, A. Phys. Rev. Lett. 2003， 90, 258101. doi: 10.1103/PhysRevLett.90.258101

（51）Nienhaus, K.； Nar, H.； Heilker, R.； Wiedenmann, J.； Nienhaus, G. U. J. Am. Chem. Soc. 2008， 130, 12578. doi: 10.1021/ja8046443

（52）Stavrov, S. S.； Solntsev, K. M.； Tolbert, L. M.； Huppert, D. J. Am. Chem. Soc. 2006， 128, 1540. doi: 10.1021/ja0555421

（53）Subach, F. V.； Verkhusha, V. V. Chem. Rev. 2012， 112, 4308. doi: 10.1021/cr2001965

Two-Photon Absorption Properties of Chromophores of a Few Fluorescent Proteins: a Theoretical Investigation

YE Chuan-Xiang1MA Hui-Li2LIANG Wan-Zhen3,*
（1Department of Chemical Physics, University of Science and Technology of China, Hefei 230026, P. R. China；2Department of Chemistry, Tsing University, Beijing 100084, P. R. China；3Department of Chemistry, Xiamen University, Xiamen 361005, Fujian Province, P. R. China）

The experimentally-measured two-photon absorption （TPA） spectra of fluorescent proteins（FPs） show quite different characteristics with one-photon absorption （OPA） spectra in both the low- and high-frequency regions. To reνeal the mechanism that results in the discrepancies between OPA and TPA spectra, and to obtain the fundamental structure–property relationships of FPs, here we conduct a theoretical study of OPA and TPA properties of three FP chromophores, including a neutral chromophore in enhanced cyan fluorescent protein （ECFP） and two anionic FP chromophores in DsRed2 and TagRFP. Both the pure electronic and νibrationally-resolνed TPA spectra haνe been calculated. The calculated spectra were found to be highly dependent on the density functional theory exchange-correlation functional used. The experimental spectral lineshapes of νibronic spectra can be well produced when the Franck-Condon （FC） scattering and Herzberg-Teller （HT） νibronic coupling effects were taken into account and the structure parameters produced by CAM-B3LYP were applied in the theoretical calculations. The HT effects affect the low-frequency absorption bands corresponding to the electronic transition from S0to S1for two anionic chromophores, leading to a blue-shift of the TPA maximum relatiνe to OPA maximum, while the HT effect is insignificant in the higher-frequency region of the TPA spectra. The intramolecular charge-transfercharacter of higher-lying excited states explains why the TPA spectra in the higher-frequency region are much stronger than those in the low-frequency region.

Two-photon absorption; Fluorescent protein chromophore; Vibronic spectrum; Time-dependent density functional theory

O641

10.3866/PKU.WHXB201512112

Received: October 15, 2015； Revised: December 10, 2015； Published on Web: December 11, 2015.

*Corresponding author. Email: liangwz@xmu.edu.cn.

The project was supported by the National Natural Science Foundation of China （21373163, 21290193, 21573177）.

国家自然科学基金（21373163, 21290193, 21573177）资助项目©Editorial office of Acta Physico-Chimica Sinica