燃烧反应动力学研究进展
2016-11-18甯红波李泽荣李象远
甯红波李泽荣李象远,*
(1四川大学化学工程学院,成都 610065;2四川大学化学学院,成都 610064)
燃烧反应动力学研究进展
甯红波1李泽荣2李象远1,*
(1四川大学化学工程学院,成都 610065;2四川大学化学学院,成都 610064)
化学反应动力学是燃烧过程分析的重要工具。燃烧微观反应过程、复杂反应机理、燃烧实验测量和湍流燃烧数值模拟等方面的研究工作已经取得了长足进步。本文主要介绍燃烧反应动力学研究方法,包括电子结构方法、燃烧反应热力学和速率常数的计算方法、燃烧详细机理构建和简化、反应力场分子模拟以及燃烧中间体测量、燃料点火延迟和光谱诊断等方面的研究现状。燃烧反应动力学具有很强的应用背景,燃烧过程化学物种的反应速率计算是湍流燃烧数值模拟的一个中心任务。由于燃烧反应网络的高度复杂性,我们对燃烧机理的认识还远不清楚。化学反应和湍流相互作用研究的深入、燃烧反应动力学和计算流体力学的协同发展,将对新燃料设计、燃烧数值模拟、发动机内流道流场结构的准确描述产生深远影响。
碳氢化合物;燃烧反应;压力相关;燃烧机理;燃烧诊断
1 引 言
人类从燃烧现象提出燃素说,开启了近代化学的大门,然而300多年后的今天,人类对燃烧本质的认识仍远落后于对燃烧的利用。燃烧反应动力学搭起了燃烧微观机制和宏观现象的桥梁,上世纪70年代末,国际上开始了燃烧复杂机理的研究工作,目前为止已经发表了单组分燃料和石油基混合燃料的一系列燃烧反应机理。但是,由于燃烧反应的高度复杂性,人们对复杂的燃烧反应认识仍然非常肤浅。
在燃烧反应基础研究方面,燃烧基元反应微观机制是认识燃烧本质和构建复杂燃烧机理的基础。由于燃烧过程一系列特有现象如热力学非平衡、高温诱发电子态激发等,使得成熟的过渡态理论、光跃迁模型等都不能准确描述燃烧,化学家们甚至不能给出燃烧中间体的态-态跃迁的清晰物理图像。燃烧反应是复杂的反应网络,存在多通道、非谐性和电子态热激发等特有现象。低温燃烧涉及大量过氧化物种的形成和消耗,这些物种的反应规律目前尚不清楚,因此构建燃烧机理来准确预测低温点火特性是一个难题和研究热点。燃烧中间体浓度的在线测量是跟踪火焰成分演变和验证燃烧模型的重要手段,由于光谱背景的复杂性,燃烧中间产物的实验测量和诊断仍然是一个热门的研究方向。
在燃烧应用方面,燃烧反应和燃气定向流动相结合,构成了运载工具的动力基础。基于燃烧反应机理实现化学物种生成速率计算和基于湍流模型实现控制方程求解的燃烧数值模拟方法,是发动机内流道流场结构全息化描述的最有效办法,因此,燃烧反应机理的构建是燃烧数值模拟的必备条件。然而,燃料分子结构的多样性和燃烧反应的复杂性,决定了反应机理研究的长期性。
化石燃料将在未来相当长时期内继续主导全球能源结构。人类利用能源的方式仍将以燃烧为主,这意味着将来的空天动力、舰船和车辆动力仍然依赖于燃料燃烧。燃烧反应动力学模拟从机理出发,结合计算流体力学,在一定的初始和边界条件下求解,得到物种浓度、温度、压力随时间的变化关系1,2。燃烧数值模拟在涡轮和冲压等空天发动机内流道流场结构描述方面具有特别重要的作用。依据不同研究需要,反应机理既可以是包含上万个基元反应的详细机理,也可以是较小的简化机理,或是基于某些目标构建的总包机理。燃烧反应动力学研究不仅是科学需要,更是国民经济发展的迫切需求。
燃烧反应的参数精确计算和微观反应机制的深刻认识,有助于燃烧的高效利用。燃烧反应复杂机理包含三个方面:(1) 裂解和燃烧所涉及的基元反应;(2) 每一个基元反应所涉及的动力学参数及其与温度和压力的依赖关系;(3) 动力学机理中涉及的每一种物种的热力学参数和输运参数。燃料燃烧过程中伴随着大量中间体的形成,通过实验手段测定这些物种的热动力学数据非常困难,因此需要量子化学方法来计算相关反应参数和输运参数。目前,碳氢燃料低温氧化反应网络研究取得了一定进展,但许多反应通道还需进一步的探索,如氢过氧烷基自由基QOOH + O2以及其后续的相关反应。另外,目前大分子碳氢燃料的燃烧反应机理是模拟发动机燃烧需要解决的重要问题之一,而主流的反应机理模型中大量的反应动力学数据都仅仅考虑了高压极限下的速率常数,对于燃烧中很多压力相关的反应类型如单分子的裂解、化学活化反应、异构化反应等均没有考虑压力对于化学反应速率常数的影响。尽管燃烧的反应复杂机理的提出已经有几十年,但燃烧反应参数的确定仍将继续是实验化学和理论化学的挑战性课题。燃烧条件可涉及到达几千度的温度和很高的压力,在实验室进行这些条件下的直接测量存在困难,通常需要对温和条件下的实验结果进行理论外推3。
构建实际燃料的详细反应动力学机理是一项长期任务,详细机理的构建可以是基元步骤列表的人工汇编,早先对小分子燃料如H2的燃烧详细机理常采用这种办法,也可以是基于计算机自动生成软件产生。近年来对汽油,柴油,航空煤油等实际燃料的燃烧详细机理构建常采用自动生成方法。这些实际燃料由多种化合物组成,随着燃料分子量的增大,物种数和基元反应数呈指数增加。此外,我们应用的大多数燃料是石油基混合燃料,复杂反应机理不可能包含所有燃料成分,因此常采用含有几种物种的替代燃料代表实际燃料4,其详细机理可涉及上千个物种和上万个反应。燃料燃烧涉及的大量中间体是活泼的自由基,其热力学参数和输运参数及基元反应的动力学参数用实验测量非常困难,需要依赖于理论计算。近年来量子化学和计算机的发展,促进了燃料详细反应网络研究和反应参数精确计算。但由于燃烧详细机理的复杂性和中间种数的多样性,反应参数的近似估计仍然是反应参数计算的重要手段。
燃烧反应详细机理的自动生成,通常是根据大分子体系碳氢化合物的燃烧机理的特点,机理生成软件通常按反应类产生基元反应。燃烧反应类型,特别是碳氢化合物的低温燃烧反应类型的搜寻是机理构建面临的挑战。对每一反应类中每一反应提供精确的温度和压力相关的速率常数、或是如何根据反应规则,快速给出近似速率常数,是机理构建的主要任务。
实验验证是发展燃烧反应机理的必要手段,需要将数值模拟结果与实验数据相比较来验证机理的合理性。燃料裂解和燃烧等相关动力学实验,能获得物种浓度、反应速率,宏观的燃烧参
数(如点火延迟和火焰传播速度)等实验数据,为动力学模型的验证和优化提供实验手段。当前的发展趋势体现在更加全面而准确的物种浓度和重要基元反应速率常数的高精度计算和先进的实验手段3,5,6。
燃烧过程一般涉及到化学反应和流动的耦合,需要燃烧涉及物种的输运参数,如扩散系数、粘度和热导系数。目前,这些参数的计算方法一般只是适用于稳定分子,从实验得到的参数也大多是针对稳定分子,而自由基参数还缺乏精确计算方法,大量自由基参数缺乏实验报导7。
由于燃烧反应的复杂性、燃烧测量手段的多样性和燃烧反应动力学在国防和国民经济的工程应用背景,燃烧研究成为一个重要的多学科交叉领域。本文重点介绍燃烧反应热、动力学参数、输运参数的计算、燃烧反应机理构建和模拟、燃烧测量和光谱诊断等方面的研究进展和存在的问题。
2 燃烧基元反应参数计算方法
燃烧反应机理热力学参数包含的物种的焓、热容及熵。其中,物种的焓一般采用绝对焓定义,即

式中,ΔHf为物质在298.15 K的标准生成焓。温度对H、热容Cp和熵S的影响常采用以下7参数(a1–a7)形式:
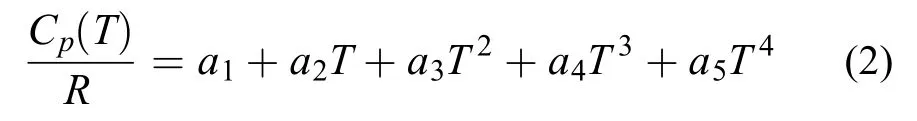
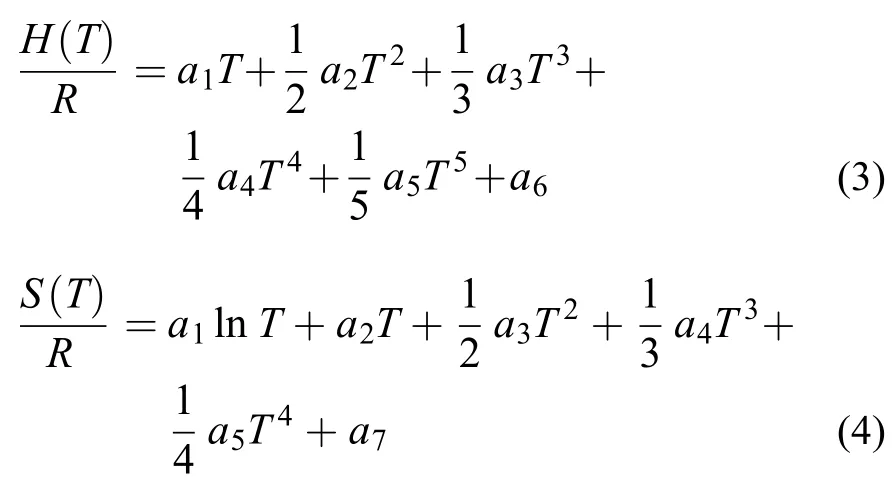
其中R为普适气体常数。为了适用于较宽温度范围的燃烧模拟,热力学参数一般拟合为低温段和高温段表达式。
燃烧反应机理中基元反应的动力学参数,是由不同温度下反应的速率常数k(T),按Arrenhenius方程拟合:
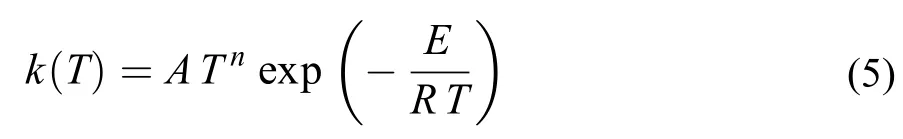
得到k(T)的3参数(A,n,E)形式。这种3参数拟合方式是便于数值模拟的一种数学处理,一些时候“活化能”等参数在拟合结果中的物理意义已经丧失。
在燃烧机理中,热力学和动力学参数可以是近似估算,也可以是精确结果。对核心机理中物种热力学参数和基元反应通常采用精确的实验数据或理论计算,而对机理自动生成程序中按反应类型给出的基元反应,速率常数目前多是按反应规则给出近似估计值。
2.1 燃烧反应热力学参数计算方法
在燃烧机理自动生成中,热力学参数通常取自现有的热力学数据库或文献报道,特别是核心机理中物种热力学参数。目前最常用的3个数据库是:(1) Ruscic等的ATcT数据库8,包含超过1300个有机物、自由基以及一些与燃烧和空气污染相关的无机物;(2) CRC化学与物理手册,该手册2010年版9提供了准确、可靠和较新的化学物理数据资源;(3) NIST数据库,NIST热力学数据库共收集了实验或各种计算水平得到的一系列有机物和无机小分子的热力学数据,也包含部分碳氢化合物的燃烧产物和中间体的热力学数据。此外,Green等10用外推到无穷基(CBS)在QCISD水平,考虑内转子非谐校正,结合键加和修正(BAC)方法,计算得到了碳氢化合物燃烧涉及的219个小分子或自由基体系精确的热力学参数。他们还指出了现有的热力学数据库存在的参数误差等问题;Curran等11汇编了碳氢化合物燃烧涉及的C1–C4小分子或自由基体系热力学参数,并对这些参数的不确定性进行了分析并给出推荐值。
在燃烧机理的自动生成中,很多物种热力学参数缺乏文献值,需要估算12。这些参数在燃烧模拟中除用于反应焓变的计算外,通常还用于逆反应平衡常数的计算,即通过正反应速率常数和热力学参数计算得到逆反应速率常数。因此,热力学参数需要保证逆反应速率常数与正反应速率常数的精度相一致5。热力学参数估算最常用的方法是Benson13提出的基团加和方法(GA):化合物分子可划分为基团结构单元,基团类型是根据中心原子类型及其连接原子类型和数目定义。化合物的热力学性质由这些基团热力学性质数值的加和代替,且同类基团采用相同数值。为了提高基团加和法的预测精度,可引入一些修正项,如顺反式、环张力、对称性等。对自由基体系,有两种处理方案:一种和非自由基体系一样;另一种方案为Lay等14提出的氢键解离增量(HBDI)方法,自由基体系的热力学性质可由基团加和法得到的自由基的母体分子热力学性质及母体分子失氢贡献加和得到。目前估算热力学参数的两个软件THERM15和THERGAS16,采用的方法分别为第一和第二种。基团加和法计算热力学参数的优点是快速、易于程序化和数据更新。采用基团加和法,一般情况下计算的热化学数据精度可达5 kJ·mol–1,但对有杂环的分子体系有较大误差,有时还缺乏一些基团贡献值7,使其应用受到限制。
在燃烧机理的自动生成中,除核心机理基元反应外,对按反应类型生成的基元反应,其反应速率通常是按反应规则近似给出。这种反应规则可以是整个反应类中所有可能基元反应都采用同一参数,也可以对反应类中反应进一步划分为子类,每一子类采用同一参数17,18,如过氧烷基分子内氢迁移反应。Sharma等19按氢迁移距离及迁移氢所在碳原子类型,把烷基过氧自由基分子内氢迁移反应进一步划分为许多类型,在CBS-QB3水平上计算得到从1–3氢迁移到1–8氢迁移各反应类速率系数规则;Miyoshi20按氢迁移距离及迁移氢所在碳原子类型和过氧基所在碳原子类型,把该反应类进一步划分为许多子类型,在CBS-QB3水平计算得到了从1–4氢迁移到1–8氢迁移各反应类及逆反应各反应类速率系数规则;在机理自动生成程序中,还可以按反应焓与动力学参数的关联关系,给出反应类中所有可能基元反应速率常数估计值,如Evans和Polanyi21提出的反应能垒和反应焓间的线性关系:


其中nH为可夺氢原子数;A,n和E0为某一特定自由基从烷烃中夺氢复分解反应的动力学参数,Δ0H为相同自由基从甲烷中夺氢反应的反应焓,ΔrH为该反应的反应焓,f为相关因子。
小分子体系势能面的精确计算近年来有较大进展,Harding等23,Pilling3,Truhlar等24对势能面计算方法及研究进行了综述。最近Pilling等25还对大气化学动力学研究方法进行评述,对动力学计算涉及到的电子结构计算方法进行了详细介绍。
用于计算电子能量或势能面的电子结构方法可以划分为单一方法和多种水平的组合方法。电子能量计算通常可以分为三类25:(a)从头算方法,(b)密度泛函理论(DFT),(c)组合方法。
从头算方法的出发点为Hartree-Fock (HF)方法,根据自旋相反电子占据空间分子轨道的异同,又常分为闭壳层HF(RHF),自旋非限制开壳层HF(UHF)和自旋限制开壳层HF(ROHF)。HF方法忽略了电子相关,其计算能量有较大误差,通常不能用于化学反应能或反应焓变化的计算。对电子相关能的处理方法为post-HF方法,最基本的是基于变分原理的组态相互作用(CI)方法。CI方法将波函数表达为一系列组态函数展开,其展开系数由变分法优化得到。包括所有电子到所有轨道的可能激发组态的CI称为全CI (Full-CI)。非全CI的单纯CI方法,如CISD,因不满足大小一致性,现在很少用于化学反应动力学计算。而对CISD方法经过大小一致性修正的QCISD方法26,近年来普遍用于反应动力学计算,可以得到与CCSD方法接近的结果27。包含三激发微扰修正的QCISD(T)方法可以得到与CCSD(T)方法接近的结果28。另一种post-HF方法是近年来普遍采用的耦合簇方法(CC)。包含一个电子激发算符和两个电子激发算符的簇算符的耦合簇方法,称为CCSD方法。簇算符包含的激发电子算符越多,耦合簇方法的计算精度越高。耦合簇方法已成为计算化学中电子能量计算最广泛采用的精确方法,但其计算量随分子大小N的增加而急剧增加。对大部分燃料分子体系的计算难以实现。在CCSD方法基础上对三激发贡献进行微扰修正的称为CCSD(T)方法,其计算量与N7成正比。一般认为从头算方法的计算精度有以下顺序25:HF < MP2 < MP4 < QCISD(T) ≤ CCSD(T) < Full-CI。CCSD(T)方法常用为精确计算的基准方法。以上方法,都是单参考方法。在某些情形下,裂解和燃烧涉及到断键反应或涉及双自由基的反应,需要考虑多参考效应,如采用多参考CI (MRCI)方法或多参考微扰(MRPT)方法。最常见的多参微扰方法是考虑到二阶能量修正的CASPT2方法(或CAS-MP2方法),它是在CASSCF水平基础上加上二阶微扰修正。多参考微扰CAS-MP2或CASPT2方法及多参考组态相互作用(MRCI)方法是考虑多参考效应最常用的精确方法,但都只能用于燃料小分子体系的热力学和动力学参数的精确计算。
DFT在量子化学计算中得到了广泛的应用,一般认为其计算精度与MP2相当,但其计算成本更低。在燃烧反应动力学研究中,DFT是势能面计算的最常用方法。通常选用恰当的DFT泛函,对所研究体系可能反应途径进行探索,找到过渡态和中间体的几何结构,并用该方法进行几何结构优化和频率计算,然后用高精度的从头算方法如QCISD(T)或CCSD(T),或组合化学方法进行单点能精确计算。
组合方法又称模型化学方法,是基于多种水平从头算方法的经验组合。从头算方法计算分子体系的单点能,其精度依赖于从头算级别和基组大小。精确计算要需高级别从头算方法如CCSDT或者CCSD(T),推广到无穷基极限,因此计算局限于几个重原子的小分子体系。对较大体系,通常采用组合方法。组合方法是通过一系列级别和不同基组组合从头算外推,因基组大小,电子相关,旋轨耦合等对单点能的贡献,从而达到对高级别大基组或完全基组极限的单点能的估计。组合方法的基本假定是这些贡献具有加和性,电子能量的修正可以通过对这些贡献的修正相加得到。已有许多组合方法报道,早期最常用的是Pople的Gaussian-n方法,即G2,G3,G3X,G429–32和Peterson等人的CBS系列:如CBS-QB3和CBS-APNO33–37。这些方法平均精度可达到化学精度(4.18 kJ·mol–1),如G4理论32对G3/05测试集的平均绝对值偏差仅3.47 kJ·mol–1,远小于G3理论得到的平均绝对值偏差4.73 kJ·mol–1。近年建立的Weizmann-n系列38–41,HEAT42,43,焦点外推(Focal-Point Extrapolation)44,45等组合方法,计算的生成焓精度可达±2 kJ·mol–125。
2.2 热力学参数计算
燃烧模拟需要的热力学参数是物种的焓或者生成焓、熵、热容。燃烧反应存在大量的自由基,热力学参数难以依靠实验获得,因此理论计算成了获得燃烧反应热力学参数的主要途径。热力学参数计算采用理想气体模型。焓的计算涉及到电子能量贡献配分函数及平动、转动、振动配分函数的贡献,而熵和热容只涉及到平动、转动、振动配分函数贡献。在刚性转动-谐振子近似下,平动和转动配分函数只与分子组成和几何结构有关,振动配分函数只与振动频率有关,所以这些配分函数的计算只依赖于几何结构优化和频率分析,这通常采用同一从头算水平,而且经验表明,几何结构优化通常只需要较低级别从头算和较小基组,而频率只需在同从头算级别下对频率分析得到的所有频率乘以相同的标度因子,则可得到较精确结果。对不同从头算方法和基组计算的振动频率标度,人们做了大量的系统工作,如Truhlar46、Wilson47、Moran48等。熵和热容不涉及电子配分函数贡献,只需要较低计算水平便可得到好的结果。更精确的计算需考虑非谐效应的影响。焓或者生成焓的计算因涉及电子配分函数的贡献,其计算精度强烈依赖于电子能量的精度。由量子化学方法和统计热力学结合计算的理想气体模型下气相物种焓,通过原子化焓方法可以得到气相物种的标准生成焓。计算的物种的标准生成焓以碳氢燃料分子CxHy为例,基于标准生成热的定义,原子化焓方法计算标准生成热过程如下:
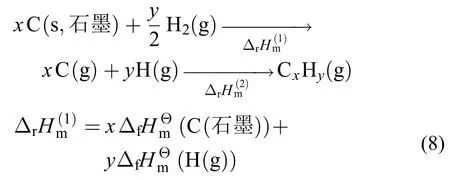

(8)式中,分别为石墨和气态氢原子的标准生成热,通常采用实验数据;(9)式为CxHy(g)的原子化过程的逆过程,其反应焓变由量子化学计算得到。因而原子化焓方法计算标准生成热的精度取决于计算焓的从头算方法的级别。
热力学计算的追求目标为通常意义上的化学精度4.18 kJ·mol–1。单一的电子结构方法中用于标准生成焓计算实际可行的标准方法是CCSD(T)外推到无穷基极限方法49。由于各种组合方法计算量大,仅能用于较小分子体系。在燃烧反应计算中,CBS-QB3方法是近年来人们最普遍采用的方法之一,但最近Simmie 等50,51分别用G3、G4、W1BD、CBS-APNO、CBS-QB3等组合方法对45个CxHyOz稳定分子和38个CxHyOz自由基的标准生成焓进行了计算比较,发现其计算精度顺序为G4 > G3 > W1BD > CBS-APNO > CBS-QB3,其中CBSQB3计算误差最大,某些情形下可能得到错误的结果。
对于大分子体系标准生成热的计算,人们提出了通过设计等键反应(isodesmic)或等电对反应(isoggric)间接计算标准生成焓的思想。等键反应是指反应前后同一类型化学键的数目守恒,而等电对反应是指反应前后电子对的数目守恒。等键反应因其反应前后同一类型键的数目守恒,其大部分相关能可以抵消,因此其反应焓对从头算级别依赖不大,从而可以在较低从头算级别得到较精确的反应焓变,进而利用这种思想在较低从头算级别计算得到较高精度的标准生成焓。等键反应计算标准生成焓的不足之一是,对同一目标化合物,通常可以设计不同的等键反应,其计算结果也会带来差异。因此,Pople提出了键分离反应(BSR或IBS)52,53,用BSR方法,可以设计出最简单的等键反应,且设计方法是唯一的。用BSR方法,可以进一步提高标准生成热的精度,可以在较低水平下得到较精确的结果。Ramabhadran等54,55依据BSR思想,基于连接信息,建立了大分子体系由小分子片段逐级构造(CBH)的方法,根据分子片段大小不同,划分不同层次的CBH模型。除了等键反应方法外,人们还建立了一系列近似从头算计算的热力学参数基础上进行统计修正的方法。一种统计修正的方法是键加和修正方法(BAC),在某一级别的从头算方法计算的生成焓基础进行修正,其修正为各键的贡献的加和,各种类型的键的贡献由测试集化合物提高最小二乘拟合统计得到56,57。BAC方法修正可使计算精度得以大幅提高。此外还有基于原子贡献的统计修正方法58,更复杂的统计修正方法,是对更复杂的分子结构特征进行线性或非线性修正。徐昕等59基于B3LYP的神经网络修正,建立了系列的X1、X1s、X1se方法,对一系列标准数据集的标准生成焓计算表明,其精度介于G2和G3之间。我们对B3LYP/6-31G(d,p)计算的771个闭壳层分子和自由基的标准生成焓进行了线性的统计修正,其平均绝对偏差从20.50降到了8.79 kJ·mol–160。
2.3 化学反应动力学计算
燃烧反应的动力学处理主要是结合电子结构理论和统计速率理论,计算温度相关和/或压力相关的基元反应速率常数。速率常数的计算精度不仅取决于描述势能面和单点能计算所采用的电子结构理论,还取决于所采用的统计速率理论。二者的结合可参阅Zádor等61的综述。化学反应动力学的计算方面,传统过渡态理论即正则过渡态理论,已成为动力学计算的最常用统计速率理论。通常,用DFT方法或MP2方法等中等级别从头算方法优化、并通过频率分析确认得到所研究反应的反应物和过渡态的结构频率,再在高级别从头算方法如CCSD(T)或组合方法,得到其精确的单点能或吉布斯自由能。根据过渡态理论,将速率常数表示为25

其中κ为隧穿系数;σ是反应的对称数,kB和h分别为Boltzmann常数和Planck常数,T是温度,Q≠和QR分别表示过渡态和反应物的配分函数(包含平动、转动、振动贡献),ΔV≠为经典势垒,是过渡态和反应物电子能量的差,ΔG≠为过渡态和反应物吉布斯自由能的差。
过渡态理论可以很好地应用于有明显活化能垒的反应。变分过渡态理论是对过渡态理论的改进,对没有鞍点的反应,如自由基复合反应,一般采用变分过渡态理论,即根据过渡态理论速率常数表达式,沿反应坐标s对每一温度T寻找速率常数的最小值。变分过渡态理论给出的反应速率常数值为

用变分过渡态理论,需要反应物沿反应坐标的几何结构、频率、单点能等信息。对有能垒或过渡态的反应,用变分过渡态理论计算速率常数改进不大。
过渡态理论和变分过渡态理论计算得到的速率常数都是高压极限的速率常数,然而燃烧基元反应中许多反应的速率常数除了与温度相关外,还与压力相关。这些反应类型有62自由基-自由基结合反应、自由基加成到多键的反应、消去反应、分解反应、异构化反应及双分子化学活化反应。Zhang和Truong63提出了反应类过渡态理论(RCTST)。这种方法将有相同反应中心的化学反应分为一类,通过同一反应类中两反应类比的方法,结合传统过渡态理论(TST),在低级别从头算水平得到了较精确动力学参数。这一理论已广泛用于反应类动力学参数的计算64–67。该理论的缺陷是只能在传统过渡态理论框架下实现计算,因而只能得到高压极限速率常数,并只适用于有能垒化学反应,目前尚未发现用于微正则速率常数的计算。我们对反应类中的反应进行了研究68–70,发现反应类中两反应的差以及由反应物到过渡态的过渡反应的差均近似为等键反应,进而将等键反应概念引入反应类过渡态理论,对大分子反应体系的动力学参数计算在较低从头算水平上得到较精确的结果。
2.3.1 速率常数的压力效应
以单分子反应AB = A + B为例,通常认为该反应为至少两步过程的结果:
第一步是AB分子通过碰撞而活化或去活化过程,第二步是化学反应过程。这两步过程是竞争的过程,第一步能量转移速率与反应物分子和第三体的碰撞频率有关,从而与第三体浓度,进而与体系的压力有关,因此该反应的表观速率常数k(T)与压力相关。压力相关速率常数的计算涉及微正则速率常数k(E)和能量转移模式。对压力相关速率常数的近似计算,通常采用QRRK(quantum Rice-Ramsperger-Kassel)方法计算微正则速率常数k(E),而能量转移可用修改的强碰撞假设。精确的压力相关速率常数的计算,需要在高精度电子结构计算的基础上结合RRKM(Rice-Ramsperger-Kassel-Marcus)理论与主方程近似。对有能垒的单分子反应,微正则过渡态理论-RRKM理论的微正则速率常数表达式为,

其中ρ(E)为反应物在能量为E的态密度,N≠(E)为过渡态能量 ≤ E的状态和,h为Plank常数。对无能垒反应,则通常用微正则变分过渡态理论:
其中s为反应坐标,N≠(E, s)反应体系在反应坐标s处能量 ≤ E的状态和。
RRKM理论给出了单分子反应AB = A + B反应物分子在能量E的微观速率系数k(E),该反应的表观速率系数k(T)为其平均:

其中χ(E, t)为反应物分子在时间t能量为E的分布,是反应物分子与第三体M碰撞引起的能量转移和化学反应竞争结果,可由一维主方程描述:
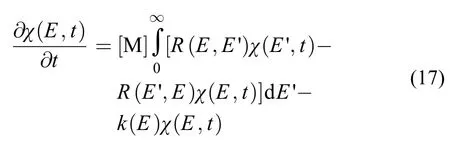
其中R(E, E')为从能级E'碰撞能量转移到能级E的速率系数,R(E', E)则为从能级E碰撞能量转移到能级E'的速率系数。方程(17)为单分子通道反应主方程的连续形式。为了数值求解,需要把该方程表达为系数形式:把连续能量E表达为离散能量Ei,其能级间隔为相同的δE,则积分形式的主方程变为求和形式的主方程:

方程(18)常写为矩阵形式:

其中χ为列向量,矩阵J定义如下:

主方程的求解方法有很多,其中Gilbert和Smith71的本征值方法是最普遍采用的方法。可以证明,其表观速率系数为

其中λ0为矩阵J的最大本征值。
对应于RRKM理论的含角动量量子数J的微正则速率常数k(E, J),需要采用描述反应物分子在能量为E和角动量为J的分布的二维主方程。二维主方程表达形式与一维主方程表达形式相似。但是,目前在燃烧模拟中关于压力相关速率常数的计算,主要还是以一维的主方程为主。一方面,Miller等72,73的相关研究中表明,很多情形下一维和二维的结果基本是一样的;另一方面,一维主方程比二维主方程要大大简化。
碰撞能量转移速率系数可以用能量转移概率P(E, E')及碰撞频率ω(E')表示:

以硬球模型(HS)计算的碰撞频率为
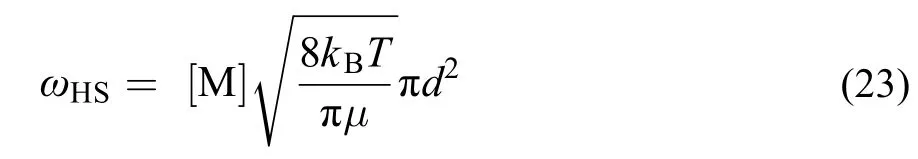
其中d为硬球直径,μ为约化质量,kB为玻尔兹曼常数。而实际气体分子间碰撞是以Lennard-Jones作为分子间势能模型:

其中ε为势阱深度,δ为势能为零点时粒子间距离,则实际气体碰撞频率为
其中Ω称为碰撞积分,其计算有不同的表达形式如Roos74:,或Troe75:因此,碰撞频率的计算需要准确的Lennard-Jones(L-J)参数(ε,δ)。而到目前为止,对碳氢化合物的许多燃烧中间体自由基都缺乏L-J参数报道。物种的L-J参数可以通过与物质性质,如粘度、或临界参数(Tc、Vc、Pc)的相关物性或基团贡献法近似计算,但这些方法均局限于稳定分子,还缺乏可用于自由基的通用方法,因而在动力学参数计算中目前大多采用相似大小或相似组成分子的参数近似代替76。最近,Jasper和Miller77提出了从高精度从头算(如QCISD/CBS水平)计算得到的多维势能面出发,通过取样平均并优化得到LJ参数的方法,并得到了一些较小自由基的L-J参数。该方法的缺陷是计算量大,如对烷烃分子,每一固定分子间距离需要计算10000个单点能,因而计算极为费时,且高精度量子化学计算也把该方法局限到了较小分子体系。Cambi等78建立了LJ参数与极化率的相关关系,从而可以由极化率估算L-J参数。该方法可用于自由基L-J参数的计算,但Cambi等人的工作只局限于小分子体系,应用于大分子体系L-J参数的计算,还有待进一步验证。
在主方程方法中,除了涉及到碰撞频率的计算,还涉及到能量转移概率P(E, E')计算。碰撞能量转移概率的数值模型有很多79。但普遍采用的都是所谓的指数下降模型,即从高能态E经碰撞到低能态E'的能量转移概率P(E', E)为

其中A为归一化系数,α为系数,与去活化过程中平均转移能量< Edown>成反比:α = 1/
压力对不同反应的速率系数的影响是不一样的,因而速率系数对压力相关的数学表达式也可能不一样。不同的表达形式适用于不同反应类型或有不同的局限。对单分子离解反应(如C2H6= CH3+ CH3)和自由基复合反应 (如CH3+ CH3= C2H6),属于单通道单势阱反应,其表观速率常数在高压下趋于极限,在低压下与压力成正比,在中间压力区域存在压变现象,即所谓的Falloff区,反应表观速率常数随压力增加而增加,用Troe表达式能较好地反映此规律:

其中k0和k∞分别是低压极限和高压极限的速率常数,k是压力相关的速率常数。

Pr是折算压力,[M]是三体的浓度。
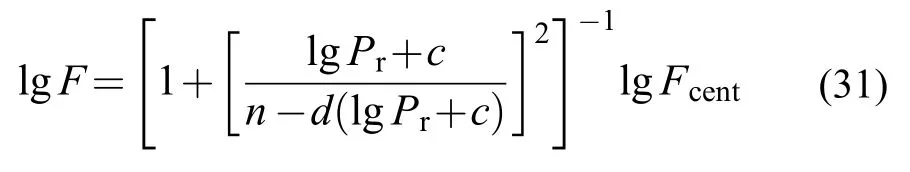
式中常数c,n,d,Fcent分别为
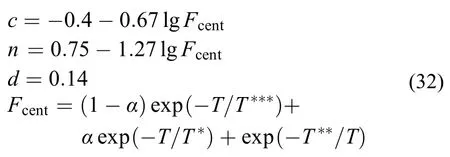
其中的α,T***,T*,T**需要指定。
对化学活化反应如CH3+ CH3= C2H5+ H反应,首先是两自由基CH3复合形成高能量的C2H6*,该高能激发态是通过化学键的生成,即所谓化学活化得到的。生成的高能激发态的C2H6*,可以与第三体分子(M)碰撞得到稳定化的C2H6,同时可竞争性地分解得到新的产物,如C2H5+ H。压力越大,对稳定化C2H6的形成越有利,所以对CH3+ CH3= C2H5+ H反应,压力越大,反应表观速率常数越小。该类反应在高压下不趋于极限,反而是在低压下趋于极限。用SRI(Stanford Research Institute)表达式能较好地反应此规律:

对多势阱多通道反应,其表观速率常数与压力的相关关系比较复杂,不能用Troe或SRI公式作为近似,常用切比雪夫多项式和指数内插表达形式。对切比雪夫多项式形式:
其中,

由于切比雪夫多项式的变量必须归一化到[–1, 1]区间,因此必须设定压力最小值Pmin和最大值Pmax,用于压力变量的归一化,压力超出此范围则切比雪夫多项式无定义,因而用比雪夫多项式形式表达的压力相关动力学参数只适用于Pmin到Pmax压力范围内的燃烧模拟。对指数内插表达形式,这种方法不给出压力相关的动力学参数解析表达形式,而是给出不同压力离散点的动力学参数,对压力不在这些离散点的动力学参数由指数内插得到,对超出离散点范围的压力的动力学参数,则用邻近的压力最小值或压力最大值的动力学参数近似代替。
目前,燃烧机理中许多动力学参数只考虑到温度依赖关系,而没有考虑到压力依赖关系。由于对大量压力相关的反应类型缺乏速率常数压力相关规则的研究,除RMG(reaction mechanism generator)81外,大多机理自动生成程序对按反应类型生成的基元反应,都没有考虑压力相关。
2.3.2 非谐效应
分子振动频率可以在不同理论级别计算82。计算量最小的近似是谐振子近似,是基于某一级别的电子结构理论计算的能量的二阶导数得到。该近似得到的是非耦合的谐振动频率。为了改善所计算频率的精度,可以用从通过谐频率对实验数据拟合得到的标度因子标度。人们已建立了对一系列不同基组不同理论级别的标度因子,但这种方法有较大缺陷,对包括从刚性伸缩模式到大幅度扭曲的振动模式的所有振动采用同一标度因子是不恰当的,因为并非所有模式的谐性或非谐性都是一样的,Johnson等83提出了对高频振动和低频振动分别采用不同标度因子校正。对振动光谱细节的精确预测需要更严格的方法,可以在高级别从头算得到的精确势能面基础上,通过求解核运动方程,得到振动光谱的精确预测,其核运动方程求解方法主要包括振动自洽场(VSCF)或振动组态相互作用理论方法84和振动微扰理论方法85。但这些方法大都只能用于非常小的分子体系。所以人们对大分子体系通常是在谐振子近似的基础上对非谐效应进行修正,一般也不考虑振动模式的耦合。
不同振动模式其非谐性地大小是不一样的。对应于键伸缩或键角弯曲的高频振动,在低温条件下可以用谐振子势较好描述,因此非谐性较小。但在高温条件下,分子可以处于高振动激发态,分子体系大幅度偏离低温平衡构型,非谐效应非常显著,通常用Morse势或高阶(如4阶)多项式表示。对应于分子单键内转动的低频振动,即使在较低温度下其非谐效应也较显著,而且其势函数用周期的傅里叶级数才能更好地描述,因此通常将低频振动转化为分子内转子处理。
对于内转子的处理,要解决的主要问题是转子的约化转动惯量的确定和内转动Schrödinger方程的求解5。通常,需要通过频率分析识别出对应于单键转动的低频振动,用从头算方法进行势能扫描并按傅里叶函数或余弦函数形式拟合得到转动Schrödinger方程的势能函数。如果转动势垒高度远大于kT,则可以按谐振动处理;如果势垒远小于kT,则该振动按分子内自由转子处理;如果势垒介于二者之间,则按分子内受阻转子处理。对分子内受阻转子的研究方法,文献中有大量报导,其详细讨论不在本文范围。其中最常用的方法有Pitzer和Gwinn86提出的非耦合一维受阻转子的列表法。Van Speybroeck等87研究了内转动耦合对配分函数的影响。
非谐效应对热力学参数的影响是通过对振动配分函数的修正得到的。在高温下,非谐效应对低频振动和高频振动的配分函数都有显著影响,因而对热力学参数有显著影响,特别是对熵和热容的影响较大。Vansteenkiste等88研究了内转子修正对从乙烷到正辛烷的一系列烷烃的熵和热容计算的影响,发现随着体系的增大,熵和热容的非谐性越大。对碳烷烃,在谐振子近似下,其熵和热容有近10%的标准偏差,而经受阻内转动修正后,其标准偏差可降到低于1%。因此谐振子近似下高温热力学参数有较大误差,非谐效应修正对用于高温燃烧模拟的热力学参数的精确计算非常重要。
非谐效应对动力学参数的影响,对正则过渡态理论是通过修正过渡态和反应物配分函数,同时还通过修正隧穿效应,实现速率常数计算的修正。而对微正则过渡态理论是通过修正过渡态状态数和反应物态密度以实现速率系数计算的修正。研究发现89,不同振动模式非谐性对动力学参数计算的影响是不一样的。在采用正则过渡态理论计算速率系数时,作为不介入反应的“旁观者”振动模式,非谐性对过渡态配分函数和反应物配分函数的贡献可以抵消,而其它介入反应的模式,如在键离解过程中的碎片间键弯曲模式,其非谐性对过渡态配分函数和反应物配分函数的贡献方向是相反的,所以,在某些情形谐振子近似下的过渡态理论可以得到较好结果,或者在此情形下只需对对应于分子内转动的低频振动采用受阻转子近似处理。特别地,林圣贤、姚丽等90–93建立了基于Morse势的非谐RRKM理论,对大量反应体系反应速率系数受非谐性的影响进行了系统研究,所有振动模式都按非谐Morse谐振子处理。
2.3.3 隧穿效应
反应速率计算采用的传统过渡态理论是经典理论,将原子核当做纯粹的经典粒子来处理并没有考虑到量子效应。化学反应中,对于有能垒的反应特别是氢迁移反应隧穿效应不能忽略。文献中对于隧穿效应校正有许多的方法,其中最简单的是Wigner等94提出的抛物线函数形式的隧穿效应校正。其温度依赖的隧穿效应系数κ(T)为

其中ν≠是过渡态的虚频。这种方法通常不能准确描述隧穿效应,对于实际势能面的拟合不能仅仅依赖于虚频。Eckart函数包含了对一维势能曲线的非对称性校正,因此能够提供真实的势能函数,而且Eckart势可以拟合再现鞍点的曲率和反应的放热性95。由于其计算量不大而且在研究的温度范围内能保证足够的精度,因此这个方法被广泛的应用于理论燃烧动力学研究。Truhlar等96,97提出了更加复杂的计算隧穿效应的方法,发展了一套半经验的方法用来计算多维的隧穿效应系数。由于这些方法需要沿着反应路径的详细信息,因此计算量大。对于曲率较小的反应,一般采用小曲率隧穿效应(SCT)方法。大曲率隧穿效应(LCT)方法通常对于多数反应体系都适用,但是需要更多的势能面的信息,相对较复杂。更多的细节可以参考文献98。
2.3.4 激发态自由基
碳氢化合物燃烧反应是高度复杂的反应网络,燃烧过程发光涉及一些自由基和激发态物种的参与。低温下的燃烧发光一般是由化学发光引起,即通过化学反应产生处于电子激发态的物质,常见的有OH*、CH*、CO2*、C2*等激发态自由基,这些激发态物种对火焰结构有较大影响。目前为止,只有少量的燃烧模型对这些物种(主要是OH*和CH*)的浓度历史进行了模拟99–101。自由基CH2是最重要的燃烧中间体之一,该自由基的基态是低活性的三重态3CH2自由基,而第一激发态是更具活性的单重态1CH2自由基102,103。单重态1CH2自由基与乙炔反应生成C3H3和H,该反应对芳环形成,继而对碳氢化合物燃烧碳烟机理起重要作用104。单重态1CH2自由基可通过碰撞系间窜越到三重态3CH,与其化学反应是竞争的过程。Blitz等105计算2表明,1CH2+ C2H2反应的速率系数随温度增加而急剧降低。由最近的研究106表明机理中激发态的OH*、O*、C2*相关的化学反应的加入,会减小机理预测的点火延迟时间,增大层流火焰速度。由于激发态反应通常伴随着碰撞能量转移引起的物理竞争过程,这些反应的速率常数的精确计算需结合主方程方法,而激发态速率常数的计算和涉及电子激发态碰撞能量转移模型的建立仍是计算化学面临的挑战,因此目前燃烧机理模型中还基本没有考虑涉及自由基激发态的反应步骤。
2.4 输运参数的计算
正如化学反应热、动力学参数对构建燃烧模型是必须的,分子的输运数据对燃料燃烧流动模拟也同样重要107。碳氢化合物燃烧火焰的剖面形状、火焰传播速度、污染物的产率的模拟结果跟输运数据密切相关108。Esposito等109采用不同的方法做局部灵敏度分析,发现在特定情况下,输运系数显著地影响到火焰的性质。基于广义非均质反应流的化学动力学模型的验证和优化必须包括对分子输运模型的分析110。Grcar等111的研究表明熄火拉伸率和层流火焰传播速度的预测对反应和输运性质同样敏感。此外,很多工作提出输运数据的不确定性和计算反应速率常数的不确定性对燃烧模拟结果具有同等重要的影响107,112。Brown等108广泛地分析了输运数据的预测方法,结果表明需要重新审视燃烧模型中输运数据的计算方法。他们的敏感度分析结果也表明在火焰模型中,准确的输运数据和精确的反应速率同样重要。此外,他们也认为精准的火焰模型需要同时具备准确的化学动力学参数、输运数据和热化学数据。
输运参数的估算方法有很多,可以参见Grcar111,Paul112,Middha113以及Brown114等的研究。最近Brown等108对于燃烧模拟中的输运参数的计算方法给出了详细介绍。对燃烧动力学模拟中输运参数的计算,最常用也是最简单的方法,是基于动力学理论的Chapman-Ensko方法115。在该方法中,需要用到分子间势能函数计算碰撞积分的值。目前,用的分子间势能函数表达式是L-J势(式(24)。
根据Chapman-Enskog方法,对气相燃烧模拟必需的输运参数:扩散系数D,粘度η和热传导系数λ的表达式别为7:

3 燃烧反应机理及应用
3.1 复杂反应机理构建
详细燃烧机理尺度随碳原子数的增加而呈指数增长,复杂碳氢化合物详细燃烧机理的构建需依赖于计算机自动生成。从上世纪80年代开始,对反应机理生成和软件开发进行了持续研究。目前最为流行的机理生成程序有Battin-Leclerc等116–118的Exgas程序,已经成功地运用到烷烃(C4–C16)、烯烃、环烷烃、醚类、醇类和酯类的机理构建,并在比较宽泛的条件下进行验证(温度范围550–2000 K)。四川大学开发的Reaxgen程序(http://ccg.scu.edu.cn)可以用于构建高碳烷烃和环烷烃的裂解和燃烧机理。其它机理自动生成程序有Clappier等119,120的CHMEATA程序,Vandewiele等121的Genesys程序,Broadbelt和Green等122,123的NETGEN程序,Green等122,124–126在XMG和NETGEN基础上的RMG程序,KUCRS程序127,Ranzi等128建立的MAMOX和DSMOKE程序129,Warnatz等130的Molec程序等。程序更详细的罗列参见de Vijver等7最新有关机理自动生成综述。
以RMG机理自动生成程序为例,RMG是目前为止唯一能考虑压力相关动力学反应网络的机理自动生成程序,其核心结构主要包括三部分。第一部分是生成器,主要包含处理引擎、物种池、分子数据库、反应类数据库等,其中处理引擎是中心模块负责处理各个模块的相互调用,物种池主要储存包括输入的物种、产生的物种和自由基,分子数据库主要存储预先定义的分子,反应类数据库主要包含机理形成过程中每一类反应的信息。第二部分是机理生成的终止标准和收敛,主要是以核心机理为基础,采用层级结构的办法逐级形成反应的详细机理,当生成的较小的物种在核心机理中出现时就不再生成此物种的相关反应。但目前对于碳氢燃料低温氧化反应机理的自动生成是一个比较大的挑战,低温氧化反应包含的反应种类特别多,以及产生的物种数量也比较庞大。第三部分是分子和化学反应的表示,包括物种的命名、成键的表示、正则算法和分子等价以及机器识别的SMILES语言表示,以及二维结构的检索等。
RMG能生成含有C、H、O、S等原子的分子和自由基的反应机理,目前还没有考虑离子和光化学反应等。其中采用活化物种算法 (ASA)来处理化学活化或者是热活化的物种,并直接与压力相关反应通道相连接。对于物种的热力学数据主要采用基团贡献法得到,其动力学数据库主要来源于Baulch131、Hansen132、Rasmussen133、Alzueta134等的文献,输运参数采用基团贡献法获得。另外,机理自动生成程序仅对已有确切速率规则的燃料体系具有较好的适用性,且多用于对模拟精度要求不高的情况,其所生成的C0–C4小分子核心机理、芳香烃机理以及直链烷烃、环烷烃低温燃烧机理等都还远不够成熟。
甲烷燃烧中间体包含氢气和一氧化碳,而高碳氢化合物燃烧的中间体包含低碳氢化合物,如甲烷、乙烷、丙烷、乙烯、乙炔等小分子体。碳氢化合物燃烧反应详细机理的构建通常是以分级结构方式构建,即从H2和CO的燃烧机理出发,逐步扩展到更高分子量碳氢化合物的燃烧机理。因此,不同碳氢化合物燃烧机理都涉及共同的小分子反应,人们在构造机理自动生成软件时,把包含小分子的反应(通常包含C4以下物种反应)作为共同的核心机理(core mechanism),而不同碳氢化合物燃烧涉及的更大分子的基元反应,则按反应类由计算机自动生成。核心机理又叫子机理(submechanism)或种子机理(seed mechanism),它包含了小分子反应(通常包含C4以下物种反应)的详细基元反应列表,同时给出了每一基元反应的较精确的动力学参数和涉及物种的热力学参数。核心机理通常是对氢气、一氧化碳、甲烷、乙烷、丙烷、乙烯、乙炔等小分子体系以层次方式构建,其热、动力学参数通常来源于实验或高精度量子化学计算,机理经广泛实验验证,如激波管实验、管流反应器、射流搅拌反应器和火焰研究。GRI3.0机理135作为最早的开源机理,最先被广泛用于燃烧模拟中。近年来多个课题组分别发展了各自的全面验证的核心机理,具体参见Supporting Information表S1。
机理自动生成程序是在核心机理的基础上,按反应类型给出基元反应列表,并给予恰当的动力学参数。对动力学参数,通常只给出近似数值,即根据反应规则对同一反应类型中所有反应赋予相同参数,或者按基团加和法对每一个基元反应给出近似的不同动力学参数,如Exgas自带的Kingas程序。而所有基元反应中涉及的物种的热力学参数也按基团加和法近似给出,如Exgas自带的Thergas程序。利用自动生成器可以更加高效和系统地构建详细燃烧机理,机理构建者可以在更高的水平上考虑具体的反应类型和具体的次级机理并应用到最终构建的燃烧机理中。自动生成程序本身具有的系统性和易操作避免了机理构建误差。目前,由于这些程序产生的详细机理的反应类型的不完备,动力学参数和热力学参数的近似性,所以目前机理自动生成程序还不能作为黑匣子使用,生成的机理需进一步优化。
机理自动生成程序的关键之一是反应类型的完整性。碳氢化合物燃烧在高温(T > 1000 K)和低温(T < 1000 K)的燃烧机理有较大差别,如图1所示。现在人们普遍认为,燃烧在高温和低温的区别中,烷基自由基与氧生成烷基过氧自由基(R· + O2= ROO·)的反应是最关键反应,该反应由于是强放热反应,其平衡常数强烈地依赖于温度,低温下有利于ROO·的生成,而高温下有利于反应R · + O2= R′ + HO2·,因而R · + O2反应生成ROO·及后续反应在高温下不考虑,而在低温下起关键作用61,136。因此,高温机理通常不包含烷基过氧自由基的后续反应,现在的大多机理自动生成程序中,高温机理包含的反应类型为9种。而在低温机理中,除了包含高温机理反应类型外,还包含烷基过氧自由基后续反应。现在的大多机理自动生成程序中这样的反应类型有16种137。详细的高温和低温反应类型举例描述见Supporting Information的List1和List2。

图1 R• + O2反应路径Fig.1 Reaction path diagram starting from R• + O2
低温燃烧的一个重要宏观特征是点火延迟的负温度系数效应。在一定自点火始温度和压力等条件下,经过时刻τign,体系中OH等自由基大量出现并且体系温度急速升高,这个时间τign称为点火延迟时间,图2所示采用激波管测量甲苯/O2/Ar的低压点火延迟时间138。点火延迟时间是衡量燃料燃烧反应难易程度的一个重要指标,在超声速燃烧等方面具有重要意义。一般认为,温度升高将提高燃烧反应速率,点火延迟时间随之缩短,但是,当点火温度在650–900 K范围内,可能出现温度上升反而点火延迟时间增长的现象,这种现象称为点火延迟的负温度系数(NTC)效应,其示意如图3所示。

图2 激波管测量的甲苯/氧/氩体系的低压点火延迟时间138Fig.2 Measurement of the ignition delay time of toluene/O2/Ar in shock tube at low pressure138

图3 点火延迟时间的负温度系数效应Fig.3 Negative temperature coefficient effect for ignition delay time
目前机理自动生成程序产生的高温机理(尤其是C0–C4小分子核心机理)已相对成熟,经过近几十年的理论和实验研究,能较好地用于高温燃烧模拟,而对低温燃烧模拟则常不尽人意。一方面,许多低温燃烧反应类型缺乏可靠的动力学参数,低温燃烧化学中涉及烷氧基和氢过氧烷基的反应对点火起着至关重要的作用,然而由于大分子反应的动力学数据利用量子化学方法计算困难,特别是对于过氧化物这类化合物的计算非常复杂。同时,由于这类物种反应的实验动力学参数匮乏,目前构建的大型碳氢燃料低温燃烧机理主要是利用反应类规则,将小分子动力学参数推广到大分子应用。另一方面,低温燃烧的反应路径有待进一步完善。目前对于链烷烃的反应类型有较好探索,但即便如此,最近仍有新的低温燃烧通道得到不断补充139–141。而对于烯烃、环烷烃、芳烃以及含氧化合物燃料燃烧所涉及的反应类型的研究还有待深入,特别是低温燃烧中涉及的醇类、醚类、酯类、酸类和醛酮类中间体。虽然目前构建的一些燃烧机理能够半定量地再现实验研究结果,如能很好地呈现负温度系数曲线的点火现象,但是在定量上仍存在较大误差,特别是在射流搅拌反应器和流动反应器中物种浓度实验数据模拟验证时误差比较大。Herbinet等142利用Exgas构建的正庚烷低温燃烧机理虽然在多数的模拟条件下能够与实验值吻合较好,但是部分物种浓度曲线包括醇、醛和酮类的物种浓度演变曲线仍然有较大的差异,因此需要对这些物种的反应进一步研究来改善低温燃烧机理的性能。
机理自动生成程序的另一个关键是热动力学参数的准确性。目前的机理自动生成程序,其热力学参数一般采用基团加和法给出近似数值,而动力学参数按反应类给出近似数值。所以,如何结合量子化学计算更新自动生成机理中热动力学参数、建立较为完善的热动力学参数数据库并与机理自动生成程序相结合是未来机理自动生成的发展方向之一。
机理自动生成程序的第三个问题是物种命名和物种判别。目前,不同研究小组开发的机理生成程序,其物种命名并不统一,这对机理通用性和不同机理生成程序产生的机理的比较带来困难。化学物种的命名,一直是化学计量学研究的问题143。目前,普遍流行的方法是在对分子中原子正则(canonicalization)编号基础上,用唯一字符串(如SMILES语言144或SMARTS语言145)表示。这样,通过直接比较字符串就可判别机理自动生成程序产生的物种是否为同一物种。一个包含n个原子的分子对原子有n!种编号,正则编号就是赋予分子与输入顺序无关的原子编号。但因为正则编号的算法有很多146–149,如Morgan算法150,Weininger算法151。不同机理生成程序可能采用不同算法,使得对同一物种产生的字符串不一样。人们建立了大量的基于分子二维拓扑结构比较分子异同的算法,所以,机理自动生成的发展方向,应是在机理生成的同时,给出每一物种的二维结构,以便于判断不同机理自动生成程序产生物种的异同。
根据常见的燃烧反应类型及规律,部分常见的单组分碳氢燃料(如正癸烷152,正庚烷153,正十二烷152,154等)以及混合燃料(如国产航空煤油RP-3)的替代燃料燃烧详细反应机理155得到了一定程度上的发展。能够较好地再现给定条件下的物种浓度分布(如图4所示)等。另外详细机理的组分和规模不断增大,也能够考虑中间体,污染物如NOx和碳烟,压力效应156,大分子燃料等157,但目前对于大分子燃料详细机理的构建还有许多科学难题。反应速率常数绝大部分来自于经验估测和低精度计算,缺少宽工况范围基础燃烧实验的支撑,导致反应机理对于燃料燃烧特性的描述准确度低。其次,常见替代燃料如环烷烃在开环裂解过程中会产生单重态和三重态的双自由基,这类双自由基反应参数的精确计算存在困难。此外,燃烧过程中包含大量的如3O + CO = CO2的自旋禁阻反应,涉及到非绝热过程的理论处理等。

3.2 燃烧反应机理的应用简介
在真实三维结构(如航空发动机燃烧室,图5)的湍流燃烧数值模拟中,要实现工程尺度的发动机内流道数值模拟,需要达到上亿个计算网格。

图5 发动机燃烧室结构(a)和温度分布数值模拟示意图(b)Fig.5 Combustor structure in aircraft engine (a) and temperature profile diagram for numerical simulation (b)
从连续性方程

可以看出,化学物种i的生成速率i通过需要燃烧反应机理进行解算。上式中,ρ为介质密度,Yi为物种i的质量分数,v为流体流速。燃料单分子或混合物的燃烧反应详细机理中,往往包含数以百计的化学物种,如果机理包含低温反应,这个数值更大。因此将燃烧详细反应机理与计算流体力学的控制方程耦合来开展三维燃烧数值模拟几乎无法实现。这样一来,机理简化成了将反应机理应用到实际燃烧模拟的必要步骤,而在目前的多数计算流体力学商业软件中,燃烧机理采用一些极为简化的燃烧模型所代替,如火焰面模型,涡耗散概念(EDC)模型等。这些计算模型远不能描述真实的化学过程,因此基于详细反应机理的机理简化,并通过简化机理实现流动计算中化学反应速率的解算,显然是燃烧数值模拟的发展方向。
目前主要的机理简化方法包括直接关系图法(DRG)158,基于误差传播的DRG方法(DRGEP)159,修正的DRG方法(revised-DRG)160,路径通量法(PFA)161,通量投影树法(FPT)162,钟北京等163提出的基于特征值分析的简化方法以及四川大学开发的机理自动简化程序ReaxRed(http://ccg.scu.edu. cn)等。
基于燃烧简化机理的湍流燃烧数值模拟根据对湍流的模型处理,目前常用的有直接数值模拟(DNS)164,大涡模拟(LES)165,概率密度函数(PDF)166等。在实际的燃烧过程中,化学反应迅速放热而引起密度变化,同时导致流体输运系数变化,从而影响介质的流动状态。另一方面,湍流引起化学组分浓度和温度脉动,从而强化组分的混合与传热,又反过来影响燃烧反应。因此,实际燃烧过程的湍流和化学反应的相互作用非常复杂,是一个科学研究的难点问题。
3.3 燃烧反应分子力场模拟
量子化学计算至今还不能得到可靠的、完整的反应体系的势能面。目前对于高维度的反应势能面计算仅限于包含3–6个原子的非常小反应体系,而燃烧体系中间体复杂且规模庞大,在量子化学势能面上构建反应机理实现数值模拟是一个严峻的挑战。量子化学方法需要针对每个反应进行计算,而对于实际的碳氢燃料的燃烧过程,涉及的反应数目极为庞大,依靠量子化学计算,难以获得燃料燃烧的完整化学反应网络。另一方面,随着分子力场的不断发展,分子模拟方法和算法已趋于成熟,分子模拟可以给出体系的动态信息,同时可以快速有效处理较大的模拟体系。
作为分子模拟方法向化学反应的延伸,反应力场方法近年受到越来越广泛重视。反应力场由多体原子间势函数作为基础,参数一般要拟合不同结构的能量及导数,力求能够正确描述原子组态相空间更广泛的区域。目前常用的反应力场主要有Brenner167开发的REBO力场及Goddard等168设计的ReaxFF力场。REBO力场中,键级参数被定义为多体相互作用势函数,并以此来确定原子所处化学环境并计算相应的原子对相互作用能量。REBO力场模型的主要特点是没有分子及原子类型的概念,只有元素类型的区别,所有势函数都基于原子,并且原子上没有电荷。另一种反应力场模型是由Goddard课题组的van Duin等168于2001年发展起来的首先用于碳氢化合物的ReaxFF 力场模型。与REBO力场相比,ReaxFF力场设计思路与经典力场有类似之处。在ReaxFF力场中,原子间的相互作用通过复杂的函数计算,区分为键长、键角、二面角、共轭、库仑、范德华及校正项等。除库仑相互作用以外,其他项都是由多体势函数构成。为了研究烃类燃料高温气相氧化的初始反应,van Duin等169扩展了ReaxFF反应力场的训练集,并将与这些反应相关的过渡态和体系的化学反应性包含进来,再通过与基于量子力学的训练集作对比优化力场参数,最终应用于碳氢化合物的氧化。用改进的ReaxFF力场研究了甲烷、丙烯、邻二甲苯和苯在极端条件下的氧化反应,以及JP-10裂解和燃烧的初始反应和动力学。作者将ReaxFF力场应用于研究大分子燃料如正十烷170,正十二烷171,甲苯172等的氧化和裂解。图6是采用ReaxFF力场模拟正十烷与燃料添加剂分子混合体的裂解反应始末状态170。

图6 ReaxFF模拟30个正十烷分子与10个添加剂分子,密度为0.12 g·cm-3的混合体系裂解反应构型演变:左图(0 ps)和右图(60 ps)170Fig.6 Images of initial (left, 0 ps) and final (right, 60 ps) system configurations of 30 n-decane with 10 fuel additive molecules at density of 0.12 g·cm-3using ReaxFF molecular simulation170
目前ReaxFF已经包括了元素周期表中一半以上元素的通用反应力场参数,并应用于燃烧、含能材料、催化等多个研究领域。基于反应力场的分子动力学模拟方法,可以动态获得燃料燃烧的微观化学动力学过程,对构建简化的反应机理可能有重要的指导作用。然而现阶段ReaxFF分子力场还仅限于高温下(如3000 K以上)的模拟,在这样的温度下,燃料的点火时间在ns级,分子模拟能够实现这样时间尺度的模拟。但是,在真实温度条件下(~1200 K),燃料的点火时间在ms级,分子模拟方法目前还无法实现如此大时间尺度的模拟。
4 燃烧测量和燃烧诊断
4.1 燃烧中间产物的浓度测量
燃烧是一个非常复杂的物理化学过程,既包含大量不同反应活性的异构体,也包含对燃烧化学非常重要但浓度很低的活性自由基。燃烧中间产物的测量主要是通过燃烧诊断技术来实现。传统的诊断技术主要分为两类:(1) 非干涉光学光谱技术,包括激光诱导荧光光谱、光腔衰荡光谱、相干反斯托克斯拉曼光谱等。激光诱导荧光(LIF)光谱是测量自由基的常用技术,当激光波长调谐到分子的某两个特定能级时,分子发生共振,吸收光子能量并激发到高能态,处于高能态的分子是不稳定的,它会通过辐射或非辐射方式释放出能量而返回到基态。分子通过自发发射返回基态所发射的光称为激光诱导荧光。在LIF的基础上,将线光源展成片光源来测量分子的受激发射,称为平面激光诱导荧光(PLIF)。PLIF光谱可以实时测量燃烧中间自由基如CH、OH、HCO等浓度和温度的二维空间分布信息173。(2) 萃取样品与气相色谱(GC)、质谱(MS)或者是GC/MS相结合的方法,其中燃烧中间体检测中最为有效的是分子束取样与质谱连用方法(MBMS),它能检测出稳定和不稳定的燃烧中间体。齐飞等174,175结合传统的MBMS方法发展了同步加速真空紫外光电离质谱方法(SUVU-PIMS),这种方法可以最小化不同中间体之间的相互干扰、区分异构体以及检测自由基,能够有效地避免其他电离技术的背景干扰,已经广泛的应用于燃烧中间体的检测和低压预混层流火焰结构的研究176–178。最近,Savee等179通过光致电离质谱结合同步生成可调真空紫外电离辐射方法首次从实验上证实了低温燃烧关键中间体氢过氧烷基自由基QOOH的存在,为理论上探究低温氧化反应机理尤其是氢过氧烷基QOOH的反应提供了关键性的证据。
4.2 点火延迟时间及高温基元反应速率常数
覆盖宽范围实验条件下的点火延迟时间是验证燃烧反应动力学模型合理性和正确性的重要实验数据。自点火研究需要均匀、等温和等压点火实验环境,目前测量点火延迟时间的装置主要有激波管和快速压缩机。这两类设备均具有瞬态均匀加热的特点,并能提供精确的温度和压力条件,非常适合用于点火延迟时间的测量。快速压缩机采用活塞进行等熵压缩加热,实验时间较长,约1–200 ms,适合测量低温高压下的点火延迟时间。激波管则采用平面入射和反射激波对介质进行绝热非等熵加热,采用缝合接触面、降低高压段气体声速等方法后,实验时间可提高到50 ms,亦能基本满足点火延迟时间的实验要求,激波管中入射激波和反射激波的传播如图7所示。激波管与快速压缩机结合可以覆盖宽温度、压力条件下的点火延迟时间测量。

图7 激波管x–t示意图Fig.7 Shock tube x-t diagram
近年来,Sung和Curran180利用快速压缩机开展了一系列碳氢燃料和生物燃料的实验和动力学模型研究,斯坦福大学的Hanson课题组181,182则利用激波管开展了大量碳氢燃料自点火的实验研究。为开展液态碳氢燃料点火延迟时间和点火现象的研究,人们对现有的化学激波管进行了改造,包括加热激波管和雾化激波管,雾化激波管测量的是雾化燃料点火延迟时间,包含了雾化过程所需的时间。加热激波管测得的是气相蒸发燃料的点火延迟时间,不需考虑相变过程,点火延迟时间直接反映燃烧动力学行为,因此加热激波管是研究高碳数碳氢燃料和真实燃油动力学的主要手段。人们习惯于将高温下的点火延迟时间ign与温度、压力、燃料及氧化剂浓度的关系拟合成如下关系式:

上式中Cfuel是燃料的浓度, CO2是氧气的浓度,CM是三体的浓度,E可理解为表观活化能。从上式可见,1/τign与温度T呈Arrhenius关系。Davidson等182采用激波管加热方式研究了Jet-A等燃料的自点火行为,张昌华等183,184在加热激波管平台上研究了碳氢燃料如三甲苯、RP-3等的自点火特性,并首次获得了国产RP-3航空煤油点火延迟的负温度系数效应(图8)184,这主要是由于高温和低温下燃烧反应机理的不同而引起的。

图8 低温下RP-3煤油点火延迟时间负温度系数效应184Fig.8 Negative temperature coefficient effect of RP-3 ignition delay times at low temperatures184
激波管不仅可以用来测量宏观的点火延迟时间,还是定量测量高温条件下微观基元反应速率常数的常用装置。基于Beer-Lambert定律,利用窄线宽连续激光和各种灯源,定量测定不同反应温度、压力等条件下的反应物或产物的浓度历程,从而获得基元反应速率常数。测量物种覆盖真空紫外区的H、O等原子共振吸收光谱,紫外-可见区的CH3、OH、CH、CN等的电子吸收光谱,红外区的H2O、CO、CO2、C2H4等的振动吸收光谱。Hanson课题组181致力于利用红外可调谐半导体激光吸收光谱(TDLAS)技术应用到激波管中研究基元反应速率常数,在高温基元反应速率常数测量方面做出了重要贡献。TDLAS技术是将波长调制到特定组分吸收频域,通过测量激光经过测量区的衰减程度,获得气态流场参数如浓度、温度、速度的一种燃烧诊断技术。Hanson课题组采用的TDLAS技术包括直接吸收光谱和波长调制光谱测量,波长从近红外到远红外,测量了燃烧过程中重要基元反应如O + H2= OH + H,H + O2= OH + O,OH + OH = H2O + O,H2O2+ M → OH + OH + M,H + HCO = H2+ CO,CH2O + OH = HCO + H2O等的速率常数。
燃烧基元反应动力学的实验研究方法还有激光闪光光解(LFP)。激光闪光光解对于自由基的浓度的测量具有较高的敏感性但一般温度局限在1000 K以下,如测量体系Cl + C2H6中形成C2H5的自由基185,以及测量低温条件下体系C6H11+ O2形成的OH和HO2自由基等186。
燃烧过程中间体浓度随时间的演变是化学反应动力学实验测量的重点问题。由于大量物种的存在和复杂的化学反应网络,实际燃烧过程的基元步骤测量存在较大难度。但是,可以采用光谱方法检测一些自由基的光谱强度随时间的演变历史。这种动力学测量对描述燃烧过程十分重要,特别是超声速流动条件下的燃烧过程,有限的燃烧室长度能否保证燃料的完全燃烧,直接影响到发动机推力。因此,对燃烧过程中间体的动力学观测有非常高的应用价值。图9是采用反射激波点火和ICCD瞬态光谱技术获得的正癸烷燃烧中OH、CH、C2等自由基发射光谱随时间的演变历史187,图中时间t = 0 μs对应于点火时间。从几个典型的光谱峰高随时间的演变可见,CH峰和C2峰在点火初期迅速升高,这时,正癸烷裂解是主要过程,但这两个发射谱峰在5 µs时达到最大值后迅速衰减,C2峰在15 µs前基本衰减完毕,而CH峰稍迟。OH的谱峰出现较晚,且在30 µs时尚未衰减完成,意味着燃烧中后期以燃料的氧化为主。这种光谱测量能直观描述燃烧过程的自由基演变过程,但基于光谱测量的动力学研究还有大量问题有待解决,包括更大自由基的光谱表征、光谱峰高与物种浓度的关联、光谱的精细结构以及光谱演变过程的动力学理论处理等。

图9 正癸烷/O2/Ar燃烧中三种自由基中间体的发射光谱强度187Fig.9 Time histories of emisson intensities from three intermidate radicals in the combustion reaction of n-decane/O2/Ar187
5 展望和挑战
本文综述了燃烧反应动力学的研究现状和存在的主要问题,介绍了基元反应的热、动力学参数和输运参数计算方法、复杂燃烧反应机理的构建和简化、燃烧反应机理在燃烧数值模拟中的应用、化学反应与湍流的相互作用以及燃烧测量和燃烧诊断方法。燃烧反应的支链反应特点,决定了燃烧反应的高度复杂性,所以无论是从科学层面还是应用层面,燃烧反应动力学研究都是一个长期的任务。
从最简单的氢-氧燃烧到石油基燃料、生物质燃料和火炸药,反应的微观机制涉及到大量的基础科学问题,这些问题包括自由基反应、电子态系间交叉、中间体的电子跃迁、非绝热反应等问题。在应用方面,一个可靠的、以基元步骤列表来表示的燃烧机理,需要解决两大问题,一是复杂反应网络的完整性,二是反应参数和流动参数的可靠性,这也正是燃烧反应基础研究的难点所在。如果在复杂燃烧反应机理中考虑电子激发态参与的反应步骤,问题将变得更为复杂。此外、压力相关速率常数的理论计算、低温条件下燃料点火延迟的负温度系数效应、高温条件下动力学计算中的非谐振校正,都是燃烧反应机理构建中需要引起重视的问题。
结合特定的反应器模型,基于燃烧反应机理的宏观动力学模拟可以预测燃烧实验数据(如点火延迟、火焰传播速度和物种浓度变化历史),反之实验验证对机理及其热、动力学数据的计算精度提出了更高的要求。近年来高精度量子化学方法和反应速率理论的发展使得热、动力学数据的精确计算成为可能,但是多参考电子结构方法,大分子体系动力学参数的精确计算方法的发展,速率常数的压力相关性,燃烧反应的非绝热过程,双自由基、激发态自由基以及燃烧低温氧化反应的动力学计算仍是将来研究的重点。
高温燃烧机理,尤其是C0–C4小分子核心机理,经过几十年国内外许多课题组的广泛研究,已经相对成熟,人们不断发现燃烧反应中的反应类型并引入燃烧机理构建。随着人们对低温燃烧现象的进一步认识,低温燃烧复杂机理近几年逐渐引起重视。但是,由于大量低稳定性的过氧化物种的引入,使得低温燃烧的机理构建变得庞大而困难,低温燃烧中占主体的含氧物种(醇类、醚类、酯类、酸类和醛酮类物种)的反应机理和动力学相关研究也还有待开展。大分子体系(> C10)的动力学参数大多数是采用反应类估算,这些动力学数据误差大,但其准确性对点火延迟和火焰传播速度的模拟结果的影响相对较小,因为在点火和火焰传播中,小分子自由基起着主要的作用。然而,要对燃烧过程给出可靠描述,如中间体浓度的演变历史,大分子燃烧反应参数的精确性还有大量工作要做。计算方法和技术条件还未能达到对燃烧机理作准确描述的水平。
燃烧机理的主要应用方向是燃烧数值模拟,特别是在发动机内流道等情况下,化学反应和湍流的相互作用变得非常复杂,采用计算流体力学(CFD)对发动机进行数值模拟时需要将化学反应和控制方程耦合进行求解,而详细的反应机理会使得计算量过于庞大。此外,由于各个物种及其涉及的反应特征时间尺度差异巨大,会给计算带来刚性问题。因此为了得到可靠的模拟结果,就必须在保证机理模拟精度的条件下发展更为精确有效的系统简化方法。
可以期望,随着计算方法的改进和计算手段的快速进步,从微观层面上,探明燃烧过程的反应通道、电子热激发机制和化学发光原理、自由基生成和猝灭、反应过程的系间窜越等,量子化学界将起作越来越重要的作用。在宏观方面,燃烧反应和湍流的相互作用机理研究和湍流燃烧的高保真三维数值模拟等领域的进展将在燃烧的高效利用和发动机预先设计等方面发挥不可替代的作用。
Supporting Information: available free of charge via the internet at http://www.whxb.pku.edn.cn.
(1)Ranzi, E.; Frassoldati, A.; Grana, R.; Cuoci, A.; Faravelli, T.;Kelley, A. P.; Law, C. K. Prog. Energy Combust. Sci. 2012, 38(4), 468.
(2)Yao, M. F.; Zheng, Z. L.; Liu, H. F. Prog. Energy Combust. Sci. 2009, 35 (5), 398. doi: 10.1016/j.pecs.2009.05.001
(3)Pilling, M. J. Proc. Combust. Inst. 2009, 32 (1), 27. doi: 10.1016/j.proci.2008.08.003
(4)Simmie, J. M. Prog. Energy Combust. Sci. 2003, 29 (6), 599. doi: 10.1016/S0360-1285(03)00060-1
(5)Battin-Leclerc, F.; Blurock, E.; Bounaceur, R.; Fournet, R.;Glaude, P. A.; Herbinet, O.; Sirjean, B.; Warth, V. Chem. Soc. Rev. 2011, 40 (9), 4762. doi: 10.1039/c0cs00207k
(6)Pilling, M. J. Chem. Soc. Rev. 2008, 37 (4), 676. doi: 10.1039/b715767c
(7)de Vijver, R. V.; Vandewiele, N. M.; Bhoorasingh, P. L.;Slakman, B. L.; Khanshan, F. S.; Carstensen, H. H.; Reyniers, M. F.; Marin, G. B.; West, R. H.; Van Geem, K. M. Int. J. Chem. Kinet. 2015, 47 (4), 199.
(8)Ruscic, B. Active Thermochemical Tables (ATcT), Version 1.112, http://atct.anl.gov/Thermochemical (2014)
(9)David, R. L. CRC Handbook of Chemistry and Physics, 89th Ed. (Internet version 2009); CRC Press/Taylor and Francis: Boca Raton, FL.
(10)Goldsmith, C. F.; Magoon, G. R.; Green, W. H. J. Phys. Chem. A 2012, 116 (36), 9033. doi: 10.1021/jp303819e
(11)Burke, S. M.; Simmie, J. M.; Curran, H. J. J. Phys. Chem. Ref. Data 2015, 44 (1), 013101. doi: 10.1063/1.4902535
(12)Goos, E.; Burcat, A.; Ruscic, B. New NASA Thermodynamic Polynomials Database with Active Thermochemical Tables updates, Report ANL 05/20 TAE 960, 2011.
(13)Benson, S. W. Thermochemical Kinetics: Methods for the Estimation of Thermochemical Data and Rate Parameters;Wiley: New York, 1976.
(14)Lay, T. H.; Bozzelli, J. W.; Dean, A. M.; Ritter, E. R. J. Phys. Chem. 1995, 99 (39), 14514. doi: 10.1021/j100039a045
(15)Ritter, E. R.; Bozzelli, J. W. Int. J. Chem. Kinet. 1991, 23 (9), 767.
(16)Muller, C.; Michel, V.; Scacchi, G.; Côme, G. M. J. Chim. Phys. 1995, 92, 1154.
(17)Ranzi, E.; Dente, M.; Faravelli, T.; Pennati, G. Combust. Sci. Techol. 1993, 95 (1–6), 1.
(18)Jencks, W. P. Chem. Rev. 1985, 85 (6), 511. doi: 10.1021/cr00070a001
(19)Sharma, S.; Raman, S.; Green, W. H. J .Phys. Chem. A 2010,114 (18), 5689. doi: 10.1021/jp9098792
(20)Miyoshi, A. J. Phys. Chem. A 2011, 115 (15), 3301. doi: 10.1021/jp112152n
(21)Evans, M. G; Polanyi, M. Trans. Faraday Soc. 1938, 34, 11. doi: 10.1039/tf9383400011
(22)Dean, A. M.; Bozzelli, J. W. Gas-phase Combustion Chemistry;Gardiner, W. C. Ed.; Springer-Verlag; New York: 2000.
(23)Harding, L. B.; Klippenstein, S. J.; Jasper, A. W. Phys. Chem. Chem. Phys. 2007, 9 (31), 4055. doi: 10.1039/b705390h
(24)Klippenstein, S. J.; Pande, V. S.; Truhlar, D. G. J. Am. Chem. Soc. 2014, 136 (2), 528. doi: 10.1021/ja408723a
(25)Vereecken, L.; Glowacki, D. R.; Pilling, M. J. Chem. Rev. 2015,115 (10), 4063. doi: 10.1021/cr500488p
(26)Pople, J. A.; Head-Gordon, M.; Raghavachari, K. J. Chem. Phys. 1987, 87 (10), 5968. doi: 10.1063/1.453520
(27)Purvis, G. D.; Bartlett, R. J. J. Chem. Phys. 1982, 76 (4), 1910. doi: 10.1063/1.443164
(28)Raghavachari, K.; Trucks, G. W.; Pople, J. A.; Head-Gordon, M. Chem. Phys. Lett. 1989, 157 (6), 479. doi: 10.1016/S0009-2614(89)87395-6
(29)Pople, J. A.; Head-Gordon, M.; Fox, D. J.; Raghavachari, K.;Curtiss, L. A. J. Chem. Phys. 1989, 90 (10), 5622. doi: 10.1063/1.456415
(30)Curtiss, L. A.; Raghavachari, K.; Redfern, P. C.; Rassolov, V.;Pople, J. A. J. Chem. Phys. 1998, 109 (18), 7764. doi: 10.1063/1.477422
(31)Curtiss, L. A.; Redfern, P. C.; Raghavachari, K.; Pople, J. A. J. Chem. Phys. 2001, 114 (1), 108. doi: 10.1063/1.1321305
(32)Curtiss, L. A.; Redfern, P. C.; Raghavachari, K. J. Chem. Phys. 2007, 126 (8), 084108. doi: 10.1063/1.2436888
(33)Petersson, G. A.; Bennett, A.; Tensfeldt, T. G.; Al-Laham, M. A.; Shirley, W. A.; Mantzaris, J. J. Chem. Phys. 1988, 89 (4), 2193. doi: 10.1063/1.455064
(34)Petersson, G. A.; Tensfeldt, T. G.; Montgomery, J. A. J. Chem. Phys. 1991, 94 (9), 6091. doi: 10.1063/1.460448
(35)Montgomery, J. A.; Ochterski, J. W.; Petersson, G. A. J. Chem. Phys. 1994, 101 (7), 5900. doi: 10.1063/1.467306
(36)Ochterski, J. W.; Petersson, G. A.; Montgomery, J. A. J. Chem. Phys. 1996, 104 (7), 2598. doi: 10.1063/1.470985
(37)Montgomery, J. A.; Frisch, M. J.; Ochterski, J. W.; Petersson, G. A. J. Chem. Phys. 1999, 110 (6), 2822. doi: 10.1063/1.477924
(38)Martin, J. M. L.; de Oliveira, G. J. Chem. Phys. 1999, 111 (5), 1843. doi: 10.1063/1.479454
(39)Boese, A. D.; Oren, M.; Atasoylu, O.; Martin, J. M. L.; Kállay, M.; Gauss, J. J. Chem. Phys. 2004, 120 (9), 4129. doi: 10.1063/1.1638736
(40)Karton, A.; Rabinovich, E.; Martin, J. M. L.; Ruscic, B. J. Chem. Phys. 2006, 125 (14), 144108. doi: 10.1063/1.2348881
(41)Karton, A.; Martin, J. M. L. J. Chem. Phys. 2012, 136 (12), 124114. doi: 10.1063/1.3697678
(42)Tajti, A.; Szalay, P. G.; Csaszár, A. G.; Kállay, M.; Gauss, J.;Valeev, E. F.; Flowers, B. A.; Vazquez, J.; Stanton, J. F. J. Chem. Phys. 2004, 121 (23), 11599. doi: 10.1063/1.1811608
(43)Bomble, Y. J.; Vazquez, J.; Kállay, M.; Michauk, C.; Szalay, P. G.; Csaszár, A. G.; Gauss, J.; Stanton, J. F. J. Chem. Phys. 2006, 125 (6), 064108. doi: 10.1063/1.2206789
(44)East, A.; Johnson, C.; Allen, W. J. Chem. Phys. 1993, 98 (2), 1299. doi: 10.1063/1.464298
(45)Schuurman, M. S.; Muir, S. R.; Allen, W. D.; Schaefer, H. F. J. Chem. Phys. 2004, 120 (24), 11586. doi: 10.1063/1.1707013
(46)Alecu, I. M.; Zheng, J. J.; Zhao, Y.; Truhlar, D. G. J. Chem. Theory Comput. 2010, 6 (9), 2872. doi: 10.1021/ct100326h
(47)Laury, M. L.; Boesch, S. E.; Haken, I.; Sinha, P.; Wheeler, R. A.; Wilson, A. K. J. Comput. Chem. 2011, 32 (11), 2339.
(48)Merrick, J. P.; Moran, D.; Radom, L. J. Phys. Chem. A 2007,111 (45), 11683. doi: 10.1021/jp073974n
(49)Raghavachari, K.; Trucks, G. W.; Pople, J. A.; Head-Gordon, M. Chem. Phys. Lett. 1989, 157 (6), 479. doi: 10.1016/S0009-2614(89)87395-6
(50)Simmie, J. M.; Somers, K. P. J. Phys. Chem. A 2015, 119 (28), 7235. doi: 10.1021/jp511403a
(51)Somers, K. P.; Simmie, J. M. J. Phys. Chem. A 2015, 119 (33), 8922. doi: 10.1021/acs.jpca.5b05448
(52)Ditchfield, R.; Hehre, W. J.; Pople, J. A.; Radom, L. Chem. Phys. Lett. 1970, 5 (1), 13. doi: 10.1016/0009-2614(70)80116-6
(53)Hehre, W. J.; Ditchfield, R.; Radom, L.; Pople, J. A. J. Am. Chem. Soc. 1970, 92 (16), 4796. doi: 10.1021/ja00719a006
(54)Ramabhadran, R. O.; Raghavachari, K. J. Chem. Theory Comput. 2011, 7 (7), 2094. doi: 10.1021/ct200279q
(55)Ramabhadran, R. O.; Raghavachari, K. J. Phys. Chem. A 2012,116 (28), 7531. doi: 10.1021/jp301421a
(56)Melius, C. F.; Binkley, J. S. Symp. (Int.) Combust. 1988, 21 (1), 1953. doi: 10.1016/S0082-0784(88)80432-6
(57)Melius, C. F.; Allendorf, M. D. J. Phys. Chem. A 2000, 104(11), 2168. doi: 10.1021/jp9914370
(58)Wilcox, C.; Russo, S. Int. J. Chem. Kinet. 2001, 33 (12), 770.
(59)Wu, J. M.; Zhou, Y. W.; Xu, X. Int. J. Quantum Chem. 2015,115 (16), 1021. doi: 10.1002/qua.24919
(60)Liu, C. X.; Wang, H. X.; Li, Z. R.; Rao, H. B.; Zhou, C. W.; Li, X. Y. J. Comput. Chem. 2010, 31 (14), 2585. doi: 10.1002/jcc.v31:14
(61)Zádor, J.; Taatjes, C. A.; Fernandes, R. X. Prog. Energy Combust. Sci. 2011, 37 (4), 371. doi: 10.1016/j.pecs.2010.06.006
(62)Carr, R. W. Modeling of Chemical Reactions; Green, N. J. B. Ed.; Elsevier B. V.; Amsterdam: 2007.
(63)Zhang, S.; Truong, T. N. J. Phys. Chem. A 2003, 107 (8), 1138. doi: 10.1021/jp021265y
(64)Bankiewicz, B.; Huynh, L. K.; Ratkiewicz, A.; Truong, T. N. J. Phys. Chem. A 2009, 113 (8), 1564. doi: 10.1021/jp808874j
(65)Orrego, J. F.; Truong, T. N.; Mondragon, F. J. Phys. Chem. A 2008, 112 (36), 8205. 36 doi: 10.1021/jp805012f
(66)Davis, A. C.; Francisco, J. S. J. Phys. Chem. A 2011, 115 (14), 2966. doi: 10.1021/jp110142h
(67)Davis, A. C.; Francisco, J. S. J. Phys. Chem. A 2010, 114 (43), 11492. doi: 10.1021/jp1042393
(68)Wang, H. X.; Wang, B. Y.; Zhang, J. L.; Li, Z. R.; Li, X. Y. Chem. J. Chin. Univ. 2011, 32 (5), 1123. [王海霞, 汪必耀, 张俊玲, 李泽荣, 李象远. 高等学校化学学报, 2011, 32 (5), 1123.]
(69)Wang, B. Y.; Tan, N. X.; Yao, Q.; Li, Z. R.; Li, X. Y. Acta Phys. -Chim. Sin. 2012, 28 (12), 2824. [汪必耀, 谈宁馨, 姚倩, 李泽荣, 李象远. 物理化学学报, 2012, 28 (12), 2824.] doi: 10.3866/PKU.WHXB201209053
(70)Wang, B. Y.; Li, Z. R.; Tan, N. X.; Yao, Q.; Li, X. Y. J. Phys. Chem. A 2013, 117 (16), 3279. doi: 10.1021/jp400924w
(71)Gilbert, R. G.; Smith, S. C. Theory of Unimolecular and Recombination Reactions; Blackwell: London, 1990.
(72)Jasper, A. W.; Miller, J. A.; Klippenstein, S. J. J. Phys. Chem. A 2013, 117 (47), 12243. doi: 10.1021/jp409086w
(73)Miller, J. A.; Klippenstein, S. J. J. Phys. Chem. A 2013, 117(13), 2718. doi: 10.1021/jp312712p
(74)Kim, S. K.; Ross, J. J. Chem. Phys. 1967, 46 (2), 818.
(75)Troe, J. J. Chem. Phys. 1977, 66 (11), 4758. doi: 10.1063/1.433838
(76)Sutton, G. P. History of Liquid Propellant Rocket Engines;American Institute of Aeronautics and Astronautics: Reston, Virginia, 2006.
(77)Jasper, A. W.; Miller, J. A. Combust. Flame 2014, 161 (1), 101.
(78)Cambi, R.; Cappelletti, D.; Liuti, G.; Pirani, F. J. Chem. Phys. 1991, 95 (3), 1852. doi: 10.1063/1.461035
(79)Barker, J. R.; Yoder, L. M.; King, K. D. J. Phys. Chem. A 2001,105 (5), 796. doi: 10.1021/jp002077f
(80)Jasper, A. W.; Pelzer, K. M.; Miller, J. A.; Kamarchik, E.;Harding, L. B.; Klippenstein, S. J. Science 2014, 346 (6214), 1212. doi: 10.1126/science.1260856
(81)Allen, J. W.; Goldsmith, C. F.; Green, W. H. Phys. Chem. Chem. Phys. 2012, 14 (3), 1131. doi: 10.1039/C1CP22765C
(82)Njegic, B.; Gordon, M. S. J. Chem. Phys. 2008, 129 (16), 164107. doi: 10.1063/1.2987712
(83)Johnson, R. D., III; Irikura, K. K.; Kacker, R. N.; Kessel, R. J. Chem. Theory Comput. 2010, 6 (9), 2822. doi: 10.1021/ct100244d
(84)Bowan, J. M. J. Chem. Phys. 1978, 68 (2), 608. doi: 10.1063/1.435782
(85)Neugebaur, J.; Hess, B. A. J. Chem. Phys. 2003, 118 (16), 7215. doi: 10.1063/1.1561045
(86)Pitzer, K. S.; Gwinn, W. D. J. Chem. Phys. 1942, 10 (7), 428. doi: 10.1063/1.1723744
(87)Van Speybroeck, V.; Van Neck, D.; Waroquier, M. J. Phys. Chem. A 2002, 106 (38), 8945. doi: 10.1021/jp025836y
(88)Vansteenkiste, P.; Van Speybroeck, V.; Marin, G. B.;Waroquier, M. J. Phys. Chem. A 2003, 107 (17), 3139. doi: 10.1021/jp027132u
(89)Klippenstein, S. J. Comprehensive Chemical Kinetics: Unimolecular Kinetics Part 1. The Reaction Step; Green, N. J. B. Ed.; Elsevier; Amsterdam: 2003.
(90)Li, Q.; Yao, L.; Shao, Y.; Yang, K. J. Chin. Chem. Soc. 2014,61 (3), 309. doi: 10.1002/jccs.v61.3
(91)Zhang, L. W.; Yao, L.; Lia, Q.; Wang, G. Q.; Lin, S. H. Mol. Phys. 2014, 112 (21), 2853. doi: 10.1080/00268976.2014.915066
(92)Li, Q.; Yao, L.; Lin, S. H. Can. J. Chem. 2015, 93 (6), 655. doi: 10.1139/cjc-2015-0005
(93)Song, D.; Su, H. M.; Kong, F. A.; Lin, S. H. J. Chem. Phys. 2013, 138 (10), 104301. doi: 10.1063/1.4794152
(94)Wigner, E. P. Z. Phys. Chem. Abt. B 1932, 19, 203.
(95)Eckart, C. Phys. Rev. 1930, 35 (2), 1303.
(96)Lu, D. H.; Truong, T. N.; Melissas, V. S.; Lynch, G. C.; Liu, Y. P.; Garrett, B. C.; Steckler, R.; Isaacson, A. D.; Rai, S. N.;Hancock, G. C.; Lauderdale, J. G.; Joseph, T.; Truhlar, D. G. Comput. Phys. Commun. 1992, 71 (3), 235. doi: 10.1016/0010-4655(92)90012-N
(97)Liu, Y. P.; Lynch, G. C.; Truong, T. N.; Lu, D. H.; Truhlar, D. G.; Garrett, B. C. J. Am. Chem. Soc. 1993, 115 (6), 2408. doi: 10.1021/ja00059a041
(98)Fernandez-Ramos, A.; Truhlar, D. G. J. Chem. Phys. 2001, 114(4), 1491. doi: 10.1063/1.1329893
(99)Docquier, N.; Lacas, F.; Candel, S. Proc. Combust. Inst. 2000,28 (2), 1765. doi: 10.1016/S0082-0784(00)80578-0
(100)Dandy, D. S.; Vosen, S. R. Combust. Sci. Techol. 1992, 82(1–6), 131.
(101)Walsh, K. T.; Long, M. B.; Tanoff, M. A.; Smooke, M. D. Proc. Combust. Inst. 1998, 27 (1), 615. doi: 10.1016/S0082-0784(98)80453-0
(102)Sherrill, C. D.; Leiniger, M. L.; van Huis, T. J.; Schaefer, H. F., III. J. Chem. Phys. 1988, 108 (3), 1040.
(103)Liu, X. J.; Bian, W. S.; Zhao, X.; Tao, X. T. J. Chem. Phys. 2006, 125 (7), 074306. doi: 10.1063/1.2263769
(104)Kern, R. D.; Chen, H.; Kiefer, J. H.; Mudipalli, P. S. Combust. Flame 1995, 100 (1–2), 177.
(105)Blitz, M. A.; Beasley, M. S.; Pilling, M. J.; Robinson, S. H. Phys. Chem. Chem. Phys. 2000, 2 (4), 805. doi: 10.1039/a907959i
(106)Bourig, A.; Thévenin, D.; Martin, J. P.; Janiga, G.; Zähringer, K. Proc. Combust. Inst. 2009, 32 (2), 3171. doi: 10.1016/j.proci.2008.09.004
(107)Dagdigian, P. J. Combust. Flame 2015, 162 (6), 2480. doi: 10.1016/j.combustflame.2015.02.016
(108)Brown, N. J.; Bastien, L. A. J.; Price, P. N. Prog. Energy Combust. Sci. 2011, 37 (5), 565. doi: 10.1016/j.pecs.2010.12.001
(109)Esposito, G.; Sarnacki, B. G.; Chelliah, H. K. Combust. Theory Model. 2012, 16 (6), 1029. doi: 10.1080/13647830.2012.700406
(110)Esposito, G.; Chelliah, H. K. Combust. Flame 2012, 159 (12), 3522. doi: 10.1016/j.combustflame.2012.07.009
(111)Grcar, J. F.; Bell, J. B.; Day, M. S. Proc. Combust. Inst. 2009,32 (1), 1173. doi: 10.1016/j.proci.2008.06.075
(112)Paul, P.; Warnatz, J. Symp. (Int.) Combust. 1998, 27 (1), 495. doi: 10.1016/S0082-0784(98)80439-6
(113)Middha, P.; Yang, B. H.; Wang, H. Proc. Combust. Inst. 2002,29 (1), 1361. doi: 10.1016/S1540-7489(02)80167-5
(114)Brown, N. J.; Revzan, K. L. Int. J. Chem. Kinet. 2005, 37 (9), 538.
(115)Chapman, S.; Cowling, T. G. The Mathematical Theory of Nonuniform Gases, 3rd ed.; Cambridge University Press: Cambridge, 1970.
(116)Côme, G. M.; Warth, V.; Glaude, P. A.; Fournet, R.; Battin-Leclerc, F.; Scacchi, G. Symp. (Int.) Combust. 1996, 26 (1), 755.
(117)Warth, V.; Battin-Leclerc, F.; Fournet, R.; Glaude, P. A.; Côme, G. M.; Scacchi, G. Comput. Chem. 2000, 24 (5), 541.
(118)Battin-Leclerc, F.; Glaude, P. A.; Warth, V.; Fournet, R.;Scacchi, G.; Côme, G. M. Chem. Eng. Sci. 2000, 55 (15), 2883.
(119)Kirchner, F. Atmos. Environ. 2005, 39 (6), 1143. doi: 10.1016/j.atmosenv.2004.09.086
(120)Junier, M.; Kirchner, F.; Clappier, A.; van den Bergh, H. Atmos. Environ. 2005, 39 (6), 1161. doi: 10.1016/j.atmosenv.2004.09.085
(121)Vandewiele, N. M.; Van Geem, K. M.; Reyniers, M. F.; Marin, G. B. Chem. Eng. J. 2012, 207–208, 526.
(122)Susnow, R. G.; Dean, A. M.; Green, W. H.; Peczak, P.;Broadbelt, L. J. J. Phys. Chem. A 1997, 101 (20), 3731. doi: 10.1021/jp9637690
(123)Herbinet, O.; Biet, J.; Hakka, M. H.;Warth, V.; Glaude, P. A.;Nicolle, A.; Battin-Leclerc, F. Proc. Combust. Inst. 2011, 33(1), 391. doi: 10.1016/j.proci.2010.07.060
(124)Green, W. H.; Allen, J. W.; Ashcraft, R. W.; Beran, G. J.; Class, C. A.; Gao, C.; Goldsmith, C. F.; Harper, M. R.; Jalan, A.;Magoon, G. R.; Matheu, D. M.; Merchant, S. S.; Mo, J. D.;Petway, S.; Raman, S.; Sharma, S.; Song, J.; van Geem, K. M.;Wen, J.; West, R. H.; Wong, A.; Wong, H. S.; Yelvington, P. E.; Yu, J. 2013. RMG-Reaction Mechanism Generator v4.0 which can be found online: http://rmg.sourceforge.net/.
(125)Green, W. H.; Barton, P. I.; Bhattacharjee, B.; Matheu, D. M.;Schwer, D. A.; Song, J.; Sumathi, R.; Carstensen, H. H.; Dean, A. M.; Grenda, J. M. Ind. Eng. Chem. Res. 2001, 40 (23), 5362. doi: 10.1021/ie001088s
(126)Song, J.; Stephanopoulos, G.; Green, W. H. Chem. Eng. Sci. 2002, 57 (21), 4475
(127)http: //www.frad.t.u-tokyo.ac.jp/%7emiyoshi/KUCRS/
(128)Ranzi, E.; Faravelli, T.; Gaffuri, P.; Sogaro, A.; D'Anna, A.; Ciajolo, A. Combust. Flame 1997, 108 (1–2), 24.
(129)Faravelli, T.; Bua, L.; Frassoldati, A.; Antifora, A; Tognotti, L.;Ranzi, E. Comput. Chem. Eng. 2001, 25 (4–6), 613.
(130)Chevalier, C.; Warnatz, J.; Melenk, H.; Bunsen-Ges, B. Phys. Chem. 1990, 94, 1362.
(131)Baulch, D. L.; Cobos, C. J.; Cox, R. A.; Frank, P.; Hayman, G.;Just, T.; Kerr, J. A.; Murrells, T.; Pilling, M. J.; Troe, J.;Walker, R. W.; Warnatz, J. J. Phys. Chem. Ref. Data 1994, 23(6), 847. doi: 10.1063/1.555953
(132)Rasmussen, C. L.; Hansen, J.; Marshall, P.; Glarborg, P. Int. J. Chem. Kinet. 2008, 40 (8), 454. doi: 10.1002/kin.v40:8
(133)Rasmussen, C. L.; Jakobsen, J. G.; Glarborg, P. Int. J. Chem. Kinet. 2008, 40 (12), 778. doi: 10.1002/kin.v40:12
(134)Alzueta, M. U.; Gao, Y.; Marshall, P.; Glarborg, P. Proc. Combust. Inst. 2009, 32 (1), 367. doi: 10.1016/j.proci.2008.06.188
(135)Smith, G. P.; Golden, D. M.; Frenklach, M.; et al. http://www.me.berkeley.edu/gri_mech/.
(136)Walker, R. W.; Morley, C. Basic Chemistry of Combustion. In Low-Temperature Combustion and Autoignition; Pilling, M. J. Ed.; Elsevier: Amsterdam, The Netherlands, 1997; pp 1–124.
(137)Westbrook, C. K.; Pitz, W. J.; Herbinet, O.; Curran, H. J.; Silke, E. J. Combust. Flame 2009, 156 (1), 181. doi: 10.1016/j.combustflame.2008.07.014
(138)Zhang, C. H.; Li, P.; Guo, J. J.; Li, X. Y. Energy Fuels 2012, 26(2), 1107. doi: 10.1021/ef201611a
(139)Zhang, K. W.; Banyon, C; Togbé, C.; Dagaut, P.; Bugler, J.;Curran, H. J. Combust. Flame 2015, 162 (11), 4194. doi: 10.1016/j.combustflame.2015.08.001
(140)Merchant, S. S.; Goldsmith, C. F.; Vandeputte, A. G.; Burke, M. P.; Klippenstein, S. J.; Green, W. H. Combust. Flame 2015,162 (10), 3658. doi: 10.1016/j.combustflame.2015.07.005
(141)Ranzi, E.; Cavallotti, C.; Cuoci, A.; Frassoldati, A.; Pelucchi, M.; Faravelli, T. Combust. Flame 2015, 162 (5), 1679.
(142)Herbinet, O.; Husson, B.; Serinyel, Z.; Cord, M.; Warth, V.;Fournet, R.; Glaude, P. A.; Sirjean, B.; Battin-Leclerc, F.;Wang, Z. D.; Xie, M. F.; Cheng, Z. J.; Qi, F. Combust. Flame 2012, 159 (12), 3455. doi: 10.1016/j.combustflame.2012.07.008
(143)Sayle, R. J. Chem. Inf. Model. 2009, 49 (3), 519. doi: 10.1021/ci800243w
(144)Bone, R. G. A.; Firth, M. A.; Sykes, R. A. J. Chem. Inf. Comput. Sci. 1999, 39 (5), 846. doi: 10.1021/ci990422w
(145)Daylight Theory Manual. http://www.daylight.com/dayhtml/doc/theory/theory.toc.html
(146)McKay, B. D. Congr. Numerantium 1981, 30, 45.
(147)Weininger, D.; Weininger, A.; Weininger, J. L. J. Chem. Inf. Comput. Sci. 1989, 29 (2), 97. doi: 10.1021/ci00062a008
(148)Faulon, J. L.; Collins, M. J.; Carr, R. D. J. Chem. Inf. Comput. Sci. 2004, 44 (2), 427. doi: 10.1021/ci0341823
(149)Braun, J.; Gugisch, R.; Kerber, A.; Laue, R.; Meringer, M.;Rücker, C. J. Chem. Inf. Comput. Sci. 2004, 44 (2), 542. doi:10.1021/ci030404l
(150)Morgan, H. L. J. Chem. Doc. 1965, 5 (2), 107. doi: 10.1021/c160017a018
(151)Ehrlich, H. C.; Rarey, M. WIREs Comput. Mol. Sci. 2011, 1 (1), 68. doi: 10.1002/wcms.v1.1
(152)Guo, J. J.; Hua, X. X.; Wang, F.; Tan, N. X.; Li, X. Y. Acta Phys. -Chim. Sin. 2014, 30 (6), 1027. [郭俊江, 华晓筱, 王 繁,谈宁馨, 李象远. 物理化学学报, 2014, 30 (6), 1027.] doi: 10.3866/PKU.WHXB201404031
(153)Garner, S.; Sivaramakrishnan, R.; Brezinsky, K. Proc. Combust. Inst. 2009, 32 (1), 461. doi: 10.1016/j.proci.2008.06.217
(154)Malewicki, T.; Gudiyella, S.; Brezinsky, K. Combust. Flame 2013, 160 (1), 17. doi: 10.1016/j.combustflame.2012.09.013
(155)Xu, J. Q.; Guo, J. J.; Liu, A. K.; Wang, J. L.; Tan, N. X.; Li, X. Y. Acta Phys. -Chim. Sin. 2015, 31 (4), 643. [徐佳琪, 郭俊江,刘爱科, 王健礼, 谈宁馨, 李象远. 物理化学学报, 2015, 31 (4), 643.] doi: 10.3866/PKU.WHXB201503022
(156)Ning, H. B.; Gong, C. M.; Li, Z. R.; Li, X. Y. J. Phys. Chem. A 2015, 119 (18), 4093. doi: 10.1021/acs.jpca.5b02013
(157)Ning, H. B.; Gong, C. M.; Tan, N. X.; Li, Z. R.; Li, X. Y. Combust. Flame 2015, 162 (11), 4167. doi: 10.1016/j.combustflame.2015.08.004
(158)Lu, T. F.; Law, C. K. Proc. Combust. Inst. 2005, 30 (1), 1333. doi: 10.1016/j.proci.2004.08.145
(159)Pepiot-Desjardins, P.; Pitsch, H. Combust. Flame 2008, 154(1–2), 67.
(160)Niemeyer, K. E.; Sung, C. J.; Raju, M. P. Combust. Flame 2010, 157 (9), 1760. doi: 10.1016/j.combustflame.2009.12.022
(161)Sun, W. T.; Chen, Z.; Gou, X. L.; Ju, Y. G. Combust. Flame 2010, 157 (7), 1298. doi: 10.1016/j.combustflame.2010.03.006
(162)Liu, A. K.; Jiao, Y.; Li, S. H.; Wang, F.; Li, X. Y. Energy Fuels 2014, 28 (8), 5426. doi: 10.1021/ef5002502
(163)Zhong, B. J.; Yao, T.; Wen, F. Acta Phys. -Chim. Sin. 2014, 30(2), 210. [钟北京, 姚 通, 文 斐. 物理化学学报, 2014, 30(2), 210.] doi: 10.3866/PKU.WHXB201312103
(164)Vervisch, L.; Poinsot, T. Annu. Rev. Fluid Mech. 1998, 30, 655. doi: 10.1146/annurev.fluid.30.1.655
(165)Lesieur, M.; Metais, O. Annu. Rev. Fluid Mech. 1996, 28, 45. doi: 10.1146/annurev.fl.28.010196.000401
(166)Snider, D. M.; Clark, S. M.; O'Rourke, P. J. Chem. Eng. Sci. 2011, 66 (6), 1285. doi: 10.1016/j.ces.2010.12.042
(167)Brenner, D. W. Phy. Rev. B 1990, 42 (15), 9458. doi: 10.1103/PhysRevB.42.9458
(168)van Duin, A. C. T.; Dasgupta, S.; Lorant, F.; Goddard, W. A., III. J. Phys. Chem. A 2001, 105 (41), 9396. doi: 10.1021/jp004368u
(169)Chenoweth, K.; van Duin, A. C. T.; Goddard, W. A., III. J. Phys. Chem. A 2008, 112 (5), 1040. doi: 10.1021/jp709896w
(170)Wang, Q. D.; Hua, X. X.; Cheng, X. M.; Li, J. Q.; Li, X. Y. J. Phys. Chem. A 2012, 116 (15), 3794. doi: 10.1021/jp300059a
(171)Wang, Q. D.; Wang, J. B.; Li, J. Q.; Tan, N. X.; Li, X. Y. Combust. Flame 2011, 158 (2), 217. doi: 10.1016/j.combustflame.2010.08.010
(172)Cheng, X. M.; Wang, Q. D.; Li, J. Q.; Wang, J. B.; Li, X. Y. J. Phys. Chem. A 2012, 116 (40), 9811. doi: 10.1021/jp304040q
(173)Aldén, M.; Bood, J.; Li, Z. S.; Richter, M. Proc. Combust. Inst. 2011, 33 (1), 69. doi: 10.1016/j.proci.2010.09.004
(174)Li, Y. Y.; Qi, F. Accounts Chem. Res. 2010, 43 (1), 68. doi: 10.1021/ar900130b
(175)Qi, F. Proc. Combust. Inst. 2013, 34 (1), 33. doi: 10.1016/j.proci.2012.09.002
(176)Hansen, N.; Klippenstein, S. J.; Taatjes, C. A.; Miller, J. A.;Wang, J.; Cool, T. A.; Yang, B.; Yang, R.; Wei, L. X.; Huang, C. Q.; Wang, J.; Qi, F.; Law, M. E.; Westmoreland, P. R. J. Phys. Chem. A 2006, 110 (10), 3670.
(177)Yang, B.; Huang, C. Q.; Wei, L. X.; Wang, J.; Sheng, L. S.;Zhang, Y. W.; Qi, F.; Zheng, W. X.; Li, W. K. Chem. Phys. Lett. 2006, 423 (4–6), 321.
(178)Tian, Z. Y.; Li, Y. Y.; Zhang, T. C.; Zhu, A. G.; Cui, Z. F.; Qi, F. Combust. Flame 2007, 151 (1–2), 347.
(179)Savee, J. D.; Papajak, E.; Rotavera, B.; Huang, H. F.; Eskola, A. J.; Welz, O.; Sheps, L.; Taatjes, C. A.; Zádor, J.; Osborn, D. L. Science 2015, 347 (6222), 643. doi: 10.1126/science.aaa1495
(180)Sung, C. J.; Curran, H. J. Prog. Energy Combust. Sci. 2014, 44, 1. doi: 10.1016/j.pecs.2014.04.001
(181)Hanson, R. K.; Davidson, D. F. Prog. Energ. Combust. Sci. 2014, 44, 103. doi: 10.1016/j.pecs.2014.05.001
(182)Zhu, Y. Y.; Li, S. J.; Davidson, D. F.; Hanson, R. K. Proc. Combust. Inst. 2015, 35 (1), 241. doi: 10.1016/j.proci.2014.05.034
(183)Rao, F.; Li, B.; Li, P.; Zhang, C. H.; Li, X. Y. Energy Fuels 2014, 28 (11), 6707.
(184)Zhang, C. H.; Li, B.; Rao, F.; Li, P.; Li, X. Y. Proc. Combust. Inst. 2015, 35 (3), 3151. doi: 10.1016/j.proci.2014.05.017
(185)Clifford, E. P.; Farrell, J. T.; DeSain, J. D.; Taatjes, C. A. J. Phys. Chem. A 2000, 104 (49), 11549. doi: 10.1021/jp0024874
(186)Knepp, A. M.; Meloni, G.; Jusinski, L. E.; Taatjes, C. A.;Cavallotti, C.; Klippenstein, S. J. Phys. Chem. Chem. Phys. 2007, 9 (31), 4315. doi: 10.1039/b705934e
(187)Wang, L. D.; Li, P.; Zhang, C. H.; Tang, H. C.; Ye, B.; Li, X. Y. Spectrosc. Spect. Anal. 2012, 32 (5), 1166. [王利东, 李 萍,张昌华, 唐洪昌, 叶 彬, 李象远. 光谱学与光谱分析, 2012,32 (5), 1166.]
Progress in Combustion Kinetics
NING Hong-Bo1LI Ze-Rong2LI Xiang-Yuan1,*
(1College of Chemical Engineering, Sichuan University, Chengdu 610065, P. R. China;2College of Chemistry, Sichuan University, Chengdu 610064, P. R. China)
Chemical kinetic modeling has become more and more important in the analysis of combustion systems. Considerable progress has been made in the development of combustion models in recent years. This review includes the following contents: electronic structure methods for combustion kinetics, recent developments on the calculation methods of thermodynamic parameters and rate constants in combustion, developments of combustion mechanisms and reduction techniques, molecular simulations with reactive force fields, combustion intermediate measurements, experiments for ignition delay time with shock wave tubes and combustion diagnostics. Due to the extreme complexity of reaction networks, the combustion mechanism is still not clearly understood by researchers. Owing to the strong application background, the combustion kinetics have attracted attention in recent years. The solver for reaction rate of intermediate species during combustion occupies the central point in combustion simulation. The progress in the research on reactionturbulence interactions, and the combination of combustion kinetics with computational fluid dynamics, will facilitate fuel design and combustion simulation. To build a reliable combustion model for achieving a reasonable flow field structure description of engines is another important aspect.
Hydrocarbons; Combustion reaction; Pressure-dependency; Combustion mechanism; Combustion diagnostics
O643
10.3866/PKU.WHXB201512151
Received: October 16, 2015; Revised: December 14, 2015; Published on Web: December 15, 2015.
*Corresponding author. Email: xyli@scu.edu.cn; Tel: +86-28-85405233.
The project was supported by the National Natural Science Foundation of China (91441114, 91441132).
国家自然科学基金(91441114, 91441132)资助项目
©Editorial office of Acta Physico-Chimica Sinica
