螺旋槽液膜密封端面空化发生机理

李振涛，郝木明，杨文静，曹恒超，任宝杰



螺旋槽液膜密封端面空化发生机理

李振涛，郝木明，杨文静，曹恒超，任宝杰

（中国石油大学（华东）密封技术研究所，山东青岛 266580）

液膜中空化的发生直接影响着密封流体动压润滑性能，基于质量守恒的JFO边界条件，建立考虑表面粗糙度的螺旋槽液膜密封物理模型，经坐标变换将不规则物理域转换成规则计算域，采用有限控制体积法离散控制方程并求解，分析了膜厚、表面粗糙度、螺旋槽功用（上游泵送和下游泵送）、螺旋槽开槽位置及空化压力对液膜中空化发生的影响。结果表明：较小膜厚工况易促生空穴，而较大膜厚易削弱空穴，且随着膜厚增大，表面粗糙度的影响降低甚至被忽略；当密封为上游泵送型时，空穴区周向宽度明显大于下游泵送型，而螺旋槽位置对空化的影响与螺旋槽功用密切相关；选取较小空化压力使空穴缩减，而较大者反之，且后者对提升液膜承载有利。

液膜密封；空化机理；上游泵送；下游泵送；空化压力

引 言

液膜润滑非接触式机械密封（简称“液膜密封”）因其具有可实现工艺介质零泄漏或零逸出、改善密封摩擦副润滑状态和提高系统稳定性等显著特点[1]，在工程中得到广泛应用，其中以螺旋槽液膜密封最为典型。因功用不同，液膜密封又可分为上游泵送[2]和下游泵送[3]两种类型。在实际运转过程中，液膜密封因楔效应和挤压效应的存在，密封端面间液膜处于受挤压和剪切状态，易促使发生空化[4]。由于空化的产生对密封端面间液膜稳态特性、润滑状态及密封系统可靠性等产生较大影响[5-6]，使其成为液膜密封技术发展中的关注焦点。

针对空化问题，Swift[7]和Stieber[8]提出Swift-Stieber边界条件（即Reynolds边界条件），该边界条件应用最广但无法正确解释破裂液膜再形成的过程。为解决上述问题及确保边界条件满足质量守恒，Jakobsson等[9]和Olsson[10]随后提出一种空化边界，即JFO边界条件。Elrod[11]为实现JFO边界条件，基于有限差分法，得到可实现自动追踪空化边界的空化算法。之后，Kumar等[12]，Vijayaraghavan等[13]分别对Elrod算法不断进行改进和修正。而Fesanghary等[14]提出一种新的开关算法，可进一步提高Elrod算法的稳定性和收敛速度。目前，国内外学者对液膜密封空化问题研究取得了较多成果，但主要集中于对密封端面空化试验观察及影响分析，如Khonsari等[15]对激光加工多孔端面微造型的空化进行可视化试验并进行性能分析；李京浩[16]对机械密封空化效应进数值分析及试验研究；郝木明等[17-18]研究了空化效应对螺旋槽液膜密封的稳态特性及波锥度对密封空化特性影响，而对螺旋槽液膜密封空化发生机理无相关报道。

为有效采取措施控制螺旋槽液膜密封中空化的发生及分布，有必要对液膜中空化发生机理进行深入研究。因此，本文基于满足质量守恒的JFO边界条件，深入探究液膜厚度、表面粗糙度、螺旋槽开槽位置和功用（上游泵送和下游泵送）及空化压力等因素对液膜中空化发生机理的影响，为完善液膜密封理论设计及结构优化提供可靠依据。

1 数学模型

1.1 物理模型

图1所示为考虑表面粗糙度的螺旋槽液膜密封摩擦副结构，由配对的旋转环和静止环组成。因旋转环表面上螺旋槽的存在，工作时摩擦副间的液体处于流体动力润滑状态；其中，流体动压部分由台区和槽区交错组成，而流体静压部分由坝区（单坝区或双坝区）组成。

在图1所示摩擦副中，i和o分别表示密封面的内半径和外半径；g表示内径开槽型（简称“内槽式”）液膜密封的槽根半径；g1和g2分别表示中间开槽型（简称“中槽式”）液膜密封的内槽根半径和外槽根半径；i和o分别表示内、外半径处压力；和sc分别表示单周期的起始角和周期角；为螺旋槽角；L和G分别为台区和槽区对应的圆周角度，在本文中，定义L/G=1。

为方便区分及讨论内槽式和中槽式两种情况，定义=(g1−i)/(o−g)。当=0时，表示内槽式；>0，表示中槽式。同时，定义内外径压差为=o−i，根据图1所示旋转环的旋转方向，当>0时，密封为上游泵送型；当<0时，密封为下游泵送型。

图1所示的物理模型中内槽式液膜密封的几何结构参数与操作工况参数如表1中的工况1所述。

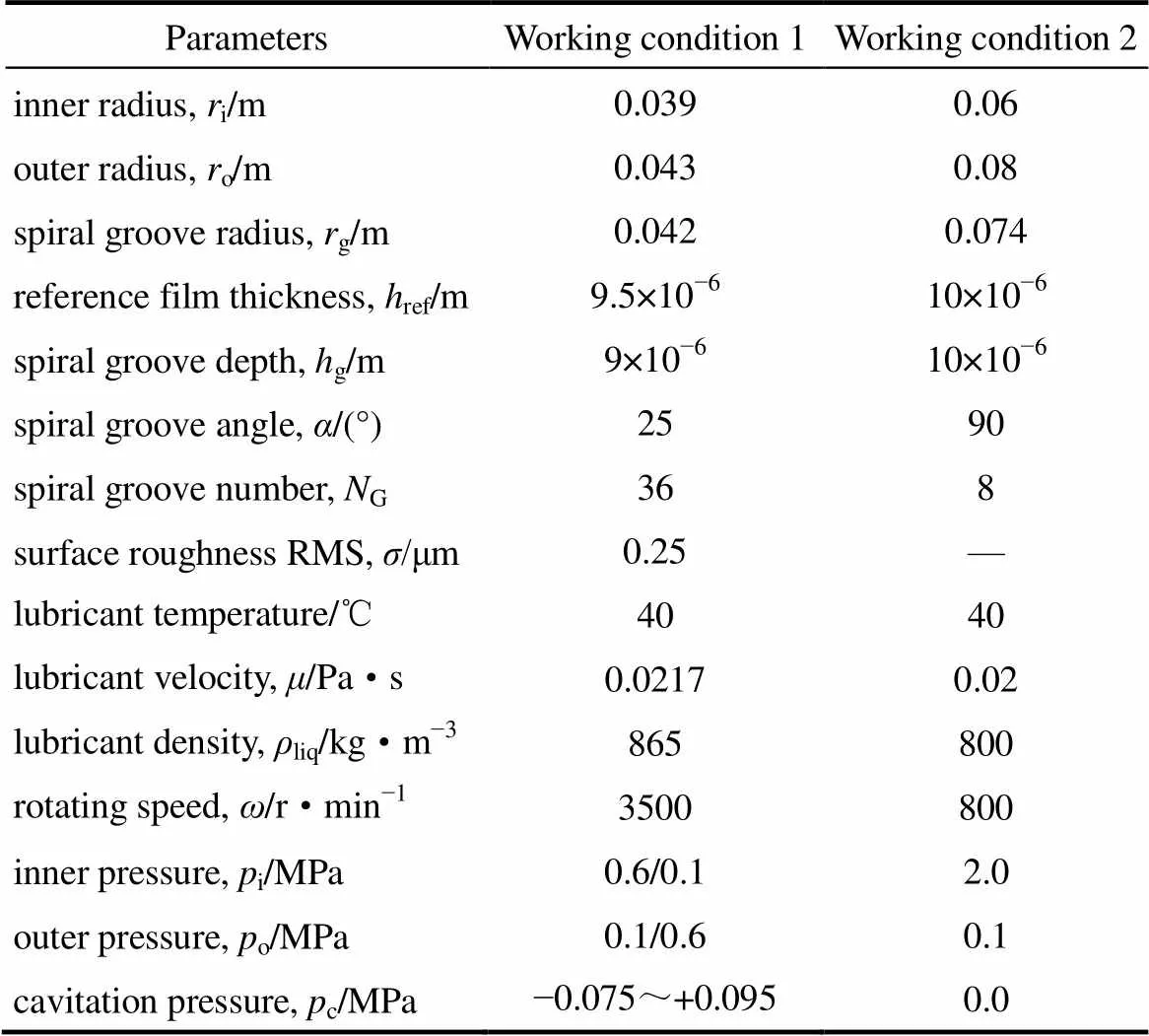
表1 液膜密封几何结构与工况参数

Note: ① For downstream pumping seals,i/o: 0.6 MPa /0.1 MPa;

② For upstream pumping seals,i/o: 0.1 MPa /0.6 MPa.

1.2 计算域及基本假设

以内槽式液膜密封为例，选取两条对数螺旋线和内、外半径处的圆弧包络的计算域，即由一个槽区、左右两个半台区和一个坝区组成的区域定义为单周期计算域，如图1(a)所示。因密封端面结构的对称性，其他区域与之相应位置具有相同的液膜膜厚分布和压力分布。

为便于后续确定密封摩擦副间液膜控制方程及简化数值计算，对计算域数学模型做如下假设：

（1）润滑液体为牛顿流体，层流状态且黏度不随压力变化；

（2）润滑薄膜分为全液膜区和空穴区，前者区域流体为不可压缩，而后者区域压力保持不变；

（3）忽略密封流体的热楔效应及摩擦副的热变形，且忽略除离心力外的惯性项的影响[19]；

（4）旋转环和静止环具有相同的表面粗糙度，且表面粗糙度满足具有各向同性的高斯概率分布；

（5）摩擦副间液膜处于等温状态，不考虑温度变化。

2 控制方程与数值求解

2.1 控制方程

基于假设，稳态工况下考虑粗糙度影响的质量守恒平均流量控制方程在极坐标中的形式[20-21]

式中，Φ、Φ和Φ分别表示径向压力流量因子、周向压力流量因子和剪切流量因子。当三者分别满足Φ=1.0，Φ=1.0，Φ=0，则式(1)变换为适用于光滑平面的Reynolds方程。

当式(1)计算的局部压力低于摩擦副间润滑液体在工况温度下的饱和蒸气压时，液膜中会产生空穴[22]。空穴区主要是由气相和液相组成的两相混合物，压力设定为空化压力，即c；而密度为气液两相混合物的平均密度，即。JFO模型不仅描述了液膜破裂位置边界（与Reynolds模型相同），而且也确定了液膜再形成位置边界；因此，为实现该模型在数值计算中自动捕捉液膜破裂和再形成边界，引入通用变量和空化数，两参数满足：

全液膜区

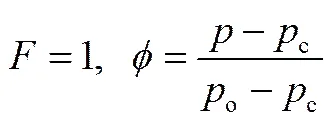
空穴区

(3)

将式(2)、式(3)代入式(1)并进行量纲1化处理，得到控制方程

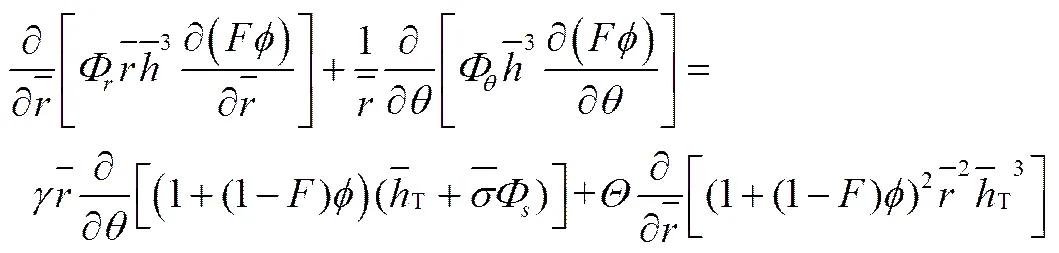
式中，量纲1化参量为

，，，，，，

2.2 坐标变换

因螺旋槽液膜密封的计算域不规则，为提高采用有限体积法进行离散求解的收敛性，采用坐标变换方法[23]将不规则的物理域变换为规则的计算域，坐标变换函数为式(5)

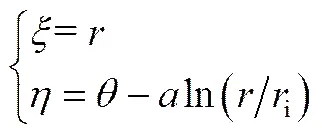
式中，=1/tan。

经坐标变换后，新坐标系中的单周期计算域如图2所示。

在新坐标系中，式(4)经变换后的形式为

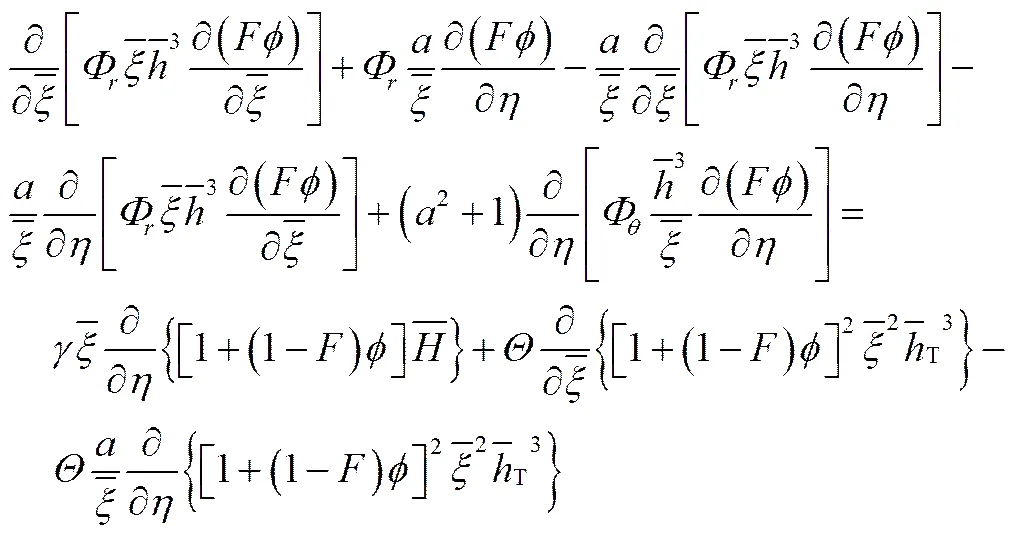
相应地，初始边界条件和周期性边界条件分别为式(7)和式(8)

(8)

2.3 膜厚方程

不考虑表面粗糙度时，密封摩擦副非槽区对应的两光滑平面间名义膜厚为=ref，而槽区名义膜厚为=ref+g，如图1(b)所示。考虑表面粗糙度后，由其决定的随机膜厚T为

式中，为两表面粗糙度的综合均方根偏差[24]。

2.4 数值求解

2.4.1 离散化 新坐标系下计算域内局部区域网格划分及以P为中心节点的控制体积如图3所示。图中n、s、w、e分别代表和方向的有限体积边界，而W、E、N、S、WN、WS、EN、ES分别代表与中心节点P相邻的8个节点。

在控制体积中，沿w→e，角度步长为Δ；沿s→n，量纲1化半径步长为。采用有限体积法对式(6)进行整体积分并离散，整理得式(10)

对式(10)进一步整理，得控制体积中心节点P处通用变量的代数方程式，如式(11)

(11)

式中，各变量表示如下

，，，

，

，

，，

，

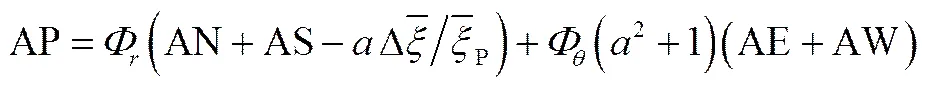
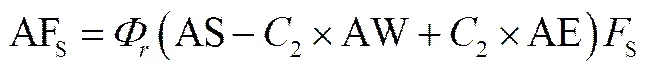
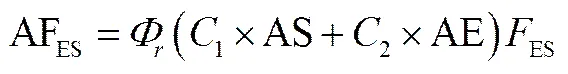
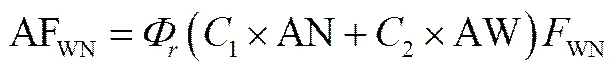
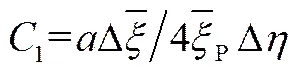
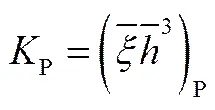
式中，下角标代表n、s、e、w；下角标分别对应代表N、S、E、W。

2.4.2 迭代求解 为进一步提高迭代速度并保证良好的收敛性，采用Gauss-Seidel迭代方法对式(11)进行求解，并引入松弛因子和，对每一步计算的和进行迭代更新[25]，以消除P项中和的二次非线性项的影响。

迭代更新方程为

(13)

式中，变量关系如下

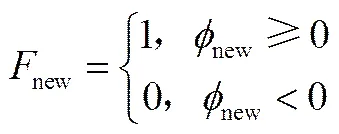
迭代收敛判别准则为

(15)

迭代收敛后，可获得计算域内通用变量和空化数的分布。进而可求解整个计算域内液膜压力、承载能力z及体积泄漏量Q，具体公式如下

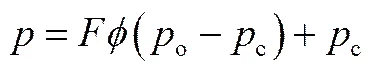
(17)

(18)

3 计算结果与分析

3.1 程序算法验证

由于螺旋槽液膜密封摩擦副间的液膜处于微米级，通过试验直接观察密封端面空化发生、分布情况及直接测量摩擦副间周向液膜压力难度较大，本文拟分别采用摩擦副间泄漏量试验测量结果和周向液膜压力数值试验方法对程序算法进行验证。

首先是密封端面间泄漏量数值计算值与试验测量值对比。试验工装，如图4所示。试验中，密封摩擦副具体几何参数（除膜厚外）和工况参数见表1中的工况1内容所述。

图4(a)中①和②分别表示旋转环和静止环，且对应于图4(c)、(d)所示的实物图。采用JFO模型的数值计算方法获得的不同转速下的密封端面泄漏量与试验测量值对比结果，如图5所示。

由图5可知，由于数值算法的假设及实际试验的复杂性，采用的空化模型数值算法得到的端面泄漏量与试验实测值不可避免存在一定误差，但两者总体吻合较好，从而证明该算法的正确性。

为更好地验证本文的空化模型及其用于进行螺旋槽液膜密封端面空穴发生机理的分析，以刘丁华等[26]中的工况参数（如表1中工况2内容）为例，将本文数值算法及分别采用JFO模型和Reynolds模型计算所得结果与文献中的压力分布曲线进行对比，如图6所示。由图可知：本文数值算法获得的压力分布与文献结果十分吻合，证明了本文程序算法的准确性。进一步分析，可知相对于Reynolds模型所得的压力曲线，JFO模型更好地诠释了空化液膜开始破裂和再形成的边界，可以很好地用于螺旋槽液膜密封空化发生机理的分析。

3.2 液膜破裂和再形成位置分析

相对于不考虑空化，空化的发生影响着螺旋槽液膜密封端面液膜产生的流体动压润滑特性。为进一步完善液膜密封流体动压润滑机理及液膜分布机理，以密封摩擦副间润滑介质的压力或密度变化为判据，以液膜开始破裂和再形成边界为目标，从影响其变化的因素分析空化发生机理。

参考表1中工况1的参数，根据网格划分无关性检测标准（保证前后两次误差控制在0.1%），确定了计算域内沿周向和径向的总网格数分别为80和60。计算域内各区网格划分详述，如图7所示。

图8为=1/2、>0时的液膜中空穴分布，图中黑框为中槽式密封螺旋槽边界线，空白处为空穴区，形状类似三角形。结合图1(a)可知：液膜破裂位置沿膜厚由右侧半台区向槽区发散方向，而开始破裂位置位于螺旋槽右边界前缘处；液膜再形成位置沿膜厚由槽区向左侧半台区收敛方向，定义液膜开始破裂半径方向的两端为液膜再形成的起始端，而沿周向最大圆周角处液膜再形成位置为液膜再形成的终止端。为方便分析，将后者简称为液膜再形成位置。

3.2.1 液膜厚度和表面粗糙度的影响 液膜密封为流体动压型，密封面最小间隙大于2 μm[27]，而在工程设计中确保其稳定运行时端面间隙为10 μm左右。考虑粗糙度后，膜厚比（即ref/）需大于3～5，可确保密封运行在流体动压状态[28]。为此，在该部分选取两个参考膜厚：3 μm和9.5 μm，以分析液膜厚度和表面粗糙度对空化的影响。图9、图10分别所示为=0、<0、不同参考膜厚和粗糙表面时，量纲1化半径`=1.04处沿周向的通用变量分布。

由图9、图10可知：膜厚为3 μm和9.5 μm时，液膜开始破裂位置相同，均位于膜厚发散位置；同时，压力峰值均发生在螺旋槽膜厚收敛位置。但膜厚为3 μm时，空穴沿周向的宽度显著大于膜厚为9.5 μm时，使液膜再形成位置沿周向后延。这表明较小膜厚时，液膜因挤压加剧，流体动压能力的增强使得低压区沿周向范围增大，通用变量小于零的区域随之增加，空穴区增大。反之，膜厚较大时，空穴区减小。

相对于光滑平面，膜厚为3 μm时，表面粗糙度的变化并未影响液膜开始破裂位置且空穴沿周向宽度近乎相等；但较大表面粗糙度使液膜在再形成位置的压力梯度相对于较小表面粗糙度时逐渐变大，液膜的抵抗破裂能力增强；同时压力峰值亦增大。这是因为在该参考膜厚下，膜厚比约为3～6，表面粗糙度的作用不可忽略；结合式(9)可知，上述现象的产生主要是因随着表面粗糙度的增大，由其决定的随机膜厚反而逐渐减小，使得密封端面间流体动压润滑效应增强作用的结果。

当膜厚为9.5 μm时，膜厚比约为9.5～19，表面粗糙度的影响甚微。可以得出：随着膜厚增大，表面粗糙度对空穴分布及流体动压润滑性能的影响逐渐减弱甚至可以忽略不计，这与Patir等[28]的理论结果相一致。

3.2.2 螺旋槽位置和功用的影响 根据图8所示结果，分别绘制<0和>0、参考膜厚为9.5 μm（后面所讨论内容的参考膜厚均为9.5 μm，不再提及）、不同时，液膜开始破裂位置径向和液膜再形成位置周向的通用变量分布，详见图11～图14。

由图11、图12可知：通用变量由内径至外径呈先由正数区进入负数区，再进入正数区的变化趋势。在两图中的负数区各存在一个最小负值，分别为-0.278和-0.273。根据式(3)，最小负值处意味着该位置空化密度最小；经计算，两图中最小空化密度分别近似为624.53、628.86 kg·m-3。在负数区即液膜开始破裂位置中，空化密度最小处可被认为空化度最大，即径向液膜破裂源。由于进入槽区的液体流动方向（螺旋槽与右台区边界处液体相对于旋转环的运动方向，位于背风侧）及槽区与坝区边界的阻拦作用，使得液膜破裂源至内半径方向液膜再形成开始位置的通用变量梯度缓慢变化，而至外半径方向的梯度快速变化，使得空穴区更靠近内半径处。

当>0、=0时，内、外径两侧的液膜再形成起始位置相比<0、=0时的计算值，前者空穴的起始位置更靠近内径处，从变量值变化考虑，主要是因为压力偏低造成的；但两者外径处的起始位置基本相同。随着的增加，内坝区变量值均呈先增大后减小趋势且越大值峰值越大，使得内径处液膜再形成起始位置向外径方向偏移，当增大到一定值（如=3/4），内径处起始位置不再变化。相对于=0时，不同下外径处液膜再形成起始位置略微外移且位置基本相同。

由图13可知：当<0时，随着增加，空穴区周向宽度（即液膜再形成位置距开始破裂位置间的周向宽度）先增大后减小，并在=1/2时达到最大值，这表明中槽式密封相比内槽式可促进空化发生。因此，致使>0对应的液膜再形成位置的后缘处的值均比=0偏低；但随着周向角度的增大，值亦增大。当周向角度约为0.1 rad时，>0对应的值超过=0对应值并随周向角度增加继续增加，且峰值至超过1/2后不再变化。考虑空化后，<0、不同时对应承载能力如图15所示。由图可知，当=1/8时，承载能力最低，随着增加，承载能力先增大后减小，并在=1/2时达到最大值，与图13中的空化区周向宽度变化规律相似。

由图14可知：当>0时，随着的增加，空穴区周向宽度逐渐减小，但与图13计算结果相比，空穴区周向宽度仍明显增大，结合图11、图12中所示的两种情况下液膜开始破裂位置径向宽度基本相同，结果表明上游泵送型密封可促生空穴，而下游泵送密封削弱空穴。究其原因，是内外半径处压差引起的压差流和流体动压槽作用下的黏性剪切流共同作用，前者压差流和剪切流异向相减，流体动压作用减弱；后者两种流动同向相加，流体动压作用增强。

进一步分析，>0时液膜再形成位置后缘处的压力相对于=0时逐渐增大，且值峰值亦增大。考虑空化后，>0、不同时对应承载能力，如图15所示。由图可知，当=1/8时，承载能力最低，随着增加，承载能力呈现增大趋势，与图14中的空化区周向宽度变化规律相反。

3.2.3 空化压力的影响 密封摩擦副间润滑介质的空化压力即饱和蒸气压的选取，会直接影响到液膜中空化的分布以及液膜承载能力。但由于受润滑介质的纯度，周围环境的压力、温度及湿度等因素影响，润滑介质的空化压力选取较为困难。

图16、图17分别绘制了<0和>0，=1/2时，不同空化压力时沿`=1.04处的周向压力分布曲线。

由16、图17可知：空化压力的增加，使液膜开始破裂位置前缘处的全液膜区压力略微升高，但是对液膜再形成位置后缘处全液膜区压力影响甚微。相比空穴压力为0时，随着空穴压力负压绝对值的增大，空穴区周向宽度减小；而随着空穴压力正压的增大，空穴区周向宽度增加。

图18所示<0和>0、=1/2时，不同空化压力对液膜承载能力的影响。由图可知：随着空化压力的增加，不论<0还是>0，液膜承载能力均呈现近似线性增加趋势。这表明空化压力的增加在一定程度上有助于提升承载能力。

4 结 论

（1）基于满足质量守恒的JFO空化模型，以计算域润滑介质压力或密度为判据，清晰阐述了螺旋槽液膜密封端面空穴发生的机理，为完善液膜密封理论设计及结构优化奠定良好基础。

（2）液膜密封因螺旋槽的存在，在槽内液体流动的背风侧即膜厚发散处，液膜开始破裂；随着液体在槽内向迎风侧流动即膜厚收敛方向，液膜自开始破裂半径方向的两端开始再形成过程，并至液膜再形成终止位置构成完整空穴区。

（3）液膜密封端面空穴发生与螺旋槽功用和位置密切相关。密封为上游泵送型时，空穴区周向宽度明显大于下游泵送型，而中槽式密封的空穴区周向宽度亦大于内槽式密封，且随内坝区增大，空穴区周向宽度增大并在内外坝区径向宽度相等时达最大；密封为下游泵送型时，中槽式密封的空穴区宽度小于内槽式密封，且随内坝区增大，空穴区周向宽度逐渐减小。

（4）本文对密封端面空穴机理的研究是建立在等温定黏度基础上，以压力或密度为判据，未考虑黏度变化。后续将开展以黏度变化为判据进行空化机理分析。

符 号 说 明

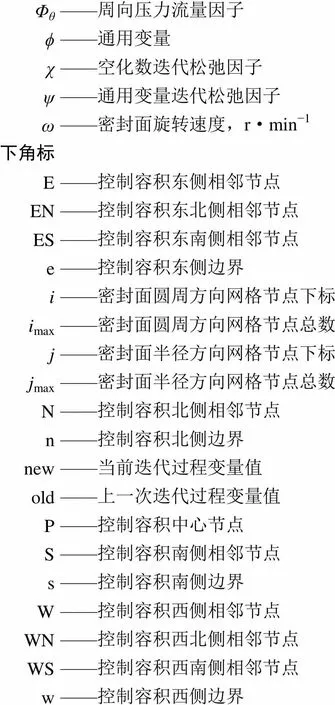
F——空化数 h——密封面间隙总膜厚，m hg——槽区膜厚，m href——参考膜厚，m hT——表面粗糙度决定的随机膜厚，m `h——量纲1密封面间隙总膜厚 `hT——量纲1表面粗糙度决定的随机膜厚 NG——螺旋槽数目 p——密封面间隙液膜压力 pc——空化压力，MPa pi——密封面内径处压力，MPa po——密封面外径处压力，MPa Qr——密封面径向体积泄漏量，L·min−1 Ra——表面粗糙度算术平均，μm Re*——密封面间隙流体Reynolds数 r——(r, θ)坐标系下密封面半径，m rg——(r, θ)坐标系下螺旋槽根半径，m rg1——(r, θ)坐标系下内槽式密封内槽根半径，m rg2——(r, θ)坐标系下内槽式密封外槽根半径，m ri——(r, θ)坐标系下密封面内半径，m ro——(r, θ)坐标系下密封面外半径，m `r——(r, θ)坐标系下量纲1密封面半径 Wz——液膜承载能力，N α——螺旋槽角，(°) γ——密封面间隙流体过程系数 Δ——密封面内外径处压力差，MPa Δξ——(ξ, η)坐标系下半径步长，m Δ`ξ——(ξ, η)坐标系下量纲1半径步长 η——(ξ, η)坐标系下圆周角，rad ηG——(ξ, η)坐标下计算域圆周角，rad ηi——(ξ, η)坐标下计算域起始角，rad Θ——量纲1数 θ——(r, θ)坐标系下圆周角，rad θG——(r, θ)坐标系下计算域内径处槽区圆周角，rad θi——(r, θ)坐标系下计算域起始角，rad θL——(r, θ)坐标系下计算域内径处台区圆周角，rad θsc——(r, θ)坐标系下计算域圆周角，rad λ——内坝区比例，定义为(rg1−ri)/(ro−rg) μ——密封面间隙流体动力黏度，Pa·s ξ——(ξ, η)坐标下密封面半径，m ξi——(ξ, η)坐标下密封面内半径，m ξo——(ξ, η)坐标下密封面外半径，m `ξ——(ξ, η)坐标下量纲1半径 ρ——空化区气液混相平均密度，kg·m−3 ρliq——密封面间隙流体密度，kg·m-3 σ——表面粗糙度综合均方根偏差，μm Φr——径向压力流量因子 Φs——剪切流量因子 Φθ——周向压力流量因子 ϕ——通用变量 χ——空化数迭代松弛因子 ψ——通用变量迭代松弛因子 ω——密封面旋转速度，r·min−1 下角标 E——控制容积东侧相邻节点 EN——控制容积东北侧相邻节点 ES——控制容积东南侧相邻节点 e——控制容积东侧边界 i——密封面圆周方向网格节点下标 imax——密封面圆周方向网格节点总数 j——密封面半径方向网格节点下标 jmax——密封面半径方向网格节点总数 N——控制容积北侧相邻节点 n——控制容积北侧边界 new——当前迭代过程变量值 old——上一次迭代过程变量值 P——控制容积中心节点 S——控制容积南侧相邻节点 s——控制容积南侧边界 W——控制容积西侧相邻节点 WN——控制容积西北侧相邻节点 WS——控制容积西南侧相邻节点 w——控制容积西侧边界

References

[1] 郝木明, 李振涛, 任宝杰, 等. 机械密封技术及应用[M]. 2版. 北京: 中国石化出版社, 2014: 76-78. HAO M M, LI Z T, REN B J,. Mechanical Seal Technology and Application [M]. 2nd ed. Beijing: China Petrochemical Press, 2014: 76-78.

[2] 郝木明, 胡丹梅, 郭洁. 新型上游泵送机械密封的性能研究[J]. 化工机械, 2001, 28(1): 12-15. HAO M M. HU D M, GUO J. Performance study of the new upstream pumping mechanical seal [J]. Chemical Machinery, 2001, 28(1): 12-15.

[3] 王玉明. 下游泵送双列螺旋槽端面密封: 2307157Y [P]. 1999-02-10. WANG Y M. Downstream pumping double spiral groove face seal: 2307157Y [P]. 1999-02-10.

[4] 王涛, 黄伟峰, 王玉明. 机械密封液膜汽化问题研究现状及进展[J]. 化工学报, 2012, 63(11): 3375-3382. DOI: 10.3969/j.issn.0438- 1157.2012.11.001. WANG T, HUANG W F, WANG Y M. Research and progress of mechanical seals operating with vaporization transition [J]. CIESC Journal, 2012, 63(11): 3375-3382. DOI: 10.3969/j.issn.0438-1157. 2012.11.001.

[5] 陈汇龙, 吴强波, 左木子, 等. 机械密封端面液膜空化的研究进展[J]. 排灌机械工程学报, 2015, 33(2): 138-144. DOI: 10.3969/j.issn. 1674-8530.14.0085. CHEN H L, WU Q B, ZUO M Z,. Overview on liquid film cavitation in mechanical seal faces [J]. Journal of Drainage and Irrigation Machinery Engineering, 2015, 33(2): 138-144. DOI: 10.3969/j.issn.1674-8530.14.0085.

[6] 唐飞翔, 孟祥铠, 李纪云, 等. 基于质量守恒的Laser-Face液体润滑机械密封数值分析[J]. 化工学报, 2013, 64(10): 3694-3700. DOI: 10.3969/j.issn.0438-1157.2013.10.029. TANG F X, MENG X K, LI J Y,. Numerical analysis of Laser-Face liquid mechanical seal based on mass conservation [J]. CIESC Journal, 2013, 64(10): 3694-3700. DOI: 10.3969/j.issn. 0438-1157.2013.10.029.

[7] SWIFT H W. The stability of lubricating films in journal bearings [J]. Minutes of the Proceedings of the ICE, 1932, 233: 267-288. DOI: 10.1680/imotp.1932.13239.

[8] STIEBER W. Das Schwimmlager: Hydrodynamische Theorie des Gleitlagers[M]. Berlin: VDI Verlag, 1933.

[9] JAKOBSSON B, FLOBERG L. The finite journal bearing, considering vaporization [J]. Wear, 1958, 2(2): 85-88.

[10] OLSSON K O. Cavitation in dynamically loaded bearings [J]. Wear, 1967, 55(2): 295-304.

[11] ELROD H G. A cavitation algorithm [J]. Journal of Lubrication Technology, 1981, 103(3): 350-354. DOI: 10.1115/1.3251669.

[12] KUMAR A, BOOKER J F. A finite element cavitation algorithm [J]. Journal of Tribology, 1991, 113(2): 276-284. DOI: 10.1115/1. 2920617.

[13] VIJAYARAGHAVAN D, KEITH T G. Development and evaluation of a cavitation algorithm [J]. Tribology Transactions, 1989, 32(2): 225-233. DOI: 10.1018/10402008908981882.

[14] FESANGHARY M, KHONSARI M M. A modification of the switch function in the Elrod cavitation algorithm [J]. Journal of Tribology, 2011, 133(2): 024501. DOI: 10.1115/1.4003484.

[15] QIU Y, KHONSARI M M. On the prediction of cavitation in dimples using a mass-conservative algorithm [J]. Journal of Tribology, 2009, 131(4): 41702-41711.

[16] 李京浩. 机械密封空化效应的数值计算方法与试验研究[D]. 北京: 清华大学, 2011. LI J H. Numerical computational method and experimental study for cavitation in mechanical seals [D]. Beijing: Tsinghua University, 2013.

[17] 郝木明, 庄媛, 章大海, 等. 考虑空化效应的螺旋槽液膜密封特性数值研究[J]. 中国石油大学学报(自然科学版), 2015, 39(3): 132-137. DOI: 10.3969/j.issn.1673-5005.2015.03.018. HAO M M, ZHUANG Y, ZHANG D H,. Numerical study on sealing performance of spiral groove liquid film seal considering effects of cavitation [J]. Journal of China University of Petroleum, 2015, 39(3): 132-137. DOI: 10.3969/j.issn.1673-5005.2015.03.018.

[18] 李振涛, 郝木明, 杨文静, 等. 波度和锥度对液体润滑机械密封空化特性影响[J]. 化工学报, 2016, 67(5): 2005-2014. DOI: 10.11949/j.issn.0438-1157.20151733. LI Z T, HAO M M, YANG W J,. Effects of waviness and taper on cavitation characteristic of liquid lubricated mechanical seals [J]. CIESC Journal, 2016, 67(5): 2005-2014. DOI: 10.11949/j.issn. 0438-1157.20151733.

[19] YU T H, SADEGHI F. Groove effects on thrust washer lubrication[J]. Journal of Tribology, 2001, 123(2): 295-304. DOI: 10.1115/1. 1308014.

[20] 赵一民, 胡纪滨, 吴维, 等.螺旋槽旋转密封环润滑状态转变预测[J]. 机械工程学报, 2013, 49(9): 75-80. DOI: 10.3901/JME. 2013.09.075. ZHAO Y M, HU J B, WU W,. Prediction of lubrication condition transition for spiral groove rotary seal rings [J]. Journal of Mechanical Engineering, 2013, 49(9): 75-80. DOI: 10.3901/JME.2013.09.075.

[21] PINKUS O, LUND J W. Centrifugal effects in thrust bearings and seals under laminar conditions [J]. Transactions of the ASME, 1981, 103(1): 126-136. DOI: 10.1115/1.3251600.

[22] PAYVAR P, SALANT R F. A computational method for cavitation in a wavy mechanical seal [J]. Journal of Tribology, 1992, 114(1): 199-204. DOI: 10.1115/1.2920861.

[23] JAMES D D, POTTER A F. Numerical analysis of the gas-lubricated spiral-groove thrust bearing-compressor [J]. Journal of Lubrication Technology, 1967, 89(4): 439-443. DOI: 10.1115/1.3617023.

[24] LEBECK A O. Principles and Design of Mechanical Face Seals [M]. New York: John WileySons Inc., 1991: 53-58.

[25] XIONG S W, WANG J Q. Steady-state hydrodynamic lubrication modeled with the Payvar-Salant mass conservation model [J]. Journal of Tribology, 2012, 134: 031703. DOI: 10.1115/1.4006615.

[26] 刘丁华, 胡纪滨. 空化模型对径向直线槽端面密封性能分析的影响[J]. 北京理工大学学报, 2012, 32(11): 1101-1104. DOI: 10.15918/j.tbit1001-0645.2012.11.019.LIU D H, HU J B. Effect of cavitation model on the performance of radial grooved face seals [J]. Transactions of Beijing Institute of Technology, 2012, 32(11): 1101-1104. DOI: 10.15918/j.tbit1001- 0645.2012.11.019.

[27] 顾永泉. 机械端面密封[M]. 东营: 石油大学出版社, 1994: 3. GU Y Q. Mechanical Face Seal [M]. Dongying: China University of Petroleum Press, 1994: 3.

[28] PATIR N, CHENG H S. Application of average flow model to lubrication between rough sliding surfaces [J]. Journal of Lubrication Technology, 1979, 101(2): 220-229. DOI: 10.1115/1.3453329.

Cavitation mechanism of spiral groove liquid film seals

LI Zhentao, HAO Muming, YANG Wenjing, CAO Hengchao, REN Baojie

(Institute of Sealing Technology, China University of Petroleum, Qingdao 266580, Shandong, China)

Cavitation occurrence in liquid film has a direct impact on hydrodynamic lubrication performance of mechanical seals. A physical model of liquid film seal in spiral grooves was built with consideration of surface roughness and the JFO cavitation boundary condition on mass conservation. The anomalous physical domain composed of spiral curves was transformed into an inerratic computational domain by coordinate transformation. Finite control volume method was adopted to discretize the liquid film governing equation and the Gauss-Seidel relaxation iterative algorithm was used to solve the algebraic iterative equation. The cavitation occurrence in liquid film was analyzed by multiple factors of liquid film thickness, surface roughness, upstream/downstream pumping function, grooving position of spiral groove and cavitation pressure. Results show that cavitation occurrence was easily strengthened at thin films but weakened at thick films. Effects of surface roughness on cavitation or pressure distribution was depressed or even disappeared with increase of liquid film thickness. In case of upstream pumping seal, the circumferential width of cavitation was larger than that of downstream pumping seal, the width for middle grooving seal was larger than that of inner grooving seal, as well as the width enlargement with increase of inner dam reached to maximum when the radial width of inner dam was equal to that of outer dam. However, in case of downstream pumping seal, the width of middle grooving seal was smaller and decreased with increase of the inner dam. Effects of grooving position on cavitation were closely related to the function of spiral groove. Cavitation shranked at lower cavitation pressure but promoted at higher cavitation pressure. High cavitation pressure was beneficial to improving load-carrying capacity of the liquid film.

liquid film seals; cavitation mechanism; upstream pumping; downstream pumping; cavitation pressure

2016-05-30.

Prof. HAO Muming, haomm@upc.edu.cn

10.11949/j.issn.0438-1157.20160742

TH 117.2

A

0438—1157（2016）11—4750—12

李振涛（1983—），男，博士研究生。

国家自然科学基金项目（51375497）；山东省自主创新及成果转化专项项目（2014ZZCX10102-4）。

2016-05-30收到初稿，2016-06-23收到修改稿。

联系人：郝木明。

supported by the National Natural Science Foundation of China (51375497) and the Shandong Special Projects of Independent Innovation and Achievement Transformation (2014ZZCX10102-4).