翅片结构对双向开缝翅片管换热器性能的影响

屠琦琅，袁益超，胡晓红



翅片结构对双向开缝翅片管换热器性能的影响

屠琦琅，袁益超，胡晓红

（上海理工大学上海市动力工程多相流动与传热重点实验室，上海200093）

为了获得翅片结构对双向开缝翅片管换热器传热与阻力性能的影响规律，对不同翅片间距f和开缝高度h的双向开缝翅片管换热器进行了数值模拟，并对数值模拟结果进行了模化试验验证。结果表明：当<7200时，增大f会提高双向开缝翅片管换热器的传热与阻力性能；当>7200时，减小f会提高其传热性能，降低其阻力性能；随着h的增加，双向开缝翅片管换热器的传热性能先降低后提高，阻力性能先提高后降低；对于不同翅片结构的5种双向开缝翅片管换热器，f越大，综合流动传热性能越高，但实际换热面积会减小，需综合考虑；在=2734～6712范围内数值模拟与试验结果吻合较好，数值模拟能较准确地反映双向开缝翅片管换热器的传热与阻力特性。研究成果可为双向开缝翅片管换热器的结构与性能优化提供依据。

双向开缝翅片管换热器；传热；数值模拟；模化试验；综合流动传热性能；优化

引 言

翅片管换热器广泛应用于化工、电力以及空调与制冷等行业。气-液间壁式传热的主要热阻集中在气侧，占50%～70%[1]，所以应该强化气侧传热。气侧换热表面采用整体套片式的翅片管具有结构紧凑和传热效率高的特点。在整体套片式翅片管气侧平直翅片上开缝使其成为间断式翅片是进一步强化传热的一种有效方法[2-3]。由于翅片上的开缝结构增强了流体的扰动，破坏了翅片表面的流体边界层，从而有效减薄了边界层厚度，显著增强了传热[4]。近年来，国内外学者对开缝翅片管换热器进行了大量研究。Du等[5]研究了管排数对开缝翅片管换热器传热性能的影响。Yun等[6]对不同翅片间距、开缝高度、开缝数量等的双排开缝翅片管换热器进行了试验研究。Tang等[7]对螺旋翅片、平直翅片、开缝翅片、纵向涡发生器和混合型翅片等5种翅片管换热器进行了试验和数值模拟研究，并对纵向涡发生器进行了结构优化，使其传热性能优于开缝翅片。尹斌等[8]对3种不同型式的开缝翅片管换热器进行了数值模拟，发现双边交替开缝翅片的传热性能最好，单边开缝翅片的阻力最小。鹿钦礼等[9]对不同开缝形式的翅片管换热器进行了三维数值模拟，并用场协同理论进行分析，为工程实际运用提供了一定的理论指导。杨立军等[10]对6种不同管束结构的Forge型翅片管束和椭圆形翅片管束进行了试验及数值模拟研究，并得到了相关特征数关联式，对相关空冷系统的选型及运行具有指导意义。袁益超等[11-13]对不同结构的开缝翅片管换热器进行了试验和数值模拟研究，得到了运行工况以及翅片结构对开缝翅片管换热器传热与阻力性能的影响规律。

目前，对双向开缝翅片管换热器传热与阻力性能的研究还处在不断发展和完善的过程中，改变其结构参数以进一步提高其传热与阻力性能是研究的重点。翅片间距和开缝高度的不同会影响双向开缝翅片管换热器的换热面积和空气的扰动强度，且与改变管径、管间距以及开缝数量等方法相比，改变翅片间距和开缝高度相对较为方便[14]。合理的翅片间距和开缝高度可以使双向开缝翅片管换热器在较小的阻力增量范围内尽量提高换热性能，以达到强化传热以及节能的目的。

本文采用数值模拟与模化试验相结合的方法研究翅片间距及开缝高度对双向开缝翅片管换热器传热与阻力特性的影响规律，同时综合考虑其传热与阻力性能，以便为此类换热器的结构与性能优化提供依据。

1 数值计算模型

1.1 物理模型

本文研究的双向开缝翅片管换热器的翅片结构如图1所示，模化试验元件的主要结构参数见表1。

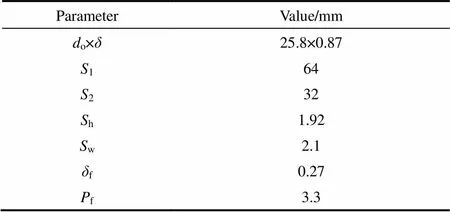
表1 试验元件主要结构参数

对整体的换热管束进行数值模拟需要庞大的计算容量，故通常选取能代表管束流动与传热特性的单元空间作为计算区域。考虑到双向开缝翅片管换热器几何结构的周期性和对称性，选取实际换热过程中一部分作为研究对象，如图2所示。该计算区域沿方向选取相邻两列管中心线之间的区域，沿方向选取两翅片中线之间的区域，沿方向选取空气流经的4排管子。为使得入口处空气速度均匀且垂直于入口截面，在入口处延长约3倍基管外径长度；在出口处延长约7倍基管外径长度，以保证出口无回流[15]。同时为了使模型更接近试验条件，得到更准确的结果，翅片上开缝的结构与实物完全相同。因工艺要求，本研究的双向开缝翅片管换热器基管与翅片之间有翻边结构，不过因翻边厚度很薄、紧贴基管表面，且翅片材质为导热性能优异的铝，故在数值模拟时忽略了此翻边结构，并认为此忽略不会对其流动和传热性能的变化趋势产生明显影响。用GAMBIT建立的开缝翅片三维模型如图3所示。

1.2 数学模型及数值模拟方法

本文采用Fluent软件对双向开缝翅片管换热器的流动与传热过程进行数值模拟。计算模型为三维稳态湍流不可压缩流动，数值模拟控制方程由连续性方程、动量守恒方程和能量守恒方程组成[16]，湍流模型选用标准-模型，压力与速度的耦合采用SIMPEL算法[17]。边界条件设置如图4所示：空气入口为速度入口，分别取7个不同的迎风面风速(1.0、1.3、1.5、1.7、1.9、2.1、2.3 m·s-1)；空气出口设为自由出流；基管和翅片表面均为无滑移壁面。空气入口温度统一设为25℃，基管内表面温度设为恒壁温58℃（参照本文试验时基管内循环水的平均温度），翅片表面为对流换热的流固耦合边界[18]；在方向上的边界为对称性边界条件；在方向上为周期性边界条件；换热管壁和翅片材料均为铝，并忽略管壁与翅片之间的接触热阻。

1.3 网格划分及无关性验证

由于所研究的双向开缝翅片管换热器结构的复杂性，特别是翅片的开缝结构，所以在划分网格的过程中采用分块及局部细化的方法。网格划分的基本原则为：翅片和基管表面的网格划分细密，流体区域的网格随着离翅片管表面距离的增大而趋于稀疏，以达到节省计算时间、提高计算精度的目的。对翅片、基管及流体区域均采用适应性较好的非结构化四面体网格。

为了得到网格的独立解，消除网格划分数目对模拟结果的影响，以试验元件结构参数为例进行网格无关性验证，对网格数目分别为420万、460万、520万的3个模型进行模拟，模拟结果表明和的变化均在3%以内，满足网格无关性要求。为了兼顾计算速度与精度，选取网格数目为460万的模型进行后续模拟。

1.4 数据处理方法

根据数值模拟结果可以得到模型的换热量、空气出口温度以及模型前后压差，从而可以计算出模型的Reynolds数、Nusselt数、Euler数以及摩擦因子。

Reynolds数

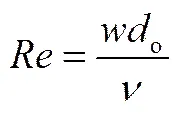
Nusselt数

(2)

Euler数

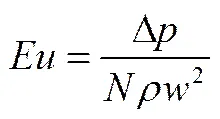
摩擦因子

(4)

式中，o为基管外径，m；o为管外空气侧对流传热系数，W·m-2·K-1；为管束间最小流通截面空气流速，m·s-1；为管外空气运动黏度，m2·s-1；为管外空气热导率，W·m-1·K-1；为管外空气密度，kg·m-3；为沿空气流动方向管排数；Δ为管外空气侧流动阻力，Pa；ca为空气流动方向的翅片长度，m。

1.5 模化试验验证

1.5.1 模化试验系统 为验证本文数值模拟方法的准确性，对表1所示双向开缝翅片管换热器试件的传热与阻力特性进行了模化试验。试验系统如图5所示。该系统包括4个部分：冷却空气系统、循环水系统、控制系统、数据采集系统。

1—air heater; 2—uniform flow field device; 3—thermocouple; 4—test element; 5—differential pressure transmitter; 6—nozzle box; 7—pressure transmitter; 8—induced draft fan; 9—electric motor; 10—water tank; 11—water heater; 12—pump; 13—valve; 14—electromagnetic flowmeter; 15—platinum resistor

冷却空气系统主要由空气电加热器、整流格栅、试验段、喷嘴流量箱和引风机组成；由引风机从外界环境中引入的空气，被电加热器加热到试验所需温度，沿风道经整流格栅，使流体流速分布均匀，到达试验段，横向冲刷双向开缝翅片管换热器。空气将管束内循环水的热量带走后进入喷嘴流量箱，最后经引风机排至外界环境，完成整个吸热过程。循环水系统主要由稳压水箱、水泵、电加热器、电磁流量计及试验段组成。循环水在稳压水箱中经电加热器加热到试验所需温度，由水泵从稳压水箱中引出，经电磁流量计后，进入试验段，被空气冷却后回到稳压水箱，完成循环。控制系统主要功能是通过实时监测、控制和调节水温、水速、风温、风速，以满足试验所需工况。

在试验过程中，当循环水放热量和空气吸热量之间的误差保持在±2%以内，认为试验工况已经稳定，即可采集数据。空气流量由喷嘴测量，试验段进、出口空气温度由经标定的铜-康铜热电偶网测量，空气侧压降由精度为0.2级的EJA-120A型差压变送器测量，进、出口水温由A级精度的Pt100铂电阻测量。水流量由精度为0.2级的AXF040G型电磁流量计测量。测量仪表的输出信号通过ADAM-4118型模块采集，经ADAM-4520型模块转换后，由计算机程序采集。

试验过程不可避免地存在误差。本试验的误差主要有试验段进口风温ai和出口风温ao的误差、试验段进出口水温降Δw的误差、水流量w的误差、空气流量a的误差、水侧放热量w的误差、空气侧吸热量a的误差以及传热系数的误差，根据试验参数及试验过程所涉及的仪表精度，由误差传递理论[19]可计算各参数的相对误差，见表2。

表2 各参数相对误差

1.5.2 数值模拟与模化试验结果的比较 本文模化试验工况为进口风温25℃，进口水温60℃，数值模拟与模化试验结果比较如图6所示。

由图可以看出，在=2734～6712时，数值模拟与模化试验的相对误差在9.6%以内，的相对误差在-3.28%～0.63%范围内，两者吻合较好。可见，本文采用的数值模拟方法能够较好地反映双向开缝翅片管换热器的传热与阻力特性。

导致数值模拟和模化试验结果之间误差的原因主要在于：①数值模拟所采用的计算模型是经过简化处理的，如采用对称性边界条件以减少网格数量、缩短计算时间，而试验时对应的对称面上不可能没有流体的交换；②数值模拟时管壁内表面温度设置为常数，而试验时管壁温度沿流程方向是变化的；③由于制造工艺水平，试验元件翅片及管壁表面存在着一定的粗糙度，且翅片与管壁之间有一定的接触热阻，而数值模拟的物理模型表面是绝对光滑的，且不考虑翅片与管壁之间的接触热阻。④试验系统及数值模拟本身存在一定的误差。

2 数值模拟结果与分析

鉴于在本文研究的范围内数值模拟与试验结果吻合较好，故采用上述数值模拟方法分析了翅片间距和开缝高度对双向开缝翅片管换热器传热与阻力特性的影响规律。

2.1 翅片间距f对双向开缝翅片管换热器传热与阻力特性的影响

通过数值模拟，获得了如图7所示的翅片间距对双向开缝翅片管换热器传热与阻力特性的影响规律。其中，试件编号f=2.3、f=3.3、f=4.3表示翅片间距分别为2.3、3.3、4.3 mm，其余结构参数均相同（表1），且模拟工况也相同。

由图7(a)中可以看出，翅片间距对双向开缝翅片管换热器传热特性的影响与有关。当<7200时，空气侧随着翅片间距的增大而增大，这是因为f=2.3的翅片间距较小，上下边界层将会重合，传热形式主要为流体的导热，传热效果大大降低，即使有开缝的交错存在，对流体边界层有一定的破坏作用，但因为气流流通通道过于狭小，流体不能充分冲刷翅片表面进行对流换热，故f=2.3的空气侧较小；而随着翅片间距的增大，这一问题得到了有效解决；不过，对于整个换热器而言，在外形尺寸一定的情况下，翅片间距增大，尽管传热系数得到了提高，但因翅片数量的减少，空气侧总的换热面积也随之减少，两者综合影响可能会导致总换热量的减小。当>7200时，f=2.3的空气侧超过了f=3.3和f=4.3的空气侧，该规律与文献[20]获得的翅片间距对开缝翅片管换热器的传热特性的影响规律相似；随着的增大，旋涡流动成为主要流动方式，而翅片间距为2.3 mm、开缝高度为1.92 mm时，开缝桥面交错分布在相邻两翅片之间，相比于翅片间距为3.3、4.3 mm时，开缝导致的气流扰动更为剧烈，对翅片表面的冲刷更为全面，同时对边界层的破坏更为严重。

由图7(b)中可以看出，在同一下，空气侧随着翅片间距的增大而减小，即空气侧流动阻力随之减小，这是因为，在同一下，翅片间距越小，流通截面越小，扰动增强，因而使得空气侧流动阻力增大。

2.2 开缝高度h对双向开缝翅片管换热器传热与阻力特性的影响

开缝高度对双向开缝翅片管换热器传热与阻力特性的影响如图8所示。其中，试件编号h=1.60、h=1.92、h=2.24表示开缝高度分别为1.60、1.92、2.24 mm，其余结构参数均相同（表1），且模拟工况也相同。

由图8(a)可以看出，随着的增大，不同开缝高度的翅片管换热器空气侧均随之增大；在同一下，随着翅片开缝高度的增加，空气侧先减小后增大，这是因为，h=1.92的上、下翅片的开缝桥面处于同一平面上，而相对于h=1.92，开缝高度的升高或降低，都会导致相邻两桥面分开布置（图9），翅片间的扰动会变得更为剧烈，热边界层的破坏程度也更为严重；又因为管束的热边界层是沿着翅片表面发展的，h=2.24的开缝与其相邻翅片距离更近，而h=1.60的开缝桥面与其本身的翅片距离较近，两者都有效减薄了翅片表面的热边界层厚度；越大，流体的扰动越剧烈，会形成复杂的流体旋涡流动，而开缝高度的增加，使得这一现象更为明显，从而有效地强化了空气侧对流换热。

由图8(b)可以看出，在同一下，随着开缝高度的增大，空气侧先减小后增大，即空气侧流动阻力先减小后增大。这是因为h=2.24的相邻两桥面互相交错，h=1.60的相邻两桥面互相分离，两者均减小了气流在翅片间的流通面积，增加了流体的扰动，从而增加了阻力；而h=2.24的流通截面最小，故其阻力最大。

2.3 翅片结构对换热器综合流动传热性能的影响

为了比较双向开缝翅片管换热器的综合流动传热性能，本文采用性能评价指标·-1/3对不同翅片结构的换热器进行性能分析。·-1/3的值反映了流体在流经传热表面时，单位功耗的对流换热的强弱。对于所研究的单个翅片单元，·-1/3的值越大，说明管束的综合流动传热性能越优[10]。

根据数值模拟结果，=2734～6712范围内，5种翅片结构的换热器的综合流动传热性能的评价准则·-1/3如图10所示。从图中可以看出，随着的增大，评价准则·-1/3增大，即翅片管束综合流动传热性能提高，这是因为随着的增大而增大，随着的增大而减小；在同一下，改变翅片开缝高度，其综合流动传热性能相近，因此，在实际工程应用时，可根据实际情况选择不同的开缝高度，如要求传热性能较好，可考虑采用h=2.24开缝翅片管换热器，如要求阻力尽可能小，则可以选择h=1.92开缝翅片管换热器；f=4.3的综合流动传热性能最佳，主要是因为和较小翅片间距的翅片管束相比，尽管其传热性能提高不明显，但其阻力明显减小了，不过在换热器外形尺寸一定时，翅片间距的增大会使翅片数减少，换热面积减小，反而会降低双向开缝翅片管换热器的换热能力，因此f=4.3单个翅片单元的换热器综合流动传热性能最优，但对于外形尺寸相同的双向开缝翅片管换热器而言其传热性能不一定最好。在本研究中，在一定范围内，存在最优翅片间距，需综合考虑。

3 结 论

采用数值模拟与模化试验相结合的方法研究了开缝结构对双向开缝翅片管换热器传热与阻力特性的影响规律，得出以下结论。

（1）空气侧的变化对双向开缝翅片管换热器的传热与阻力性能有显著影响。由于热阻主要集中在空气侧，所以增大空气流速可显著提高双向开缝翅片管换热器的传热性能，同时，空气侧流动阻力也会逐渐增加。

（2）翅片间距在2.3～4.3 mm范围内，当<7200时，空气侧随着翅片间距的增大而增大，而当>7200时，f=2.3的空气侧超过了f=3.3和f=4.3的空气侧；空气侧流动阻力随着翅片间距的增大而减小。对换热器一个翅片单元空间而言，f=4.3的综合流动传热性能最佳，但是当换热器外形尺寸一定时，由于换热面积的减小，其换热量可能减小，所以需要结合实际情况综合考虑。

（3）开缝高度在1.60～2.24 mm范围内，随着翅片开缝高度的增大，空气侧和流动阻力均先减小后增大；3个开缝高度翅片的换热器综合流动传热性能相近，此时应视具体情况选择翅片结构，如需换热性能好，可选择h=1.60或h=2.24，如要求阻力小，可选择h=1.92。

（4）本文的数值模拟方法有一定的准确性，可用于拓展研究其他因素对双向开缝翅片管换热器传热与阻力特性的影响规律。

符 号 说 明

do——翅片管基管外径，mm Eu——Euler数 f——范宁摩擦因子 Nu——Nusselt数 Pf——翅片间距，mm Re——Reynolds数 Sh——开缝高度，mm Sw——开缝宽度，mm S1——管束横向间距，mm S2——管束纵向间距，mm δ——翅片管基管壁厚，mm δf——翅片厚度，mm

References

[1] 刘忠民, 鹿红伟, 郑学利. 空调用翅片新技术的数值模拟研究与应用[J]. 制冷, 2011, 30(3): 6-12. LIU Z M, LU H W, ZHENG X L. Numerical simulation and application of new technology for air conditioner fin [J]. Refrigeration, 2011, 30(3): 6-12.

[2] 李军, 吴学红, 徐青, 等. 波纹开缝翅片管换热器传热与流动性的数值模拟[J]. 广东海洋大学学报, 2008, 28(4): 82-85. LI J, WU X H, XU Q,. Numerical simulation of heat transfer and flow performance of slit surfaces of wave plate for fin and tube heat exchangers [J]. Journal of Guangdong Ocean University, 2008, 28(4): 82-85.

[3] 钱力, 吴学红, 吕彦力. X型开缝翅片传热与流动性能的数值模拟[J]. 郑州轻工业学院学报（自然科学版）, 2011, 26(4): 45-49. QIAN L, WU X H, LÜ Y L. Numerical simulation of heat transfer and fluid flow characteristics of X-shaped slit of fin [J]. Journal of Zhengzhou University of Light Industry (Natural Science), 2011, 26(4): 45-49.

[4] 李慧珍, 屈治国, 程永攀, 等. 开缝翅片流动和传热性能的实验研究及数值模拟[J]. 西安交通大学学报, 2005, 39(3): 229-232. LI H Z, QU Z G, CHENG Y P,. Experimental and numerical study on heat transfer and fluid flow characteristics of slotted fin-and-tube heat transfer surfaces [J]. Journal of Xi’an Jiaotong University, 2005, 39(3): 229-232.

[5] DU Y J, WANG C C. An experimental study of the airside performance of the super slit fin-and-tube heat exchangers [J]. International Journal of Heat and Mass Transfer, 2000, 43(24): 4475-4482.

[6] YUN J Y, LEE K S. Influence of design parameters on the heat transfer and flow friction characteristics of the heat exchanger with slit fins [J]. Heat and Mass Transfer, 2000, 43(14): 2529-2539.

[7] TANG L H, ZENG M, WANG Q W. Experimental and numerical investigation on air-side performance of fin-and-tube heat exchangers with various fin patterns [J]. Experimental Thermal and Fluid Science, 2009, 33(5): 818-827.

[8] 尹斌, 丁国良, 欧阳惕. 开缝型翅片流动与传热三维数值模拟[J]. 热科学与技术, 2007, 6(2): 141-145. YIN B, DING G L, OUYANG T. Three-dimensional numerical simulation of flow and heat transfer on slit fins [J]. Journal of Thermal Science and Technology, 2007,6(2): 141-145.

[9] 鹿钦礼, 熊新强, 马贵阳, 等. 开缝翅片换热器三维流动传热特性数值研究[J]. 当代化工, 2010, 39(6): 706-708. LU Q L, XIONG X Q, MA G Y,. Numerical study on three-dimensional flow heat transfer characteristics of the slot fin heat exchanger [J]. Contemporary Chemical Industry, 2010, 39(6): 706-708.

[10] 杨立军, 贾思宁, 卜永东, 等. 电站间冷系统空冷散热器翅片管束流动传热性能的数值研究[J]. 中国电机工程学报, 2012, 32(32): 50-57. YANG L J, JIA S N, BU Y D,. Numerical study on flow and heat transfer characteristics of finned tube bundles for air-cooled heat exchangers of indirect dry cooling systems in power plants [J]. Proceedings of the CSEE, 2012, 32(32): 50-57.

[11] 袁益超, 廖飞页, 赵存江, 等. 双向开缝翅片管换热器传热与阻力特性试验研究[J]. 热科学与技术, 2014, 13(3): 235-239. YUAN Y C, LIAO F Y, ZHAO C J,. Experimental study on heat transfer and resistance characteristics of superslit finned tube exchanger [J]. Journal of Thermal Science and Technology, 2014, 13(3): 235-239.

[12] 赵存江, 袁益超, 廖飞页, 等. 单向开缝翅片管换热器传热与阻力性能的数值模拟及试验研究[J]. 能源工程, 2014, (5): 9-13. ZHAO C J, YUAN Y C, LIAO F Y,. Numerical simulation and experimental study on heat transfer and resistance characteristics of unidirectional slotted fined and tube exchanger [J]. Energy Engineering, 2014, (5): 9-14.

[13] 衣志超, 袁益超, 王学刚. 管间距对开缝翅片管换热器传热与阻力特性的影响[J]. 能源工程, 2015, (5): 9-14. YI Z C, YUAN Y C, WANG X G. Influences of tube pitch on heat transfer and resistance characteristics of the slotted fin and tube heat exchanger [J]. Energy Engineering, 2015, (5): 9-14.

[14] 曾小林, 林金国, 童小川. 翅片间距对翅片管换热性能影响分析[J]. 机电设备, 2015, (1): 65-69. ZENG X L, LIN J G, TONG X C. Research on the influence of fin spacing to the heat transfer performance of finned tube [J]. Mechanical and Electrical Equipment, 2015, (1): 65-69.

[15] 于新娜, 袁益超, 马有福, 等. H形翅片管束传热和阻力特性的试验与数值模拟[J]. 动力工程学报, 2010, 30(6): 433-438. YU X N, YUAN Y C, MA Y F,. Experimental tests and numerical simulation on heat transfer and resistance characteristics of H-type finned tube banks [J]. Power Engineering, 2010, 30(6): 433-438.

[16] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006. YANG S M, TAO W Q. Heat Transfer [M].4th ed. Beijing: Higher Education Press, 2006.

[17] 陶文铨. 数值传热学[M]. 西安: 西安交通大学出版社, 2001. TAO W Q. Numerical Heat Transfer [M]. Xi’an: Xi’an Jiaotong University Press, 2001.

[18] LEMIUEDDA A, SCHMID A, FRANZ E,. Numerical investigations for the optimization of serrated finned-tube heat exchangers [J]. Applied Thermal Engineering, 2011, 31: 1393-1401.

[19] 叶大钧. 热力机械测试技术[M]. 北京: 机械工业出版社, 2000. YE D J. Test Technologies of Thermodynamic Mechanism [M]. Beijing: Mechanical Industry Press, 2000.

[20] WANG C C, LEE W S, SHEU W J. A comparative study of compact enhanced fin-and-tube heat exchangers [J]. International Journal of Heat Mass Transfer, 2001, 44(18): 3565-3573.

Effects of fin structure on heat transfer and resistance characteristics of super slit finned tube heat exchangers

TU Qilang, YUAN Yichao, HU Xiaohong

(Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

To understand the effect of fin structure on heat transfer and resistance, numerical simulation and validation experiments were performed on super slit finned tube heat exchangers with different fin pitchesfand slit heightsh. Whenwas less than 7200, heat transfer and resistance performance was improved withfincrease. Whenwas greater than 7200, heat transfer was improved but resistance was declined withfdecrease. In case ofhincrease, heat transfer declined first and enhanced later, whereas resistance showed an opposite trend. With regard to five super slit finned tube heat exchangers with different fin structures, the comprehensive flow and heat transfer performance were improved while the actual heat transfer area was decreased withfincrease, which a consideration of all factors should be required. A good agreement was observed between the numerical simulation and experimental results whenwas in the range of 2734—6712, indicating that the numerical simulation method could predict the heat transfer and resistance characteristics of super slit finned tube heat exchangers. These results would set a basis for optimization between structure and performance of these heat exchangers.

super slit finned tube heat exchangers; heat transfer; numerical simulation; modeling experiment; comprehensive flow and heat transfer performance; optimization

2016-05-31.

10.11949/j.issn.0438-1157.20160756

TK 223

A

0438—1157（2016）11—4615—08

屠琦琅（1992—），男，硕士研究生。

2016-05-31收到初稿，2016-07-08收到修改稿。

联系人：袁益超。

Prof. YUAN Yichao, ychyuan@163.com