基于Modelica的永磁同步电机系统建模及控制参数优化*

马小辉，李志华，刘婷婷

（杭州电子科技大学机械工程学院，浙江 杭州 310018）

基于Modelica的永磁同步电机系统建模及控制参数优化*

马小辉，李志华，刘婷婷

（杭州电子科技大学机械工程学院，浙江 杭州 310018）

永磁同步电机系统是一个涉及机、电、磁、控等多个领域的系统，针对其多领域耦合、非线性和时变特性，提出一种基于Modelica语言和响应面的系统建模及控制参数优化方法。首先基于多领域统一建模理论、在MWorks平台上建立了永磁同步电机系统的多领域统一模型，包括：永磁同步电机子模型、矢量控制子模型、负载子模型和电压逆变器子模型；然后利用拉丁超立方（LHS）采样方法，构建了永磁同步电机系统转速超调量与PID控制参数之间的响应面模型；最后，基于响应面模型，对PID控制参数进行了整定优化。仿真结果表明经过整定优化后的控制参数能够使电机快速准确地跟踪转速指令，同时电机输出扭矩能够及时响应负载的要求，电机控制精度高、响应速度快。

永磁同步电机；控制参数优化；Modelica；响应面法

永磁同步电机具有体积小、效率高、功率因数高等特点，在数控机床、机器人、航空航天器等方面得到广泛应用［1］。永磁同步电机系统是典型的集机、电、磁、控等多领域于一体的复杂机电系统，目前工程上对控制参数的整定一般是依靠经验在实物系统上进行调节。

为了更好地控制永磁同步电机，Lin［2］将神经网络控制与PID控制相结合；Errouissi等人［3］采用一个非线性的预测控制器，以增强闭环系统的稳定性。在PID控制参数整定方面，Underwood［4］等人提出了在线参数估计法；丁建完等人［5］采用蒙特卡洛随机试验方式整定PID参数；彭安华等人［6］采用正交试验法整定PID参数。这些方法在实际应用时往往是繁琐、困难的。

由于永磁同步电机系统存在着复杂的机－电－磁－控等多领域耦合问题，如果采用不同领域工具，对其分属于不同领域的各个部分进行分别建模，然后集成，则势必会因系统耦合性差、集成度不高而造成仿真精度和效率等方面的问题。如果采用多领域统一建模的方法，就能够在一个系统化的理论基础上采用统一的工具平台，对永磁同步电机系统进行统一建模和仿真分析，从而克服采用工具集成的方法所带来的问题。

本文基于Modelica语言、在MWorks平台上建立了永磁同步电机系统的多领域统一模型，分析了不同负载下转速超调量的变化规律，构建了转速超调量与PID控制参数之间的响应面模型，实现了控制参数的整定优化，对于实际工程中的参数整定具有一定的指导意义和应用价值。

1 模型构建

1.1永磁同步电机模型

为了实现永磁同步电机转矩线性化控制，需要对转矩的控制参数进行解耦。假设磁路不饱和、空间磁场呈正弦分布、不计磁滞和涡流损耗影响［7］，以转子结构凸装式的永磁同步电机为对象，其定子ABC 坐标系、oaβ坐标系与转子odq坐标系的关系如图1所示。

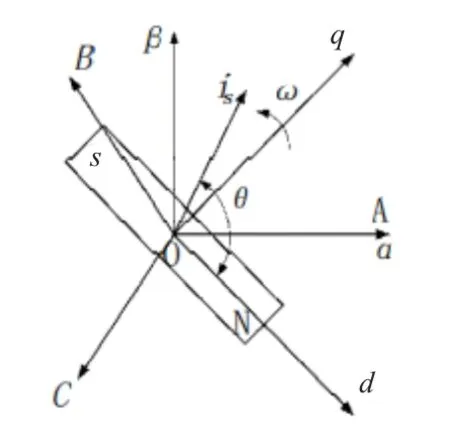
图1　定子ABC 坐标系、oaβ坐标系与转子odq坐标系的关系

oaβ坐标系为定子静止坐标系，a轴与定子绕组A相轴重合；odq为转子旋转坐标系，d轴与转子的磁链方向重合，并以相同转速ω逆时针旋转。将定子电流矢量is在dq轴上进行分解：is=id+iq，这样，经矢量变换后，永磁同步电机系统在与转子同步旋转的dq轴系下就可实现电流的解耦。其数学模型可以表达如下：

电机输出扭矩为：TE=1.5p［dφfiq+（Ld－Lq）］idiq采用id=0的、控制iq转子磁场的定向方法可以简单地实现最大转矩控制，故有：Te=1.5pdφfiq。

其中：Ud、Uq、id、iq、 φdd、 φdq、Ld、Lq、Lmd、Lmq分别表示永磁同步电机d轴、q轴方向的电压、电流、磁链、电感、主电感， φdf表示永磁体的转子磁链，p表示电机磁极对数，V0表示电机额定转速下的开路相电压，fnominal、Rs、lssigma分别fnominal表示永磁同步电机额定频率、定子电阻、漏电感，Tm表示外加负载扭矩，Jr表示电机自身转动惯量，Br表示电机的粘性摩擦系数，ωr表示电机转速。

根据以上分析，得到永磁同步电机Modelica模型如图2所示。

1.2矢量控制模型

矢量控制是一种高性能交流电机控制方式，矢量控制变频调速的做法是将异步电动机在三相坐标系下的定子电流通过三相/二相变换，等效成两相静止坐标系下的交流电流，再通过转子磁场定向旋转变换，等效成同步旋转坐标系下的直流电流，然后模仿直流电动机的控制方法，求得直流电动机的控制量，然后经过相应的坐标反变换，实现对异步电动机的控制［8］。

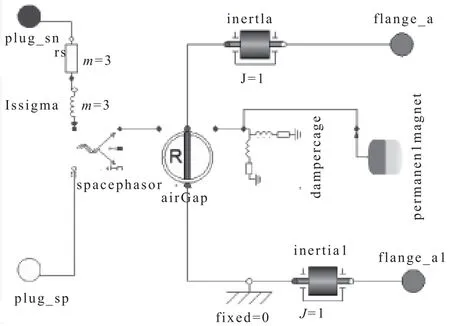
图2　永磁同步电机Modelica模型

为提高系统的鲁棒性和响应的快速性，采用速度环、电流环双闭环的控制方案，各环节均采用PID调节器，通过控制q轴方向电流，实现对永磁同步电机的矢量控制［9］。系统的性能主要由速度环决定，速度环可以增强系统的抗负载扰动能力，而电流环的作用只是及时抑制电流环的内部干扰［10］。矢量控制Modelica模型如图3所示。

图3　矢量控制Modelica模型

1.3负载模型

本文主要研究电机启动时，PID控制器的三个控制参数与转速超调量之间的关系。电机启动时负载为固定值或为零，其Modelica模型如图4所示。

1.4电压逆变器模型

电压逆变器模型是实现直流电（DC）转化为交流电（AC）的目的，其输入为矢量控制模块给出的控制信号，输出为三相电压脉冲波。根据逆变器物理电路结构搭建的Modelica模型如图5所示。

图4　负载Modelica模型

图5　电压逆变器Modelica模型

1.5整体模型

采用速度、电流双环控制方式，在MWorks平台上将各个子模型连接成系统的整体模型，它包括永磁同步电机子模型、矢量控制子模型、负载子模型和电压逆变器子模型，如图6所示。

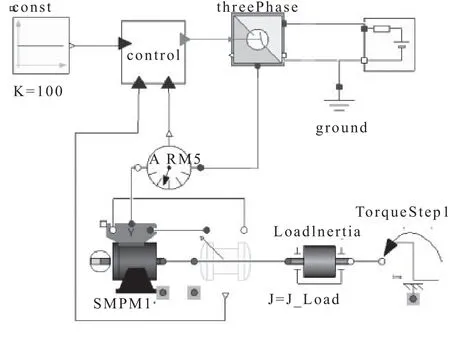
图6　永磁同步电机系统Modelica模型

响应面方法是用有限的实验来回归拟合一个关系，将其表示成显示函数，并以此来代替系统真实的

2 响应面方法

2.1响应面模型曲面。设第j次实验的响应值yj与实验因素xh（h=1，2，…，m；h为实验因素的个数；m为实验因素的总数）间的函数关系为yj=f（x1，x2，...，xm）+εj，εj为拟合误差，服从均值为零、方差为σ22的正态分布N（0，σ22）。常见的响应面模型有一阶响应面模型：

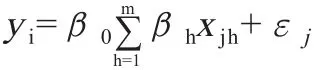
二次响应面模型：

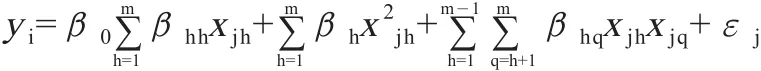
其中，β0表示常数项，βh表示实验因素xh的线性效应，βhh表示xh的二次效应，βhq表示两个不同实验因素xh和xq之间的交互效应，xjh、xjq表示第j次实验因素xh、xq的取值。对于含有n个变量的系统，构建一阶响应面模型至少需要做（n+1）次独立的仿真实验，构建二次响应面模型至少需要做次独立的仿真实验。

2.2拟合度评价指标

响应面模型对实验数据的拟合程度，常用的评价指标之一是均方根误差：

3 实验设计及参数整定

永磁同步电机系统的PID控制参数有比例参数Kp、积分参数Ti和微分参数Td。确定控制参数取值范围的方法如下：在临界振荡法［6］整定的基础上，先保持其他控制参数不变，单独改变某一控制参数的取值，使其由零逐渐增大，研究阶跃响应超调量和上升时间的变化情况，从而得到控制参数的取值范围为：Kp∈［0.1，10］、Ti∈［0.1，10］、Td∈［0.001，0.1］。

在电机结构参数固定的情况下（如表1所示），启动时的转速超调量y是与控制参数Kp、Ti、Td相关的隐式函数。本文采用响应面的方法构建近似函数，使用多种二次响应面模型构建永磁同步电机系统启动时的转速超调量响应函数，并根据其拟合程度选择最合适的响应面。

首先，在Matlab中采用拉丁超立方（LHS）采样，得到十组控制参数值。然后给定电机转速指令100 rad/s，无负载情况。最后，基于前面建立的永磁同步电机系统Modelica模型，在MWorks中进行仿真，得到系统启动时的转速超调量y值，如表2所示。

表1　永磁同步电机结构参数

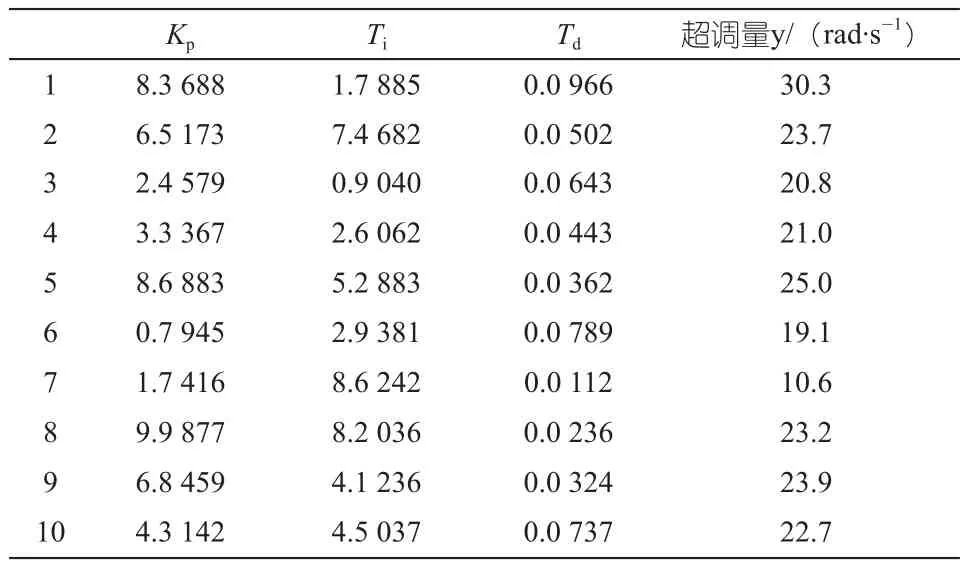
表2　采样及仿真结果

利用表2中的样本，可以得到转速超调量y与控制参数Kp、Ti、Td的完整二次响应面函数和不含平方项的非完整二次响应面函数。前者的均方根误差RMSE=5.173 3，后者的均方根误差RMSE=0.08 855，RMSE值越小说明该响应面模型越准确，所以采用不含平方项的二次响应面函数：

y=0.075 2KpTi+3.611 5KpTd+10.940 1TiTd+0.8 631Kp－1.342 4Ti+12.276 5Td+17.794 3

在M a t l a b中优化求解上述响应面函数，得到最佳的控制参数值：Kp=0.310，Ti=10，Td=0.01，Kp=1.5，Ti=0.670，Td=0.005，此时理论超调量为5.1 rad/s，实际超调量为5.3 rad/s。

4 仿真分析

4.1不同转速指令下的仿真结果

给定转速指令为10 rad/s，无负载情况下，仿真得到电机转速响应曲线如图7所示。此时，电机启动时的转速超调量为3.5 rad/s，达到稳态的时间为0.025 s。

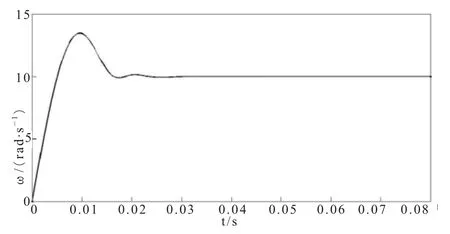
图7　电机转速响应曲线

给定转速指令为100 rad/s，无负载情况下，仿真得到电机转速响应曲线如图8所示。此时，电机启动时的转速超调量为5.3 rad/s，达到稳态的时间为0.023 s。

图8　电机转速响应曲线

给定转速指令为500 rad/s，无负载情况下，仿真得到电机转速响应曲线如图9所示。此时，电机启动时的转速超调量为6 rad/s，达到稳态的时间为0.025 s。

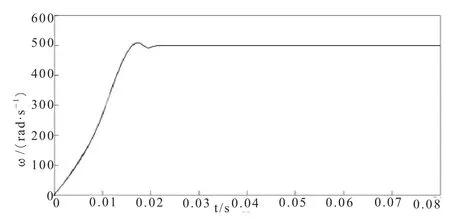
图9　电机转速响应曲线

从上述仿真结果（图7～图9）可以看出，经过响应面模型整定后的控制参数能够使电机快速准确地跟踪转速指令，其控制精度高、响应快。

4.2不同负载条件下的仿真结果

给定转速指令为100 rad/s，负载分别为2 N·m、4 N·m、6 N·m、8 N·m，仿真得到电机转速响应曲线如图10所示，电机输出扭矩响应曲线如图11所示。

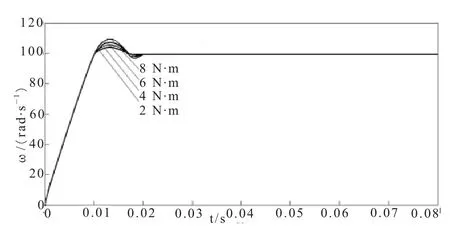
图10　不同负载条件下的电机转速响应曲线

从图10和图11可以看出，不同负载条件下，电机都能快速准确地跟踪转速指令，快速达到稳定状态，同时电机输出扭矩能快速准确地响应负载的要求。

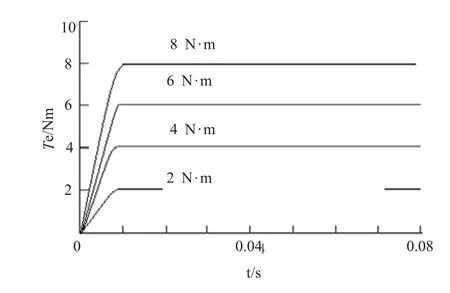
图11　不同负载条件下的电机输出扭矩响应曲线

5 结束语

永磁同步电机系统是一个典型的多领域耦合系统，本文基于Modelica语言、在MWorks平台上建立了永磁同步电机系统的多领域统一模型，该模型可用于系统的高置信度仿真。此外，由于电机启动时的转速超调量与PID控制参数之间的关系是一种隐式函数关系，因此本文采用二次响应面方法来构建其近似函数，然后基于该响应面函数，对PID控制参数进行了整定优化。仿真结果显示，经过整定优化后的控制参数能够适应不同的工况，其控制精度高、响应速度快。本文所提出的方法简单方便，具有一定的工程应用价值和借鉴作用。

［1］ Sui J， Wang J， Fan J， et al. Application and simulation of SVPWM in permanent-magnet synchronous motor s y s t e m［J］. O r d n a n c e I n d u s t r y A u t o m a t i c， 2 0 11，30（3）:55～58.

［2］ Lin C H. Hybrid recurrent wavelet neural network control of PMSM servo-drive system for electric scooter［J］. International Journal of Control， Automation and Systems，2014， 12（1）:177～187.

［3］ Errouissi R， Ouhrouche M， Chen W H， et al. Robust nonlinear predictive controller for permanent-magnet synchronous motors with an optimized cost function［J］. IEEE Transactions on Industrial Electronics， 2012，59（7）:2 849～2 858.

［4］ Underwood S J， Husain I. Online parameter estimation and adaptive control of permanent-magnet synchronous machines［J］. IEEE Transactions on Industrial Electronics，2010， 57（7）:2 435～2 443.

［5］ 丁建完.超低速PMSM系统的Modelica建模及控制参数整定［J］.电气传动，2013，43（4）:3～7.

［6］ 彭安华，孙旭东，王智明. 基于正交试验法的PID控制器参数整定［J］. 机械科学与技术， 2011，30（6）:1 028～1 032.

［7］ Li Z H， Yang H G， Yu J. Modeling and optimization of PMSM-precision reducer system with Modelica［J］. International Journal of Materials and Structural Integrity，2012， 6（2/3/4）:319～330.

［8］ Yu J P， Yu H S， Chen B， et al. Direct adaptive neural control of chaos in the permanent magnet synchronous motor［J］. Nonlinear Dynamics， 2012， 70（3）:1 879～1 887.

［9］ Li Y M， Tong S C， Li T S. Adaptive fuzzy output feedback control for a single-link flexible robot manipulator driven DC motor via back stepping［J］. Nonlinear Analysis-Real World Applications， 2013， 14（1）:483～494.

［10］ 李政，胡广大，崔家瑞，等. 永磁同步电机调速系统的积分型滑模变结构控制［J］. 中国电机工程学报，2 0 1 4，34（3）:431～437.

（P-01）

Modelica based PMSM system modeling and control parameter optimization

TH122；TP391

1009-797X（2016）10-0078-06

A

10.13520/j.cnki.rpte.2016.10.031

马小辉（1993-），男，硕士研究生，研究方向为多领域建模与仿真。

2016-04-13

国家自然科学基金资助项目（5 1 2 7 5 1 4 1，51305112）。