一种基于数据包含度的自动聚类算法
2016-11-18马云红王成汗江腾蛟张堃
马云红, 王成汗, 江腾蛟, 张堃
(西北工业大学 电子信息学院, 陕西 西安 710072)
一种基于数据包含度的自动聚类算法
马云红, 王成汗, 江腾蛟, 张堃
(西北工业大学 电子信息学院, 陕西 西安 710072)
聚类分析是机器学习和模式识别领域的一个重要问题,聚类算法常用于解决这类问题。针对传统聚类算法运算量大、不适应任意分布数据聚类的不足,提出了一种基于数据包含度的自动聚类算法。该算法引入数据包含度的概念,能够自动确定聚类个数和聚类中心,并进一步采用跟随策略实现聚类。多组数据的实验验证了自动聚类算法的有效性。对不同分布的数据进行了自动聚类算法与K-means聚类算法的聚类结果比较,实验结果表明自动聚类算法具有很好的聚类性能。
聚类算法;数据包含度;数据局部密度
聚类分析是机器学习和模式识别领域的一个非常活跃又极具挑战性的研究方向。它是根据数据样本间的相似性将样本划分到不同的类簇,使同类簇中数据样本之间相似度高,异类簇中数据样本之间相似度低。典型的算法有K-means聚类算法[1]、谱聚类算法[2]、DBSCAN算法[3]以及CFSFDP算法[4]等。K-means聚类算法是找出K个聚类中心,按照最邻近原则将数据集合中的数据划分到K个聚类中,然后根据判定函数调整数据归属。谱聚类算法的思想以图论、相似性为基础,将聚类问题转化为无向图的多路划分问题。谱聚类算法计算较耗时。DBSCAN算法是基于密度的聚类算法,算法可以进行任意数据分布的聚类。Alex Rodriguez和Alessandro Laio提出一种CFSFDP算法[4],基于密度峰值和距离的计算,将数据点自身的密度较大且相互距离较远的数据点作为聚类中心点。该算法能够识别任意分布的聚类簇,并且计算简单快速,但需要人工介入对聚类个数进行确定。本文在CFSFDP算法的基础上,提出一种基于数据包含度的自动聚类算法ACA(automatic clustering algorithm)。该算法通过计算数据点的综合考虑量,并据此降序排序。对排序后的数据序列依次计算数据包含度。根据数据包含度的值自动确定聚类个数,同时确定聚类中心,最后结合跟随策略实现自动聚类。
1 相关定义
定义1 截断距离dc,一个距离阈值,用于计算每个数据点的局部密度。
定义2 局部密度ρi,表示数据点集中与xi的距离小于截断距离dc的其他数据点个数。
对于包含N个数据点的数据点集合S,集合S中数据点xi的局部密度ρi定义为S中与xi的距离小于截断距离dc的其他数据点的个数,表示为(1)式:式中dij是数据点xj和xi间的欧氏距离;χ(dij-dc)函数用以判断xj距xi是否小于距离阈值dc,表达式如(2)式所示。根据定义,可以计算出数据集中每个点的局部密度。
(1)
(2)
定义3 距离δi表示数据点xi到比它局部密度高的其他数据点的最小距离。定义为(3)式。
(3)
定义4 综合考虑量γi,表示每个数据点的局部密度与距离的乘积。局部密度大说明聚在这个点周围的数据点多;距离大说明该点距离其他潜在中心的距离远。综合考虑量越大,则越容易成为聚类中心。
对于N个数据点集合S中第i个数据点的综合考虑量γi由(4)式计算。
(4)
定义5 数据包含度μl,表示聚类后对数据点集合中的数据点的包含程度。
对于N个数据点集合S。根据每个数据点的综合考虑量值进行降序排序。综合考虑量大的数据点更容易成为聚类中心。假设数据集合可以聚类成M个类,则必然是综合考虑量排在前M个的数据点为聚类中心,如何确定聚类个数M,需要根据数据包含度来计算。数据包含度的计算公式如(5)式所示
(5)
2 自动聚类算法原理
2.1 聚类个数的自动确定
自动聚类算法可以自动确定聚类个数M并确定聚类中心。它是根据数据包含度μl的值确定的。如果μl=1,则说明聚类包含了所有的数据点。如果 μl>1,则说明包含的数据点数量大于原始数据的数量,也就意味着有部分数据被重复分类到不同的类中。如果 μl<1,则说明有部分数据没有被分到聚类中。根据综合考虑量的排序,从综合考虑量最大的点开始,依次计算以这些点作为聚类中心时的数据包含度,直到发现 μl=1,此时的l值作为聚类个数M,对应的M个点即为聚类中心点。若不能满足 μl=1,则寻找满足 μl>1且 μl-1<1的l,取l-1为聚类个数。
2.2 基于跟随策略实现非聚类中心数据点划分
基于数据包含度的计算,确定了聚类个数,并同时确定了聚类中心点,余下的工作就是将非聚类中心点的其他数据点划分到聚类中。论文采用跟随策略进行非聚类中心数据点的划分。
跟随策略:对于非聚类中心的样本数据i(i≥M+1),将点i划分到比自身综合考虑量大且距离自身最近的样本点所属的类簇。假设已经确定的聚类个数为M,则前M个点为聚类中心,将第M+1个数据根据距离最近原则划分到前M个聚类中心的一个类中;同理,将数据集合中第j(M+1
3 自动聚类算法实现过程
对于包含N个数据点的集合S,聚类步骤为:
1) 初始化截断距离参数dc。
2) 根据截断距离参数dc计算集合S中每个数据点的局部密度ρi。
3) 对集合S中数据点按局部密度ρi的值进行降序排序得S′={xβ1,xβ2,…,xβN},βi记录数据点的原始编号。
4) 根据(3)式顺序计算集合S′中下标为βi的数据点的距离δβi。
5) 依次计算数据点集合S′中下标为βi的数据点的综合考虑量γβi。

7) 顺次计算数据包含度μl,(l=1,2…),并根据μl的值确定聚类个数,进而确定聚类中心。
8) 采用跟随策略对非聚类中心的其他数据点进行聚类划分。
4 实验验证分析
为了验证本文提出的自动聚类算法性能,本文采用Aggregation数据、Flame数据和Spiral数据作为测试样本集,进行聚类算法验证,并与经典的K-means聚类算法进行了比较。
4.1 自动聚类算法验证
以Aggregation数据进行聚类个数确定的验证。图1为Aggregation数据分布图。它含有788个数据点,数据点为二维无量纲数值。从直观分析,数据应分为7个聚类。实验中,自动聚类算法计算出的数据包含度曲线如图2所示。从图2中可以看出,满足μl>1且μl-1<1的l为8,则聚类个数选l-1为7。自动聚类个数选取正确。
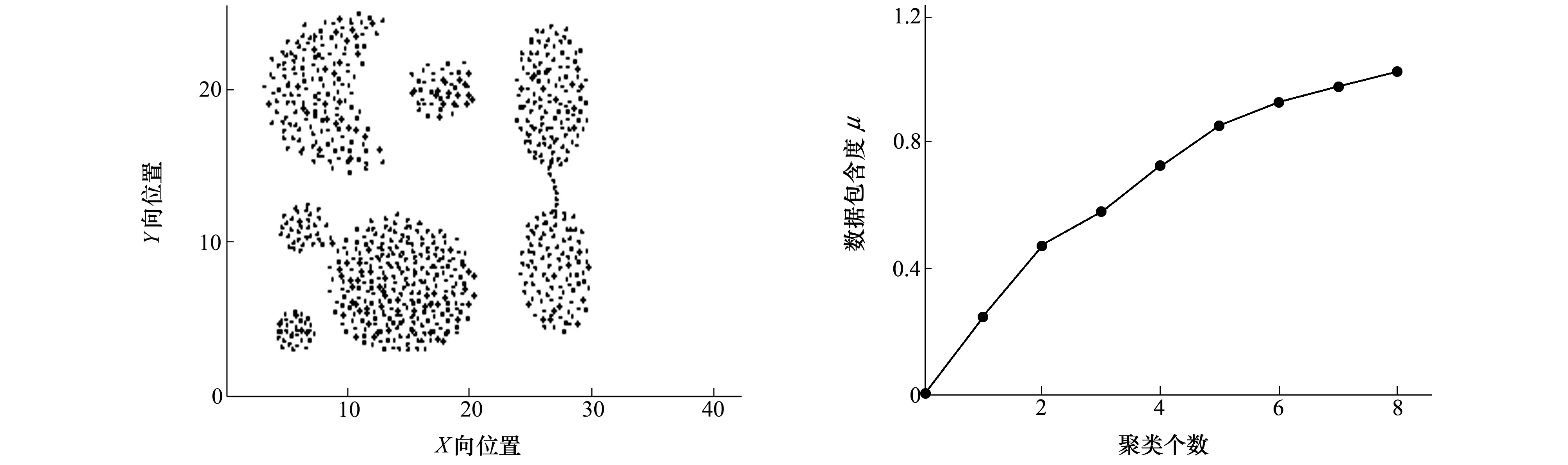
图1 Aggregation数据的分布 图2 Aggregation数据的数据包含度
4.2 自动聚类(ACA)算法与K-means算法比较
为了验证自动聚类算法的广泛有效,本文进行了大量的标准数据验证,并与传统聚类算法进行了比较分析。图3是ACA算法对Flame数据的聚类结果,将Flame分成了焰心和外焰两部分。图4是K-means算法对Flame数据的聚类结果,将部分外焰数据误分到了焰心部分。图5是ACA算法对Spiral数据的聚类结果,图中正确分出了3个螺旋线。图6是K-means算法对Spiral数据的聚类结果,将螺旋线数据分成了三等分扇形空间,没有分出螺旋线。从分类结果图中可以看出,自动聚类算法对实验数据的聚类效果比较理想,而K-means聚类算法的分类结果不合理。表1列出了2种算法对于2组数据误分率的数值比较。实验数据说明K-means聚类算法具有一定的局限性,自动聚类算法的聚类结果理想。
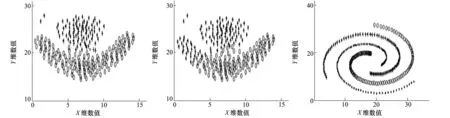
图3 ACA算法进行Flame数据聚类 图4 K-Means算法进行Flame数据聚类 图5 ACA算法进行Spiral数据聚类
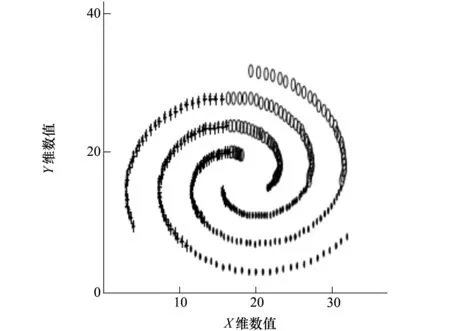
图6 K-Means算法进行Spiral数据聚类
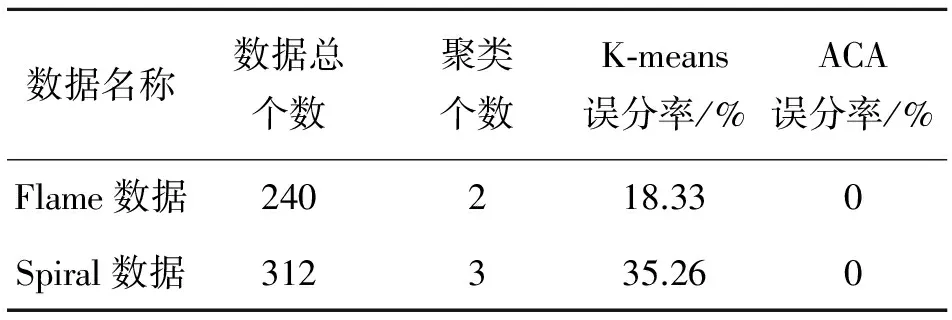
数据名称数据总个数聚类个数K⁃means误分率/%ACA误分率/%Flame数据240218.330Spiral数据312335.260
5 结 论
本文提出了一种基于数据包含度的自动聚类算法。该算法基于数据包含度的计算实现了自动确定聚类个数和聚类中心点,并进一步采用跟随策略实现数据点集合聚类。自动聚类算法的实现过程简单,不需迭代和考虑收敛,计算量小,计算速度快。大量数据样例的聚类实验证明自动聚类算法有效可靠。与经典K-means的仿真比较结果也证明了自动聚类算法能够理想地聚类,具有很好的适应性和鲁棒性。
[1] Zhang Z, Zhang J, Xue H. Improved K-Means Clustering Algorithm[C]∥Image and Signal Processing CISP′08 Congress on IEEE, 2008, 5: 169-172
[2] Wu J, Cui Z M, Shi Y J, Gong S R. Local Density-Based Similarity Matrix Construction for Spectral Clustering[J]. Journal of China Institute of Communications, 2013, 34(3): 14-22
[3] 冯少荣, 肖文俊. DBSCAN聚类算法的研究与改进[J]. 中国矿业大学学报,2008, 37(1): 105-110
Feng Shaorong, Xiao Wenjun. An Improved DBSCAN Clustering Algorithm[J]. Journal China University of Mining and Technology, 2008, 37(1): 105-110 (in Chinese)
[4] Rodriguez A, Laio A. Clustering by Fast Search and Find of Density Peaks[J]. Science, 2014, 344(6191): 1492-1496
An Automatic Clustering Algorithm Based on Data Contained Ratio
Ma Yunhong, Wang Chenghan, Jiang Tengjiao, Zhang Kun
School of Electronics and Information, Northwestern Polytechnic University, Xi′an 710072, China
Cluster analysis is an important issue for machine learning and pattern recognition. Clustering algorithm is usually used in solving these problems. A novel automatic clustering algorithm is developed based on data contained ratio. In automatic clustering algorithm which is presented in this paper, the concept of data contained ratio is proposed, the cluster number can be determined automatically based on the data contained ratio, and the relative cluster centers are found similarly Several groups data are used to testify and demonstrate the validity and effectiveness of the cluster algorithm. In addition, the comparison between the traditional K-means cluster algorithm and automatic cluster algorithm is processed. The results demonstrate that the automatic cluster algorithm has high performance in clustering random distribution data set.
clustering algorithm; data contained ratio; data local density
2016-03-05
西北工业大学研究生创意创新种子基金(G2015KY0407)与国家自然科学基金青年基金项目(61401363)资助
马云红(1972—),女,西北工业大学副教授、博士,主要从事人工智能优化算法、飞行器任务规划和智能控制、复杂系统建模与仿真的研究。
TP311.5
A
1000-2758(2016)05-0863-04
