基于微分对策的水下主动防御拦截导引方法

程瑞锋, 刘卫东,2, 高立娥,2, 张建军

(1.西北工业大学 航海学院, 陕西 西安 710072; 2.西北工业大学 水下信息与控制重点实验室, 陕西 西安 710072)



基于微分对策的水下主动防御拦截导引方法

程瑞锋1, 刘卫东1,2, 高立娥1,2, 张建军1

(1.西北工业大学 航海学院, 陕西 西安 710072; 2.西北工业大学 水下信息与控制重点实验室, 陕西 西安 710072)

针对来袭水下目标机动方式的无法预知的问题,为实现精确拦截,以目标捕获条件为约束,设计了一种用于水下机动目标拦截的微分对策导引律。以微分博弈理论为基础,构造用于双边最优控制的二次型性能指标,利用伴随原理求解终端问题的方法导出具有状态反馈形式“零效脱靶量”,并以其为性能指标设计用于航向角控制的微分对策制导律。通过对机动目标的跟踪拦截表明:该制导律对目标机动方式具有较强的鲁棒性,与最优导引相比,对机动目标的拦截精度高,可满足水下拦截作战技术需求。

微分对策;制导律;拦截;脱靶量

随着水下智能武器系统识别和跟踪能力的增强,实施以“硬杀伤”为主的水下主动防御拦截成为当前海战防御的研究热点。由于水下拦截器与来袭目标均属水下兵器,基于现有水下兵器结构的制约,水下拦截器与来袭目标相比,在航速和机动性方面并不占优势,但所拦截的目标却具有速度快、尺寸小及机动性强的特点[1]。同时,在拦截对抗过程中,双方都属于独立控制,且目标机动策略一般无法预测,在未知目标机动信息情况下实施对来袭目标的最优拦截非常困难。

微分对策控制是最优控制与对策论的有效融合[2],在处理对抗问题上具有明显优势。目前,微分对策已广泛应用到导弹拦截决策方面,文献[3]研究了弹目对抗的线性二次微分对策导引律;文献[4]应用研究了临近空间导弹拦截大机动目标的微分对策拦截制导律;文献[5]研究了目标机动信息时延可知情形的导弹拦截微分对策制导律。上述研究结合微分对策理论,提出了双方动态控制的微分对策制导律,通过有效控制使视线角速度趋于零,达到了优化拦截控制系统性能的目的。然而,由于水下拦截器的自导装置与壳体固连,且受水声物理场的制约,其探测范围和精度受到一定限制,同时由于声自导的波束较宽,往往在10°左右,加上水声传播信息量少,对目标的测量仅有距离或方位,难以利用目标所在波束的变化及拦截器航向角来推算视线转动速率[6],所以在水下防御拦截中直接应用现有的拦截微分对策制导律应用受到很大限制。本文充分考虑复杂水文条件对水下拦截器自导系统的影响,在已知来袭目标方位和距离或仅知目标方位信息实施的有利提前角角发射基础上,以拦截器捕获来袭目标条件为约束条件,提出了一种基于微分对策的主动防御拦截导引方法,使水下拦截器通过实时“零效”跟踪,实现对来袭目标的有效拦截。

1 问题描述

在海战中,我方舰潜接到来袭报警时,一般只能探测来袭目标所在方位和大致距离,为争取时间,尽快发射拦截器进行反击,在未知来袭目标航行方向和航速以及准确距离条件下,根据图1所示的拦截器对抗来袭目标阵位关系确定拦截器的发射角范围。

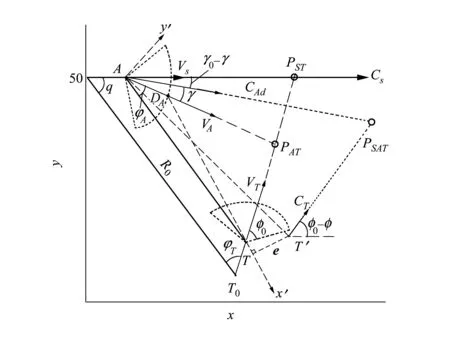
图1 拦截器对抗来袭目标阵位关系

(1)

由于多波束自导装置在水中兵器上的应用及自导作用距离的存在,当我方按正常提前角向相遇点AT发射拦截器时,只有当拦截器的自导扇面的前端中点DA与来袭目标构成相遇三角形TDAPA时,捕获概率方为最高[7]。为实现快速精确导引,须将拦截器与来袭目标的“瞬时相遇点”始终捕获在自导装置中间波瓣内。假定自导拦截时,拦截器的侧滑角很小,即可将拦截器的纵轴近似为拦截器的速度矢量方向。在拦截导引末段,由于观测误差和目标机动的存在,来袭目标往往偏离所在自导捕获波瓣,此时,拦截器须通过实时调整航向角变化γ来获得对目标的最高捕获概率,从而确保拦截器的精确导引和有效拦截。

2 微分对策制导律的设计

在末制导导引拦截中,拦截器同样进入了来袭目标的可探测区域,此时来袭目标能够感知拦截意图,从而进行机动规避。由于双方均属于独立控制,为使拦截器实施对来袭目标的最佳捕获和有效拦截,根据图2制导原理图,结合微分博弈对策理论对上述拦截问题进行数学建模。

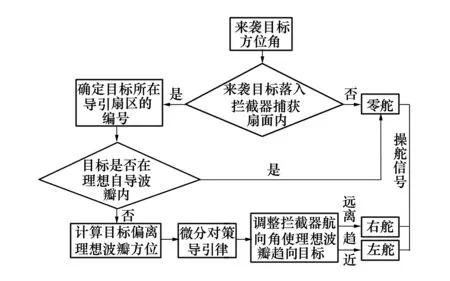
图2 基于微分对策制导拦截导引原理图

由图2可知,实施有效微分对策导引的首要条件是捕获目标。根据图1,当来袭目标机动到T′,航向角变化为φ时,在坐标系Ax′y′中,目标的实际瞄准与期望瞄准之间产生一定的偏差,有

yT-yA=e

(2)

式中，vR是Sx′方向的相对接近速度。拦截结束时间可由tf=R0/vR近似求得。此时,任一导引时间内来袭目标方位表示为

xTi=xT(i-1)+VTΔtcosφ0+esinq+vRΔtcosq

(3)

拦截器的瞬时方位为

(4)

拦截器捕获目标的条件表示为

(5)

式中，λ为拦截器自导扇面半角,r为拦截器的自导作用距离,γ0为拦截器初始航向角,γ为航向角变化量。以拦截器捕获目标为约束条件,取偏差e为变量x1,则有

(6)

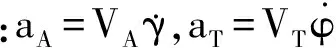
(7)

考虑工程应用性,假定拦截器具有延时时间常数为τA的一阶动态特性,来袭目标发现拦截后,实施固有频率为w的蛇形机动规避, 则有

(8)

(9)

式中

实际对抗中,作为主控方的水下拦截器所需的自身运动信息可通过自身传感器来获取,具有完全状态信息,而作为拦截方的来袭目标则具有被噪声干扰的观测信息。因此可利用拦截器的信息优势,通过利用对来袭目标的估计误差来改善自己的控制策略。

根据微分对策原理,拦截器与来袭目标均寻求相应性能指标的最大化或最小化,且最终对抗目标时寻求偏差e的各分量在任何时刻都为零。则二次型性能指标为

(10)

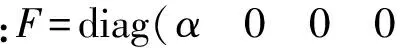
(11)

构造哈密顿-雅克比方程利用伴随原理求解终端状态的方法,根据性能约束(10)式对(9)式进行求解可得

(12)

式中，tgo为待航时间。当目标不机动时,tgo=tf-t,而tf可以有制导初始时刻的相对距离除以相对速度获得。但当目标机动时,所需终止时间会产生较大的计算误差,从而导致待航时间的估计误差。考虑到机动过程中相对距离随时间不断变化,采用滚动时域法,将待航时间用tgo=RAT(t)/vR进行滚动预测,有效避免了待航时间的估计误差。令x=tgo/τA,Z为零效脱靶量,其物理意义为拦截器从当前时刻到制导终止不再输出控制指令,而来袭目标任然按以前的机动方式运动,到制导结束时最终获得的两者之间的最小距离[9]。由庞特里亚金极值原理可得拦截器的微分对策制导最优控制策略为

(13)

为了削弱线性开关函数sgn带来的抖动,用连续函数x/(|x|+δ)来代替符号函数sgn,则拦截器制导律表示为

(14)

转化为拦截器的角速度控制为

(15)

将(12)式代入(14)式并将系数简化,表示为

w*=C1x1+C2x2-C3x3+C4x4+C5x5

(16)

则对应当前时刻的航向角为

(17)

由(16)式可推出具有捕获约束的拦截器的微分对策制导反馈控制原理见图3。

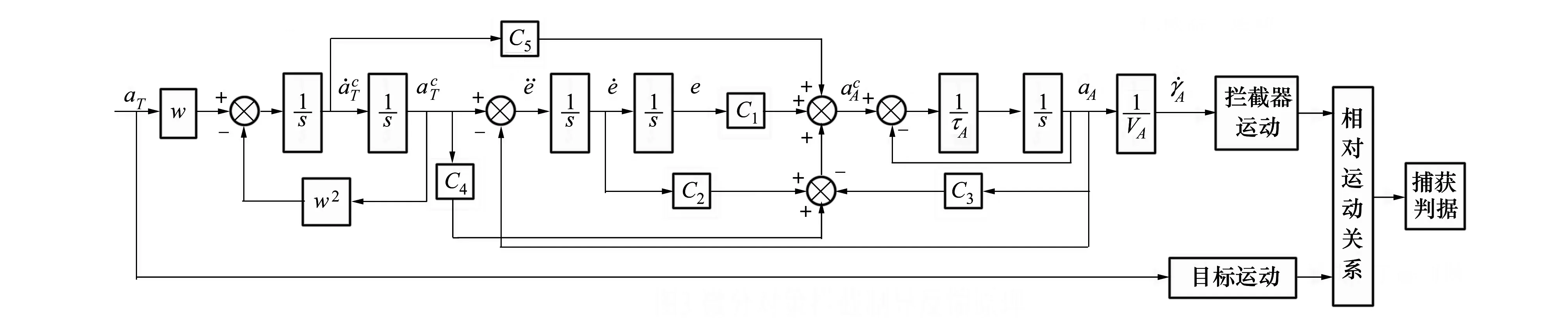
图3 微分对策拦截制导反馈原理

3 仿真分析

假设我方舰艇在初始方位为(0,800)时,发射航速为20kn的拦截器对初始方位为(600,0)航速为20kn的来袭目标进行拦截。考虑到水下探测的难度和目标的机动,选取拦截器的自导扇面半角为60°,当相对距离小于500m时,目标实施蛇形机动规避。假定拦截器有效拦截毁伤半径为10m,为保证来袭目标始终在拦截器的捕获范围内,以有效捕获目标为约束前提进行导引律的设计,对拦截器进行最优导引(OG)和微分对策制导(DG)到导引性能进行仿真比较。

由4图拦截蛇形机动目标运动轨迹可知,来袭目标在航行初始段不机动时,拦截器采用微分对策导引和最优导引的航迹几乎重合。当目标发现拦截器并实施蛇形机动规避时,采用微分对策制导导引可以很好的完成拦截,且末端拦截弹道平直,而采用最优导引时使拦截轨迹发生弯曲而脱靶。

由图5可知,在导引段采用两种制导的跟踪角变化率为0,即在此阶段能操纵拦截器改变速度矢量并力图使其指向瞬时遭遇点。在失稳段,结合图6变化趋势可知,当相对距离趋向毁伤半径时,采用微分对策制导的法向过载趋向0,使拦截器在进入导引头盲距(死区)前使控制面处于中立位置。而最优导引则在相对距离较大时发生脱靶。

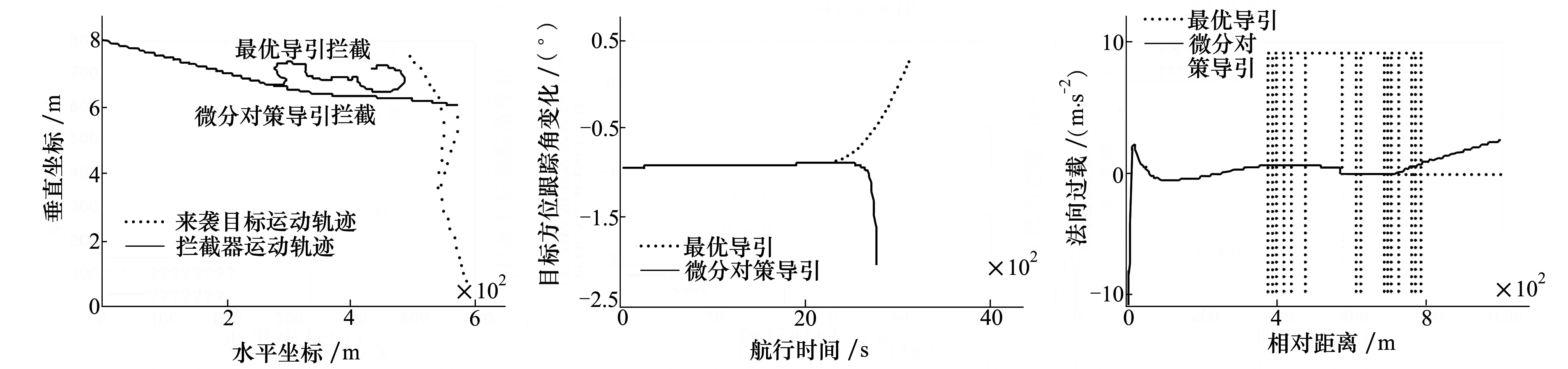
图4 拦截蛇形机动目标运动轨迹 图5 目标方位角跟踪变化趋势 图6 法向过载随相对距离的变化趋势

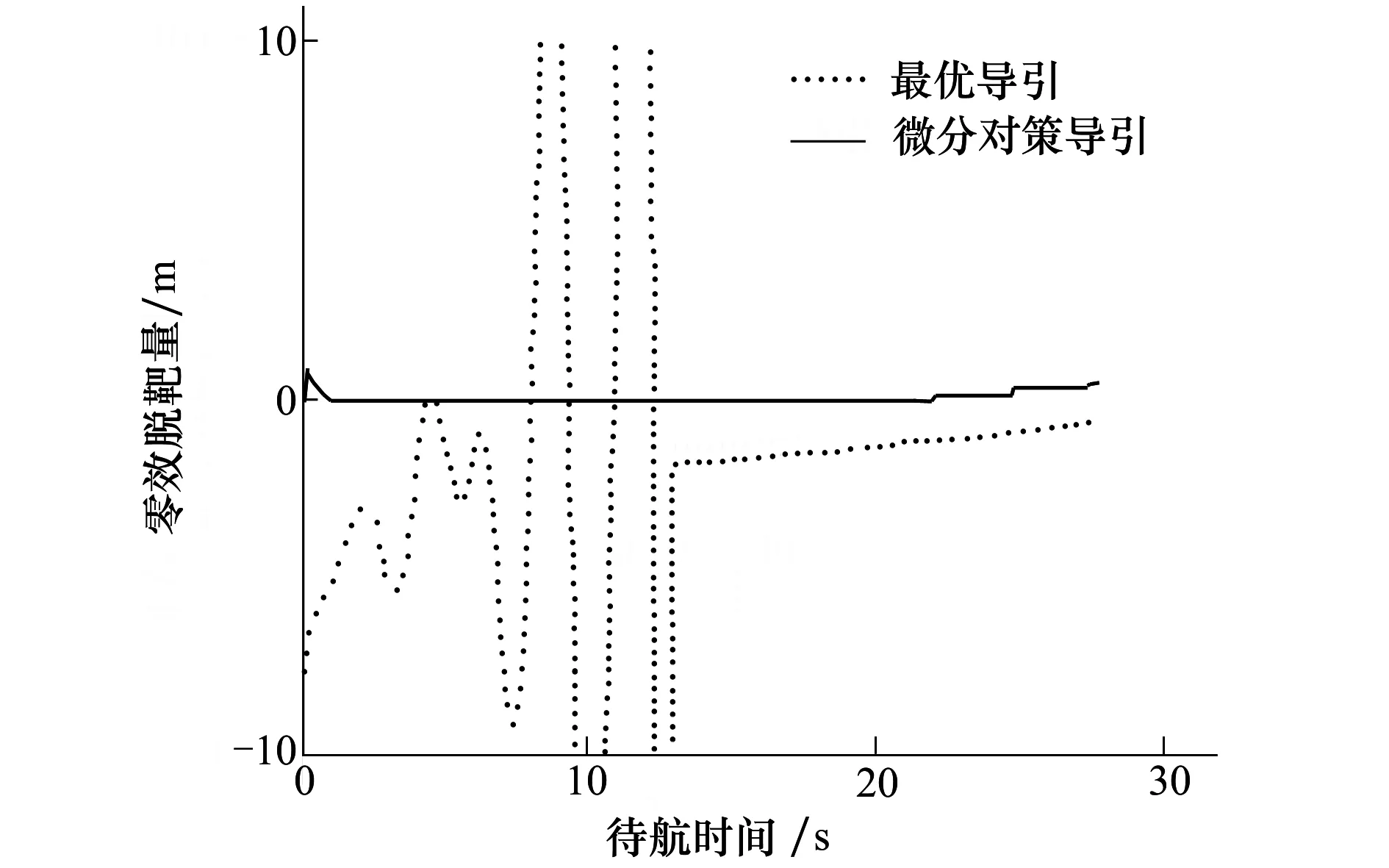
图7 零效脱靶量变化趋势

由图7所示的零效脱靶量变化趋势可以看出,当目标机动时,采用微分对策导引的“零效脱靶量”在初始段进行调整后,保持在零位附近小幅波动,而采用最优导引的零效脱靶量波动剧烈。

当来袭目标分别采用非机动、单纯加速机动和随机蛇形机动方式进行规避时,拦截器采用最优导引与微分对策导引的拦截结果见表1。

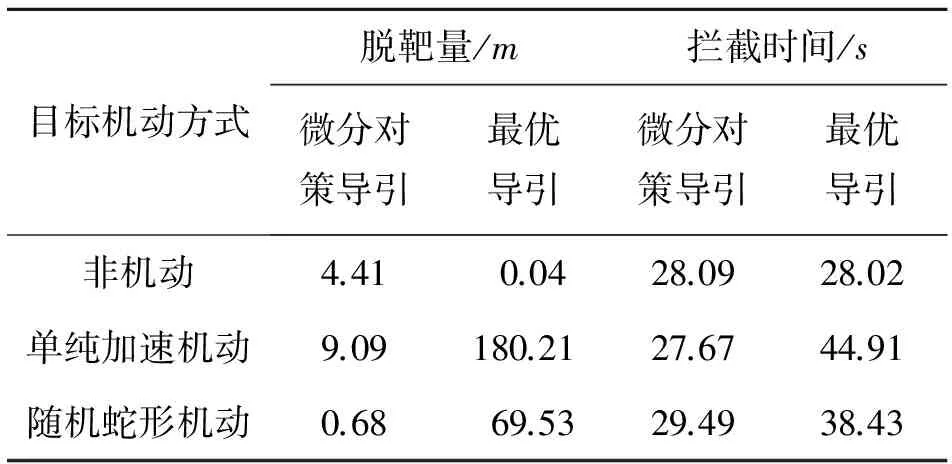
表1 不同机动方式目标的微分对策拦截结果

由表1可知,对于非机动目标,拦截器采用最优导引的拦截效果优于采用微分对策导引所获得的拦截效果,但当目标机动时,最优导引制导效果明显下降。当目标机动单一时,采用微分对策制导可以有效完成拦截任务,相比最优导引具有一定的优势。当目标机动性增强时,采用微分对策进行导引拦截可以在较短的时间实现对机动目标的成功拦截,优势明显。

4 结 论

基于水下目标捕获条件,提出了一种用于水下拦截器迎面拦截的微分对策制导律。

1) 该制导的设计充分考虑水下武器捕获目标的限制,以目标捕获约束模型作为微分对策制导的控制量的饱和约束条件,有效保证了拦截效果;

2) 该制导律的设计以“博弈”对抗理论为基础,以时间和能量消耗为性能指标,利用伴随原理求解终端问题的方法导出作为反馈控制的“零效脱靶量”,并通过滚动时域法对待航时间进行估计,保证了拦截的稳定性和终端命中精度。

3) 仿真结果表明,相对于最优导引拦截,该制导律能实施对来袭机动目标的有效拦截,且目标机动性越强,优势越明显,对工程应用具有一定的参考价值。

[1] 陈春玉. 反鱼雷技术[M]. 北京: 国防工业出版,2006

ChenChunyu.Anti-TorpedoTechnology[M].Beijing,NationalDefenseIndustryPress, 2006 (inChinese)

[2] 方洋旺,伍友利,王洪强,等. 导弹先进制导与控制理论[M]. 北京:国防工业出版社,2015

FangYangwang,WuYouli,WangHongqiang,etal.MissileAdvancedGuidanceandControlTheory[M].Beijing,NationalDefenseIndustryPress, 2015 (inChinese)

[3] 花文华,陈兴林. 高阶控制导弹线性二次型微分对策制导律[J]. 固体火箭技术,2011,34(4):403-407

HuaWenhua,ChenXinglin.LQGDifferentialGameGuidanceLawforHigh-OrderControlledMissiles[J].JournalofSolidRocketTechnology, 2011,34(4): 403-407 (inChinese)

[4] 田进,李言俊. 临近空间防空导弹制导律[J].火力与指挥控制, 2012,37(3): 87-89

TianJin,LiYanjun.ResearchonGuidanceLowforNearSpaceAirDefenceMissil[J].Firecontrol&CommandControl, 2012,37(3): 87-89 (inChinese)

[5]SimoneBattistini,TalShima.DifferentialGameMissileGuidancewithBearing-OnlyMeasurements[C]∥52ndIEEEConferenceonDecisionandControl, 2013: 4218-4223

[6] 石秀华,王晓娟. 水中兵器概论(鱼雷分册)[M]. 西安:西北工业大学出版社,2005

ShiXiuhua,WangXiaojuan.IntroductiontoUnderwaterWeapons(TorpedoBooklet)[M].Xi′an,NorthwesternPolytechnicalUniversityPress, 2005 (inChinese)

[7] 陈颜辉,黄文斌,孙振新. 最优规避鱼雷策略与最小可规避预警距离[J]. 海军工程大学学报,2014,2(26):76-81

ChenYanhui,HuangWenbin,SunZhenxin.OptimalEludingStrategyandMinimalAvoidableAlarmDistanceagainstTorpedo[J].JournalofNavalUniversityofEngineering, 2014,2(26): 76-81 (inChinese)

[8] 李登峰. 微分对策及其应用[M]. 北京:国防工业出版社,2000

LiDengfeng.DifferentialGamesandApplication[M].Beijing,NationalDefenseIndustryPress, 2000 (inChinese)

[9] 雷虎民,张旭,董飞垚,等. 零控脱靶量有限时间收敛制导律[J]. 国防科技大学学报, 2015,3(37):136-142

LeiHumin,ZhangXu,DongFeiyao,etal.FiniteTimeConvergentZero-EffortMissGuidanceLaw[J].JournalofNationalUniversityofDefenseTechnology, 2015,3(37): 136-142 (inChinese)

[10] 孙胜,张华明,周荻. 考虑自动驾驶仪动特性的终端角度约束滑模导引律[J]. 宇航学报,2013,34(1):69-78

SunSheng,ZhangHuaming,ZhouDi.SlidingModeGuidanceLawwithAutopilotLagforTerminalAngleConstrainedTrajectories[J].JournalofAstronautics, 2013,3(37): 69-78 (inChinese)

[11] 陈峰,肖业伦,陈万春. 基于零控脱靶量的大气层外超远程拦截制导[J]. 航空学报,2009,30(9):83-59

ChenFeng,XiaoYelun,ChenWanchun.GuidanceBasedonZeroEffortMissforSuper-RangeExoatmosphericIntercept[J].ActaAeronauticaetAstronauticaSinica, 2009, 30(9): 83-59 (inChinese)

[12] 李运迁. 大气层内拦截弹制导控制及一体化研究[D]. 哈尔滨:哈尔滨工业大学,2011

LiYunqian.IntegratedGuidanceandControlforEndo-AtmosphericInterceptors[D].Harbin,HarbinInstituteofTechnology, 2011 (inChinese)

[13] 郑立伟,荆武兴,谷立祥. 一种适用于大气层外动能拦截器的末制导律[J]. 航空学报,2007,28(4):953-958

ZhengLiwei,JingWuxing,GuLixiang.ATerminalGuidanceLawforExoatmosphericKillVehicle[J].ActaAeronauticaetAstronauticaSinica, 2007,28(4): 953-958 (inChinese)

[14]ShimaT.OptimalCooperativePursuitandEvasionStrategiesagainstaHomingMissile[J].JournalofGuidance,Control,andDymamics, 2011,34(2): 14-25

[15] 张士熊,刘新学,李斌,等. 基于微分对策的拦截末段突防导弹机动突防制导律研究[J]. 导弹与航天运载技术, 2015(2): 81-86

ZhangShixiong,LiuXinxue,LiBin,etal.StudyonManeuverPenetrationGuidanceLawofBallisticBasedonDifferentialGamesinTheTerminalofInterception[J].MissilesandSpaceVehicles, 2015(2): 81-86 (InChinese)

Underwater Active Defense Intercept Guidance Method Based on Differential Game

Cheng Ruifeng1, Liu Weidong1,2, Gao Li′e1,2, Zhang Jianjun1

1.School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China;2.Science and Technology on Underwater Information and Control Laboratory,Northwestern Polytechnical University, Xi′an 710072, China

The differential game guidance law is designed for intercepting the underwater maneuvering target precisely with the constraint conditions that the interceptor must capture the targets in considering of the unpredictability of the actual target maneuver. Based on the differential game theory, the bilateral optimal control quadratic performance index is combined, and the zero miss-distance with the state-feedback is derived by adopting the method of adjoint principle to solve the terminal problem, which can is used as the index of the differential guidance law to control the head angle of the interceptor. The results show that the presented guidance law guarantees perfect intercept for intercept for maneuvering target and has good robustness to target maneuver. Compared with optimal guidance, the different maneuvering target can be intercepted more effectively, which can meet the demand of underwater interception war techniques.

the differential game; guidance law; interception; miss distance

2016-04-06

水下信息与控制重点实验室基金(9140C230202150C23001)与国家自然科学基金(61473224)资助

程瑞锋(1980—)，西北工业大学博士研究生，主要从事水下航行器控制与仿真研究。

TJ63

A

1000-2758(2016)05-0851-06