基于LS-DYNA的真空输纸技术数值模拟

郑俊强 何 林 唐正强

(1.贵州大学机械工程学院,贵州贵阳,550025；2.贵州师范学院,贵州贵阳,550018)



·真空输纸技术·

基于LS-DYNA的真空输纸技术数值模拟

郑俊强1何 林2唐正强1

(1.贵州大学机械工程学院,贵州贵阳,550025；2.贵州师范学院,贵州贵阳,550018)

为提高真空输纸性能,对真空输纸技术中纸张的力学行为进行了模拟分析。由于柔性薄片纸张受力屈曲具有几何非线性的特点,提出了真空输纸技术中纸张力学行为的显式动力学数值分析方法,基于LS-DYNA的壳单元建立了纸张的有限元模型。探讨了不同挺度的纸张在输纸带孔处的应力分布、变形规律及承受侧规拉力的性能。结果表明，随着纸张挺度的增大,真空吸附过程中的纸面应力和隆起变形均减小,而侧规拉力承载能力增强。

真空输纸；LS-DYNA；纸张挺度；力学行为；数值模拟

1 真空输纸技术简介

柔性薄片纸张是生产生活中常用的材料之一,广泛应用于包装、印刷等领域。以纸张为基体的生产加工过程通常需要对纸张进行输送转运,以实现多道工序的作业。真空输纸技术是纸张加工行业最常用的运输方式,其原理如图1所示。气腔底部出气口与真空泵连接,持续抽气形成负压腔。输纸带与表面光滑的输纸板接触,并相对输纸板滑动。当输纸带孔与输纸板孔连通时,输纸带孔处产生负压并吸附其上的纸张与输纸带一起运动。纸张运动过程中受到与运动方向相反的侧规拉力,对纸张进行位置调整和形态梳理。纸张在负压吸附状态下对侧规拉力的承载能力是衡量真空输纸系统性能的关键指标。

已有文献对真空输纸系统在造纸行业的应用进行了研究报道。李晓敏等人[1]对造纸车间的箱纸板机真空系统设计过程进行了介绍。刘斌[2]介绍了透平式真空泵的工作原理及其在现代大型纸机上的应用,并对其节能效果进行了分析。杨五峰等人[3]介绍了新月形纸机的基本结构和真空系统工艺流程特点,阐述了其真空系统的典型配置和工艺设计原则。韩丽娜[4]通过对真空输纸性能的研究,开发出了真空输纸装置的参数化设计软件。H.Kim等人[5]研究了输纸机构的堵塞和同步输纸性能,采用基于因果关系的BP神经网络对实验数据进行分析提取了5个主要变量,并采用非劣优选遗传算法建立了堵塞率和同步输纸率的五变量二阶多项式。Matsumoto Shogo[6]分析了打印机中纸张卷曲现象产生的机理,基于卷曲发生过程建立了纸张卷曲的几何模型,开发出了测量纸张输送过程的速度分布和形变传递的实验装置,定量评价了滚筒形状与纸张卷曲发生过程的关系。Okuna Kenji[7]采用简单的梁单元建立纸张模型来仿真模拟纸张在侧规摩擦力作用下的变形。Umano Hiroshi[8]采用高速输纸实验验证了输纸速度对输纸性能的影响是由于纸张相对于橡胶的滑动速度改变了动摩擦因数。

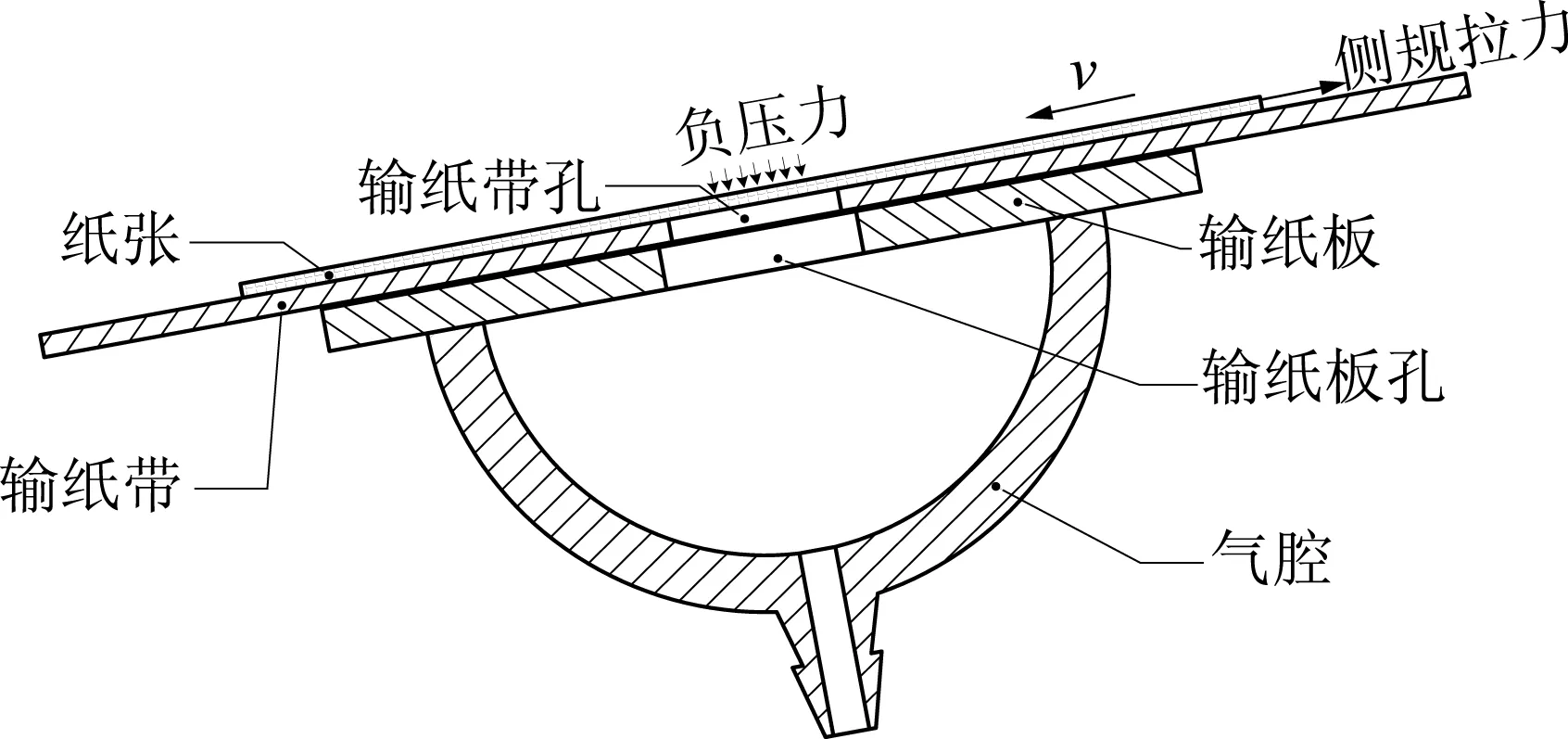
图1 真空输纸装置原理图

由于柔性薄片纸张具有很小的弯曲挺度,其在输纸带孔处的形变属于几何大变形,且在真空输纸装置中很难用实验方法测量输纸过程中纸张的应力状态和屈曲变形。LS-DYNA非线性有限元显式动力学分析技术能够有效地对柔性薄片类材料进行大变形屈曲模拟分析,在安全气囊材料的力学性能研究[9]、柔性管材绕弯成形[10]、薄板轧制过程分析[11]等领域得到了广泛应用。

上述文献对真空输纸技术的研究主要集中在输纸装置的结构以及运行工况对输纸性能的影响方面,对于真空输纸技术中纸张的应力分布、隆起状态及不同挺度纸张的输纸性能差异研究尚未见报道。本文提出纸张力学行为的显式动力学分析方法,采用LS-DYNA壳单元建立真空输纸过程中纸张的有限元模型,对纸张在单个圆孔吸附下负压力加载过程中纸张的应力和隆起状态进行了动态模拟研究,并得到了吸附纸张被拉动的临界侧规拉力,为真空输纸装置的设计提供了理论依据。

2 纸张数值模型的建立

仿真工况：为了研究纸张在真空输纸带上受负压和侧规拉力过程中的力学行为,需对真空输纸装置模型进行简化。使输纸带静止,以忽略输纸速度的影响。采用单孔吸附,负压吸附力简化为吸孔处垂直于纸面的法向压力P,侧规拉力简化为纸张边缘的纸面切向力F,仿真模型如图2所示。仿真过程分两步进行,先在输纸带孔处加载负压P,待纸张形变完全形成后加载随时间线性增加的拉力F。为了更精确地研究载荷施加过程中纸张关键点的应力和位移情况,在纸张模型上选取观测点a,并建立图2所示的坐标系,坐标原点0为圆孔的几何中心,观测点a为x轴与孔边界的交点。

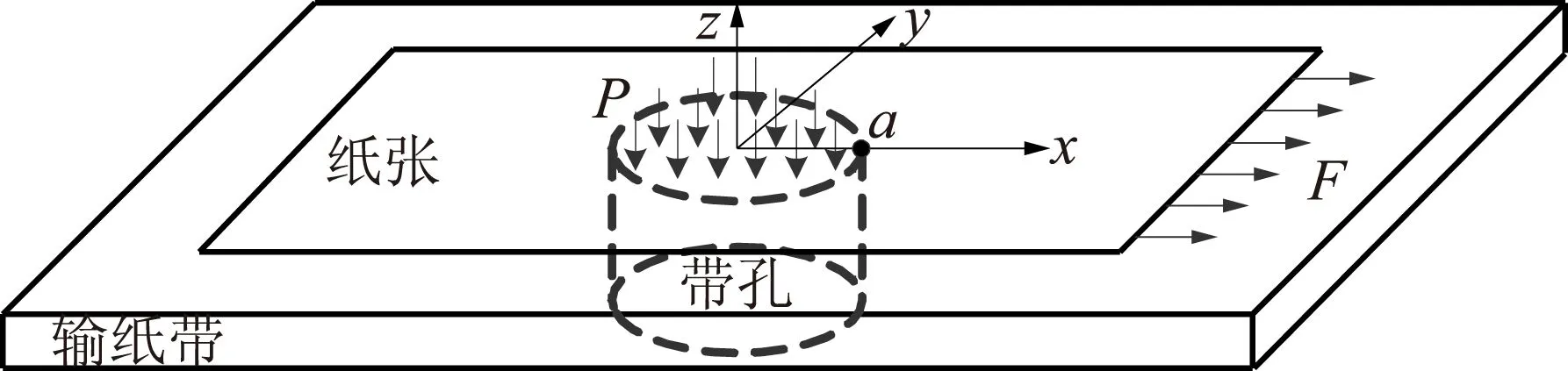
图2 纸张受力模型

由于负压和侧规拉力作用过程中纸张处于弹性变形阶段,因此采用线弹性材料,输纸带的受力和形变不考虑,将其视为刚体,采用10元人民币作为纸张分析模型。当纸张新旧程度或材料不同时,纸张挺度发生变化,表征纸张挺度的物理属性为纸张弹性模量。本实验为研究真空输纸技术中纸张挺度对真空输纸性能的影响,选取弹性模量为1.75、2.00、2.25、2.50 GPa的4组纸张进行仿真实验。纸张和输纸带的其他材料属性如表1所示。

表1 模型的材料属性[12]

采用ANSYS workbench与LS-DYNA联合仿真的方法对纸张加载过程的力学行为进行分析研究。首先,在ANSYS workbench中建立有限元模型并生成计算控制的K文件,然后调用显式动力计算程序LS-DYNA进行计算,将结果导入LS-DYNA专用后处理软件LS-PREPOST进行后处理分析,具体分析流程如图3所示。

图3 纸张数值分析流程

纸张属于薄片材料且具有微小的弯曲挺度,采用shell164壳单元进行网格划分,建立纸张的有限元模型。纸张单元边长1 mm,壳厚0.1 mm。为了保证纸张法向压力加载面与输纸带的孔型一致,纸张几何建模时需设置与孔型相吻合的表面印记,workbench进行网格划分时按照印记形状生成单元和节点。表面印记区域为法向压力加载的关键位置,需对该处进行网格细化以保证计算精度,设置印记处的单元边长为0.5 mm。纸张受力分析过程中,输纸带的刚度行为设置为刚体。为减少计算量,先采用非计算平面四边形单元MESH200建立输纸带的网格平面,再采用SOLID164单元拉伸为网格实体,得到输纸带的有限元模型,输纸带单元边长2 mm。

图4 不同弹性模量纸张的应力分布

接触设置：纸张与输纸带的接触类型为面面接触,接触刚度的罚因子0.1,忽略纸张与输纸带之间的摩擦,考虑纸张壳单元的壳厚影响。约束条件：输纸带固定,约束纸张四条边界的y方向和z方向位移,x方向位移自由,以防止加载过程中纸张翘起及不规则变形。加载方式：在显式动力学分析中,加载载荷为时间的函数,法向压力P及侧规拉力F的载荷曲线分别如式(1)、式(2)所示,分析总时间t=8 ms。

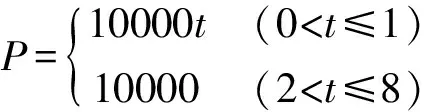
(1)

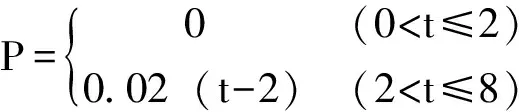
(2)

基于图3的分析流程,将workbench中建立的纸张受力模型生成LS-DYNA计算所需的K文件,对K文件进行修改设置后导入LS-DYNA启动计算。分别建立弹性模量E为1.75、2.00、2.25、2.50GPa的纸张模型进行仿真实验,分析纸张的应力、隆起状态及吸附纸张被拉动的临界侧规拉力。

3 仿真结果与分析

按照上述建立的分析方法,对真空输纸工况下纸张的力学行为进行仿真分析,结果如图4所示。

3.1 纸张应力分析

图4为仿真时间2ms时4种不同弹性模量纸张的应力分布图。此时,10000Pa法向压力加载结束并保持1ms。由图4可知,法向压力加载阶段纸张应力呈环状分布,最大应力发生在纸张与吸孔接触的边界区域,且y方向边界应力略大于x方向边界应力,其次为圆孔的中心区域。当纸张弹性模量E为1.75、2.00、2.25、2.50GPa时,吸孔压力加载完毕后,纸张的最大应力分别为5541、5398、5346、5610Pa。表明当纸张弹性模量从1.75GPa增大至2.50GPa时,真空吸附过程中的纸张最大应力先减小再增大。

图5为仿真过程中观测点a的应力时变曲线。从图5中可以看出,在0～1ms法向压力加载过程中,观测点a的应力值均随着压力的增大而增大,在0～b时刻压力较小时,4条曲线的应力变化一致。b时刻以后,观测点的4条应力曲线均出现波动,并在1ms时分别稳定在不同的应力值。弹性模量E=1.75、2.00、2.25、2.50GPa时,稳定应力值分别为4388.90、4813.69、5103.07、5370.10Pa。2ms时开始加载拉力并线性增大,当拉力未达到临界拉力时观测点的应力仍保持稳定。随着拉力的增大,弹性模量E为1.75GPa和2.00GPa的纸张模型最先出现应力失稳并有较大波动,失稳时刻为5.44ms；弹性模量E为2.25GPa和2.50GPa的纸张模型失稳时刻为5.92ms。表明弹性模量大的纸张,在承受侧规拉力时受力更稳定。

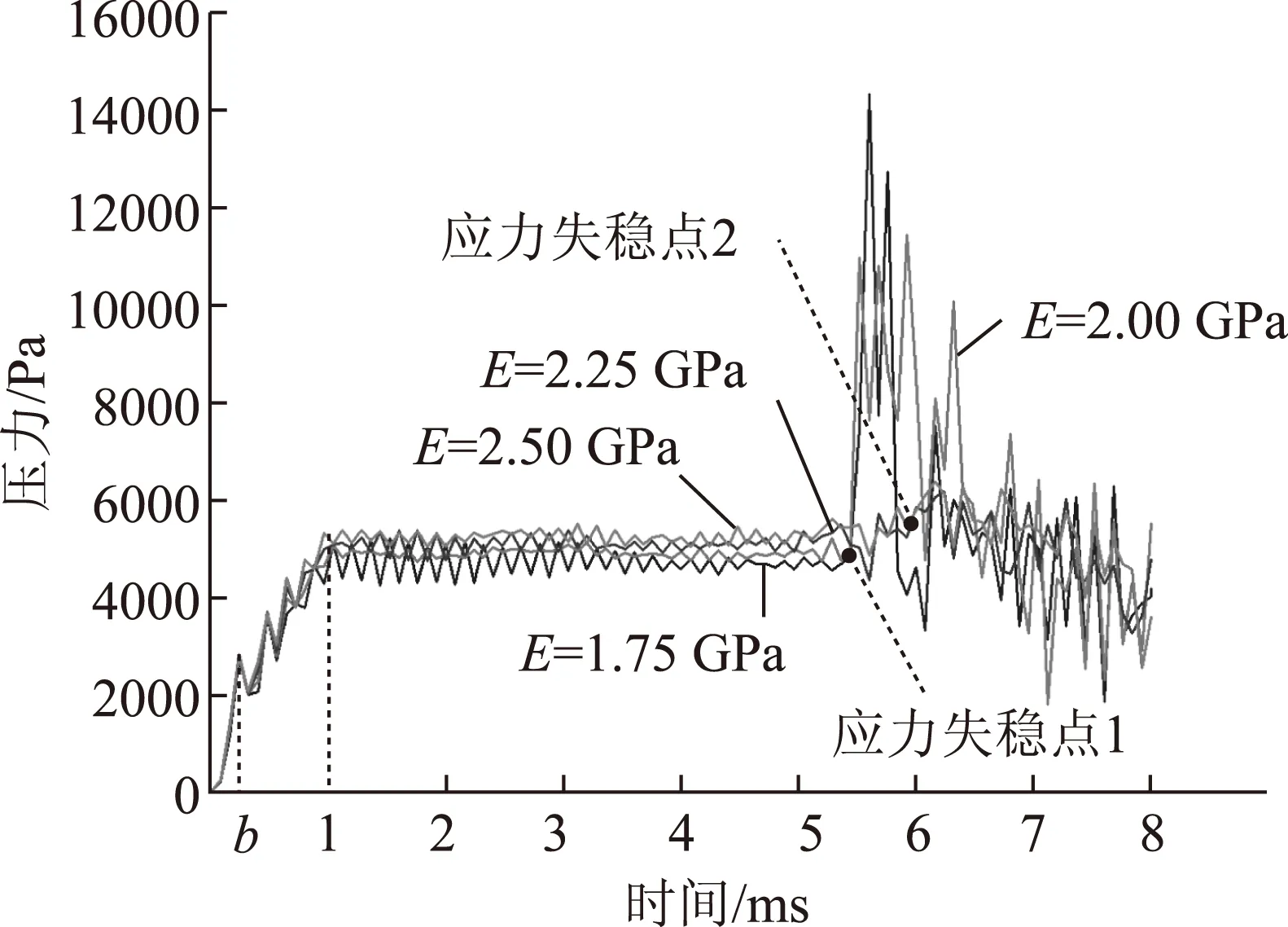
图5 不同弹性模量纸张观测点a的应力时变曲线

图6 不同弹性模量纸张的隆起分布

3.2 纸张隆起分析

图6为仿真时间2 ms时,4种不同弹性模量纸张的隆起分布图,观测指标为z方向位移。由图6可知,当承受吸孔压力时,纸张隆起以吸孔为中心呈圆形面分布,吸孔以外向上隆起,吸孔内部向下凹陷,最大凹陷位置为圆孔中心区域。弹性模量E=1.75、2.00、2.25、2.50 GPa时,纸张的最大隆起分别为0.1358、0.1300、0.1275、0.1256 mm,孔中心的凹陷量分别为0.2683、0.2432、0.2247、0.2177 mm。表明纸张的弹性模量越大,在真空输纸负压加载过程中纸张隆起量越小,纸面越平整。

图7为仿真过程中观测点a的z向位移时变曲线。从图7中可以看出,在0～1 ms法向压力加载过程中,不同弹性模量纸张模型中观测点a的z方向位移均随压力的增大而增大,并在1 ms时刻达到稳定值,且弹性模量越小的纸张,观测点的z方向位移越大。2 ms时开始加载拉力并线性增大,当拉力未达到临界拉力时，观测点的z向位移仍保持稳定。当拉力继续增大,弹性模量E为1.75 GPa和2.00 GPa的纸张模型在5.44 ms最先出现z向位移急速上升,说明此时纸张由吸附状态开始被拉出吸孔,该时刻为吸附纸张被拉动的临界时刻,此时对应的拉力为吸附纸张被拉动的临界拉力；弹性模量E为2.25 GPa和2.50 GPa的纸张模型被拉动的临界时间为5.84 ms。表明吸附纸张可承受的临界侧规拉力随着纸张挺度的增大而增大。

图7 不同弹性模量纸张观测点a的z向位移时变曲线

4 结 论

(1)提出了真空输纸技术中纸张力学行为的显式动力学分析方法,建立了纸张的数值仿真模型。

(2)随着纸张挺度的增大,真空吸附过程中纸面的应力和隆起变形均较小。

(3)纸张挺度越大,真空输纸过程中吸附力越稳定,可承受的侧规拉力越大。

[1] LI Xiao-min, HE Jun, YANG Neng-sheng. Process Design of Vacuum System of the Paper Machine[J]. China Pulp & Paper, 2015, 34(7): 41.

李晓敏, 何 军, 杨能生. 浅谈造纸车间真空系统的设计过程[J]. 中国造纸, 2015, 34(7): 41.

[2] LIU Bin. Application of Turbo-compressor in Modern Paper Machines[J]. China Pulp & Paper, 2012, 31(1): 52.

刘 斌. 透平式真空泵在现代纸机上的应用[J]. 中国造纸, 2012, 31(1): 52.

[3] YANG Wu-feng, MA Ding-quan, ZHANG Rui-qi. Process Design of Vacuum System in the Crescent Paper Machine[J]. China Pulp & Paper, 2012, 31(11): 47.

杨五锋, 马定泉, 张瑞琦. 新月形纸机真空系统的工艺设计[J]. 中国造纸, 2012, 31(11): 47.

[4] HAN Li-na. Properties research and parametric design of vacuum belt paper-conveying device[D]. Xi’an: Xi’an University of Technology, 2008.

韩丽娜. 真空带输纸装置的性能研究及参数化设[D]. 西安: 西安理工大学, 2008.

[5] Kim H, Lee J. Parameter analysis and optimization of paper feeding devices to minimize jamming and simultaneous feeding of multiple pages[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2011, 225(11): 2673.

[6] Matsumoto Shogo, Harada Yoshihiro. Modeling of paper-wrinkle generation process[J]. Nihon Kikai Gakkai Ronbunshu, C Hen/Transactions of the Japan Society of Mechanical Engineers, Part C. 2012, 78(786): 362.

[7] Okuna Kenji, Nishigaito Takaomi, Shina Yasushi. Analysis of paper deformation considering guide friction[J]. Nippon Kikai Gakkai Ronbunshu, C Hen/ Transactions of the Japan Society of Mechanical Engineers, Part C. 1994, 60(575): 2279.

[8] Umano, Hiroshi, Yamaura, et al. Velocity dependencies of paper feeding characteristics[J]. Nihon Kikai Gakkai Ronbunshu, C Hen/Transaction of the Japan Society of Mechanical Engineers, Part C. 2011, 77(778): 2476.

[9] SHEN Bin, REN Sha-sha, JI Peng-kai. Numerical Simulation of the Mechanical Properties for Airbag Fabric Material[J]. Machinery Design & Manufacture, 2012(12): 45.

沈 斌, 任莎莎, 季鹏凯. 安全气囊织物材料的力学性能仿真研究[J]. 机械设计与制造, 2012(12): 45.

[10] ZENG Shan-qi, ZHENG A-li, JIANG Yong. The Analysis for the Influence of Process Parameters on Rotary-Draw Tube Bending Forming[J]. Machinery Design & Manufacture, 2013(12): 213.

曾珊琪, 郑阿黎, 江 勇. 工艺参数对管材绕弯成形的影响分析[J]. 机械设计与制造, 2013(12): 213.

[11] LIU Jie-feng, ZHANG Xiao-ping, ZHAO Chun-jiang, et al. Simulation of the Cold Rolling Strip Crown on the Platform Software LS-DYNA[J]. Machinery Design & Manufacture, 2015(5): 203.

刘杰锋, 张小平, 赵春江, 等. 冷轧板带出口板凸度的显式动力学有限元模拟[J]. 机械设计与制造, 2015(5): 203.

[12] FAN Xian-hu. Dynamic Simulation and Analysis on Picking Bill Mechanism of ATM [D]. Shenyang: Northeastern University, 2011.

范先虎. ATM挖钞机构动力学仿真分析[D]. 沈阳: 东北大学, 2011.

(责任编辑：常 青)

The Numerical Simulation of Suction-tape Feeding Technology Based on LS-DYNA

ZHENG Jun-qiang1,*HE Lin2TANG Zheng-qiang1

(1. College of Mechanical Engineering, Guizhou University, Guiyang, Guizhou Province, 550025;2.GuizhouNormalCollege,Guiyang,GuizhouProvince, 550018)(*E-mail: jqzheng999@163.com)

To improve the performance of suction-tape feeding, the simulation analyses of paper’s mechanical behavior in suction-tape feeding technology was conducted. Considering the geometric nonlinearity of flexible thin paper’s buckling, this article proposed the explicit dynamic numerical analysis method of the paper’s mechanical behavior in suction-tape feeding technology, established the paper’s finite element model based on the shell element of LS-DYNA. The article discussed the stress distribution, deformation law and the performance to resist the side lay’s drawing force of the papers with different stiffness. Results showed that with the increase of paper stiffness, both the paper stress and the ridgy deformation was decreased during vacuum suction, while the ability of resisting the side lay’s drawing force was enhanced.

suction-tape feeding; LS-DYNA; paper stiffness; mechanical behavior; numerical simulation

郑俊强先生，在读博士研究生；主要研究方向：机械装备技术。

2015-11- 10(修改稿)

TH48

A

10.11980/j.issn.0254- 508X.2016.10.010