基于自适应混合网格的脱体涡模拟

2016-11-18张扬张来平赫新邓小刚

航空学报 2016年12期

张扬，张来平，赫新，邓小刚

1.中国空气动力研究与发展中心空气动力学国家重点实验室, 绵阳 621000 2.中国空气动力研究与发展中心计算空气动力研究所, 绵阳 621000 3.中国空气动力研究与发展中心低速空气动力研究所, 绵阳 621000 4.国防科技大学, 长沙 410073

基于自适应混合网格的脱体涡模拟

张扬1,3，张来平1,2,*，赫新1,2，邓小刚4

基于混合网格和CGNS(CFD General Notation System)数据结构，建立了一种各向同性加密/稀疏的网格自适应方法。在悬空点的后处理中，让含有悬空点的单元转化为任意多面体，从而简化了自适应单元剖分模版，同时自适应网格单元之间可完全相容，自适应生成的网格能够直接用于可处理任意多面体的流场求解器。将该自适应方法与脱体涡模拟(DES)算法相结合，开展了65° 后掠三角翼大迎角流动的数值模拟应用，并与初始网格的模拟结果进行了详细比较。对比表明：采用网格自适应方法适当增加局部网格量，能够以较小的成本迅速提高三角翼背风区的空间分辨率，增强数值模拟对小尺度涡系结构的解析能力，从而弥补了基于混合网格的脱体涡模拟中常用二阶格式计算的空间分辨率相对偏低、不利于湍流多尺度结构精细模拟的不足。

网格自适应；脱体涡模拟；非结构网格；混合网格；三角翼；有限体积法

复杂外形的湍流数值模拟对于飞行器设计具有重要意义。当前，湍流数值模拟的主要方法有雷诺平均Navier-Stokes (RANS)方法、大涡模拟(LES)方法、直接数值模拟(DNS)方法以及近年来备受关注的RANS/LES混合算法等。RANS/LES混合算法被认为是现有机器条件下最具潜力的复杂湍流模拟方法[1]，而脱体涡模拟(DES)[2]则是RANS/LES混合算法中的一种杰出代表，它具有模型简洁、便于实施等特点。

对于复杂外形的湍流数值模拟，计算网格的生成是一个关键问题。综合了结构网格和非结构网格优势的混合网格技术无疑是当前和未来的发展趋势[3]，而基于混合网格的DES方法也是当前的研究热点之一[4]。与基本的RANS/LES混合算法思想一样，DES方法通常在边界层内采用RANS模型，这样极大地降低了算法对网格量的需求，另一方面在受关注的分离区等采用了LES模型，希望更精细地模拟湍流的多尺度结构，从而在这些区域需要较密的网格。因此，将DES方法与局部调整网格的自适应技术结合无疑是一种合理的选择，而非结构/混合网格灵活的数据结构天然具有便于自适应方法实施的优势[3]。

大约从20世纪70年代开始，网格自适应相关研究工作逐渐兴起，主要可分为3种实现途径，即所谓的p-type、r-type、h-type。p-type即根据局部流场特性自适应选取不同精度的计算格式；r-type即重新分配网格节点坐标，又称移动网格法；h-type即加密与稀疏网格单元，通过对网格单元的剖分或聚合来改变网格的疏密[5]。

以上方法各有优缺点，在实际应用中针对不同问题采用不同方法或者混合使用，可能会更好地发挥其作用。对于结构网格而言，一般采用r-type 自适应方法，根据流场特性移动网格节点分布，但是这种方法在三维复杂外形情况下的应用受限。从工程实用性来看，非结构/混合网格采用h-type方法相对较优。h-type网格自适应技术早先主要应用于可压缩流Euler方程的求解，其目的是提高流场中变化剧烈的流动特征(如激波等)的捕捉能力[6-7]，随后又逐步推广至基于混合网格的复杂黏性流动数值模拟[8-9]。

本文以CGNS(CFD General Notation System)数据结构为基础，建立了一种混合网格自适应技术，基本单元类型包括四面体、六面体、三棱柱和金字塔，并将自适应技术与脱体涡模拟算法进行了应用结合，主要目的是期望通过网格利用率较高的自适应方法，来弥补混合网格计算中通常采用的二阶格式对于复杂湍流的小尺度运动解析能力稍弱这一不足。通过65° 后掠三角翼自适应前后旋涡流动结构以及物面压力系数分布的对比，对本文这一设想进行了检验。

1 数值计算方法

本文采用了基于混合网格的二阶精度有限体积算法，流场解算器是课题组自主开发的结构/非结构混合计算平台HyperFLOW[10-11]。湍流模型采用了文献[12]提出的DES改进模型(IDDES)。为了降低数值耗散对DES类算法应用的影响，无黏项的离散采用了作者提出的一种适用于非结构算法的自适应耗散调节二阶混合格式。格式构造借鉴了结构算法[13-16]中“中心”格式与“迎风”格式混合的思想，将原始Roe格式的二阶迎风通量与二阶中心格式的通量加权混合，并进一步简化为中心格式通量+可调节的迎风耗散项，即

(1)

在混合格式与自适应网格的结合应用中，发现某些马赫数较高的局部区域计算稳定性稍弱(虽然自适应网格生成过程中已经对网格进行了光滑处理)。为了改善这一情况，借鉴文献[16]的思想，对自适应耗散调节函数进行了改进，即

σ*=1+σΦ-Φ

(2)

式中：σ*为改进的自适应耗散调节函数；Φ为Venkatakrishnan限制器函数，变化范围为0～1，具体形式较为复杂，可参考文献[20]，这里将Φ用于梯度侦测。当σ=1时，表明原耗散调节函数已经需要恢复至1，因此取σ*=1。当σ较小时，Φ的影响比较显著。当Φ=1时，表示限制器不起作用、相应变量变化较为平缓，因此取σ*=σ，即对原算法不做任何调整。当Φ=0时，表示限制器对格式作用最大、相应变量变化较为剧烈，因此取σ*= 1，从而增大格式耗散、增强计算稳定性。

时间推进采用双时间步方法，子迭代采用LU-SGS方法，算法细节可参见文献[21-22]。

2 混合网格自适应技术

2.1 自适应策略

本文选择当前最常用的h-type网格自适应策略。三维基本体单元类型包括三棱柱、四面体、金字塔和六面体(见图1)。初始单元当地数据结构采用了CGNS[23]格式(CGNS包含了一系列规范和约定，数据接口具有较好的通用性，同时CGNS相关软件可免费使用)。通过调用CGNS中级程序库[23]可读取丰富的单元原始信息，有利于自适应相关数据结构的创建。加密单元的剖分方式如图1所示，稀疏为反向操作。为了便于点、面、体单元之间关系的解析，过渡单元和新增单元的当地数据结构同样采用了CGNS格式。

单元剖分类自适应方式的网格单元内通常会产生所谓的“悬空点”，即在某些单元的界面或棱边中心会产生无隶属关系的新点，如图2所示。若通过一些各项异性模版组合来消除“悬空点”，不仅涉及繁杂的剖分方式，而且各向异性加密单元不便于进行多次自适应。另一方面，过少的各项异性模版数量又有可能导致加密传播，进而引起过度加密[8]。本文则简化了后处理，将“悬空点”插入相关的网格单元，使这些单元变化为任意多面体(以六面体为例，如图2所示)。这种处理方式适用于允许任意多面体的求解器。

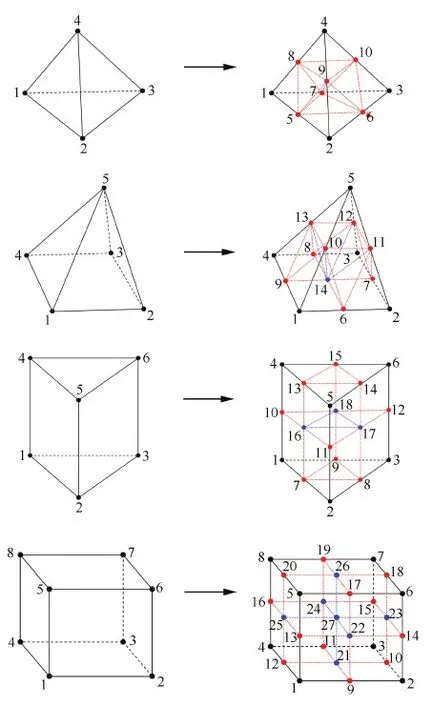
图1 基本体单元加密方式Fig.1 Refinement approach of elementary cells

图2 网格单元“悬空点”的处理Fig.2 Treatment for “hanging node” in cells

为了避免网格单元之间体积差异过大(否则容易导致数值间断)，同时也为了确保网格相容，要求相邻体单元之间的级差不能超过2级(此处的相邻单元特指所有共顶点的单元)。考虑到计算稳定性，进一步光滑了网格单元的疏密过渡，即对于未剖分网格单元的表面相邻单元超过半数被剖分的情况，再将此类单元剖分，如此递归运行直至完全消除这类单元。

以上是网格自适应数据重构的相关操作。最后，只需要针对不同求解器的数据结构特点，解析出所需的关系式即可。对于本文求解器，则需要解析出“表面-体单元”的对应关系[10-11]。

2.2 自适应判据

自适应判据一直以来是网格自适应技术中的一个难点。其困扰在于如何选定加密单元，以及加密到什么程度，其中的关键还是单元误差的合理估计，然而至今还没有一种普适通用的方法。基于流动特征和伴随方程是当前最常用的2种误差估计方法。流动特征方法一般选取流场中特征物理量的梯度作为加密判据。其特点是简单、易行，但只能对误差定性地判断，并不能保证整体误差减小，甚至某些情况下会出现自适应后的数值解更加偏离真解，而且不是所有问题的物理量梯度都存在明显特征。例如超声速激波问题，大梯度主要集中在激波附近，选取压力或密度等物理量的梯度作为自适应判据比较适当，而对于亚声速流动，旋涡区、分离区、附面层之间的梯度都比较接近，因此对加密区域的控制很难把握。基于伴随方程的方法是以目标函数的估计误差为自适应准则，对误差进行定量的判断，比流动特征方法更具合理性，但求伴随解的过程较为复杂，对于非定常变化问题不便于应用。

后文即将开展的三角翼DES模拟算例是完全的亚声速流动，而且背风区的涡核运动是一个非定常变化过程，因此梯度判据和伴随方法实施起来都比较困难。为此本文将问题简化处理，只希望对误差有一个定性的判断，自适应区域将误差可能较大的区域覆盖即可，同时还可避免因非定常变化而调整自适应单元，当然自适应网格量的增长会较快。根据三角翼大迎角流动的特征，低压区集中在涡核及其周围区域，本文采用了背风区的平均压力大小作为特征判据，它与梯度判据的区别在于：不是对误差的直接判断，而是通过间接量辅助地定性查找可能的误差区域。采用平均值则是为了消除因瞬时量不对称引起的自适应后网格不对称。若平均压力小于给定阀值则进行加密，即

(3)

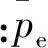
2.3 自适应耦合计算基本流程

前面已经讨论了自适应耦合计算过程中的几个主要内容，再梳理一下它们之间的执行顺序，给出整套算法的基本流程如下：

Step1生成CGNS格式的单块初始网格。

Step2对单块网格进行分区(采用Metis分区)，建立并行分区网格，并初始化各种网格关联信息。

Step3计算分区网格上的流场。

Step4执行网格自适应判据(若需要)，标识需要加密或稀疏的网格单元，合并分区网格及相关信息。

Step5自适应单元分布优化，以保证新网格的相邻体单元之间层级差不超过2级。

Step6加密或稀疏标识单元，同时更新网格关联信息。

Step7生成新的单块网格，重构单元关联信息，重新进行并行分区(采用Metis分区)，重新分配物理量。

Step8计算新的分区网格流场。

Step9判断收敛性或自适应次数，如果未达到要求，返回Step 4，继续进行下一次网格自适应；如果达到要求，程序结束。

上述步骤可描述为原理框图，如图3所示。

图3 网格自适应过程示意图Fig.3 Schematic diagram of grid adaptive procedure

3 65° 后掠三角翼模拟应用

本节以65° 后掠、尖前缘三角翼亚声速绕流来检验网格自适应技术应用于DES类模拟对小尺度涡系运动解析的促进作用。计算模型如图4(a)和图4(b)所示，模型详细情况可参考文献[24]。1996年在NASA Langley NTF 跨声速风洞中开展了此外形的雷诺数、马赫数影响试验研究[24]。计算模拟的状态为来流迎角α=23°、马赫数Ma=0.4、基于平均气动弦长的雷诺数Remac=6×106，此状态下存在旋涡分离和涡破裂等特征流动现象。计算所用时间步长为0.001cr/U∞(cr为气动根弦长，U∞为来流速度)。初始网格如图4(c)所示，单元总数约527万，单元类型包括四面体、金字塔、六面体。物面附近为结构网格单元，背风区采用了较密(相对于迎风面)的非结构网格单元。

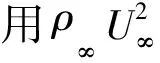
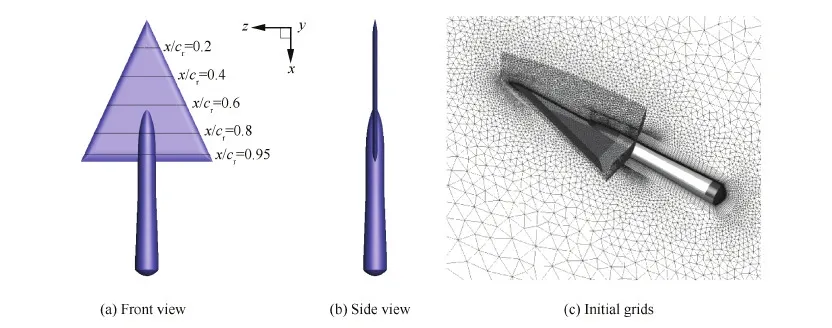
图4 65° 后掠三角翼构型和初始混合网格Fig.4 Geometry of 65° sweep delta wing and initial hybrid grids

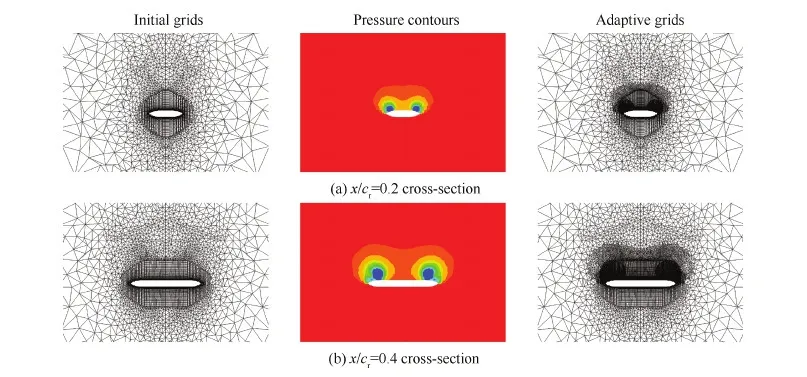
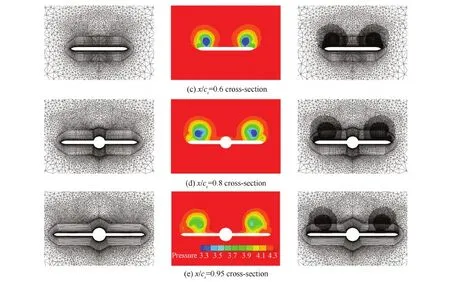
图5 65° 后掠三角翼自适应前后5个截面的网格对比Fig.5 Comparison of initial grids and adaptive grids at five cross-sections of 65° sweep dalta wing

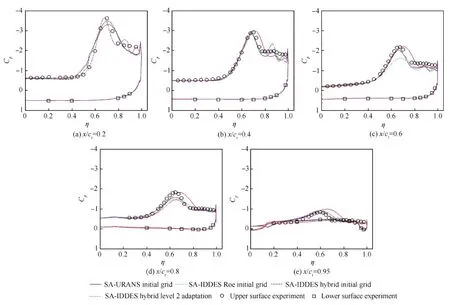
图6 表面压力系数分布计算与试验对比Fig.6 Comparison between calculation and experiment of surface pressure coefficient distribution

为了详细比较自适应前后计算的差异，图6给出了以上5个截面的物面平均压力系数以及相应试验值[24]。在x/cr=0.2站位，自适应后三角翼背风区主涡对应的压力吸力峰更加陡峭，与试验值也更接近，并出现了与二次涡对应的吸力峰，而初始网格计算还没有出现相应的二次吸力峰。在x/cr=0.4站位，初始网格计算也出现了二次吸力峰，其强度略低于自适应网格的对应值。在x/cr=0.6站位，自适应网格计算相应的二次吸力峰已经消失，而初始网格计算相应的二次吸力峰依然存在。在x/cr=0.8站位，自适应网格计算相应的主吸力峰略小于初始网格的对应值，其中一项原因是其主涡核破裂后的涡结构尺度更小、涡量大小和方向更随机，从而进一步削弱了对壁面附近流场的诱导作用。

图6同时还给出了其他计算方式的结果，从图中可以看出，在初始网格上DES类方法与耗散自适应调节混合格式(SA-IDDES+Hybrid)的联合使用，对提高此类复杂湍流问题的数值模拟能力，已经起到了良好的作用。因为在流动最为复杂的背风区，DES主要表现为LES模式，湍流小尺度脉动解析能力优于RANS方法，同时混合格式避免了过多的数值耗散对LES计算的不利影响。在此基础上，与网格自适应技术结合，以较小的成本迅速提高关注区域的空间分辨率，则在一定程度上弥补了二阶混合格式计算的空间分辨率相对偏低的不足，进一步优化了本文湍流数值模拟算法。

图7为自适应前后的瞬时Q涡量等值面。对于初始网格计算流场，主涡核破裂之前呈类似柱体形状，破裂后仍存在较大尺度的涡系结构。对于自适应网格计算流场，主涡核破裂之前已经开始拉伸、扭曲(这种变形源自涡核自诱导)，破裂后变成了许多小尺度涡，并与剪切层失稳形成的小尺度三维结构掺混在一起。

当然，仅凭Q涡量等值面不能完全显示流场的涡系结构差异，为此图8给出了相应截面的涡量云图对比。在x/cr=0.2站位，自适应网格计算相应流场主涡核的内核区涡量更高，自由剪切层的缠绕更紧密，主涡核横截面积更小。在x/cr=0.4站位，自适应网格计算流场的主涡核区开始出现拉伸变形，这与从瞬时Q涡量等值面观察到的涡核扭曲是一致的，自由剪切层虽然受到了这种拉伸影响，但还没有表现出很强的三维特性。在x/cr=0.6站位，自适应网格计算流场的剪切层在卷起过程中受涡核的非轴对称弯扭扰动影响逐渐发展为三维结构，从相应瞬时Q涡量等值面来看，一些小尺度涡系结构被卷入了主涡核，而初始网格计算流场的剪切层依然比较稳定。从x/cr=0.8站位开始，2种计算情况对应的主涡核都已逐渐破裂，自适应网格计算相应破裂区域的涡系结构尺度更小，并可观察到其剪切层中存在小集中涡(或称亚结构(Sub-structure))。

由于自适应网格模拟出的小尺度涡太多，难以看清主涡破裂模态，图9以相应流线形式给出了几种典型的破裂形态，包括螺旋状、泡状、双螺旋状(也可以看作泡状与螺旋状之间相互转换的中间态)。

图7 65° 后掠三角翼自适应前后涡量等值面对比(Q=300)Fig.7 Vorticity iso-surface comparison of initial grids and adaptive grids of 65° sweep delta wing (Q=300)

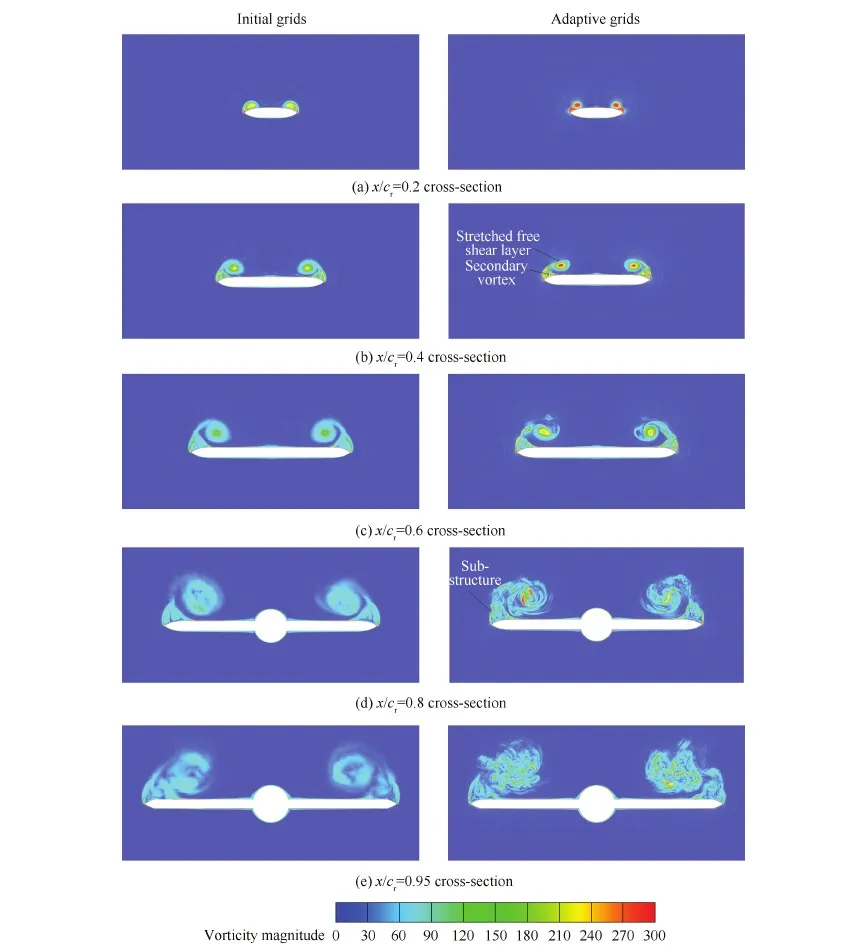
图8 65° 后掠三角翼自适应前后5个截面涡量对比Fig.8 Comparison of vorticity contours on initial grids and adaptive grids at five cross-sections of 65° sweep dalta wing

图9 穿越主涡核区流线对应的3种典型流涡破裂结构Fig.9 Streamlines through main vortex core presenting three typical vortex breakdown structures

4 结论

1) 本文基于混合网格发展了一种h-type各向同性加密/稀疏的网格自适应技术，并实现了与DES类方法的结合应用。

2) 65° 后掠三角翼旋涡流场的数值模拟结果表明，利用自适应方法具有较高网格单元利用率的特性，通过适当增加局部网格量，能够迅速提高受关注区域的空间分辨率，在一定程度上弥补了非结构/混合网格中常用的二阶精度有限体积格式计算的空间分辨率相对偏低的问题，对多尺度湍流问题的数值模拟起到了良好的改善作用。

3) 本文发展的基于混合网格h-type的自适应算法与DES类方法相结合具有良好的工程实用性，可用于复杂外形的湍流数值模拟。需要指出的是，本文网格自适应判据只是根据问题的特征定性地判断，而对于非定常流动如何更合理地判断误差仍是一个比较困难的问题，这也是今后需要努力的方向。

[1] SLOTNICK J, ABDOLLAH K, JUAN A, et al. CFD vision 2030 study: A path to revolutionary computational aerosciences: NASA-CR-218178[R]. Washington, D.C.: NASA, 2014.

[2] SPALART P R, JOU W H, STRELETS M, et al. Comments on the feasibility of LES for wings and on a hybrid RANS/LES approach[C]//Proceedings of 1st AFOSR International Conference On DNS/LES. Columbus: Greyden Press, 1997: 137-147.

[3] BAKER T J. Mesh generation: Art or science?[J]. Progress in Aerospace Sciences, 2005, 41(1): 29-63.

[4] HAASE W, BRAZA M, REVELL A. DESider—A European effort on hybrid RANS-LES modeling[M]. Berlin: Springer, 2009: 19-139.

[5] BAKER T J. Mesh adaptation strategies for problems in fluid dynamics[J]. Finite Elements in Analysis and Design, 1997, 25(3-4): 243-273.

[6] MAVRIPLIS D J. Unstructured mesh generation and adaptivity： NASA-CR-195069[R]. Washington, D.C.: NASA, 1995.

[7] LOHNER R. Adaptive h-refinement on 3D unstructured grids for transient problems[J]. International Journal for Numerical Methods in Fluids, 1992, 14(12): 1407-1419.

[8] MAVRIPLIS D J. Adaptive meshing techniques for viscous flow calculation on mixed element unstructured meshes[J]. International Journal for Numerical Methods in Fluids, 2000, 34(2): 93-111.

[9] SENGUTTUVAN V, CHALASANI S, LUKE E A, et al. Adaptive mesh refinement using general elements： AIAA-2005-0927[R]. Reston: AIAA, 2005.

[10] HE X, ZHANG L P, ZHAO Z, et al. Research and development of structured/unstructured hybrid CFD software[J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2013, 30(S): 116-120.

[11] HE X, ZHANG L P, ZHAO Z, et al. Validation of the structured/unstructured hybrid CFD software—HyperFLOW[C]//The Eighth International Conference on Computational Fluid Dynamics. Mianyang: China Aerodynamics Research and Development Center, 2014: 920-931.

[12] SHUR M L, SPALART P R, STRELETS M K, et al. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities[J]. International Journal of Heat and Fluid Flow, 2008, 29(6): 1638-1649.

[13] TRAVIN A, SHUR M, STRELETS M, et al. Physical and numerical upgrades in the detached-eddy simulation of complex turbulent flows[C]//Advances in LES of Complex Flows. Berlin: Springer, 2004:239-254.

[14] BUI T T. A parallel, finite-volume algorithm for large-eddy simulation of turbulent flow[J]. Computers & Fluids, 2000, 29(8): 877-915.

[15] DENG X B, ZHAO X H, YANG W, et al. Dynamic adaptive upwind method and it’s applications in RANS/LES hybrid simulations[C]//The Eighth International Conference on Computational Fluid Dynamics. Mianyang: China Aerodynamics Research and Development Center, 2014: 807-814.

[16] XIAO L H, XIAO Z X, DUAN Z W, et al. Improved-delayed-detached-eddy simulation of cavity-induced transition in hypersonic boundary layer[C]//The Eighth International Conference on Computational Fluid Dynamics. Mianyang: China Aerodynamics Research and Development Center, 2014: 1055-1073.

[17] 张扬，张来平，赫新，等. 基于非结构/混合网格的脱体涡模拟算法[J]. 航空学报， 2015， 36(9): 2900-2910.

ZHANG Y, ZHANG L P, HE X, et al. Detached-eddy simulation based on unstructured and hybrid grid[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(9): 2900-2910 (in Chinese).

[18] ZHANG Y, ZHANG L P, HE X, et al. Detached-eddy simulation of subsonic flow past a delta wing[J]. Procedia Engineering, 2015(126): 584-587.

[19] ROE P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.

[20] VENKATAKRISHNAN V. Convergence to steady state solutions of the Euler equations on unstructured grids with limiters[J]. Journal of Computational Physics, 1995, 118(1): 120-130.

[21] ZHANG L P, WANG Z J. A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes[J]. Computers & Fluids, 2004, 33(7): 891-916.

[22] ZHANG L P, ZHAO Z, CHANG X H, et al. A 3D hybrid grid generation technique and multigrid/parallel algorithm based on anisotropic agglomeration approach[J]. Chinese Journal of Aeronautics, 2013, 26(1): 47-62.

[23] RUMSEY C, WEDAN B, HAUSER T, et al. Recent updates to the CFD General Notation System (CGNS): AIAA-2012-1264[R]. Reston: AIAA, 2012.

[24] CHU J, LUCKRING J M. Experimental surface pressure data obtained on 65° delta wing across Reynolds number and Mach number ranges: NASA-TM-4645[R]. Washington, D. C.: NASA, 1996.

Detachededdysimulationbasedonadaptivehybridgrids

ZHANGYang1,3,ZHANGLaiping1,2,*,HEXin1,2,DENGXiaogang4

1.StateKeyLaboratoryofAerodynamics,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China2.ComputationalAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China3.LowSpeedAerodynamicsInstitute,ChinaAerodynamicsResearchandDevelopmentCenter,Mianyang621000,China4.NationalUniversityofDefenseTechnology,Changsha410073,China

Anadaptivemeshtechniquewithisotropicrefining/coarseningapproachbasedonCFDgeneralnotationsystem(CGNS)datastructureispresentedandimplementedforhybridgrids.Inordertosimplifythepossiblerefinementcases,elementswithhangingnodesarechangedintopolyhedronandmeanwhilethecompatibilityofthegridismaintained,soflowsolversthatallowpolyhedronscanoperateontheadaptedmesheswithoutanymodifications.Then,detachededdysimulation(DES)methodcombinedwiththegridadaptationtechniqueisappliedtosimulatetheflowovera65°sweepdeltawingathighangleofattack.ThecomparisonoftheDESresultsoninitialgridandadaptivegrid,aswellastheexperimentaldata,iscarriedout.ThenumericalresultsdemonstratethatwiththeuseoftheadaptivetechniquethespatialresolutionintheleewardsideofthedeltawingcanbeimprovedeffectivelyduetotheincrementofcellnumberinsomelocalregionandthecapabilityofpresentDESsolvertoresolvethesmallscaleturbulentflowstructureiseffectivelyenhanced,consequentlytheissueofresolutionisalleviatedinDESsimulationbasedonhybridgridwithacommonlyusedsecond-orderscheme.

gridself-adaptive;detachededdysimulation;unstructuredgrid;hybridgrid;deltawing;finite-volumemethod

2016-01-18；Revised2016-05-09；Accepted2016-06-02；Publishedonline2016-06-141136

URL：www.cnki.net/kcms/detail/11.1929.V.20160614.1136.004.html

s：NationalNaturalScienceFoundationofChina(11532016);NationalKeyTechnologyResearchandDevelopmentProgram(2016YFB0200700)

2016-01-18；退修日期2016-05-09；录用日期2016-06-02； < class="emphasis_bold">网络出版时间

时间：2016-06-141136

www.cnki.net/kcms/detail/11.1929.V.20160614.1136.004.html

国家自然科学基金 (11532016)；国家科技支撑计划 (2016YFB0200700)

.Tel.：0816-2463292E-mailzhanglp_cardc@126.com

张扬，张来平，赫新，等．基于自适应混合网格的脱体涡模拟J．航空学报,2016,37(12):3605-3614.ZHANGY,ZHANGLP,HEX,etal.DetachededdysimulationbasedonadaptivehybridgridsJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3605-3614.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2016.0175

V211.3

1000-6893(2016)12-3605-10

张扬男，博士研究生，工程师。主要研究方向：低速空气动力学计算与试验。Tel.: 0816-2463205E-mail: zhangy29v@sina.com

张来平男，博士，研究员，博士生导师。主要研究方向：计算流体力学、非定常流动机理。Tel.: 0816-2463292E-mail: zhanglp_cardc@126.com

*Correspondingauthor.Tel.：0816-2463292E-mailzhanglp_cardc@126.com