基于滑模控制的航空发动机多变量约束管理
2016-11-18杜宪郭迎清孙浩徐清诗
杜宪, 郭迎清, 孙浩, 徐清诗
西北工业大学 动力与能源学院, 西安 710072
基于滑模控制的航空发动机多变量约束管理
杜宪, 郭迎清*, 孙浩, 徐清诗
西北工业大学 动力与能源学院, 西安 710072
针对航空发动机传统单变量线性控制器min-max切换方法处理约束的不足,提出了单变量滑模控制器替换所有线性控制器的改进策略,并将该方法拓展为新切换逻辑下的多变量滑模控制结构。基于改进的单变量滑模控制器min-max结构,多变量控制策略中加入了多变量滑模主控制器和新的切换逻辑,充分利用发动机的所有控制量,克服了传统方法的保守性,进一步提高发动机约束下的动态性能。对稳态时工作的控制器进行了理论分析,建立了多变量控制器实现精确跟踪的充要条件。仿真结果表明,多变量控制方法在更苛刻的约束条件下能够实现跟踪任务,而且提高了推力跟踪的快速性,调节时间从1.91 s缩短到1.54 s,同时降低了稳态时的油耗。
涡扇发动机; 约束管理; min-max切换逻辑; 滑模控制器; 多变量控制
航空发动机实现跟踪控制的过程中,必须保证各种约束输出量(如温度、喘振裕度、转速和压力等)在允许的工作范围内,否则,会影响发动机的使用寿命,甚至会引发不期望的特性,导致发动机失效,造成严重后果[1-3]。因此,如何在极限保护下发挥航空发动机最佳性能成为其控制研究的关键[4-7]。早在1999年,Spang和Brown[8]就表明航空发动机在运行过程中应尽可能接近其限制值才能发挥最大效能。
传统航空发动机控制系统是由线性控制器经过min-max切换来实现约束管理[8-10]。近年来,研究[11-12]表明,这种min-max线性控制结构在约束处理上具有一定的保守性,阻碍了约束下可能更快的动态响应。Richter等[12-14]提出将min-max下所有线性控制器(主控制器和限制控制器)替换为单变量滑模控制器(SMC),大大改善了原结构的不足。约束输出量在瞬态过程中能够紧贴限制线工作,提高了系统的动态响应性能。但是,改进的方法仍然是基于燃油流量Wf的单变量闭环控制方法。
对于涡扇发动机而言,除了燃油流量计量装置外,还有其他执行机构,例如,可变静子叶片(VSV)和可调放气活门(VBV)。在传统方式下,这2个控制量都是开环控制,根据预先设定的控制律缓慢变化或固定不变[9],并没有得到充分利用。本文旨在将改进的单变量滑模控制方法拓展为多变量 (Wf,VSV,VBV)控制,提出新的切换逻辑,设计多变量滑模调节器,达到充分利用发动机所有执行机构的目的,以期更好的控制效果。
1 传统约束管理不足的反例

图1 传统min-max切换逻辑进行约束管理Fig.1 Traditional min-max switching logic for limit management
传统航空发动机min-max切换逻辑结构如图1所示,期望在各种约束下跟踪所需要的推力。实际中,推力不可测,主控制器(设定点控制器)跟踪能反映推力的风扇转速或发动机压比来间接实现推力跟踪目标。每个约束输出量都有各自对应的限制控制器。主控制器和所有最大值限制器与min切换连接,然后min切换的输出量再与所有最小值限制器经过max切换,选择出最终的燃油流量,实现目标跟踪过程中的约束保护。
图1也是NASA公开发布的某型涡扇发动机控制系统结构图,其中约束管理部分具体包括转速(Nf,Nc)限制器、燃烧室压力(Ps30,Ps3)限制器、发动机加速(Accel)限制器,以及油气比(RU=Wf/ Ps3)限制器。加速限制器的作用是防止加速过快而引发高压压气机喘振或者涡轮温度超限,影响发动机的安全性。RU限制器的目的是在发动机减速过程中避免发生低压压气机失速或燃烧室贫油熄火[10]。
本研究的发动机控制目标是跟踪风扇转速Nf期望值,并保证约束输出量在预设的限制范围内。对于本例,简单起见,仅考虑高压涡轮出口温度T48的最大值限制[14]。主控制器(Nf)和最大值限制器(T48)通过min切换逻辑相连。
快速响应一直是航空发动机动态性能的一个关键指标[4,7]。针对传统基于线性控制器的min-max切换结构,尝试通过增加主控器的带宽来增加整个系统的响应速度。
运行非线性发动机模型C-MAPSS40k[15]自带的线性化工具包,得到地面慢车状态的小偏离线性模型为:

(1)
(2)
(3)
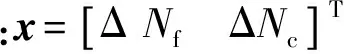

对这6个主控制器进行仿真,控制效果对比结果如图3所示。

图2 6个主控制器下系统的闭环带宽Fig.2 Closed-loop bandwidth for 6 main regulators

图3 传统约束管理方法示例Fig.3 Example of traditional limit management method
由图3可知,随着带宽增加,ΔNf动态响应最初明显变快,很快趋近其可达到的最大值。ΔNf最短调节时间大约是1.86 s,再进一步增加带宽并不能增快系统的动态响应。但是,当ΔNf响应速度最快时,约束输出量ΔT48在瞬态过程中并没有达到它所允许的限制值200°R。
图3(c) 是切换标志,其值为1指ΔNf主控制器被激活,为了表明ΔT48限制器被激活。观察可得,对于6个主控制器,min切换逻辑下ΔT48限制器都在t=0时被激活,说明初始时ΔT48限制器的控制量小于主控制器的控制量。但t=0时刻温度限制器被激活时,温度输出量还远未达到其限制值。
该反例揭示了线性控制器min-max切换逻辑结构具有如下不足:一方面,瞬态过程中约束输出量未触及其限制线,约束未能得到充分利用;另一方面,约束输出量还未达到其限制值时相应限制器就过早被激活,限制了主控制器本应更快的动态响应。
2 单变量滑模控制器min-max切换方法
借鉴文献[12-14],将传统min-max切换逻辑中的线性控制器,包括主控制器和所有限制器,都替换为单变量滑模控制器(SMC)。限于篇幅,单变量SMC方法不再赘述,得到主控制器的控制律表达式[12]为
u1r=-G(Ax+Bu1)-ηsgn(s)
式中:u1r为控制量速率;G为滑动模态增益矩阵;切换增益η直接影响动态响应速度。
为了更好地比较控制效果,仿真采用与第2节反例中完全相同的发动机模型。假设控制目标仍然是跟踪风扇转速变化值150 r/min,但施加更严格的温度限制值150°R,通过增加主控制器切换增益η研究所能达到该约束下最快的动态响应。研究η从1变化到6的仿真效果,如图4所示。
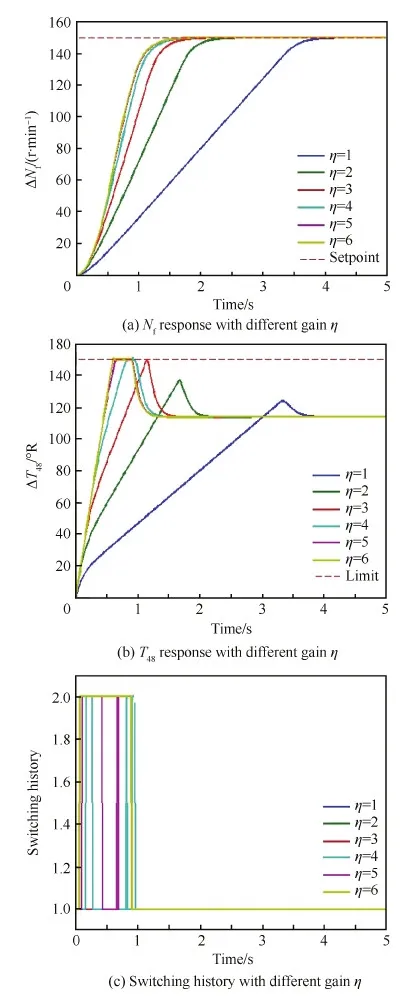
图4 基于单变量滑模方法的约束管理示例Fig.4 Example of limit management based on single-input sliding-mode method
由图4(a)可知,随着主控制器切换增益η的增大,风扇转速ΔNf的动态响应逐渐变快,最后达到最快的调节时间大约是1.08 s,相较于线性控制器min切换结构下的1.86 s,滑模控制器大大提高了响应速度。观察图4(b),随着η增大,ΔT48瞬态过程中的最大值逐渐增加直至其最大限制值,并被约束在限制线处。图4(c)表明,当ΔT48接近其限制线时,限制器才替代主控制器起作用。
通过上述比较分析,min切换逻辑下的滑模控制器可以充分利用约束,提高了系统动态响应速度。但是,这种改进方法仍然是仅考虑燃油流量ΔWf作为控制量的单输入情况,属于单变量控制。
3 多输入滑模控制器的约束处理研究
基于改进的min-max切换下单变量滑模控制器,设计多输入(Wf,VSV,VBV)控制器实现约束管理。
考虑带有积分的航空发动机多输入模型,其状态空间描述为
(4)
式中:x=[ΔNfΔNc]T;u3=[ΔWfΔVSV ΔVBV]T
所有输出量可定义为
yi=Cix+Diu3
(5)
式中:i=1,2,…,h;Ci是一个1×n向量;Di是一个1×m向量。
(6)


3.1 设计原理及关键参数
所设计的多变量滑模控制器由3部分组成,如图5所示:主控制器(多变量滑模控制器)、约束管理部分(保留了改进的min-max切换下单变量滑模限制器)以及切换决断与平滑过渡部分(给切换信号并确保主控制器和限制管理部分的平滑过渡)。
1) 主控制器
所设计的主控制器是基于状态空间模型的多变量滑模控制器[17],并由状态反馈控制器为其提供状态参考值。多变量滑模控制的核心思想是将状态轨迹引到滑模面上,且一旦到达滑模面后能够维持在滑模面上[18]。

图5 多输入约束管理结构Fig.5 Principle structure for multi-input case
假设目标是跟踪状态参考值,即
(7)
则跟踪误差为
(8)
s=Ge
(9)
式中:G为增益矩阵,直接关系到滑模态的动态特性,本文通过常规QR分解法[19]设计参数G。
根据滑模控制机理,要求状态轨迹在有限时间内到达滑模面s=0。可达性条件可表示为

(10)
式中:“Ξ”是一个包含3个切换增益ηi(i=1,2,3)的对角矩阵;sgn(s)是由sgn(si)组成的向量。
滑模控制有一个显著的理论缺陷,在滑模面附近会出现非常快速的切换,称作抖振现象[19]。为减小抖振现象,本文采用连续双曲正切函数[20]tanh(kisi)代替不连续符号函数sgn(si)。式中:ki>0,是设计参数,决定tanh(·)在零点附近的斜率。因此,式(10)可表示为
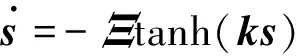
(11)
式中:k是ki构成的向量。
上述设计可以实现状态对参考值的跟踪,但实际中需要实现输出量的跟踪,而不仅是状态量。引入参考模型,旨在为多变量滑模控制器提供合适的状态参考值,从而实现输出量跟踪的目标。因为有3个控制量,主控制器可实现3个输出量的跟踪,而航空发动机控制目标仅需跟踪1个主输出量y1(Nf),因而,可从约束输出量中任意选取2个作为主控制器的辅助跟踪量。注意,这2个辅助跟踪量本质上仍然是约束量,也必须包含在约束管理部分。
参考模型可定义为
(12)
北美刺龙葵是玉米田、粮食作物、西红柿地、牧场、荒地的主要问题杂草,也是一些重要害虫和农作物致病菌的中间寄主,如番茄叶斑真菌(tomato leafspot fungus)、番茄斑枯病(Septoria lycopersici)、马铃薯和番茄花叶病毒的寄主。入侵农田后可造成农作物减产 35%~60%[3-4]。在美国南部几个州,北美刺龙葵被列为10种问题杂草之一,是降低玉米田和牧场产量的主要有害生物。
针对参考模型的状态反馈控制律可定义为
ur=-Kxa+Pr
(13)
式中:K为反馈增益;P为静态前置滤波器;r为参考值向量。为了保证所提供的状态参考值能使多变量滑模控制器输出量跟踪到其参考值(证明见3.2节),矩阵P定义为

(14)
2) 限制管理部分
该部分由多个单变量滑模限制器与min-max切换逻辑相连组成,完全保留了第3节中的约束管理部分。单变量滑模控制器的滑模变量定义为约束输出量与其极限值的差值。因此,对于任意的滑模约束管理器,单独在闭环回路中工作的话,相应的约束输出量都会在有限时间内到达其限制值,且没有超调量,保证瞬态过程绝不会超限。
3) 切换决断及平滑过渡部分

图6 切换决断部分的逻辑流程Fig.6 Flowchart for new switching logic
切换信号σ可以表示成约束输出量的函数
σ(k)=ψ(y(k),δ)
(15)
式中:δ为停留时间,δ>0表示限制器部分被激活后必须停留的时间,y(k)为约束输出量,函数关系ψ描述如下:在正常情况下,σ=1,这时多变量滑模主控制器和发动机构成闭环回路工作。然而,当存在任一约束输出量超过其限制值时,σ=2,激活限制器部分。一旦限制器部分工作,必须停留一个预先设定的时间(称作停留时间[21-22])。当停留时间δ结束后,σ=1,激活主控制器工作。此控制模式反复进行。
毋庸置疑,停留时间δ对动态响应和约束管理有着重要影响。本文通过试验法得到了不同飞行条件下的停留时间δ和系统响应快慢的关系。
在不同的飞行条件下,仅仅改变参数δ的值,从0逐步增加到1.5 s(增量为采样时间Ts=0.015 s[15])。对于每个δ值,计算ΔNf的调节时间。所有情况下,存在最优的δ值,使调节时间最短,动态响应最快。限于篇幅,图7只给出几例不同飞行条件下的仿真效果。尽管图中曲线存在波动,但停留时间δ对响应速度的影响趋势是一致的,通过数值计算可以直接得到δ的最低点极值,这时对应的主输出量有最快的动态响应。这种情况很容易理解:如果δ太大,限制器工作的停留时间大大超过了其必要时间,从而限制了主控制器的更快的动态响应;如果δ太小,主控制器和限制器部分切换过于频繁,破坏了主控制器和限制器的基本功能。
主控制器有3个控制量,而限制器部分仅有1个控制量,因此当限制器部分被激活时,其余2个控制量速率设为0,即VSVr=0,VBVr=0。即,当限制管理部分工作时,除Wf外的其他控制量都固定为切换前一时刻的值保持不变。仅Wf在主控制器和限制器间平滑过渡,其平滑切换律可定义为
u1=ub+(ua-ub)e-αt
(16)
式中:ua为切换前一时刻的控制量值;ub为切换后随时间变化的实时控制量;时间常数α∈[0,+∞)。α的选取需要考虑快速瞬态响应和限制保护的相对重要性,折中选择合适的参数值。

图7 不同飞行条件下停留时间与调节时间的关系 Fig.7 Relationship between dwell time and settling time at different flight conditions
3.2 确定稳态时工作的控制器
针对所提出的新切换逻辑下的多输入控制器,分析了稳态时的2种工作情况。为了实现跟踪任务,期望在稳态时主控制器处于激活状态。下面首先建立稳态时主控制器工作的充要条件。
1) 稳态时主控制器工作的条件
首先证明在稳态时状态量跟踪误差以及输出量跟踪误差都为0。
假设1矩阵GBa是可逆的。
整理式(8)~式(10),可得到
(17)
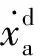
(18)
可推导出处于滑模态s=0时的系统跟踪误差动态响应为
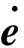
(19)
式中
Aeq=(Aa-Ba(GBa)-1GAa)
(20)
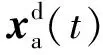
(21)
式中:vr(t)是某一任意输入速率,稳态时为0。
将式(21)代入式(19)中,化简可得
(22)
假设2设计滑模系数G将Aeq的极点配置在左半平面,实现稳态滑模面。Aeq可被视作Aeq=(Aa-BaK′),其中K′=(GBa)-1GAa,可直接进行极点配置。
因此,式(22)状态量跟踪误差的渐进收敛性得到保证,且稳态时为0,有
(23)
式中:下标“a_steady”表示增广状态稳态值。
vr=-K·xa+P·r
(24)
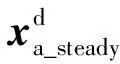
(25)
在稳态时,可得跟踪输出量yj(j=1,2,3)为

(26)
将式(25)代入式(26)中可得
yjss=rj=1,2,3
(27)
式中:下标“ss”表示稳态时的输出量。
通过上述分析推导,证明3个跟踪输出量稳态时精确跟踪到设定点参考值。
假设在稳态时主控制器保持活跃,可根据xa_steady得到系统其他输出量的稳态值为
yjss=Caj·xa_steadyj=4,5,…,h
(28)
式中:Caj是Ca的第j行。
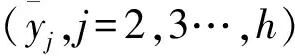

(29)
2) 稳态时因约束限制的控制效果
若稳态时式(29)不成立,即,存在约束输出量j=2,3…h,使以下不等式关系有一个成立
(30)
这种情况下,稳态时存在限制器被激活的现象。基于切换决断部分所设计的逻辑,在滑模限制器工作δ时间后,主控制器被强行激活进行再判断。因此,最终因约束限制的控制效果将会在主控制器和限制器部分频繁切换,当然也无法实现跟踪任务。
4 多变量与单变量滑模控制器对比分析
针对C-MAPSS40k不同飞行条件(如地面慢车、空中慢车、最大巡航以及最大起飞等)的发动机模型设计了新切换逻辑下的多输入控制器,并仿真验证了各种状态下多变量控制器在同时实现推力跟踪及约束管理上的有效性。所有情况下,转速能够快速地跟踪其期望值,且瞬态过程中约束输出量紧贴其限制线工作,表明所提出的多输入方法能够充分利用所有控制量及约束限制,最大限度地发挥发动机的潜能。本节以地面慢车状态为例,对比了所提出的多输入控制器和第2节的基于min-max结构的单变量滑模控制器的控制效果。
为了使对比有意义,两者使用相同的限制器和相同状态的发动机模型,并实现相同的控制目标。风扇转速Nf为主输出量,简单起见,这里仅考虑2个约束输出量:T48上限约束和高压压气机喘振裕度smHPC下限约束。值得说明的是,所提出的方法可用于任意数量的约束输出量。
地面慢车状态的多输入发动机模型[15]矩阵A,B,x,u,C和D为


x=[ΔNfΔNc]T
u=[ΔWfΔVSVΔVBV]T


研究表明,所设计的多变量方法比单变量方法具有两个明显的优点,示例进行说明。
4.1 优势1
多变量控制方法可以实现更广的控制目标。对于本例,2种方法相同的控制目标是:跟踪风扇转速变化量ΔNf=400 r/min,同时在瞬态过程中满足ΔT48≤200°R,以及ΔsmHPC≥-10%。参数设置δ=0.15 s (10×Ts),α=20。2种控制器的仿真结果如图8所示。图中的点划线表示单变量滑模控制效果,主输出量ΔNf并不能跟踪其期望值400 r/min。因为仅有燃油流量ΔWf一个控制输入量,实际上,使ΔNf达到400 r/min时所需要的ΔWf,将会使约束输出量ΔT48超过其限制值200°R。由于限制器的作用,稳态时ΔT48被约束在200°R限制线处,此时所耗的ΔWf也将ΔNf局限在340 r/min左右。对于本例,单变量min-max切换滑模控制器约束下无法实现跟踪任务,稳态时限制器工作。
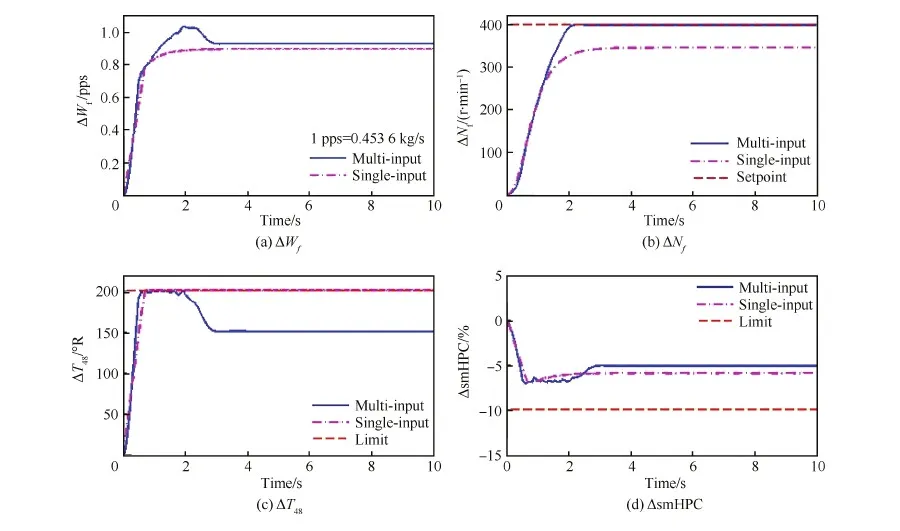
图8 多变量控制器和单变量滑模控制器动态响应对比(ΔNf=400 r/min, δ=0.15 s) Fig.8 Dynamic response contrast of multi-input controller and single-input sliding controller(ΔNf=400 r/min, δ=0.15 s)
相反地,多输入控制方法能够在约束保护下实现精确的指令跟踪,如图8中的实线所示。约束下ΔNf的调节时间是1.92 s左右,ΔT48在瞬态过程中沿着限制线工作,ΔsmHPC在整个过程中都维持在约束内。显然,额外的控制自由度提高了发动机控制系统在大范围条件下工作的能力。多变量滑模控制器相较于单变量滑模控制器以更大范围地同时实现跟踪目标和约束保护任务。
4.2 优势2
对于2种方法都能够实现的控制目标,多变量方法可以在更小的油耗下,实现更快的动态响应。
对于本例,保持约束输出量ΔT48,ΔsmHPC和4.1节中的限制值相同,考虑一个比4.1节要容易实现的跟踪目标,使2种方法都能够实现,这里选择ΔNf增量为300 r/min。仅改变参数δ=0.30 s (20×Ts),得到多变量、单变量控制器仿真对比结果如图9所示。

图9 多变量控制器和单变量滑模控制器动态响应对比(ΔNf=300 r/min, δ=0.30 s) Fig.9 Dynamic response contrast of multi-input controller and single-input sliding controller(ΔNf=300 r/min, δ=0.30 s)
如图9所示,2种方法在稳态时都是主控制器工作,实现设定点的跟踪目标,且在瞬态过程中,约束输出量都维持在各自的限制内工作。对于本例,多变量控制方法和单变量滑模控制方法都能很好地实现主输出量跟踪与约束保护目标。
基于新切换逻辑的多变量控制方法在约束下的动态响应效果有明显的提高。一方面,多变量控制方法的ΔNf调节时间是1.54 s左右,而单变量滑模控制方法是1.91 s左右,表明多变量控制方法在相同的控制目标下具有更快的动态响应;另一方面,在稳态时,多变量控制方法所耗的燃油流量ΔWf比单变量方法要小。这是因为多变量滑模主控制器除了ΔNf外还考虑了辅助跟踪输出量ΔT48和ΔsmHPC,可以设定他们的稳态参考值。而对于单变量方法,稳态时ΔT48和ΔsmHPC的值是固定的,由所期望的ΔNf参考值决定。从航空发动机长期工作的角度来看,较低的油耗将获得重大的经济效益。
5 结 论
1) 所改进的min-max切换下的单变量滑模控制方法和传统线性控制器相比,能够充分利用约束,达到更快的动态响应。在相同的控制目标下,调节时间从1.86 s缩短到1.08 s。
2) 多变量滑模控制器和min-max下的单变量滑模方法相比具有明显优势,一方面在更严格的约束条件下也能够实现跟踪任务;另一方面在同样的目标下,达到更快的响应速度,调节时间从1.91 s缩短到1.54 s,且具有燃油经济性。尽管本文仿真仅涉及2个限制器,分析表明,该方法可以拓展到任意数量的限制器。
3) 基于新切换逻辑的多变量控制器比传统的min-max线性控制器在约束处理和动态响应上都有显著的改进。
[1] JAW L, MATTINGLY J D. Aircraft engine controls: design, system analysis, and health monitoring[M]. Reston: AIAA Education Series, 2009: 96-117
[2] THOMPSON A, HACKER J, CAO C. Adaptive engine control in the presence of output limits: AIAA-2010-3492[R]. Reston: AIAA, 2010.
[3] 杜宪, 郭迎清, 陈小磊. 基于非线性模型预测控制方法的航空发动机约束管理[J]. 航空动力学报, 2015, 30(6): 1766-1770.
DU X, GUO Y Q, CHEN X L. Limit management of aircraft engine based on nonlinear model predictive control method[J]. Journal of Aerospace Power, 2015, 30(6): 1766-1770 (in Chinese).
[4] LITT J S, FREDERICK D K, GUO T H. The case for intelligent propulsion control for fast engine response: AIAA-2009-1876[R]. Reston: AIAA, 2009.
[5] GIBSON N. Intelligent engine systems: NASA/ CR-2008-215240[R]. Washington, D.C.: NASA, 2008.
[6] CSANK J T, MAY R D, LITT J S, et al. A sensitivity study of commercial aircraft engine response for emergency situations: NASA/TM-2011-217004[R]. Washington, D.C.: NASA, 2011.
[7] 王旭, 梁钧襄. 有约束的航空发动机加速最优控制[J]. 航空学报, 1992, 13(4): 144-150.
WANG X, LIANG J X. Study on optimal acceleration control of constrained jet engine based on nonlinear programming[J]. Aata Aeronautica et Astronautica Sinica, 1992, 13(4): 144-150 (in Chinese).
[8] SPANG H, BROWN H. Control of jet engines[J]. Control Engineering Practice, 1999, 7(9): 1043-1059.
[9] MAY R D, CSANK J, LAVELLE T M, et al. A high-fidelity simulation of a generic commercial aircrafts engine and controller: AIAA-2010-6630[R]. Reston: AIAA, 2010.
[10] CSANK J, MAY R D, LITT J S, et al. Control design for a generic commercial aircraft engine: AIAA-2010-6629[R]. Reston: AIAA, 2010.
[11] MAY R D, GARG S. Reducing conservatism in aircraft engine response using conditionally active min-max limit regulators: NASA/TM-2012-217814[R]. Washington, D.C.: NASA, 2012.
[12] RICHTER H. Multiple sliding modes with override logic: limit management in aircraft engine controls[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(4): 1132-1142.
[13] RICHTER H, LITT J S. A novel controller for gas turbine engines with aggressive limit management: AIAA-2011-5857[R]. Reston: AIAA, 2011.
[14] RICHTER H. A multi-regulator sliding mode control strategy for output-constrained systems[J]. Automatica, 2011, 47(10): 2251-2259.
[15] MAY R, CSANK J, LITT J S, et al. Commercial modular aero-propulsion system simulation 40k (C-MAPSS40k) user’s guide: NASA/TM-2010-216831[R]. Washington, D.C.: NASA, 2010.
[16] 吴君凤, 郭迎清. 发动机稳态与过渡态控制集成设计仿真验证[J]. 航空动力学报, 2013, 28(6):1436-1440.
WU J F, GUO Y Q. Design and simulation of aero-engine steady-state and transient-state control integration[J]. Journal of Aerospace Power, 2013, 28(6): 1436-1440 (in Chinese).
[17] DU X, RICHTER H, GUO Y Q. A MIMO sliding mode approach to limit protection in aero-engines DSCC2015-9634[C]//Proceedings of the ASME 2015 Dynamic Systems and Control Conference. New York: ASME, 2015.
[18] RICHTER H. Advanced control of turbofan engines[M]. New York: Springer, 2012: 148-169.
[19] EDWARDS C, SPURGEON S. Sliding mode control: theory and application[M]. Washington, D.C: Taylor and Francis, 1998: 27-48.
[20] LI R, LI T, BU R. Active disturbance rejection with sliding mode control based course and path following for under actuated ships[J]. Mathematical Problems in Engineering, 2013(1): 1-9.
[21] SUN Z, GE S. Switched linear systems: control and design[M]. New York: Springer, 2005: 45-62.
[22] BLANCHINI F, CASAGRANDE D, MIANI S. Modal and transition dwell time computation in switching systems: A set-theoretic approach[J]. Automatica, 2010, 46(9): 1477-1482.
Slidingmodecontrolbasedmultivariablelimitmanagementforaircraftengine
DUXian,GUOYingqing*,SUNHao,XUQingshi
SchoolofPowerandEnergy,NorthwesternPolytechnicalUniversity,Xi’an710072,China
Toovercometheshortcomingsoftraditionalmin-maxswitchinglogicwithlinearregulatorsforlimitmanagement,animprovedmethodisutilizedtosubstitutealllinearregulatorswithnonlinearslidingmoderegulators.Basedonthisimprovedapproach,amulti-inputcontrolstrategy,alongwithanewinnovativeswitchinglogicandamultivariableslidingmoderegulatorasthemaincontroller,isproposedtoremovetheconservatismofthetraditionalmin-maxapproachandtotakeadvantageofalltheactuatorsforenhancedperformance.Thesteady-stateworkingregulatorsunderthenewswitchinglogicareanalyzed,andnecessaryandsufficientconditionsareestablishedtoensurethatthemainregulatorisactiveforaccuratetrackingatsteadystate.Simulationresultsshowthattheproposedmulti-inputstrategyissuperiortotheimprovedsingle-inputslidingmodecontrollerinmin-maxstructure.Thenewmethodownstheabilitytoachievethetrackingtaskundermoretightconstraints,thesettlingtimeofthepossibilityofpursingfasterresponseisshortenedfrom1.91sto1.54s,andthefuelconsumptionatsteadystateisloweredforthesamecontrolobjectives.
turbofanengines;limitmanagement;min-maxswitchinglogic;slidingmodecontrol;multivariablecontrol
2016-01-08;Revised2016-02-22;Accepted2016-04-08;Publishedonline2016-04-131600
2016-01-08;退修日期2016-02-22;录用日期2016-04-08; < class="emphasis_bold">网络出版时间
时间:2016-04-131600
www.cnki.net/kcms/detail/11.1929.V.20160413.1600.006.html
*
.Tel.:029-88431121E-mailyqguo@nwpu.edu.cn
杜宪, 郭迎清, 孙浩, 等. 基于滑模控制的航空发动机多变量约束管理J. 航空学报,2016,37(12):3657-3667.DUX,GUOYQ,SUNH,etal.SlidingmodecontrolbasedmultivariablelimitmanagementforaircraftengineJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3657-3667.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0118
V233.7
A
1000-6893(2016)12-3657-11
杜宪女, 博士研究生。主要研究方向: 航空发动机限制管理, 模型预测控制及滑模控制。E-mail: mydx@mail.nwpu.edu.cn
郭迎清男, 博士, 教授, 博士生导师。主要研究方向: 航空发动机控制与健康管理。Tel.: 029-88431121E-mail: yqguo@nwpu.edu.cn
孙浩男, 博士研究生。主要研究方向: 发动机健康管理。E-mail: sunhao2013@mail.nwpu.edu.cn
徐清诗女, 硕士研究生。主要研究方向: 航空发动机延寿控制。E-mail: xqs@mail.nwpu.edu.cn
URL:www.cnki.net/kcms/detail/11.1929.V.20160413.1600.006.html
*Correspondingauthor.Tel.:029-88431121E-mailyqguo@nwpu.edu.cn
