一道不适合小学生做的数学题
2016-11-17江苏省如东县双甸镇双甸小学
江苏省如东县双甸镇双甸小学 袁 旭
一道不适合小学生做的数学题
江苏省如东县双甸镇双甸小学袁旭
有一次,班上两名同学为一道题争论不下,拿来让我评判,题目是这样的:“有甲、乙、丙三只布熊,A、B两种墨镜。现在给每个布熊配一副墨镜,有()种不同的选配方法。”
粗一看,以为就是用学生刚学的“搭配规律”来算,先选布熊,有3种可能,再选墨镜,有2种可能,3×2=6(种),如果这样做,那就大错特错了!那么正确的答案又是什么呢?我们先来剖析一下。
一、本题与教材例题很相似,但题目要求却不同
为了弄清错误的根源,我们先将原苏教版教材小学数学四年级下册“找规律”的例题与本题比较一下,看看有何异同(例题如下图):
通过比较不难发现:例题中小明要的只是一个木偶和一顶帽子!也就是说一共5件商品,我们只要考虑小明选中的2件商品的搭配情况,而不要考虑所有木偶都配上帽子是什么情况。小明一旦选择了一种木偶与一种帽子,那么就不需要考虑剩下的木偶与帽子如何搭配了。
但是本题就不同了,要求是“给每个布熊配一副墨镜”,也就是说任何一个布熊都要配墨镜,这就需要将所有布熊作为一个整体来考虑。对于这样一个整体而言,其中任何一个布熊所配墨镜变化了,这个整体的情况也就不一样了,哪怕还有两只布熊还没有变化。比如,可见,虽然甲、乙这两只布熊所配墨镜没有变化,只是丙的墨镜变了,但对于三只布熊这个整体而言已经属于两种不同的选配方法了。
因此,题目的要求不同,解题的方法也就不同。

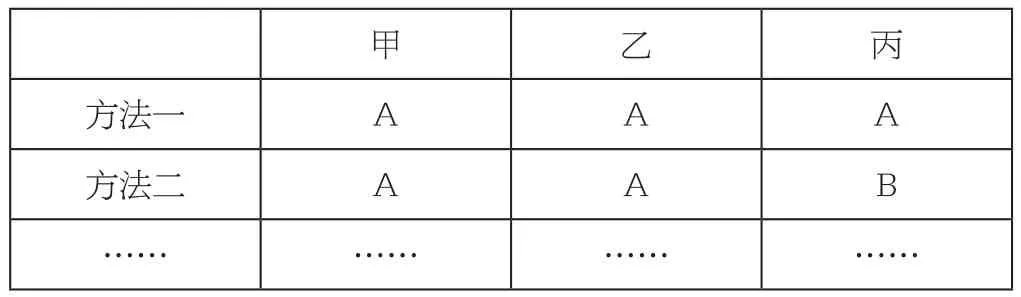
甲乙丙方法一 A A A方法二 A A B…… …… …… ……
二、2种不同的解题方法
1.例题的解法
解法一:先选木偶解法二:先选帽子

木偶 帽子黄花黑紫花黑绿花黑
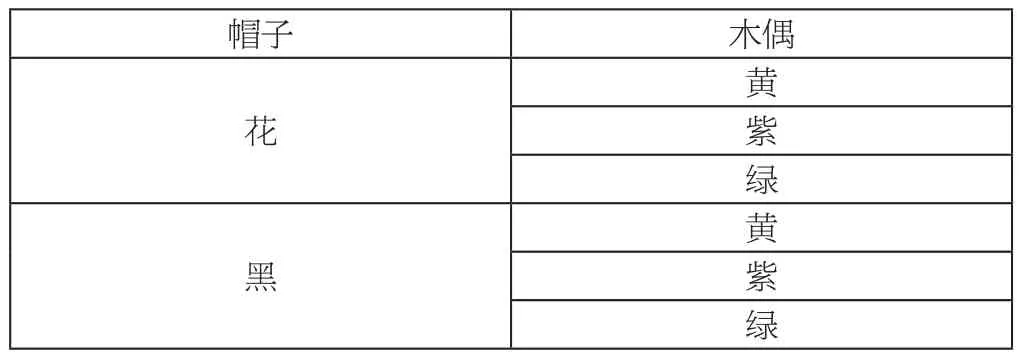
帽子 木偶花黄紫绿黑黄紫绿
这里无论是先选什么,都是用木偶数与帽子数相乘,即用“3×2=6种”来解答。
如果用字母a表示木偶数(或种类数),b表示帽子数(或种类数),买其中一个木偶与一顶帽子就可以:a×b。
2.本题的解法
由于要给每个布熊配墨镜,因此要考虑整体情况,列举如下表:

甲乙丙方法一 A A A方法二 A A B方法三 A B A方法四 A B B方法五 B A A方法六 B A B方法七 B B A方法八 B B B
由于每个布熊都有两种选择,写成算式就是:2×2×2=8(种),即23。如果用a表示墨镜数(种类数),b表示布熊数(个数),那么分别配墨镜的不同情况就是a的b次方:ab。
3.“2个”与“2种”的区别不影响解题方法
如果将例题的帽子数“2个”改为“2种”,哪怕将木偶数也增加,“3个”木偶变为“3种”木偶(如下图所示),这样木偶与帽子数都变多了,那么“买一个木偶娃娃,再配一顶帽子”,会有多少种选配方法呢?

很显然,尽管帽子数与木偶数都增加了,但由于种类并没有增加,所以小明选出来的这“一个”木偶,仍然是“黄、紫、绿”3种可能中的一种,选“一顶”帽子,也同样只有2种可能,解法依然是“3×2 =6种”,即种类数与种类数相乘。
但是如果换要求,变成:“给每个木偶娃娃配一顶帽子,有多少种选配方法?”那就是第二种解法了(假设木偶是9个):29=512(种)
可见,从两种商品中各选一个,是比较适合小学生学习的,解法就一种;而像要求二这种问题,解法多样,晦涩难懂,根本就不适合小学生学习!
综上所述,我们在平时的教学中,必须要贴近教材。不要任意拔高要求,像本文所提到的这种给布熊配墨镜的题目与教材的例题解法根本不一致,如果出题者还沾沾自喜地认为是教材例题的迁移,那就悲哀了!
