巧妙迁移提升数学学科素养

江苏省南京市浦口区大桥中学　丁　峰

巧妙迁移提升数学学科素养

江苏省南京市浦口区大桥中学丁峰

本文通过一道习题，提出教师要充分信任和尊重学生，并指导学生如何发现问题、探究问题、解决问题，让教师的“教”服务于学生的“学”，让学生拥有一份属于自己的发展空间和时间，去动手、去观察、去体验、去思考、去发现，激发他们学习的积极性和主动性，培养他们的创新能力。

自主探究；巧妙迁移；创新思维

现代课堂教学的基本理念是以学生为主体，就是要在课堂上给学生创造自主探究学习的机会，让他们充分拥有自由思考的时间和空间。这对于他们自身能力的培养、研究意识的形成都是十分必要的。这一理念对于我们教师来说人人皆知，但却常常不能落实在行动上。究其原因主要有两个：一是教师心里没底，难于控制学生的学习过程；二是担心影响教学进度、打破教学计划。事实上这是旧的观念还没有转变。

课程标准明确指出：有效的数学学习活动不能单纯地依赖模仿与记忆，应积极动手实践、自主探索与合作交流。教师应激发学生的学习积极性，充分提供从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的知识与技能、思想和方法，获得广泛的数学活动经验。应坚守“学生是学习的主人，教师是学习的组织者、引导者与合作者”。

在复习勾股定理时，一位同学巧妙的解题使我和学生得到了意外的收获。本文真实记录了这一节课的重要片断。

一、过程（反馈练习部分）

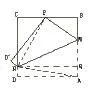
如图，在边长为12cm的正方形纸片ABCD中，点P在边BC上，已知PB=5cm。如果将纸折起，使点A落在点P上，试求折痕MN的长。

我让学生先分组讨论，几分钟后有的组要求发言：

学生1：只需过N点作NQ⊥AB，垂足为Q，NQ=12cm，

求出MQ的长，再用勾股定理计算出MN的长。

该同学上黑板书写计算过程：

过N点作NQ⊥AB，垂足为Q，则NQ=12cm，

由折叠知MA=PM，设MA=x，则PM=x，MB=12-x，

连接PN、AN，同理PN=AN，设DN=y，则CN=12-y，

在Rt△CNP与Rt△AND中，

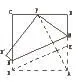
学生2要求发言：如图，连接PA，在Rt△PAB中，根据勾股定理计算：，过点D作DE∥MN，由△PAB与△EDA全等及平行四边形对边相

等的性质得MN=DE=AP=13。

该同学上黑板书写计算过程：

又∵∠B=∠EAD，DA=BA，

∴△PAB≌△EDA（ASA），

∴DE=AP，

∵在四边形NDEM中，DE∥MN，DN∥ME，

∴四边形NDEM是平行四边形，

∴MN=DE，

∴MN=DE=AP=13。

全班一片掌声！非常漂亮。

此时，我立刻想到他运用了正方形中的一个结论。

我又稍作点评：正方形中的一个结论你们是否还有印象，该同学能把正方形中证明的结论用在勾股定理的计算中，使得三次勾股定理的复杂计算变得非常简洁，非常棒！我们在学习过程中要不断总结方法和将知识迁移。

二、反思

本节课，由于该同学精彩的解题，虽然没有完成预定的反馈练习，但是学生对解题的方法和能力得到了有效的训练，更重要的是学生在自主探究、合作学习的过程中充分享受了成功的喜悦，学习数学的积极性被充分调动了起来，真正做到举一反三，创新思维也得到了一次有效的锻炼，而且我和学生都受益匪浅。这道题的整个探究过程充分反映了学生蕴藏着无限的创新能力。作为教师要充分信任和尊重学生，建立平等的师生关系，一心一意地让教师的“教”围绕学生的“学”而服务，让学生拥有一份属于自己的发展空间和时间，去动手、观察、体验、思考、发现、发挥他们的最大潜能，这样就能激发他们学习的积极性和主动性，培养他们的创新能力。试想，如果我按常规方法去分析讲解，没有放手引导学生合作探索解决相关问题，就不会有课堂上的创新和激情。

这节课也表明：学生只有在教师充分放手的情境中学习，才能学得积极、主动、充满乐趣，才能把求知的课堂变成他们思考、探索和创新的天地。

三、结论

尊重与承认经验是学生学习的重要资源，可以有效地帮助教师改变自己的教学方式和教育观念，从而实现学生学习方式的根本转变。给孩子一个自由的空间，让他们自己去观察，发现问题，活动中进行小组合作，鼓励他们交流，培养他们的语言表达能力，整个过程强调了学习方法、思想方法和学习态度的培养，注重学生自己动手、动脑和发现。这不仅培养了学生的动手能力，使学生增进知识，更重要的是使学生学会了寻找解决问题的策略和方法，同时也培养了他们实践能力和创新精神。