一种数据特征敏感的高效数据聚集编码方案

解 锋，叶晓慧

(1.海军工程大学 电子工程学院，武汉 430033；2.海军工程大学 科研部，武汉 430033)



一种数据特征敏感的高效数据聚集编码方案

解 锋1，叶晓慧2

(1.海军工程大学 电子工程学院，武汉 430033；2.海军工程大学 科研部，武汉 430033)

物联网中数据聚集算法设计面临的主要困难是：数据聚集时数据冗余的发现和消除，数据特征的发现均需要周密的思考，数据聚集时通信效率的提升通常需要较高超的数据编码技巧，精巧的算法设计思路；因此，研究数据聚集的高效率编码算法对于降低数据聚集的能耗具有重要的意义；当前研究中对于数据聚集中编码的综合讨论尚不充分，论文首先对问题进行建模，提出数据平滑泛型的概念，并通过分析得到数据平滑泛型将显著提高通信效率提升指数，在此基础上，论文提出了一套数据特征敏感的物联网高效数据聚集编码方案，包括数据聚集前的数据特征敏感的编码方法，基于CRT的数据编码准备方法，以及多节点数据聚集的可聚集变换方法；所给出的方法均经过严格的理论分析和证明论证，表明了方案的可行性。

数据聚集；编码算法；高效率；通信效率

0 引言

物联网在舰船设备状态监测和数据采集方面有重要的应用。在基于物联网中数据采集中，物联网感知节点获取或者产生的感知信息通常需要传递到中央节点，这一过程称为数据聚集。由于物联网中多数节点(例如传感器感知节点，以及中间传输节点)是能耗敏感的，因此，在设计数据聚集算法时需要首先考虑算法的通信能耗和计算能耗[1-3]。通信能耗和计算能耗较少的数据聚集算法将使得数据采集更加高效和可靠。

因为通信能耗通常比计算能耗要高一个数量级，因此降低通信能耗成为首要考虑因素。提高数据聚集效率的一个基本方法就是设法减少通信中数据传输的字节数，从而减少数据传输的能量消耗。目前对于数据聚集编码效率的研究工作并不多见[4-5]，尤其是对于聚集节点在数据聚集后的高效传输问题研究较少[6-10]。因此，我们认为可以从两个方面来研究和提出高效率的数据聚集算法，一个是数据聚集时的单节点高效率数据传输方法，主要是从感知节点到聚集节点的高效数据传输数据编码方案，另一个是数据聚集时的多节点数据优化汇聚方法，主要是多感知节点到聚集节点进行数据汇聚后，聚集节点高效率地进行数据传输的数据编码方案。

数据聚集算法设计面临的主要困难是：数据聚集时数据冗余的发现和消除，数据编码的数据压缩效率和编码算法本身的能耗，都是需要考虑的因素。本文讨论如何利用数据的特征进行编码从而提高数据聚集的效率，提出一种高效数据聚集算法，其创新性在于：给出一个数据聚集的正则方法模型，用于数据聚集的基本方法建模；提出一套数据聚集算法，该算法可以提高数据传输的效率；给出完整的算法理论性能分析。

1 问题建模

不失一般性，首先对所研究问题进行建模，便于后续的算法设计，同时有利于算法应用的通用性。

研究中主要考虑的对象为感知数据及其编码，另外就是编码数据进行汇聚后的数据。

定义1:感知数据。感知的原始数据，表示为SDATA。

定义2:编码数据。编码后的数据，表示为CDATA。

定义3:编码函数。该函数的输入为SDATA，输出为CDATA，函数表示为COD。

定义4:聚集数据。编码数据的函数计算结果。表示为ADATA。

定义5:聚集函数。函数输入为CDATA，输出为ADATA，函数表示为FUN。

图1给出了数据聚集中主要算法和数据的模型。

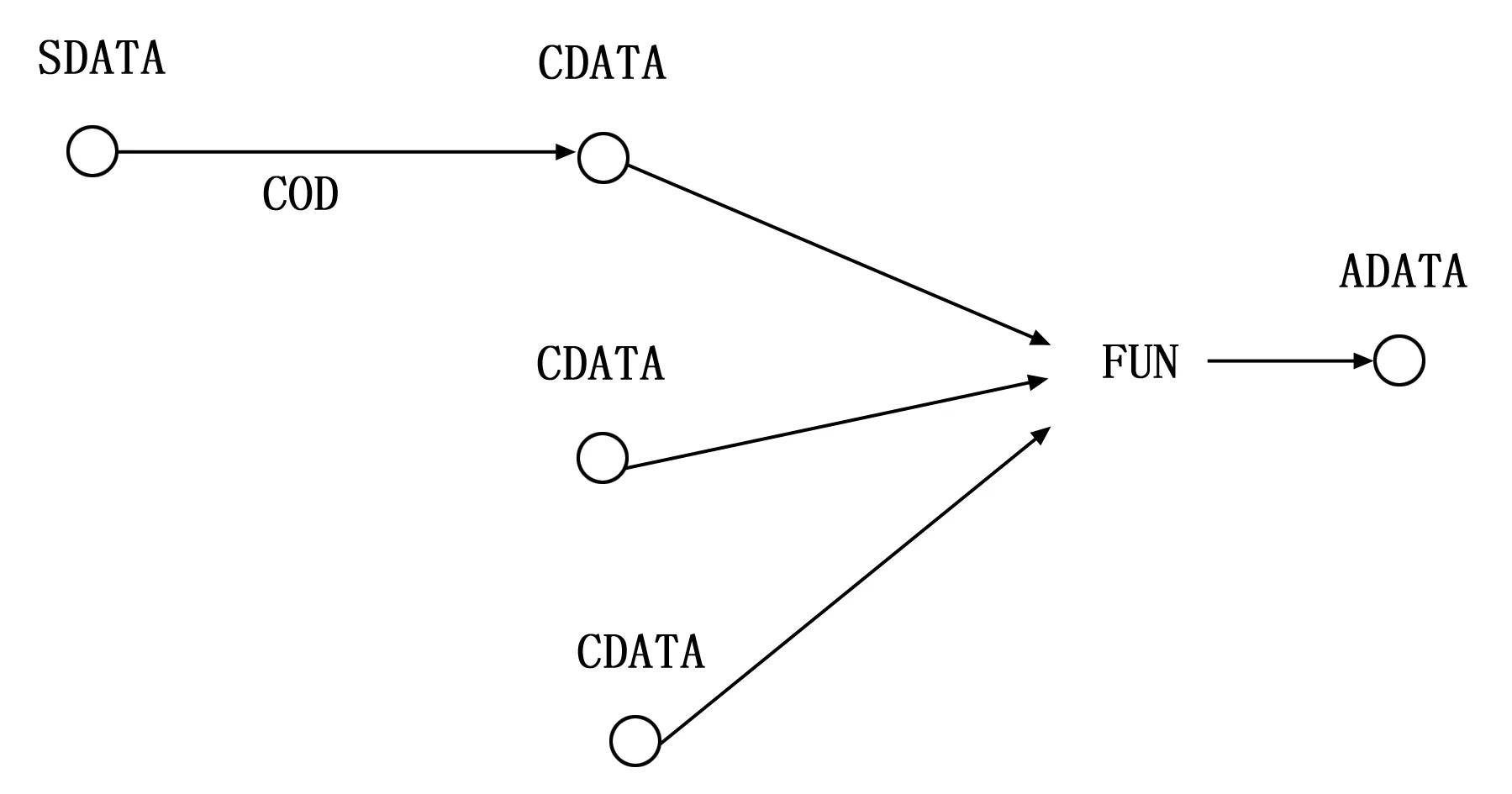
图1 数据聚集的算法和数据模型

首先考虑最简单的情形：假设聚集节点和感知节点之间为单跳(single-hop)。对于这种情形，数据聚集的通信代价主要由单跳节点之间的通信代价组成，因此问题可以转换为：如何寻找合适的COD，以减少单跳节点间的通信代价。解决这一问题的思路自然是：寻找一种高效率的变换，使得聚集数据变短。因为，较短的聚集数据将占用较短的通信时间，从而提高了通信效率。

2 数据特征敏感的数据编码方法

通常，感知数据具有一定的特征，其原因在于感知数据通常来自单一传感器节点，而传感器节点的感知数据的范围通常是有限的，同时，由于感知的环境参数(例如，温度，湿度等)在通常情况下不会出现大范围的波动，因此，这为感知数据的编码带来了可能。

感知数据的传递能耗是数据聚集算法设计的主要考虑因素，因此，为了使得传输的感知数据变短，我们提出数据特征敏感的数据编码方法。下面首先对数据特征进行建模：

定义6:数据平滑范型(data smooth form，DSF)。一种表征数据平滑程度的特征。不失一般性，假定需要传输的数据为，DSF表征了数据变化、数据组成、数据值范围等特征。

下面给出若干DSF，通常DSF是开放的，可以进一步扩充，这一思路的好处是后续方案设计也是开放的，具有可扩充性。

1)DSF1：数据变化平滑范型。即：

|Di-Di-1|<Δ1，(i=2,..,n)

(1)

这里Δ1表示一个非负值，表征了数据之间的差异程度。

2)DSF2：数据值平滑范型。即：

|Di-AVG|<Δ2，(i=1,..,n)

(2)

这里Δ2表示一个非负值，表征了数据与参照系AVG之间的差异程度。

3)DSF3：数据枚举平滑范型。即：

Di∈SET，(i=1,..,n)

(3)

这里SET表示一个数值枚举集合，该集合的最小闭包元素的个数表征了枚举的数量。

容易看到，如果待聚集的感知数据满足DSF，则在数据传递之前可以采取如下编码策略以减少数据长度，从而减少数据通信代价。这里分别针对上述3种DSF给出编码策略如下，后面再给出对这些策略的性能分析。

1)针对DSF1。采取策略POLYCE-DSF1，即只上传变化值。

发送端上传数据为：

[D1],

[D2-D1],

[D3-D2],

⋮

[Dn-Dn-1].

这里每一行表示一次数据上传，[*]表示上传的感知数据。

接收端恢复数据的方法为：

D1，

D2 <= D1+[D2-D1]

⋮

Dn <= Dn-1+[Dn-Dn-1]

2)针对DSF2。采取策略POLYCE-DSF2，即差值上传法。

发送端上传数据为：

[AVG], [D1-AVG],

[D2-AVG],

[D3-AVG],

⋮

[Dn-AVG].

这里每一行表示一次上传。

接收端恢复数据的方法为：

AVG, D1<=AVG+[D1-AVG]

D2 <= AVG+[D2-AVG]

⋮

Dn <= AVG+[Dn-AVG]

3)针对DSF3。采取策略POLYCE-DSF3，枚举值上传法。

发送端上传数据为：

[ENU1],

[ENU2],

⋮

[ENUn]

这里每一行表示一次上传。

接收端恢复数据的方法为：

DATA[ENU1]

DATA[ENU2]

⋮

DATA[ENUn]

这里DATA表示原始感知数据集，ENUi表示原数据在原始集合中的枚举位置。

注记：

1)在实现时，通常在第一组数据上传时，添加策略编号。从而表示该上传方法使用的策略，接收端可以根据该策略编号确定如何进行数据恢复；

2)策略POLYCE-DSF3中DATA通常为事先约定的，也可以在第一个包中发送。

3)上述策略由发送端决定，发送端对数据是否满足DSF可以通过“自学习”机制完成。即通过对待发送数据的分析完成。

4)这种自学习机制使得发送端的策略不是固定的，可以根据待发送数据的特征进行相应改变。

性能分析：

在给出性能分析之前，先定义性能评价指标：

定义7： 通信效率提升指数(communicationefficiencyindex，CEI)。该指数度量了通信效率特升的程度。定义如下：

CEI=|ΔC/C0|

(4)

这里，C0表示原来的通信效率，ΔC表示通信性能的改进值。

不失一般性，我们简化CEI中的通信计算主要为传输数据的长度所决定，这主要是因为通常通信带宽是满足的情况下，传输时间主要由传输数据的长度所决定。另外，在数据计算方面可能会导致一些延迟，但是由于数据计算十分简单，因此这部分延迟可以忽略不计。

定理1:如果SDATA满足DSF1到一定程度，则策略POLICY-DSF1的CEI≥90%。

证明：假设D1的长度为|D1|，由于|Di-Di-1|<Δ1，(i=2,..,n)，传输数据长度的上界为|D1|+(n-1)|Δ1|，原始数据长度为∑|Di|，约为n|D1|，于是

CEI= 1- (|D1|+(n-1)|Δ1|)/(n|D1|)

(5)

简单变形和整理

CEI = 1-(1+(n-1) |Δ1|/|D1|)/n =

(n-1)/n(1- |Δ1|/|D1|)

(6)

如果|Δ1|/|D1|≤1/10，n足够大，(n-1)/n≈1，则

CEI ≥ 90%

因此，如果DSF1满足一定程度，则策略的CEF≥ 90%。

定理2:如果DSF2满足一定程度，策略POLICY-DSF2的CEI≥90%。

证明：假设AVG的长度为|AVG|，由于|Di-AVG|<Δ2，(i=1,..,n)，则传输数据长度的上界为|AVG|+n|Δ2|，原始数据长度为∑|Di|，假设约为n|D1|，于是

CEI = 1- (|AVG|+n|Δ2|)/(n|D1|)

(7)

简化|AVG|/|D1|≈1,则

CEI=1-1/n-|Δ2|/|D1|

(8)

如果n足够大，忽略1/n，简化为：

CEI ≈ 1-|Δ2|/|D1|

(9)

如果|Δ2|/|D1|≤1/10，则

CEI ≥ 0.9

因此，如果DSF2满足一定程度，则策略的CEF≥ 90%。

定理3:如果DSF2满足一定程度，策略POLICY-DSF1的CEI≥90%。

证明：假设ENU的长度为|ENU|，易知，ENU的长度有集合SET的元素个数决定，即|ENU|≤log2‖SET‖，这里‖*‖表示集合*的元素个数。传输数据长度的上界为nlog2|SET|，原始数据长度为∑|Di|，假设约为n|D1|，于是

CEI = 1- (nlog2‖SET‖)/(n|D1|)=

1- log2‖SET‖/|D1|

(10)

如果log2‖SET‖/|D1|≤1/10，则

CEI ≥ 0.9

因此，如果DSF3满足一定程度，则策略的CEF≥ 90%。

由定理1～3，可以得到：

推论1 满足POLICY-DSFi(i=1,2,3)策略的CEI≥90%。

证明：由定理1，定理2，定理3可知。

3 基于CRT变换的数据编码准备

上节给出了满足DSF条件的数据的编码方法，下面的研究问题是，如何使得要SDATA满足数据平滑范型DSF。如果感知数据SDATA天然满足DSF，即可以直接采取上节的编码方式进行数据传递。如果感知数据SDATA不能天然满足DSF，虽然这种情况的概率可能较小，仍然可以采取CRT变换将感知数据SDATA变换成满足DSF的数据。

定义8:CRT变换。将数据D变换成一组数据，这一组数据是D关于一组剩余类基的剩余。这里n作为系统参数，在实现中视实际情况而定。

定义9:剩余类基RBase。剩余类基RBase为一组互素的素数。

定理4:CRT变换为等价变换。

证明：证明是容易的。可以从经典数论书中得到。这里给出概要：

由于

D ≡ d1 (modR1)

D ≡ d2 (modR2)

⋮

D ≡ dn (modRn)

可知，D关于剩余类基RBase=的CRT变换结果为。下面需要证明，在给定剩余类基的情况下，D和是等价的。

所谓等价是指：

1)给定RBase=和D，计算，有且仅有一组；

2)给定和RBase=，求D，有且仅有一个。

根据CRT的性质(可见经典数论相关书籍)，上述要求(1)，(2)可以满足。于是，等价性满足。

定理5:CRT变换使得SDATA更容易满足DSF。

证明：SDATA经过CRT变换后，得到一组，如果适当的选取剩余类基RBase，可以使得具有较高概率满足DSF。

举例：

假定剩余类基RBase为<3,5,7>，则d1具有较高概率满足DSF1，d2具有较高概率满足DSF2，d3具有较高概率满足DSF3。因此，非常容易满足DSF。

下面，我们提出基于CRT变换方法的数据聚集过程如下：

1)在上传方生成一组CRT剩余类基RBase，发送给接收方；

2)上传方将待上传数据D通过CRT变换为一组；

3)分别对di(i=1,2,..,n)进行DSF编码策略，然后上传给接收方；

4)接收方恢复每一组di()，利用CRT的剩余基RBase恢复出D。

一般性讨论：

上述讨论中主要针对单跳情形，即感知节点和聚集节点之间为单跳(Hop)的情形，对非单跳的情形，仍然可以采用上述的编码方案。主要原因如下：多跳情形下，相当于增加了中间节点，中间节点只起到转发的作用，因此，如果采取上述编码方案，其CEI保持不变。将这一结论通过如下定理来表述：

定理6: 在多跳情形下，若单跳CEI=t，则多跳CEI=t。

证明：若每一跳通信效率提升将为t，令原单跳通信代价为C，则单跳实际通信代价为(1-t)C。若跳数为n(即中间节点为n-1)，则原通信代价为C*n；改进后通信代价为(1-t)C*n，于是CEI=1-(1-t)C*n/(C*n)=t。

4 多节点数据聚集的可聚集变换方法

上一节重点研究了数据聚集时单个感知节点数据编码的方法，下面讨论数据聚集时具有多个感知节点数据需要聚集的编码方法。

在CRT变换后，将SDATA变换成具有DSF特征的CDATA。假设待聚集的数据为CDATA1，CDATA2，…，CDATAn。

下面我们说明，待聚集数据不需要将CDATA解码成SDATA就可以完成数据的聚集运算。

定义10: 如果编码方案可以不需要解码，直接计算出数据聚集的结果，则称该编码变换为可以聚集的变换。

定理7:CRT变换是可以聚集的变换。

证明：CDATAi(i=1,…,n)是基于相同的RBase，假设RBase中剩余类个数为m，CDATAi对应的剩余为Di=，(i=1,…,n)。假设数据聚集运算为加法，则令

D1 ≡ ∑di1 (modR1)

D2 ≡ ∑di2 (modR2)

⋮

Dm ≡ ∑dim (modRm)

由，以及剩余类基RBase=，可以计算出D，D等于为∑CDATAi的结果。因此，CRT变换是可以聚集的变换。

5 多节点数据聚集的条件聚集变换方法

前述部分重点研究了数据聚集前的编码算法，下面讨论数据聚集后使得聚集后数据满足一定数据条件从而提高数据传输效率的编码算法。

定义11: 被聚集数据(Pre-AggregateData，PreAD)。包括感知的数据，这些数据将被发送到聚集节点进行数据聚集。

定义12: 聚集后数据(post-aggregatedata，PostAD)。聚集节点将被聚集数据进行聚集后产生的数据。

定义13: 满足条件C的聚集变换AC-C(AggregationConversionwithConditionC)。将被聚集数据进行变换，使得PostAD可以恢复出PreAD，且PostAD满足条件C。

容易看到，AC-C的输入是PreAD，输出是PostAD，且PostAD可以恢复出PreAD，同时PostAD满足一定的条件C。

假设PreAD由[A1，A2，…，An]组成，PostAD由[B1，B2，…，Bn]组成，可以考虑的条件C通常包括：

C1：[B1，B2，…，Bn]满足DSF1；

C2：[B1，B2，…，Bn]满足DSF2；

C3：[B1，B2，…，Bn]满足DSF3；

为便于理解应用场景，下面给出相关节点的定义：

定义14: 被聚集节点。发送PreAD的节点，通常是多个节点。

定义15: 聚集节点。发送PostAD的节点。

定义16: 接收节点。接收PostAD的节点。

容易看到，如果PostAD满足C1，则在发送PostAD的时候将较大的减少发送的包长度。换句话说，在发送PostAD的时候，将只需要发送较少的数据，然后在接收端通过这些较少的数据恢复出PostAD，然后在从PostAD恢复出PreAD。

定理8:AC-C1将提高传输效率约为1-(‖B1‖+(n-1)‖Δ1‖)/∑‖Ai‖；

证明：PreAD由[A1，A2，…，An]组成，如果不进行聚集，则这些数据从聚集节点发送给接收节点时需要发送的长度为∑‖Ai‖。如果进行了AC-C1，则发送的是PostAD=[B1，B2，…，Bn]的DSF编码，即类似与[B1，C1，C2，C3，…,Cn-1]，由于Ci(i=1,…,n-1)<Δ1，因此，从聚集节点发送到接收节点需要发送的长度为‖B1‖+(n-1)‖Δ1‖。

定理9:AC-C3将提高传输效率约为1-(‖AVG‖+n‖Δ2‖)/∑‖Ai‖；

证明：PreAD由[A1，A2，…，An]组成，如果不进行汇聚，则这些数据从汇聚节点发送给接收节点时需要发送的长度为∑‖Ai‖。如果进行了AC-C3，则发送的是PostAD=[B1，B2，…，Bn]的DSF编码，即类似与[AVG，D1，D2，D3，…, Dn]，由于Di(i=1,…,n)<Δ2，因此，汇聚编号从汇聚节点发送到接收节点需要发送的长度为‖AVG‖+n‖Δ2‖。

5 结束语

本文采取严格的理论论证的方法，提出了一套物联网数据聚集中的高效率数据编码算法，通过利用数据特征进行编码，使得编码后的聚集数据长度减少，同时，利用CRT变换，可以进行编码前的准备工作，且CRT变换是可以聚集的变换，另外，还提出了数据聚集后的使得聚集数据满足高效率数据传输条件的变换方法。这些编码方法的可行性均经过严格的论证。所提出的方法能够提高数据聚集的通信效率，减少数据传输的能耗，对物联网数据聚集的高效率完成具有重要的意义。

[1]王 培. 无线传感器网络延迟优化的数据聚集问题研究[D].合肥：中国科学技术大学,2010.

[2]李 娜. 无线传感器网络的网内数据聚集关键技术研究[D].北京：北京邮电大学,2011.

[3]朱珺青,郭龙江,任美睿,等. 基于组移动模型的移动传感网数据聚集算法的研究[J]. 计算机研究与发展,2011(S2):231-235.

[4]范文彬,郭龙江,李金宝,等.MPMC:一种无线传感器网络多信道多功率数据聚集调度算法[J]. 计算机研究与发展,2012(7):1568-1578.

[5]蒋文涛,吕俊伟,杨曙辉,等. 传感器网络中面向数据聚集的有向分簇算法[J]. 北京邮电大学学报,2012(3):25-29.

[6]吴 旦,王改云,李小龙. 基于最小覆盖集的WSN数据聚集算法[J]. 计算机工程,2012(2):97-99.

[7]于 博. 无线传感器网络数据聚集调度技术的研究[D].哈尔滨：哈尔滨工业大学,2013.

[8]王涛春,秦小麟,刘 亮,等. 无线传感器网络中安全高效的空间数据聚集算法[J]. 软件学报,2014(8):1671-1684.

[9]李金宝,王 蒙,郭龙江.MR-MC无线传感器网络最小延迟数据聚集调度研究[J]. 通信学报,2014(10):192-199.

[10]冯 诚, 李治军,姜守旭. 无线移动感知网络上的数据聚集传输规划[J]. 计算机学报,2015(3)：685-700.

A Data Context-aware High Efficient Data Aggregation Scheme

Xie Feng1，Ye Xiaohui2

(1. Electronics Eng. College, Naval Univ. of Engineering, Wuhan 430033, China；2. Office of R & D，Naval Univ. of Engineering, Wuhan 430033,China)

The main difficulty of data aggregation algorithm design in the Internet of things is the discovery and elimination of redundant data, and the discovery of data characteristics need to be careful. The improvement of communication efficiency in data aggregation is usually required to be more skillful than the encoding technique, and the design of sophisticated algorithm. So the high efficiency of coding algorithm for data aggregation in Internet of Things is of great importance for energy cost in data aggregation. In current researches, the integrated coding method for data aggregation has not been explored thoroughly. Firstly, the problem is modeled, and the concept of data smoothing is proposed, and the data smoothing generic will significantly improve the communication efficiency. On this basis, The paper proposes a data context-aware coding scheme for data aggregation. It includes coding method before data aggregation, CRT-based data coding preparation method, multiple data aggregation transformation that can be aggregative. The methods are justified by rigorous theoretic analysis, which proves its applicability.

data aggregation; coding algorithm; high efficiency; communication efficiency

2015-09-07；

2015-10-26。

国防预研基金(9140A27020113JB11393)。

解 锋(1979-)，男，山东济南人，博士生，主要从事通信技术方向的研究。

叶晓慧(1962-)，男，湖北武汉人，博士生导师，教授，主要从事通信技术方向的研究。

1671-4598(2016)03-0179-04

10.16526/j.cnki.11-4762/tp.2016.03.048

TN915.0

A