基于改进蚁群算法的无人机动态航路规划

林 娜，刘二超

(沈阳航空航天大学 计算机学院，沈阳 110136)



基于改进蚁群算法的无人机动态航路规划

林 娜，刘二超

(沈阳航空航天大学 计算机学院，沈阳 110136)

研究无人机航路规划，针对基本蚁群算法易于陷入局部最优、规划航路耗时长的问题，对基本蚁群算法进行了改进；引入航路点的动态自适应选择策略和信息素挥发因子动态自适应调整准则，有效克服了基本蚁群算法的不足，并对规划出的航路进行了平滑处理，使其更加满足无人机实际飞行需求；通过仿真分别规划出无人机在静态威胁和动态威胁中的航迹，仿真结果表明，与基本蚁群算法和遗传算法相比，改进的蚁群算法在两种飞行环境中均能规划出较优的航路。

无人机；蚁群算法；选择策略；信息素；平滑处理

0 引言

无人机(unmanned aerial vehicle, UAV)在现代战争中的使用越来越广泛，这与无人机自身独有的零伤亡、体积小、成本低、机动性好以及对作战环境要求低等特点密不可分。无人机航路规划(UAV Route Planning)是无人机实现自主导航飞行的核心技术，它是在一个具有动态威胁的环境中，依据地形和敌方情报，在预定任务、威胁分布、燃油限制等约束条件下，于出发点和终点之间找到一条可飞航迹。

文献[1]提出了一种基于A*算法的无人机航路实时规划算法，然而A*算法计算量较大，因此对机载处理系统的性能要求较高。文献[2]提出了一种改进概率地图法的算法，作者只把最短航迹作为唯一的优化目标，考虑因素较为单一。文献[3]使用蚁群优化算法对UAV进行航路规划，但是作者只是针对室内环境进行试验，而且规划航迹呈折线状，无法满足无人机实际飞行需求。文献[4]采用快速探索树(rapidly exploring random tree, RRT)规划算法提高无人机在线搜索速度，但并没有考虑无人机自身的动力约束，无法满足飞行条件。文献[5]提出了基于Voronoi图的航路规划算法，该算法以已知的威胁为中心采用矢量法为无人机飞行空间建模时，当飞行空间复杂时存在较大的空间建模比较复杂。文献[6-7]提出了基于遗传算法的航路规划方法，遗传算法不受搜索空间的限制，不依赖梯度信息，在航路规划中应用较广，但是基本蚁群算法在求解复杂问题时会出现进化过程过早收敛的问题。

为了规划出满足无人机实际飞行的航路，本文设计了一种基于改进蚁群 (modified ant colony optimization, MACO)算法的无人机航路规划算法。首先，改进基本蚁群算法的状态转移规则同时对信息素挥发因子进行自适应调整。其次，结合已知的威胁信息采用MACO算法对无人机进行航路预规划，并对预规划出的航路进行平滑优化。最后，无人机按预规划航路飞行，飞行过程中使用机载雷达等探测设备对周围飞行环境进行探测，发现突发威胁时，对航路进行局部重规划，从而避开动态攻击。

1 航路规划问题

当无人机以恒定高度飞行处于巡航状态时，那么可以用二维平面等效其飞行区域。因此，研究无人机在二维平面下的航路规划是必要且有意义的。本文就以二维平面为无人机飞行空间，假定无人机以恒定速度飞行，并综合考虑各种威胁和约束，对无人机航路进行规划。

1.1 威胁表示和任务描述

为了明确表示出无人机的飞行航路，需要对无人机的飞行区域进行建模。假设无人机在大小为350 km×350 km的平面区域进行侦查作业。无人机在侦查过程中会遇到各种威胁，本文主要考虑敌方雷达，防空导弹阵地，地形威胁等约束条件。如图1所示是无人机飞行环境模型，在笛卡尔坐标系下，采用平面圆域(X,Y,R)等效各种威胁，圆心所在位置(X,Y)用以模拟威胁源出现的位置，圆的半径R用以模拟威胁源的有效威胁范围，各种威胁圆构成了无人机的危险飞行区(danger zones)或者禁飞区(no-fly zones)。

(1)

(2)

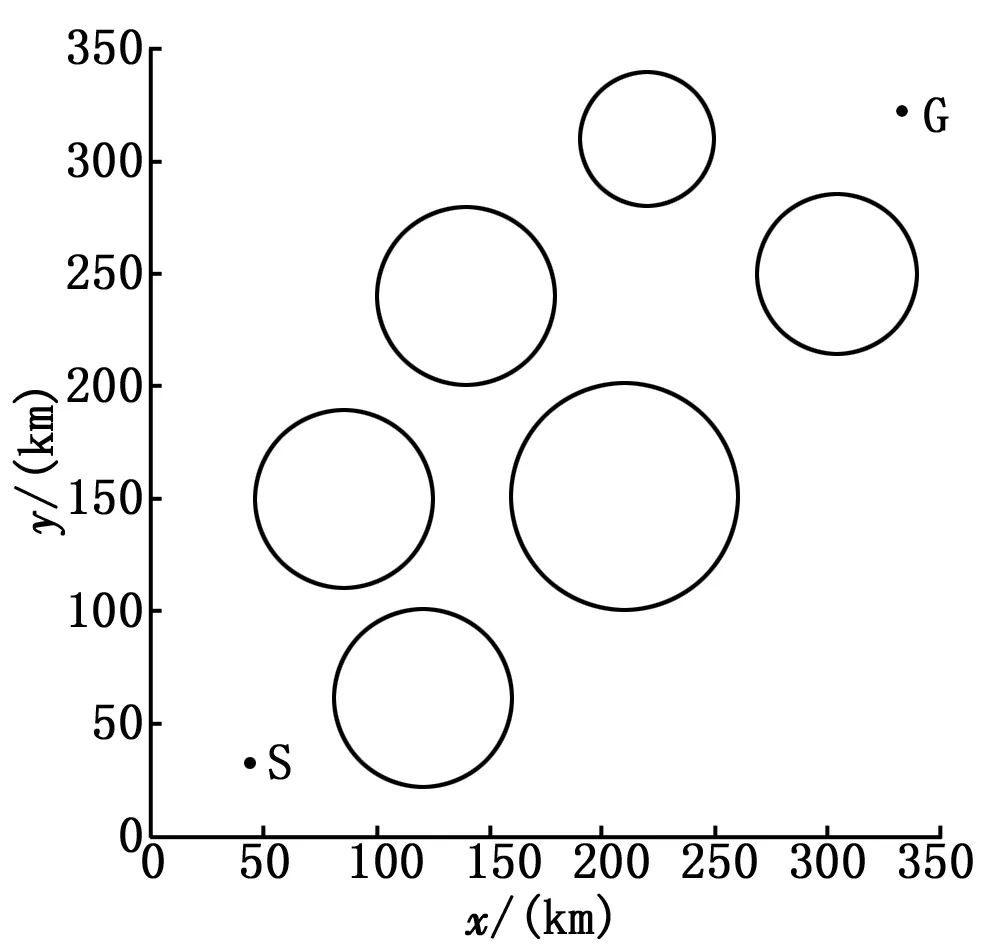
图1 无人机飞行环境

1.2 航路评价模型

无人机飞行航路的优劣程度直接影响UAV的作战能力，因此通过对无人机飞行区域进行建模得到航路节点后，仍需利用航路评价模型评估各段航路以及总体航路的性能。在考虑无人机飞行航距、受威胁影响程度和无人机拐角限制等因素的基础上，本文采用如下的评价模型来对无人机航路进行评估[8]：

(3)

式中，Fcost为无人机航路性能指标函数；ω1、ω2、ω3为权重系数，ω1、ω2、ω3∈[0,1]且有ω1+ω2+ω3=1，Clength惩罚飞行距离相对较长的航路，确保无人机飞行的飞行距离最短，从而降低其燃料消耗并减少飞行时间；Cturn惩罚存在较多拐角的航路，从无人机自身性能约束来讲，一条拐角较多的航路意味着无人机在飞行时经历的制动点多，频繁的制动将会增加无人机的飞行风险，本文第4部分还采用了平滑的办法对航路上的拐点进行平滑；Cthreat为第i段航路上的威胁代价，为了更加精确地表示某段航路上的威胁代价，将待评估的某段航路均分成N等分[1]，分别计算航路上的等分点到威胁的直线距离。如图2所示，在待评估的航路上找出均匀分布的5个点，分别计算各个点到威胁源的威胁代价，最后累加求和即为该段航路上的威胁代价：

(4)

式中，Kj为第j个威胁的强度，Rij为航路上的点与第j个威胁的距离，N为无人机的机载雷达在当前飞行位置下所能探测到的威胁的总数。

图2 威胁代价示意图

2 改进蚁群算法的航路规划

2.1 蚁群算法的基本原理

受到真实蚁群觅食行为的启发，M.Dorigo、V.Maniez-zo、A.Colorini等人于1991年首先提出了蚁群算法(Ant Algorithm),并应用在TSP问题的求解上，取得了较好的成效[9]。

蚁群算法是一种生物仿真进化算法，旨在解决路径规划过程中的组合优化问题。在蚁群算法中，一只蚂蚁在其觅食过程中会路径上释放生物信息素，后到的蚂蚁会感知到前者释放的信息素，同时后到者也会释放信息素从而强化已经存在的信息素，如此反复进行。因此，经过蚂蚁越多的路径信息素浓度越高，被后到蚂蚁选中的概率就越大。因为在某段时间内，越短的路径就会被越多的蚂蚁选中，则积累的信息素浓度随之提高，在后续时间内被其他蚂蚁选中的概率也随之越大。持续重复这个过程，直到几乎所有的蚂蚁都选择最短的路径为止，那么这条路径也就是蚁群选择的最优或者次优航路[10]。

2.2 航路点选择规则

将无人机的起飞点视为蚁巢，目标点视为蚁群的食物源，这样蚁群寻找最优或者次优路径的过程就是对无人机进行航路规划的过程。蚁群基于信息素浓度和可见度选择下一段航路或者目标点，在t时刻第k只蚂蚁从当前节点i转移到下一节点j的转移概率为：

(4)

其中：τij(t)为节点i与节点j连接路径上的信息素浓度，ηij(t)为启发函数，经典蚁群算法中该函数为节点i到节点j的距离倒数，表示蚂蚁转移到节点j的期望程度；allowk为蚂蚁k即将访问的航路点的集合；参数α和β分别表示为信息素重要程度因子和能见度重要程度因子。

蚂蚁在释放信息素的同时，各条航路上的信息素浓度逐步降低，令ρ表示信息素的挥发因子，因此当所有蚂蚁完成一次搜索后，仅对成功搜索到目标点的蚂蚁所经历过的航路上的信息素进行更新，即：

(5)

(6)

2.3 蚁群算法的改进

采用基本蚁群算法为无人机规划航路时，分析实验结果可明显发现基本蚁群算法具有收敛速度慢、易于陷入局部最优的缺陷[11]。出现这种现象的原因是局部航路上的信息素堆积过量，这些浓度过高的信息素会对后到的蚂蚁在选择航路上造成影响，导致大量的蚂蚁集中于此航路，最终导致算法出现早熟。因此直接将蚁群算法应用于无人机航路规划问题欠妥。为了克服这些缺点，本文对基本蚁群算法进行了如下改进。

2.3.1 改进航路点选择策略

传统蚁群算法发生状态转移时，采用概率随机选择策略，这种策略缺乏引导因素，致使算法进化缓慢。因而本文从航路点选择策略入手进行改进，引入随机选择和伪随机性选择相结合的选择策略，如公式(7)，并且在搜索过程中动态调整作伪随机性选择的概率，这样可以有效降低蚂蚁在搜索过程中的盲目性。当搜索进行至一定代数时，搜索方向已经趋于稳定，此时可以适当增加作随机选择的概率，以方便对解空间的更充分的搜索，从而达到克服基本蚁群算法不足的目的。

在t时刻，蚂蚁从k按照下式确定下一时刻将要到达的航路点j：分别

(7)

式中，预先定义q0∈[0,1]，q为[0,1]上服从均匀分布的随机数，α、β的含义同公式(4)，采用该改进的选择策略，可以随着搜索的进行动态调整q0的值，当q≤q0时，可以选择改进的移动规则，由信息素浓度和启发函数联合决定蚂蚁最佳的选择方向；当q>q0时，可以执行有诱导的探索，确保算法的收敛。使用该改进规则的主要目的不仅是节省搜索时间加快收敛速度，而且还能增强搜索的多样化，避免停滞状态的过早发生。

排砂冷采不进行防砂，所以单井出砂量很大。排砂冷采完全依靠天然能量进行开采，初期产量很高，但是持续时间比较短，采收率较低。由于地层形成了“蚯蚓洞”所以若后期转注水和注汽措施容易发生气窜水窜，另一方面“蚯蚓洞”一旦遭遇边底水入侵开采效果将会剧降。

2.3.2 改进信息素挥发因子调整准则

蚁群算法中，信息素挥发因子ρ的取值与算法的全局搜索能力及其收敛速度密切相关，ρ的初始值直接影响各条航路上信息素的分布。基本蚁群算法中，ρ值保持不变。当无人机规划空间较复杂时，由于信息素挥发因子ρ的存在，将导致未被搜索到的节点上的信息素浓度持续降低甚至逼近0的情况，影响了算法的全局搜索能力。ρ过大时，虽然会加快算法收敛，但易于陷入局部最优；ρ过小时，以前搜索过的节点被再次选择的概率较大，又会影响算法的的收敛速度。鉴于此，本文受最大-最小蚂蚁系统思想的启发[12]，给信息素挥发因子ρ设定上限和下限，在采用蚁群算法求解过程中，当迭代一定次数求得的最优值没有显著改善时，采用式(8)对ρ进行调整：

(8)

式中，ρmin、ρmax分别表示信息素挥发因子ρ的下限和上限，设定ρ的上下限，可以有效避免算法的易于陷入局部最优和收敛速度慢的缺点。λ为引入的挥发约束系数，λ∈(0,1)，为了更加精确地模拟信息素的挥发情况，引入了一种随机函数，即rand(t+1)，该函数的取值为(0.75, 0.95)的随机数，并利用该随机函数对挥发约束系数λ进行如下修正[13]：

(9)

采用引入随机函数的机制，使得信息素能够按照一种随机的方式进行挥发，确保了信息素的更新更加符合自然界真实情况。将式(5)中的信息素挥发因子ρ用ρ(t)替代，使得信息素τ也随之更新。每当循环结束时，保留最优解，将其作为判断ρ如何调整的条件。

2.4 改进蚁群算法实现过程

采用改进蚁群算法为无人机规划航路的步骤如下。

Step 1：初始化无人机飞行区域所有航路点的信息素，即构造初始信息素矩阵；

Step 2：M只蚂蚁置于起始点S处待出发；

Step 3：蚂蚁依据公式(4)、(7)由当前航路点选择下一航路点，如此迭代下去，直到抵达目标点，得到一条可飞航路。所有蚂蚁均执行此过程。

Step 4：依据公式(3)对蚂蚁得到的所有可飞航路进行代价评估，保存所找到的最优航路。

Step 5：对飞行区域中的各航路点按公式(5)、(6)进行信息素调整。

Step 6：依据最优解判断是否需要进行ρ值的调整，如需要则按照公式(8)、(9)进行信息素挥发因子的自适应调整。

Step 7：判断是否已经满足循环结束条件，即是否达到既定的迭代次数或找到最优解，如果满足则结束循环，否则转至Step 2继续执行，直至满足迭代条件。

3 航路的优化处理

以上改进的蚁群算法规划出的航路存在拐角，如图3所示，无人机在这样的航路上飞行需要频繁的制动操作，这会增加无人机的飞行风险，对无人机的结构性能也是一种考验，所以要对这些存在拐角的航路进行平滑处理。无人机的最小转弯半径按如下公式计算[14]：

(10)

图3 存在拐角的航路

如图4所示，如果3个航迹点Pi-1、Pi、Pi+1构成的航路段存在夹角，则以无人机最小转弯半径做拐角的内切圆，用内切圆的圆弧部分取代该拐角部分，使得航路平滑可飞。

图5和图6分别是改进蚁群算法平滑之前和平滑之后的航路，通过对比可以发现经过平滑处理的航路消除了原有航路上存在拐角的地方，这样的航路更加满足无人机实际飞行需求。

图4 航路优化示意图

4 航路的预规划与重规划

无人机实际执行任务时应该首先根据已知的情报信息规划出一条最优或者次优的飞行航路，无人机先按照该航路飞行，飞行过程中由无人机机载雷达等设备不断地对周围环境进行检测；当检测到突发威胁后，无人机将判断预规划的航路是否处于改为的有效杀伤范围，若不在有效杀伤范围内，则无人机按原有航路飞行，若在有效杀伤范围内，则无人机以当前点位新的出发点重新规划航路，以确保能够躲避检测到的突发威胁。重规划流程图如图5所示。

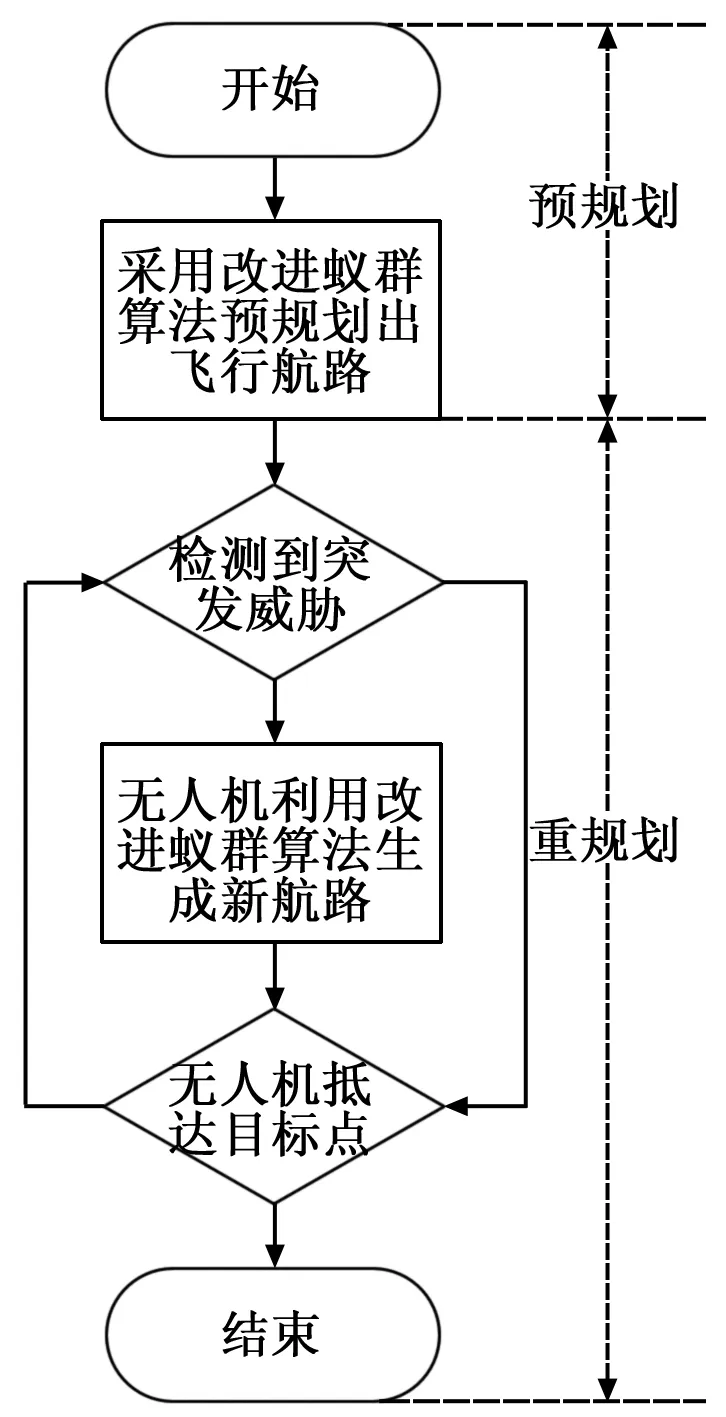
图5 重规划流程图

5 实验仿真与结果分析

5.1 实验仿真

为了验证以上提出的改进蚁群算法在解决无人机航路规划问题的有效性，这一部分在Windows 8操作系统中使用matlab 8.1平台进行仿真，硬件配置为：英特尔i5-2400 @ 3.10GHz 处理器，4GB内存。仿真时使用的相关参数，ω1=0.4，ω2=0.4，ω3=0.2，M=90，Q=100，α=1,β=4,q0=0.8，ρmin=0.1，ρmax=0.95，无人机飞行区域内，起始点S和目标点G的坐标分别为(10,10)和(10,10)，有3种威胁源分布在这两点之间，不同种类的威胁源的威胁半径不同，表1所示是6个威胁源的圆心位置坐标和攻击半径。

表1 6个威胁源的分布

针对上述只存在静态威胁的飞行环境，分别采用基本蚁群算法、遗传算法和改进蚁群算法进行仿真，设定各算法迭代次数均为300次。图6为3种仿真效果图，其中的航路均已进行平滑优化。

图6 静态环境下3种算法航路规划示意图

另外，为了验证改进蚁群算法躲避具有规避动态威胁能力，在上述飞行环境的基础上加入动态威胁，用虚线圆模拟该动态威胁，图7为3种算法仿真效果图，其中的航路均已进行平滑优化。

图7 动态威胁下3种个算法航路规划示意图

5.2 实验结果分析

针对只存在静态威胁和存在动态威胁两种飞行环境，基本蚁群算法、改进蚁群算法和遗传算法的性能分析分别如表2、3和图8、9所示。从表2和图8可以看出，在只存在静态威胁的飞行环境下，与基本蚁群算法和遗传算法相比，改进蚁群算法能在相对较短的时间内搜索出最优航路；从表3和图9可以看出，在存在动态威胁的飞行环境下，与基本蚁群算法和遗传算法相比，改进蚁群算法也能用较短的时间搜索出最优航路。

表2 静态威胁下各算法性能对比

表3 动态威胁下各算法性能对比

图8 静态威胁中3种算法收敛图

图9 静态威胁中3种算法收敛图

6 结论

传统的蚁群算法在解决无人机航路规划时存在易于陷入局部最优，收敛速度慢的问题，鉴于此，对传统的蚁群算法做了改进，提出航路点的自适应选择策略和信息素挥发因子自适应调整准则，并进行了仿真，实验结果表明改进蚁群算法有效克服了基本蚁群算法的不足，并与遗传算法做了对比，对比显示改进的蚁群算法在搜索时间和搜索的航路长度上优于遗传算法，还引入了在线重规划机制，该机制提高了无人机在真实战场环境下的作战能力。

[1] 李士波, 孙秀霞, 王 栋，等. 无人机动态环境实时航迹规划[J].

系统工程与电子技术, 2007,29(3):399-401.

[2] Qian X, Peng C, Nong C. Offline Path Planning and Online Replanning of UAVs in Complex Terrain[A]. Proceedings of 2014 IEEE Chinese Guidance, Navigation and Control Conference[C]. Yantai, China, 2014:2287-2292.

[3] He Y F, Zeng Q H, Liu J Y, et al.Path Planning for Indoor UAV Based on Ant Colony Optimization[A]. 2013 25th Chinese Control and Decision Conference[C]. Guiyang, China, 2013: 2913-2923.

[4] 潘广贞, 秦 帆, 张文斌. 动态自适应快速扩展树航迹规划算法研究[J]. 微电子学与计算机, 2013,30(1):49-52.

[5] 张淘沙, 鲁 艺, 张 亮，等. 改进型Voronoi图和动态权值A*算法的无人机航迹规划[J]. 火力与指挥控制, 2015,40(2):156-160.

[6] 唐 强, 王建元, 朱志强. 基于粒子群优化的三维突防航迹规划仿真研究[J]. 系统仿真学报, 2004,16(9): 2033-2036.

[7] 刘振峰, 谢洪森, 危水根. 基于蚁群遗传算法的三维飞行器航路规划[J]. 计算机仿真, 2013,30 (9): 121-125.

[8] Vincent Roberge, Mohammed Tarbouchi, Gilles Labonté. Comparison of Parallel Genetic Algorithm and Particle Swarm Optimization for Real-Time UAV Path Planning[J]. IEEE Transaction on Industrial Informatics, 2013, 9(1):132-141

[9] 柳长安, 梁广平, 王和平，等. 蚁群算法在无人机航路规划中的应用[J]. 火力与指挥控制, 2005, 30(6):22-24.

[10] 邱小湖,邱永成. 优化蚁群算法在无人机航路规划中的应用[J]. 计算机仿真, 2010, 27(9):102-105.

[11] 柴毅哲, 杨任农, 马明杰，等. 基于改进蚁群算法的可规避威胁源最优航线规划[J]. 空军工程大学学报(自然科学版), 2015,16(2):23-27.

[12] 黄永青, 杨 凡, 张峻岭，等. 一种交互式最大最小蚂蚁算法[J]. 计算机工程, 2012,38(20):128-131.

[13] 邬 琦, 潘广贞, 杨江涛. 基于Voronoi图和动态自适应蚁群算法的UAV航迹规划[J]. 计算机测量与控制, 2014,22(9):3037-3037.

[14] Wen N F, Zhao L L, Su X H, et al. UAV Online Path Planning Algorithm in a Low Altitude Dangerous Environment[J]. IEEE/CAA Journal of Automatica SINICA,2015,2(2).

UAV Route Planning in Dynamic Environment Based on Modified Ant Colony Opimization

Lin Na， Liu Erchao

(College of Computer Science, Shenyang Aerospace University, Shenyang 110136, China)

On the research of route planning for UAVs, the basic Ant Colony Optimization algorithm is easily trapped into local optimal and takes very long time to plan the route, so the Ant Colony Optimization is modified in this paper; by introducing dynamic adaptive route selection and pheromone evaporation factor dynamic adaptive criteria, we overcome the shortage of basic Ant Colony Optimization algorithm effectively, at the same time measures are taken to smooth the planned route to make it meet the demand of UAVs’ flight. By simulation, we get the routes in static threat environment and dynamic threat environment respectively, the results show that modified Ant Colony Algorithm can map out optimal routes in both environment.

UAVs; ant colony optimization; selection strategies; pheromone; smoothing

2015-08-25；

2015-10-26。

辽宁省自然科学基金联合基金(2015020008)；辽宁省自然科学基金(20102175； 201102171)；辽宁省高等学校优秀人才支持计划(LJQ2012011)；辽宁"百千人才工程"人选项目(2010921080；2009921089)。

林 娜，辽宁沈阳人，博士，副教授，主要从事智能交通，下一代网络，无人机航迹规划方向的研究。

1671-4598(2016)03-0149-05

10.16526/j.cnki.11-4762/tp.2016.03.041

TP311

A