基于遗传-模拟退火的蚁群算法求解TSP问题

徐 胜，马小军，钱 海，王震宇

(南京工业大学 电气工程与控制科学学院，南京 211800)



基于遗传-模拟退火的蚁群算法求解TSP问题

徐 胜，马小军，钱 海，王震宇

(南京工业大学 电气工程与控制科学学院，南京 211800)

传统的蚁群算法具有收敛性好、鲁棒性强等优点，但在解决旅行商(TSP)问题方面存在收敛时间长，容易出现停滞等问题;为了提高传统蚁群算法的解的质量，本文提出了基于遗传-模拟退火的蚁群算法(G-SAACO)，将遗传算法和模拟退火算法引入蚁群算法中;其方法是在传统蚁群算法中引入遗传算法的变异与交叉策略来得到候选解，增加解的多样性;同时引进模拟退火算法机制，使得在高温时以较高概率选择候选集中比较差的解加入最新集，温度控制上加入了回火机制，进一步提高解的质量;为了检验改进的蚁群算法，随机选用了TSPLIB中的部分城市进行仿真，结果与传统蚁群算法、模拟退火蚁群算法、遗传蚁群算法相比，算法具有较强的发现较好解的能力，同时增强了平均值的稳定性。

传统蚁群算法；遗传算法；模拟退火；旅行商问题

0 引言

在20世纪50年代中期，人们从生物行为和生物进化的机理中获得启发，提出了各种用来解决优化问题的方法，如遗传算法、禁忌搜索、模拟退火、进化策略等。20世纪90年代，意大利学者Dorigo等人通过观察蚂蚁觅食的行为提出了蚁群算法(ACO)[1]。蚁群算法利用了蚁群觅食的正反馈原理，具有收敛性好、鲁棒性强、并行性好等优点，使得其在解决TSP问题方面优于模拟退火算法、禁忌算法、遗传算法等智能算法[2-3]。但同时也存在收敛时间长，容易出现停滞等问题。文献[4]中张晓婧等人提出的模拟退火蚁群算法在求解Job-Shop问题时，虽然提高了算法的收敛速度，但导致了早熟现象。文献[5]中江新姿等人提出的求解旅行商问题的模拟退火蚁群算法，在一定程度避免了早熟现象，但收敛速度变慢了。

本文将遗传算法和模拟退火算法引入蚁群算法中，在对原有算法改进的基础上，提出了一种基于遗传-模拟退火的蚁群算法。此算法利用遗传算法对蚁群算法得到的解进行交叉变异操作，从而获得新解，把蚁群算法的解和遗传算法的解组合成候选集，扩大了解的范围，并在一定程度上避免了早熟现象。同时结合模拟退火算法机制，使得在高温时能够以较高的概率选择候选集中比较差的解加入最新集，增加了解的多样性，很好的防止了早熟现象的发生；在低温时较差的解只有很小的概率才会被加入到最新集，这有效地提高了算法的收敛速度。在温度控制上加入了回火策略，进一步提高解的质量。

1 传统蚁群算法求解TSP问题

1.1 TSP问题描述

设有n个城市， 为任意两个城市i，j之间的距离，求经过每个城市有且仅有一次的一条路径M=(M(1)，M(2)，…，M(n))，使得

1.2 传统蚁群算法的TSP求解

意大利学者M.Dorigo等人发现:蚂蚁在运动过程中会在所经过的路径上留下一种称之为信息素的物质，而且它们能够感知到这种物质，并倾向于朝该物质强度高的方向移动[6]。因此，由大量蚂蚁所组成的集体行为就表现出一种信息正反馈现象:某一路径越短，那么该条路径上走过的蚂蚁就越多，所留下的信息素的强度自然也就越大，后来者选择该条路径的概率也就越大。蚂蚁个体之间通过这种信息交流来选择最短路径并达到搜索食物的目的。

在旅行商问题中，设m为蚂蚁总数，表示t时刻位于城市i的蚂蚁数，则。为t时刻边上信息素的强度，设 (C为常数)。随着时间的推移，先前的信息素会挥发，而新的信息素会加入，ρ为信息素保留程度，1-ρ为信息素消逝程度，当m只蚂蚁都完成一次循环后，各边的信息素按下面公式调整：

(1)

(2)

表示第k只蚂蚁留在路径ij上的信息素，为此次循环中边ij上的信息素增量。

(3)

(4)

Lk为本次循环后，第k只蚂蚁的路径长度，Q为常数。

在循环过程中，由转移概率决定转移方向，表示第k只蚂蚁从城市i转移到城市j的概率。

(5)

ηij为边(i，j)的能见程度，是某种启发信息，信息素和能见程度的相对重要性，={0，1，2，3，…，n-1}-tabuk表示允许蚂蚁k选择城市的集合，是蚂蚁k的禁忌表，用来记录蚂蚁k已走过的城市，体现了人工蚂蚁的记忆性。

传统蚁群算法解TSP问题的基本步骤。

Step1：迭代步数nc←0，τij→C(C为常数)，τij←0，将m只蚂蚁随机放在n个顶点上；

Step3：当各蚂蚁k完成本次循环后，计算各只蚂蚁的路径长度Lk，并按照式(1)来更新信息素；

Step4：nc←nc+1；

Step5：如果nc<总迭代步数，则转步骤2；

Step6：根据各路径上信息素的强度，得出最好解。

2 遗传-模拟退火的蚁群算法

在求解TSP组合优化问题时，蚁群算法是在整个可行解内进行盲目的随机搜索全局最优解，因此就产生了算法的收敛速度慢、易于停滞等问题，为了很好的克服这些问题。本文对传统蚁群算法作了一些改进。

2.1 遗传算法的引入

遗传算法是以“适者生存”和遗传变异理论为基础的一类仿生优化算法。本文利用遗传算法的交叉和变异的策略来改善蚁群算法的解的多样性。

遗传算法对蚁群算法得到的解集path1中的解与path1中的最优解pbest1按概率交叉操作得到解集path2，然后再对path1中的解按概率进行变异操作获得解集path3，最后将path1、path2和path3组合成候选集path。

交叉策略：在pbest1中随机选择一个交叉区域，删除待交叉解中已在pbest1的交叉区中出现过的城市，将pbest1的交叉区域加到待交叉解的随机位置上。例如：pbest1=1，2，3，4，5，6，7，8；交叉区域为：5 6 7 8；待交叉解为8，7，6，5，4，3，2，1；随机位置为3，交叉后为：4，3，2，5，6，7，8，1。

变异策略：随机选择待变异解的第次和第次访问的城市，在待变异解中交换这两次访问的城市，其他不变。例如：待变异的解为8，7，6，5，4，3，2，1；=1，=4；则变异之后的解为5，7，6，8，4，3，2，1。

2.2 模拟退火算法的引入

2.2.1 模拟退火机制的引入

本文利用模拟退火机制由候选集path生成最新解pathnew，逐个计算候选集中的解，按照下列公式决定候选集中的解是否加入最新集。

(6)

其中：ΔL=Lw-Lwmin，表示候选集中第w个解的路径长度，表示候选集中最短的路径长度，T为当前温度值。若，则将第w个解加到最新集pathnew中；否则在[0，1)之间产生一个随机数，若，则第w个解进入最新集pathnew。

由式(6)可知：在高温时以较高概率选择候选集中比较差的解加入最新集，增加了解的多样性，在一定程度在避免了早熟和停滞现象。在低温时比较差的解只有很小的概率加入最新集中，这样加快了算法的收敛速度。

2.2.2 回火机制

在完成一次循环和信息素的更新后，温度T按照下列式子进行降温：

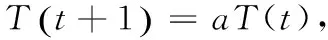
(7)

从式(7)可以看出：如果取较小的降温系数a，这样可以加快算法的速度，但很可能算法会陷入局部最优。为了克服这个困难，本文运用了回火策略，当温度T下降到T1时，算法立即温度T升到T2，同时可以设定回火次数G，最大回火次数Gmax。

回火策略很好的发挥了模拟退火机制的作用。当温度T上升到T2时，以较高概率选择候选集中比较差的解加入最新集，大大减少了落入局部最优的风险。

2.3 信息素的更新

2.4 算法的描述

遗传-模拟退火的蚁群算法的步骤如下。

Step1：初始化算法参数m,T,T1,T2,a,α,β,ρ,Gmax,Q,Pc,Pm,τij=C,Δτij=0,t=0将所有的蚂蚁都放在城市1；

Step2：第k只蚂蚁按转移概率移动到j城市；

Step3：当m只蚂蚁都完成了一次循环，蚁群得到解集path1，path1内最优解为pbest1；

Step4：解集path1中的解逐个按概率pc与pbest1进行交叉操作，获得解集path2；

Step5：解集path1中的解逐个按概率pm进行变异操作，得到解集path3；

Step6：解集path1、path2和path3组合成候选集path，记录当前最优解gbest；

Step7：根据模拟退火机制，按照概率pw来选择path中的解，生成最新集；

Step8：根据最新集里的解按照式(1)～式(4)对信息素进行更新；

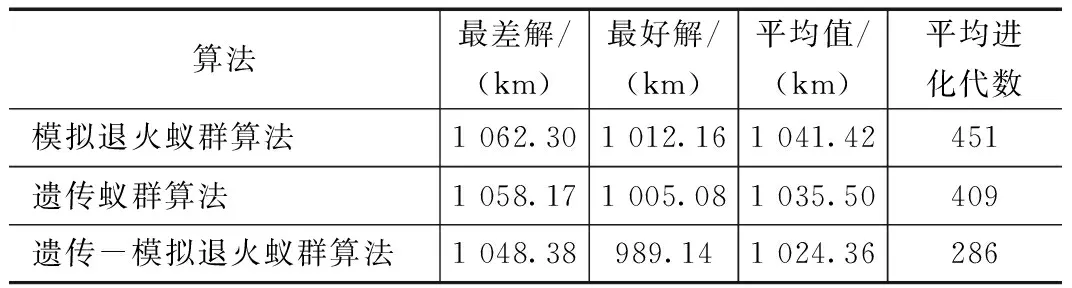
Step9：T←aT，t←t+1；若T≥T1，则转到Step2；若T

3 算法测试

为了检验本文算法，随机选用了国际上通用的TSP测试库TSPLIB中a280(280个城市)里的50个城市来进行仿真，并且与传统蚁群算法、模拟退火蚁群算法、遗传蚁群算法进行比较。传统蚁群算法参数如下：蚂蚁数m=30，信息素保留程度ρ=0.9，信息素的重要程度α=1.5，能见性的重要程度β=2，初始信息素C=100；采用文献[5]中的模拟退火蚁群算法，初始温度T=100 000，终止温度T0=10，降温系数a=0.9；采用文献[8]中的遗传蚁群算法，染色体数N=30，交叉概率Pc=0.4，变异概率Pm=0.1；本文算法参数设计：m=30，ρ=0.9，α=1.5，β=2，C=100，Q=100 000，a=0.9，T=5 000，T1=100，T2=2 000，Gmax=8，Pc=0.4，Pm=0.1。对各种算法测试50次，结果如表1所示。图1是遗传-模拟退火蚁群算法最好的解，总路程为989.14 km。

从表1中的最好解一列可以看出遗传-模拟退火蚁群算法具有较强的发现较好解的能力。观察他们的平均值可以知道本文算法也具有较好的稳定性。

4 结论

采用传统算法改进后的遗传-模拟退火蚁群算法来求解TSP问题能够获得比模拟退火算法、标准遗传算法和传统蚁群算法都要好的解，而且也增加了解的多样性和稳定性，同时算法的收敛度也得到了一定程度的改善，证明了该算法具有一定的有效性。

表1 3种算法的测试结果

图1 用遗传-模拟退火蚁群算法解TSPa280最好的解

[1]宋志飞.基于蚁群算法的TSP问题研究[D].江西:江西理工大学,2012.

[2]吴华锋，陈信强，毛奇凰，等.基于自然选择策略的蚁群算法求解TSP问题[J].通信学报,2013,34(4):165-170.

[3]侯文静，马永杰，张 燕，等.求解TSP的改进蚁群算法[J].计算机应用研究,2010,27(6): 2087-2089.

[4] 张晓婧，高慧敏.基于模拟退火的蚁群算法求解Job-Shop问题[J].计算机应用与软件，2008,25(5): 77-79.

[5]江新姿，高 尚，陈建忠.求解旅行商问题的模拟退火蚁群算法[J].计算机工程与设计,2008,29(6): 1491-1493.

[6] 刘 波,蒙培生.采用基于模拟退火的蚁群算法求解旅行商问题[J].华中科技大学学报(自然科学版), 2009, 37(11): 26-30.

[7] 陈冰梅，樊晓平，周志明，等.求解旅行商问题的Matlab 蚁群仿真研究[J]. 计算机测量与控制,2011,19(4): 990-997.

[8]江君莉，潘 丰.求解TSP的遗传蚁群融合算法[J].江南大学学报(自然科学版),2012,11(3):253-256.

Genetic-simulated Annealing-based Ant Colony Algorithm for Traveling Salesman Problem

Xu Sheng， Ma Xiaojun， Qian Hai， Wang Zhenyu

(College of Electrical Engineering and Control Science，Nanjing Tech University，Nanjing 211800，China)

The traditional ant colony algorithm has the advantages of good convergence and robustness, but has a long convergence time in solving the problem of TSP. In order to improve the quality of the solution of the traditional ant colony algorithm， G-SAACO is proposed，the genetic algorithm and simulated annealing algorithm are introduced into the ant colony algorithm.. The idea of the algorithm was to introduce the variation and crossover strategy of genetic algorithm into the traditional ant colony algorithm to get the candidate solutions， which increased the diversity of the solution. And introduction of simulated annealing algorithm mechanism made the algorithm have higher probability of selecting poor solutions in a candidate set into the latest set. Besides，In the mechanism of controlling the temperature， the quality of the solutions was improved through backfire strategy. In order to test the improved ant colony algorithm, randomly selected parts of the city of the TSPLIB to simulate.Compared with the standard GA，simulated annealing algorithm and the traditional ant colony algorithm for traveling salesman problem(TSP).The results show that the algorithm has a strong ability to find good solutions, and the stability of the average value is enhanced.

traditional ant colony algorithm；genetic algorithm；simulated annealing；traveling salesman problem

2015-08-28；

2015-11-16。

江苏省普通高校研究生科研创新计划项目(SJLX_0334)。

徐 胜(1990-)，男，江苏常熟人，研究生，主要从事建筑智能化技术方向的研究。

马小军(1956-)，男，江苏南京人，教授，主要从事建筑智能化技术，PLC，嵌入式技术方向的研究。

1671-4598(2016)03-0143-02

10.16526/j.cnki.11-4762/tp.2016.03.039

TP18

A