运输机重装空投二阶终端滑模控制方法研究

王文星，雒东超，张晓敏，孙秀霞，王 栋

(1.中国飞行试验研究院 中航工业飞行仿真航空科技重点实验室，西安 710089；2.空军工程大学 航空航天工程学院，西安 710038)



运输机重装空投二阶终端滑模控制方法研究

王文星1，雒东超1，张晓敏1，孙秀霞2，王 栋2

(1.中国飞行试验研究院 中航工业飞行仿真航空科技重点实验室，西安 710089；2.空军工程大学 航空航天工程学院，西安 710038)

针对重装空投过程中，货物的持续移动及瞬间出舱影响空投任务完成性、威胁飞行安全等问题，提出了一种二阶终端滑模纵向飞行控制方法；该方法利用非线性多输入多输出反馈线性化完成系统解耦线性化，在此基础上采用二阶终端滑模变结构控制设计系统内环速度与俯仰姿态跟踪控制器，保证了系统鲁棒性，结合外环PID高度保持控制器完成了整个飞行控制系统的设计；数值仿真结果表明，该系统具有良好的响应特性，且对系统不确定性具有较强的鲁棒性。

非线性系统；飞行控制；终端滑模；二阶滑模

0 引言

超低空空投主要用于重型装备的精确投放，是大型运输机必备的功能之一[1-2]。在空投过程中，重型货物的持续移动及瞬间离机将对飞机产生较大干扰，致使飞机的姿态和轨迹发生大幅度偏离，严重威胁飞行安全[3]。因此，针对运输机重装空投飞行控制方法的研究具有重要的意义。

当前，针对重装空投过程的飞行控制问题，许多学者做出了卓有成效的研究：文献[4]提出了基于L1自适应理论的飞行控制方案；文献[5-6]基于在线提供的重心信息，采用逆动力学和均衡式自动驾驶仪控制律，设计了一类变重量、变重心飞机姿态控制律；文献[7]提出了一种基于动态逆和鲁棒控制相结合的全维重装空投控制律；文献[8-9]基于空投过程反馈线性化模型，设计了线性滑模飞行控制器。其中，基于滑模变结构理论的飞行控制方法在应对系统参数不确定性方面具有很好的效果，但是线性滑模控制方法的收敛时间长，不能够满足重装空投高时效性的要求。

本文综合二阶滑模和终端滑模的优点，设计了二阶终端滑模空投飞行控制器。通过合理选择系统状态，保证反馈线性化的实时可逆解耦，实现了多变量交叉耦合空投模型解耦线性化。在此基础上，设计二阶终端滑模控制器稳定系统内环速度和姿态，提高了控制的快速性和准确性，解决了空投系统模型不确定性等问题。结合外环PID高度跟踪控制完成整个飞行控制系统的设计。

1 空投过程飞机运动方程

考虑重装空投过程纵向数学模型[4]

(1)

其中:H,V,α,q,θ,γ分别表示飞机高度、速度、迎角、俯仰角速度、俯仰角、爬升角；m,mc,Iy,rc分别表示空机质量、货物质量、飞机绕横轴转动惯量、货物相对于飞机质心位移；L、D及My分别为升力、阻力和俯仰力矩。货物相对飞机质心的位移rc为：

(2)

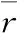
(3)

式中，TδT为推力系数，δT为油门开度。升力、阻力和俯仰力矩的表达式为：

(4)

式中，δe是升降舵偏角; L0,D0及M0为初始升力、阻力和俯仰力矩; x*表示x相对*的气动导数。

结合式(1)～(4)，同时考虑系统模型不确定性，则飞机运动方程可写成如下形式：

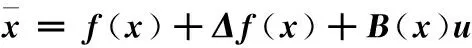
(5)

式中，x=[V,α,q,θ]T，u=[δe,δT]T，

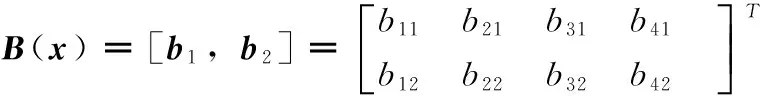
f(x)=[f1,f2,f3,f4]T，Δf(x)=[Δf1,Δf2,Δf3,Δf4]T为系统不确定性函数。fi和bij(i=1,2,3,4;j=1,2) 的表达式为:

2 模型的输入输出反馈线性化

选取y=[h1h2]T=[V θ]T作为系统(5)的输出状态。应用反馈线性化方法[10]可将系统(5)化为如下的输入输出形式:

(6)

(7)

其中:L(·)为李导数算子。由计算可知，r1=1，r2=2。

系统解耦矩阵E(x)为:

(8)

(9)

3 控制律设计与稳定性分析

本文设计的控制律包含两个回路，如图1所示。外回路以飞机俯仰角θ作为控制量，采用PID控制器实现对高度指令Hd的跟踪，内回路采用二阶终端滑模控制方法，以升降舵和油门开度作为控制量，跟踪外回路期望俯仰角θd和期望速度Vd。

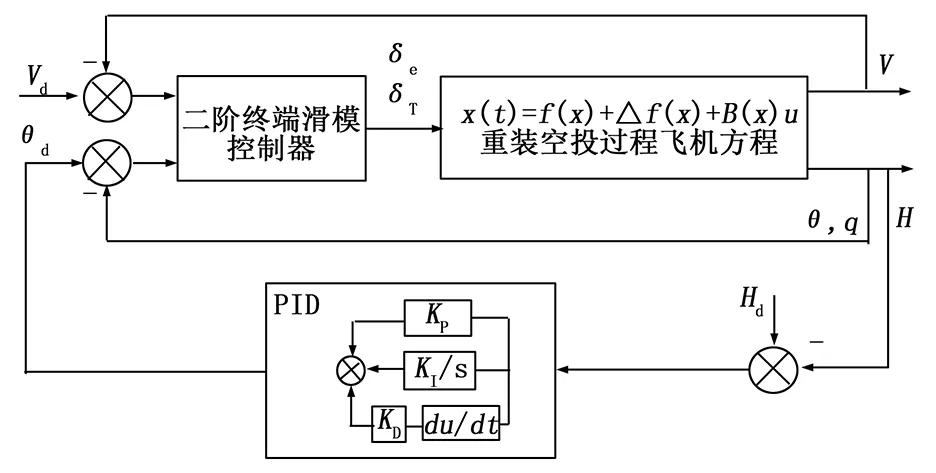
图1 控制系统结构

考虑系统(6)，设计二阶终端滑模控制律稳定飞机速度和俯仰姿态。定义速度和俯仰角的跟踪误差为：

(10)

式中，Vd和θd为空投启动时飞机的配平速度和俯仰角。

设计滑模面函数为:

(11)

为保证滑模函数s1和s2在有限时间内收敛到平衡点，设计如下的二阶滑模函数

(12)

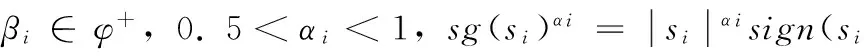
令S=[s1s2]T，Ζ=[z1z2]T, 则有:

(13)

(14)

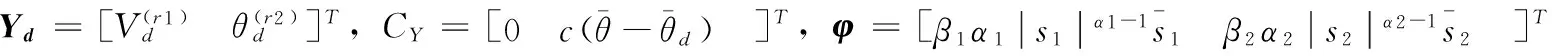
设计到达律为:

(15)

由式(15)可知，存在一个有限时间ti1，使得zi由初始值zi(0)≠0收敛至0。

(16)

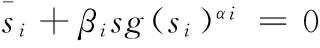
(17)

设计控制作用为:

(18)

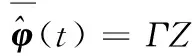
(19)

其中:Γ∈φ+为自适应增益。

为证明滑模面在控制律(18)和自适应律(19)的作用下可达，定义如下的Lyapunov函数：

(20)

由式 (11)和(14)可得υ的一阶导数为:

(21)

将控制律(18)代入式(21)可得:

(22)

将自适应律(19)代入式(22)可得:

(23)

即滑模面可达性条件成立。

4 仿真与分析

基于本文设计的重装空投控制器，以某型运输机为例，在H=10 m高空，采用单列单投模式完成仿真实验。假设模型存在±20%的误差，飞机配平参数为：速度V=80 m/s，迎角α=θ=3.526 9°，油门开度δT=25.1%，升降舵偏度δe=0°。仿真主要验证控制器的控制性能和鲁棒性。选取内环二阶终端滑模控制参数为：c=2，β1=β2=2,α1=α2=0.7，k1=k2=1.6，ε1=ε2=0.01，p1=p2=0.5，Γ=1。外环PID高度保持控制器参数为Kp=0.15，KI=0.1，KD=0.002 7。

图2(a)～(d)分别对应飞机高度、速度、俯仰角和迎角曲线。由图中实线可见，空投过程中飞机高度变化量在0.2 m范围内，大约货物离机6 s后高度稳定于配平状态值，飞机速度在整个过程变化很小。迎角和俯仰角的变化量被控制在2°以内，而由于重型货物的离机，飞机再次稳定时的迎角和俯仰角明显小于飞机带货配平状态。从图中点划线和虚线也可看出，当考虑气动参数不确定性时，控制器仍能保证良好的控制效果。图3(a)和(b)分别为升降舵偏转和油门开度曲线。可以看出升降舵偏转和油门开度幅值均在允许范围内，未出现强烈的抖振现象。

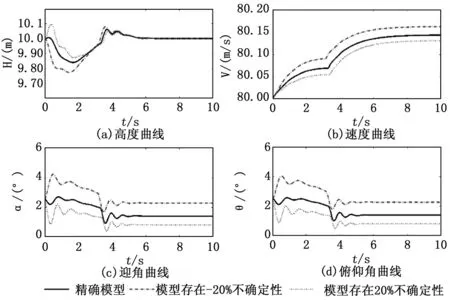
图2 空投过程飞机响应曲线

图3 升降舵和油门开度曲线

5 结论

重装空投过程是一个强耦合、强非线性、存在突变等强干扰的不确定系统，本文设计了基于反馈线性化和二阶终端滑模变结构方法相结合的重装空投纵向控制器。在合理选取系统状态变量，保证系统实时可逆解耦的基础上，理论证明了控制器的鲁棒稳定性，最后，通过模型存在摄动情况下的仿真试验，验证了控制器的强鲁棒性。

[1] Zang J, Liu Hu, Liu TP, Ni XP. Object-oriented mission modeling for multiple transport aircraft [J]. International Journal of Aeronautical and Space Sciences, 2013, 14(3): 264-271.

[2]Desabrais K J, Riley J, Sadeck J, Lee C. Low-cost high-altitude low-opening cargo airdrop Systems [J]. Journal of Aircraft, 2012, 49(1), 349-354.

[3]Liu R, Sun XX, Dong WH. Dynamics modeling and control of a transport aircraft for ultra-low altitude airdrop [J]. Chinese Journal of Aeronautics, 2015, 28(2): 478-487.

[4]孙秀霞, 常允刚, 董文瀚,等. 最优控制L1自适应在重装空投纵向控制器设计中的应用[J]. 控制理论与应用, 2015, 32(5): 598-606.

[5]杨晓科, 杨凌宇, 张晶等. 变重量/重心飞机建模及姿态控制律设计[J]. 北京航空航天大学学报, 2011, 37(1): 54-57.

[6]张 晶, 申功璋, 杨凌宇. 基于逆动力学和重心估计的飞行控制系统设计[J]. 北京航空航天大学学报, 2009, 35(11): 1315-1319.

[7]冯艳丽, 史忠科. 超低空空投货物出舱过程的动态逆鲁棒控制[J]. 控制工程, 2010,17(5): 579-583.

[8]Zhang H Y, Shi Z K. Variable structure control of catastrophic course in airdropping heavy cargo [J]. Chinese Journal of Aeronautics, 2009, 22(2): 520-527.

[9]Liu R, Sun XX, Dong WH. Flight controller design for aircraft low altitude airdrop [J]. Aircraft Engineering and Aerospace Technology, 2016, 88(4), 1-11.

[10]胡跃明. 非线性控制系统理论与应用[M]. 北京: 国防工业出版社, 2003.

Second-Order Terminal Sliding Mode Control of a Transport for Heavyweight Airdrop

Wang Wenxing1, Luo Dongchao1, Zhang Xiaomin1, Sun Xiuxia2, Wang Dong2

(1.AVIC Aeronautical Science and Technology Key Laboratory of Flight Simulation,CFTE, Xi’an 710089, China；2.Aeronautics and Astronautics Engineering College, Air Force Engineering University, Xi’an 710038, China)

In order to dealing with the influence caused by the continuous movement of the cargo and its sudden deplaning during airdrop operations, a novel flight controller based on the second-order terminal sliding mode control approach is designed. This method uses the feedback linearization technique to decouple the nonlinear airdrop model. On this basis, a second-order terminal sliding mode control law is proposed for airspeed and pith attitude control, which can guarantee robustness of the system. The overall flight control system is completed with the outer-loop altitude-hold control based on a PID controller. Simulation results show the good performance of the proposed control scheme.

nonlinear system; flight control; terminal sliding mode; second-order sliding mode

2016-03-26；

2016-04-29。

国家自然科学基金资助项目(61273141)；航空科学基金资助项目(20141396012)。

王文星(1985-)，男，陕西富平人，硕士，工程师，主要从事飞行力学、飞行仿真方向的研究。

孙秀霞(1962-)，女，山东潍坊人，教授，博士生导师，博士，主要从事现代鲁棒控制、飞行控制方向的研究。

1671-4598(2016)09-0107-03

10.16526/j.cnki.11-4762/tp.2016.09.029

V249.1

A