上证指数股价泡沫实证分析

刘 新，王福豪

(重庆理工大学 经济金融学院，重庆 400054)



上证指数股价泡沫实证分析

刘 新，王福豪

(重庆理工大学 经济金融学院，重庆 400054)

采用间接度量法，建立TAR模型和AR模型，运用协整理论剔除上证指数中的实际价格，以检验我国上证指数月度收盘均价的泡沫情况。实证结果表明：AR模型可以很好地拟合股价泡沫的演变路径，优于TAR模型。基于实证分析得出结论并且给出促进消费和协调银行体系与股市关系的建议。

间接度量法；协整理论；TAR模型；AR模型

一、前言

自2014年始，我国股市呈现牛市状态，上证指数逐步攀升，至2015年6月底增长了1倍多，之后开始出现大幅回落，起起伏伏的震荡现象再一次将“我国股市有没有泡沫，泡沫存在的程度有多大”的问题呈现在人们面前。在这种背景下，本文将对上证指数价格泡沫时间序列进行实证分析，以检验我国股市泡沫是否存在结构性断点，在此基础上提出控制股市泡沫的建议。

在市场经济交易活动中，某项资产产生价格泡沫的原因是市场价格与内在价值(实际价格)出现背离，当市场价格大于实际价格时为正向泡沫，反之为负向泡沫。由于在现实经济运行状况下，正向泡沫对一国或某一地区经济发展的影响远大于负向泡沫，所以人们把精力集中在正向泡沫的研究。在度量股票价格泡沫的过程中，关键一步是分离出实际价格。目前分离实际价格的方法有两种，即直接度量法和间接度量法。直接度量法是将未来股票价格和股利通过折现因子折现到当前的价格作为股票的实际价格。间接度量法是选取影响股票价格的几个重要经济变量决定其实际价格。从两种方法的本质分析，直接度量法更加合理精确，但是由于我国股票市场起步晚、发展历史短、未来股息分红少且股利不确定等综合因素，直接度量法的优势在我国股票价格度量方面不能充分发挥。根据历史经验，我国股票市场呈现明显的“齐涨共跌”现象，受到宏观经济变量影响很大。结合我国股票市场实际情况，本文即采用间接度量法剔除上证指数股票价格的实际价格。

二、文献综述

周爱民认为经济泡沫现象来源于理性预期条件下指标真实值与实际值之间的差值并可度量。度量的工具和方法分别是股市泡沫行为方程和判别是否存在收敛稳定解的非蓬齐对策条件[1]。在理性预期假定的基础上，周爱民讨论了检验股市泡沫的方法，并修正协整检验方法，结合上证指数泡沫现象实证分析，结果表明，希勒超长易变性方差比检验方法、修正协整检验方法和动态自回归检验方法可以互相印证[2]。

现有研究表明，股票价格时间序列往往呈现非线性特征。在分离出股票价格泡沫成分后，学者们提出非线性时间序列模型拟合泡沫成分的演变路径。Quandt于1958年提出马氏域变模型，并且得到Goldfeld和Hamilton的补充，进而使马氏域变模型逐步完善。尽管该模型发展较为成熟，但由于计算机技术的发展滞后，直到20世纪80年代末期才被广泛应用于经济学领域的实证分析。运用马氏域变模型，Cecchetti等对美国证券市场回报率进行实证研究，结果表明马氏域变模型具有很好的拟合性[3]。Nordon和Schaller对加拿大的股票泡沫进行检验，实证表明加拿大股票市场存在“有泡沫”和“无泡沫”两个状态，并且得到各个时点下的“有泡沫”状态下的概率[4]。孟庆斌等运用间接度量法得到上证指数价格泡沫，建立马氏域变模型确定沪市在每一时刻存在泡沫的概率，并结合深证指数分析沪深两市的泡沫联动性[5]。孟庆斌等在已有研究成果的基础上结合上证指数价格泡沫情况的实证分析，比较非齐次马氏域变模型与齐次马氏域变模型的建模效果，结果表明非齐次马氏域变模型得出的有泡沫概率和无泡沫概率可以更加精确详细刻画我国股市各个时段上的泡沫水平[6]。

随着金融衍生品不断涌现以及金融市场交易量空前增加，突发事件对金融时间序列的影响受到人们的格外关注。为了反映金融市场交易过程中的突变特征，学者们提出TAR模型。TAR模型称为门限自回归模型，属于AR自回归模型的变形，可以捕捉到时间序列的突变特征。Ahmed等建立TAR模型(Threshold Autoregressive,TAR)分析太平洋周围国家的股市价格泡沫情况[7]，Kelleher等同样建立TAR模型分析韩国股票市场股价泡沫的演变路径[8]，实证表明TAR模型因为考虑到突变结构提高了拟合效果。朱敏等提出不确定环境下MTAR模型的非常返性并推导出序列几何遍历的充分条件[9]。在前人研究成果的基础上，崔畅等将MTAR模型应用于我国股市投机性泡沫的研究，实证表明我国股票市场存在周期性破灭的投机泡沫[10]。孟庆斌等对经典股票价格泡沫模型予以推广，在随机利率背景下构造股价泡沫周期性破灭的理论框架，进而运用TAR模型对我国上证指数的价格泡沫情况进行检验，最终得出有益结论[11]。

基于马尔可夫区制转换方法和VNS模型，赵鹏等针对我国沪市周期性破灭型投机泡沫的存在性展开实证研究，得出上证指数月度超额收益率的变化可分为泡沫生存和泡沫破灭两个状态，沪市投机泡沫特征符合周期性破灭型投机泡沫[12]。张景齐利用直接度量方法对我国基于滚动投资的A股股市泡沫研究，结果表明：短期内股票价格围绕价值线上下波动，从长期来看企业的质量决定股市泡沫的大小程度[13]。高志结合上证指数历史数据，建立SOM神经网络与支持向量机方法构建泡沫临界点侦测模型，实证表明该模型可以识别上证指数泡沫状态转换临界点[14]。游家兴等利用转播学中“沉默的螺旋”理论对资产误定价构造综合评价指标进行研究，得出媒体情绪越高涨或者越低落资产价格就越容易偏离实际价格[15]。张勇以上市公司为样本验证稳健性会计信息披露对股价波动的影响，结果表明资产价值准备的正常计提促使股价上升，非正常计提造成股价泡沫[16]。邵新建等认为在IPO上市初期个体投资者越乐观，股价泡沫越大[17]。

从上述文献中总结出股市泡沫的检验方法有直接检验法和间接检验法。间接检验法依据股价的分布特征检验泡沫是否存在，比如周爱民设计多种间接法并对中国股市进行实证检验。直接检验法较多采用机制转换模型，主要有两类模型：一是门限自回归模型，比如崔畅和刘金全[10]；二是马氏域变模型，比如孟庆斌、赵鹏等[5-6，12]。在已有文献中，学者们大多运用马氏域变模型或者TAR模型度量分析股价泡沫情况，很少有学者将AR模型和TAR模型针对我国股票价格泡沫路径作比较。因此，本文将AR模型和TAR模型应用于我国股票市场做拟合优度比较实证分析。在协整理论基础上，利用间接度量方法剔除决定股票价格的理性成分(实际价格)，股票的真实价格与宏观经济变量决定的股价之差即为股票价格理性泡沫[11]。对上证指数价格泡沫分别建立AR和TAR模型，捕捉价格泡沫的非线性特征，分析其演变路径，探讨沪市交易过程中是否存在突变特征及其泡沫成分，得出不同的结论。

三、理论分析

在金融时间序列分析中，对于平稳的时间序列人们通常建立AR模型拟合其非线性演变特征[11]。通常情况下如果一个时间序列满足：

Yt=c+α1Yt-1+α2Yt-2+…+αpYt-p+ξ

(1)

则称时间序列{yt},t=1,2,…为AR(P)过程。随着我国市场经济的不断完善、改革开放进程的不断深入以及计算机和互联网技术的空前发展，我国股票市场也发生了重大变化，各种金融衍生品层出不穷、金融市场规模和金融交易频率空前扩张导致金融时间序列往往呈现结构性突变或跳跃现象。因此，为了拟合当前金融时间序列的非线性特征，学者们提出了TAR模型。一般情况下，如果时间序列{yt},t=1,2,…满足：

(2)

则称为一个k段门限自回归模型。其中zt-d为门限变量，是可测的。rj为门限值，k为正整数，是TAR模型的段数，ξ为服从独立同分布的随机白噪声序列。在实际研究过程中，人们经常采用Tong和Lim提出的TAR模型[18]，其一般形式可以表示为：

(3)

其中，α为阈值，是未知量，本文通过Chan提出的网格搜索法进行确定[19]。同时TAR模型也表明在金融时间序列中通过阈值将其分为若干部分，考虑到了金融时间序列的结构性突变或跳跃现象。

四、实证分析

(一)基于Johansen协整检验方法的股价泡沫分离

股票价格受到宏观经济形势相关变量影响有国民经济总体指标、投资指标、消费指标和金融指标[20]。国民经济总体指标一般用国内生产总值和工业增加值等衡量，投资指标一般用全社会固定资产投资额衡量，消费指标指社会消费品零售总额和城乡居民储蓄存款余额，金融指标一般用货币供应量、利率和汇率等衡量。为了直接反映银行体系对股市泡沫的影响，本文采用各项贷款指标。鉴于统计局网站没有公开工业增加值数据，本文选取制造业采购经理指数作为替代，选取广义货币与狭义货币之差(M2M1)、金融机构各项贷款总量(Loan)、消费者价格指数(CPI)、汇率(FE)和制造业采购经理指数(PMI)5个宏观经济变量作为解释变量，上证指数月度收盘均价(Shanghai Composite Index Monthly Closing Price,简称SCIMCP)作为被解释变量。所选数据的时间窗口为2006年1月到2015年5月。

在协整检验之前，为消除季节变动等因素的影响，本文对上证指数收盘均价、消费者价格指数、汇率、广狭义货币差和各项贷款做对数变换，并且对制造业采购经理指数等6个经济变量时间序列做X-11平滑处理并做协整回归，得出协整方程和协整残差即股价泡沫。对股价泡沫进行平稳性检验和自相关检验，如果股价泡沫序列没有通过两个检验的任何一个就说明协整残差中存在股价泡沫。对股价泡沫建立AR和TAR模型，辨别模型的拟合效果。如果AR模型拟合效果优于TAR模型则说明上证指数股价泡沫不存在结构断点或突变特征。根据协整回归结果以及AR和TAR模型的拟合股价泡沫的优劣差别得出结论并提出建议。

协整理论要求每个时间序列是非平稳的，因此本文对6个时间序列进行平稳性检验，结果如表1所示。

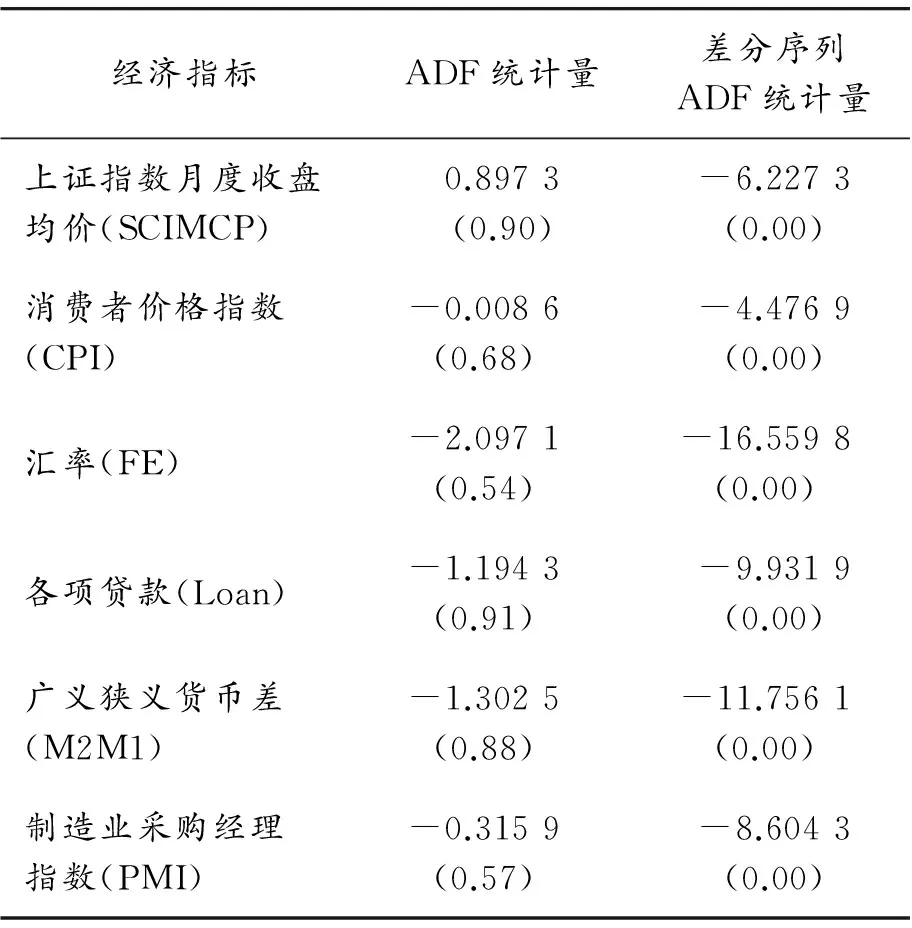
表1 各经济变量平稳性检验结果

注：括号中的值为ADF统计量概率p值。

通过对各经济变量进行平稳性检验得出各经济变量原序列都无法拒绝存在单位根的原假设，汇率的二阶差分序列以及其他5个变量的一阶差分序列在1%水平拒绝了存在单位根的假设，即汇率为I(2)过程，其他5个变量序列均为I(1)过程。为剔除股票价格的实际价格，本文对6个经济变量进行Johansen协整检验，结果如表2所示。从表2可以看出变量间在5%水平上存在两个协整关系。

表2 协整检验结果

Yt= -3.3587FE(-2)+ 2.9590LOAN(-1)-

(0.00) (0.00)

3.335 3M2M1(-1)+ 0.039 9PMI(-1)+

(0.00) (0.00)

3.690 5CPI(-1)

(4)

(0.00)

在协整检验基础上，建立回归模型定量分析经济变量之间的相互作用。协整方程结果如式(4)所示。括号内为对应系数的概率P值。从协整方程中，我们发现各项贷款总量、制造业采购经理指数和消费者物价指数的滞后一期时间序列与上证指数泡沫具有正相关关系，并且都在1%水平上显著，其中影响最大的是消费者物价指数的滞后一期，这与实际经济情况相符。在现实经济运行过程中，消费者物价指数增长会抑制消费，会有更多资金流入股市，进而使股价升高，这时往往是最容易出现股市泡沫的时刻。与之相反，汇率的滞后两期以及广狭义货币差的滞后一期对上证指数泡沫具有抑制作用，并且都在1%水平上显著。从二者的系数上分析，广狭义货币差和汇率对协整残差的抑制作用相当[21]。各项贷款总量、汇率和广狭义货币差都与银行体系息息相关，从而也表明银行体系对股市泡沫调节过程中的重要作用。然后对得到的股价泡沫序列进行平稳性检验和自相关检验，平稳性检验结果和自相关检验结果分别如表3和表4所示。

从表3可以看出，残差序列在5%水平上拒绝单位根假设，即残差序列是平稳的。然而从表4看出，经过自相关检验得出其概率P值均小于0.05，即残差序列存在自相关。本文对残差序列进行描述性统计，结果如表5所示。从表5可以看出，残差序列呈现略微左偏、高峰的现象，峰度值大于3，JB统计量的概率值很小，显然不服从正态分布。单位根检验和协整检验方法都是基于线性自回归过程，并且假设变量之间的均衡调整过程是对称的。残差序列的柱状分布如图1所示。单位根检验和协整检验方法都是基于线性自回归过程，并且假设变量之间的均衡调整过程是对称的。观察图1发现，残差序列的发展路径是非对称的，明显不符合线性特征。

表3 残差序列平稳性检验结果

表4 残差自相关检验结果

表5 残差序列的描述性统计结果

综合情况分析，导致残差序列出现自相关且不服从正态分布的原因是沪市存在价格泡沫，因此可以把残差序列认定为股价泡沫序列并且残差序列很可能存在结构性突变或结构性断点[22]。并且从图1可以看出在2006到2013年间该序列的波动是逐渐变小的，也就是说波峰和波谷的值逐渐变小；自此之后，波动幅度又逐渐变大。从2006年1月到2015年5月，股价泡沫序列的演变路径几乎是按照由负到正的规律交替变化的。值得注意的是，股价泡沫序列的演变路径在2008年6月由正转负，这主要是2008年金融危机爆发，股市泡沫骤然破灭所致。股价泡沫序列的非线性特征为本文构建AR和TAR模型提供了现实依据。

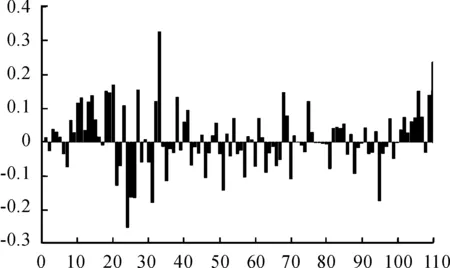
图1 残差序列分布图

(二)建立AR与TAR模型

经过试验，发现上证指数泡沫序列与其滞后一期和滞后两期有关。因此，首先对上证指数泡沫时间序列建立TAR(2)模型。在估计TAR模型的参数之前，利用chan方法在所有数据中搜索阈值，得到阈值α为0.197 7。在该阈值的作用下，将所有泡沫序列分为两部分，并分别估计方程参数。TAR模型的估计结果如式(5)所示。

(5)

为与TAR模型进行比较，本文建立AR模型。AR模型的参数估计结果为：

(6)

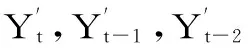
(7)

其中，Yt表示根据AR模型和TAR模型得到的预测值。MSE值越小说明模型拟合效果越好。利用Matlab软件实现得到，TAR模型的MSE值为0.236 2，AR模型的MSE为0.235 8。这说明AR模型的拟合效果优于TAR模型。同时这也说明在2006年至2015年上证指数不存在结构性断点或突变现象。

五、结论与建议

在实证分析过程中，本文选取了各项贷款总量、广狭义货币差和汇率3个与银行体系相关的宏观经济指标。结果表明：各项贷款总量滞后一期系数大于零，并且在1%置信水平上显著，显示其对股市泡沫的促进作用；广狭义货币差滞后一期系数和汇率滞后两期系数小于零，在1%置信水平上显著，显示其对股市泡沫的抑制作用。上述3个经济变量与股市泡沫时间序列的关系说明银行体系对股市价格泡沫有很大的影响。从实证分析结果来看，在控制泡沫水平的过程中，银行体系扮演了重要角色。历史经验告诉我们，由于银行资金过多参与股市交易，1929年美国经济出现大萧条和日本经济泡沫破灭后到目前为止其宏观经济运行状况仍不容乐观。在2008年金融危机中，由于美国没有控制好银行资金与股市的流动，导致美国金融机构竞相倒闭破产。然而，由于能够较好地控制银行资金与股市的关系，我国在调控宏观经济、应对金融危机过程中略显优势，在世界经济复苏进程中发挥了重要作用。虽然我国成功应对金融危机，但是历史经验为我们敲响警钟，银行体系与股市泡沫关系密切，因此银行体系对股市泡沫的调节作用不言而喻。

从实证结果分析，消费者物价指数对股价泡沫促进最大，也就是说，当物价处于较高水平时，人们放弃消费转而把闲散资金投入股市，无疑会促使泡沫的膨胀。因此，在股市出现大量泡沫时，相关部门可以采取刺激消费的措施以拉动真实需求，为股市泡沫釜底抽薪。当股市泡沫处于较高水平特别是股价脱离实体经济基本面出现持续快速单边上涨时，需要采取刺激消费政策，促进实体经济发展，而不能利用强制手段刺破泡沫，不然大量泡沫骤然破灭释放的负能量会对实体经济产生毁灭性打击。

此外，从AR和TAR模型对股市泡沫序列的拟合效果来看，AR模型更适合刻画我国股市泡沫的演变路径，其拟合优度比TAR模型更优，这种情况同时也表明我国股市不存在结构断点或突变特征。2008年我国股市之所以不存在结构性断点或突变特征，本文认为原因是中央政府启动了四万亿投资以及实行的“一揽子”货币政策。当时全球经济面临二战以来最为严重的大萧条，我国实体经济也受到极大打击，中央政府的四万亿投资极大促进了实体经济和股市的复苏。

本文建议在调节股市泡沫的过程中应注重银行体系的重要作用；当泡沫大量存在时政策重心应以促进消费为主，以促进实体经济发展。股价泡沫程度与宏观经济运行状况息息相关，受到宏观经济部门和投资者的重点关注。学界和民间对股价泡沫的观点也各不相同，本文认为允许适量泡沫可以促进宏观经济的良好发展。因此，把股价泡沫控制在适量水平是保护实体经济、促进宏观经济健康发展的重要环节。

[1] 周爱民.股市泡沫及其检验方法[J].经济科学，1998(5)：44-49.

[2] 周爱民，张雪莹.股市泡沫的理论与实证[J].世界经济，1999(10):10-14.

[3] CECCHETTI S G,LAM P，MARK N C.Mean reversion in equilibrium asset prices[J].American Economic Review,1990,80:398-418.

[4] NORDEN S,SCHALLER H.The predictability of stock market regime:evidence from the Tornoto Stock Exchange[J].Review of Economics and Statistics,1993(3):505-510.

[5] 孟庆斌，周爱民，汪孟海.基于齐次马氏域变方法的中国股市价格泡沫检验[J].金融研究，2008(8):105-118.

[6] 孟庆斌，靳晓婷，吴蕾.齐次及非齐次马氏域变模型在股价泡沫检验中的应用[J].数量经济技术经济研究，2011(4):124-137.

[7] AHMED E,ROSSER J B,UPPAL J Y.Evidence of nonlinear speculative bubbles in Pacific-Rim Stock Markets[J].The Quaterly Journal of Economics and Finance,1999,39:21-36.

[8] KELLEHER D,KIM G S,KIM S.Evidence of Bubbles in the Korean Stock Markets[C].Lugano:EFMA Meeting Proceedings,2001.

[9] 朱敏，俞政.随机环境下的MTAR模型的几何遍历性[J].数学理论与应用，2006，26(4):44-47.

[10]崔畅，刘金全.我国股市投机泡沫分析——基于非线性协调整关系的实证检验[J].财经科学，2006(11)：24-30.

[11]孟庆斌，周爱民，靳晓婷.基于TAR模型的中国股市价格泡沫检验[J].南开经济研究，2008(4):46-55.

[12]赵鹏，曾剑云.我国股市周期性破灭型投机泡沫实证研究——基于马尔可夫区制转换方法[J].金融研究，2008(4):174-187.

[13]张景齐.基于滚动投资的我国A股股市泡沫研究[J].山西财经大学学报，2013,35(1)：19-29.

[14]高志.基于神经网络和支持向量机的股价泡沫临界点识别模型[J].蚌埠学院学报，2014,3(1):65-68.

[15]游家兴，吴静.沉默的螺旋：媒体情绪与资产误定价[J].经济研究，2012(7):141-152.

[16]张勇.利用资产减值进行盈余管理对股价的影响[J].经济纵横，2011(12):110-113.

[17]邵新建，巫和懋，李泽广，等.中国IPO上市首日的超高换手率之谜[J].金融研究，2011(9)：122-137.

[18]TON H,LIM K S.Threshold autoregression,limit cycles and cyclical cata(with discussion of the paper)[J].Journal of the Royal Statistical Social Society,1980,42(3):245-292.

[19]CHAN K,MCQUEEN G,THORLEY S.Are there rational speculative bubbles in Asian stock market?[J].Pacific-Basin Finance Journal,1998(6):125-151.

[20]卜乐乐,姚佐文.我国宏观经济与证券市场关系的实证分析——基于名义GDP和上证指数发展速度的视角[J].重庆理工大学学报(社会科学)，2014(10)：59-64.

[21]邱冬阳,杜诗茗.IPO抑价存在星期效应吗?——基于深圳创业板的实证[J].重庆理工大学学报(社会科学)，2015(5)：38-46.

[22]孟庆斌.股市价格泡沫研究——泡沫度量及其影响因素分析[D].天津：南开大学，2009.

(责任编辑 魏艳君)

An Empirical Analysis of the Bubble of Shanghai Composite Index Stock Price

LIU Xin,WANG Fu-hao

(School of Economics & Finance, Chongqing University of Technology, Chongqing 400054, China)

This paper aims to test the bubble of the monthly closing price of the Shanghai Composite Index with co-integration theory by using the indirect measurement method and building the TAR model and AR model. The empirical result show that AR model can well fit the evolution path of stock price bubble, and it is better than TAR model. Based on the empirical analysis, we make the conclusion and put forward suggestions for promoting consumption and coordinating the relationship between the banking system and the stock market.

indirect measurement method；co-integration theory；TAR model；AR model

2015-12-10

刘新(1970—)，女，重庆人，教授，博士，研究方向：微观金融、财政学。

刘新,王福豪.上证指数股价泡沫实证分析[J].重庆理工大学学报(社会科学)，2016(10):60-66.

format：LIU Xin,WANG Fu-hao.An Empirical Analysis of the Bubble of Shanghai Composite Index Stock Price[J].Journal of Chongqing University of Technology(Social Science)，2016(10):60-66.

10.3969/j.issn.1674-8425(s).2016.10.009

F832.5

A

1674-8425(2016)10-0060-07