二叉树从二期模型到n期模型的扩展

冯晶晶，樊亚云，邢瑞芳

(西安培华学院 通识教育中心，西安 710125)



二叉树从二期模型到n期模型的扩展

冯晶晶，樊亚云，邢瑞芳

(西安培华学院 通识教育中心，西安 710125)

介绍期权定价的离散模型—二叉树模型。通过讨论期权定价的一期模型，得到一期模型的期权定价公式及其性质。在此基础上，讨论了期权定价的二期模型,最后由期权定价的二期模型推广到n期二叉树模型。

期权；二叉树模型；一期模型；二期模型；n期模型

金融数学[1-2]是应用数学的一个分支，是运用数学的方法解决实际操作中的金融问题，进行数学建模[3]、数据分析[4]、数值计算[5]等定量分析，以找到金融学的内在规律并指导实践。数学模型对金融市场中的交易者起非常大的作用，证券组合投资模型和金融衍生工具定价模型的出现是数学模型应用于金融市场研究的标志，资本资产定价模型是由此发展起来的具有重大应用价值的金融数学模型[6]。期权[7]是主要的金融衍生产品，是金融工程的主要工具，也是构成金融工程其他金融衍生品的基础。文献[8]讨论了期权价格及其定价模型。本文讨论了期权定价的离散型模型—二叉树模型。但由于期权定价的一期模型过于简化，只包括一支随机变化的股票和一种现金债券，并且在单个时间段末股价变化只有2种可能值，并且金融市场又是十分复杂的，所以本文讨论期权定价的n期二叉树模型，以适用于更复杂的金融市场。

1　预备知识

二叉树期权定价模型：设资本市场是竞争的，且不存在交易费用、税收，不存在无风险套利机会，股票和期权是无限可分的，那么股票在下一期的价格仅有2种可能，如图1所示，其中，ru>1+r>d>0，r为无风险利率。

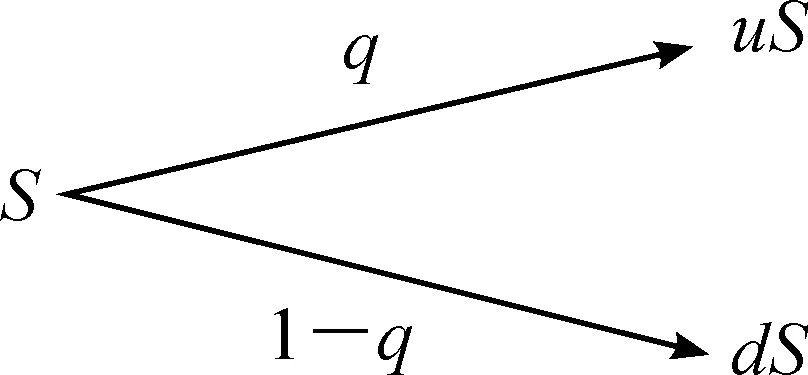
图1　股票下一期的价格

假设以该股票为标的看涨期权的价格为C，执行价格为X，则看涨期权的价值变化如图2所示。

图2　看涨期权的价值变化

为解决期权定价问题，需构造一个无风险套期保值的证券组合：购买一份股票，卖掉m份期权，如图3所示。

图3　一个无风险套期保值的证券组合

因证券组合是无风险证券组合，故有(1+r)(S-mC)=uS-mCu，所以

(1)

将m代入式(1)得

(2)

令

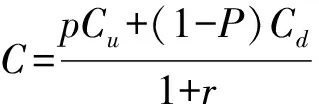
2　二期模型到n期模型的扩展

为了得到n期期权价格公式，首先讨论二期模型。设二期模型的无风险利率也为r，且每期复利一次，股票的初始价格为S，在二期末到期的看涨期权的执行价为X，如图4所示。以该股票为标的二期看涨期权的价值如图5所示。则

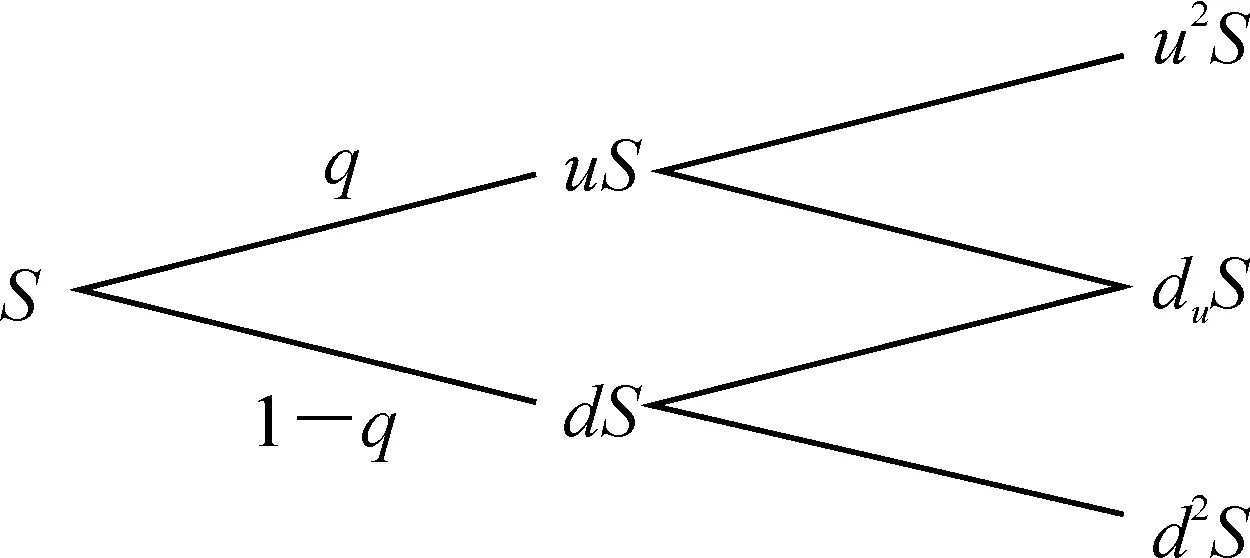
图4　二期模型

图5　二期看涨期权的价值

类似于期权定价一期模型，为了得到期权的价格，需要构造无风险套期保值证券组合，从而有

(3)

将Cu，Cd代入式(3)得

(4)

可以看出：式(4)是由两次应用一期模型定价公式得到的，分子是(pCu+(1-p)Cd)2的二项式，且CuCu，CuCd，CdCu，CdCd分别用Cuu，Cud，Cdd代替，则有

设股票的初始价格为S，期限为n期，其变化规律与期权定价的二期模型相同，其他参数不变。股票价格的n次波动相当于试验次数为n的二项试验，则n期欧式看涨期权取值的分布如表1所示，所以

(5)

(6)

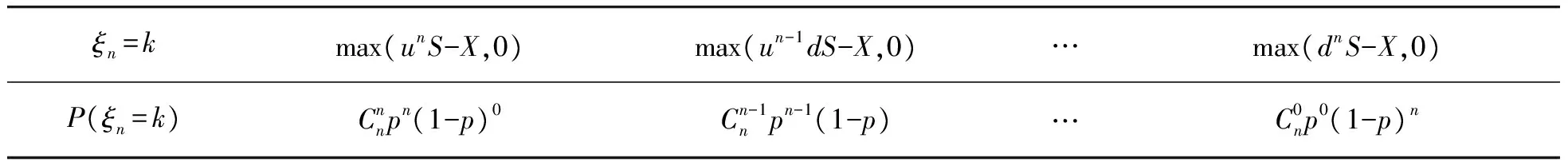
表1　n期欧式看涨期权取值的分布

在n期模型中，股票价格上涨的次数ξn≥a与下降次数ξn

因此，欧式看涨期权二项式定价模型可化为

3　结束语

期权定价模型从一期模型推广到n期二叉树模型，看涨期权的价格随股票价格的上涨而上涨。当执行价格升高时，看涨期权价格随之下降。当无风险利率上升时，影响执行价格的折现值，从而使看涨期权的价格上涨。期权到期期限n也使得看涨期权价格上涨，同时二项分布的方差也影响看涨期权的价值。

[1]斯塔夫里.金融数学[M].蔡明超，译.北京：机械工业出版社，2004:1-18.

[2]王小群．金融数学介绍[J].系统工程，1999(6)：111-114．

[3]陈光亭，裘哲勇．数学建模[M].北京：高等教育出版社，2010:34-105.

[4]蔡瑞胸．金融数据分析导论[M].北京：机械工业出版社，2013:1-72．

[5]魏毅强，张建国，张洪斌，等.数值计算方法[M].北京：科学出版社，2004:112-177．

[6]夏玉森，汪寿阳，邓小铁.金融数学模型[J].中国管理科学，1998,6(1)：1-9.

[7]郁洪良.金融期权与实物期权[M].上海：上海财经大学出版社，2003:8-43.

[8]王乐毅，朱伟，刘伟.期权价格及定价模型分析[J].贵州工业大学学报，2006,8(2)：46-48.

[9]赵彦辉．概率论与数理统计[M].西安：西北大学出版社，2014：32-38．

(责任编辑刘舸)

Extension of Binomial Model from Two-Period Model ton-Period Model

FENG Jing-jing, FAN Ya-yun, XING Rui-fang

(Center of General Education, Xi’an Peihua University, Xi’an 710125, China)

A discrete model of option pricing, which is a Binomial model, was introduced. One-period model of option pricing was discussed, and the option pricing formula and its properties of the one-period model were given. On the basis of it, the two-period model of option pricing were discussed. Finally, the two-period model of option pricing was extended ton-period model.

option; binomial model; one-period model; two-period model;n-period model

2016-05-18

陕西省自然科学基金资助项目(2007A12)；陕西省教育厅专项科学研究资助项目(2015JK2093)；西安培华学院科研基金资助项目“多因子远期利率期限结构模型”(PHKT16028)

冯晶晶(1984—)，女，陕西韩城人，硕士，讲师，主要从事应用数学研究，E-mail:fengjingjing0105@163.com。

format：FENG Jing-jing, FAN Ya-yun, XING Rui-fang.Extension of Binomial Model from Two-Period Model ton-Period Model[J].Journal of Chongqing University of Technology(Natural Science)，2016(10):181-184.

10.3969/j.issn.1674-8425(z).2016.10.029

O29; F224

A

1674-8425(2016)10-0181-04

引用格式：冯晶晶，樊亚云，邢瑞芳.二叉树从二期模型到n期模型的扩展[J].重庆理工大学学报(自然科学)，2016(10):181-184.