锅筒径向温差及其引起的热应力计算方法探讨

袁继禹，沈火明

(1.西南交通大学 力学与工程学院，成都 610031;2.东方电气集团东方锅炉股份有限公司，成都 611731)



锅筒径向温差及其引起的热应力计算方法探讨

袁继禹1，2，沈火明1

(1.西南交通大学 力学与工程学院，成都 610031;2.东方电气集团东方锅炉股份有限公司，成都 611731)

采用GB/T 16507—2013的计算公式和有限元方法分别对锅筒在启动过程中的径向温差及其引起的热应力进行了分析。结果表明：在温度变化速率保持稳定的情况下，标准公式与有限元方法的计算结果吻合较好。

锅筒；温差；热应力；有限元方法

随着电力工业的发展，人们对电站锅炉的运行寿命越来越重视。锅炉中有大量的承压部件，这些部件不仅承受着很高的压力和温度，而且在运行过程中还要伴随压力、温度的不断变化。温度和压力的变化使得结构上产生交变应力，频繁的交变应力将会使金属材料的疲劳损伤增大，缩短锅炉的运行寿命，给电站锅炉的运行和电力生产带来安全隐患。

锅筒作为锅炉中关键部件之一，也是典型的承受着较大交变载荷的结构。计算锅筒的疲劳寿命的过程是：先计算锅筒在运行期间的应力幅，然后根据应力幅查取S-N曲线，根据相关数据进行寿命评估。锅筒的应力主要包括两部分：一是内压及其他机械载荷引起的应力；二是锅筒结构上的温差引起的热应力。热应力是影响锅筒疲劳寿命的关键因素之一，锅筒结构壁厚较大，内外壁温差(径向温差)和上下壁温差(周向温差)是热应力产生的主要原因。国内学者对锅炉瞬态热应力进行了较多的研究。曾凡林等人[1]对锅筒在启、停过程中的热应力进行了计算，并采用有关规范对锅筒寿命损耗进行了计算。刘洪宪等[2]采用有限元方法对锅炉启动过程中的瞬态热应力进行了计算。李厚毅[3]对调峰机组锅筒低周疲劳寿命计算方法进行了研究。孟祥贵等[4]研究了厚壁圆筒热应力问题的传递函数方法。段鹏等[5]基于试验和有限元法对锅炉汽包低周疲劳损耗寿命进行了分析。

本文分别采用GB/T 16507.4—2013《受压元件强度计算》附录A《锅筒低周疲劳寿命计算》(以下简称GB/T 16507)中的公式和有限元程序ANSYS对锅筒的径向温差及其引起的热应力进行了分析，并对采用两种方法得出的计算结果进行了对比。

1　径向温差及其引起的热应力计算方法

1.1温度场分析理论

三维瞬态温度场在直角坐标中的微分方程[6]为

(1)

其中：ρ为材料密度；c为材料比热；t为时间；θ为温度；kx，ky，kz为材料沿x，y，z方向的热传导系数；qV为物体内的热源密度。

边界条件：

2) 边界上给定热流量q(第二类边界条件)，由傅里叶定律得：

其中，nx，xy，nz为边界外法线的方向余弦。

3) 边界上给定对流换热条件(第三类边界条件)，由牛顿冷却定律得：

其中：h为对流换热系数；θa在自然对流条件下为环境温度，在强迫对流条件下为边界层的绝热壁温度。

对于稳态温度场分析，微分方程等式右边为0。

1.2GB/T 16507中的径向温差及热应力计算方法

GB/T 16507中计算锅筒筒体径向内外壁温差的公式为[7]：

(2)

GB/T 16507中，径向温差引起的热应力公式为

(3)

其中：K2n为径向温差引起的环向热应力指数，其值为开孔处的热应力与无孔筒体内壁热应力理论解的比值；α为材料线膨胀系数；Cf为结构系数，与内、外径相关；μ为泊松比；E为弹性模量。该公式是根据热弹性理论和准稳态温度场简化推导得出。

1.3有限元瞬态温度场分析及热应力分析

有限元方法是将连续结构进行离散化的近似求解方法，最早应用于结构力学问题的求解中。随着计算机科学技术的进步和有限元计算方法的快速发展，有限元方法已拓展到结构力学、流场、传热学、电磁场、声学等多个领域[8-14]。采用有限元软件可以高效、准确地进行结构三维温度场分析。

与结构分析类似，温度场分析在有限元分析中同样可以描述为矩阵表达式，根据能量守恒原理，瞬态热平衡可以表达为[6]

(4)

采用有限元方法可以计算锅筒每个位置的温度随时间变化的过程，只要确定了锅筒介质(或内壁)温度的时间变化规律，就可以准确地分析锅筒在整个温度变化过程中的内外壁温差，根据瞬态温度场分析结果进一步分析，可以得出锅筒的热应力。

2　锅筒温度场及热应力计算

以下分别采用GB/T 16507计算方法和有限元分析对锅筒筒体结构径向温差及其引起的热应力进行分析。锅筒规格为φ2 070×135 mm，材料为BHW35，为便于计算，暂不考虑材料属性随温度变化，取弹性模量为2×105MPa，线膨胀系数为1×10-5，材料比热为578 J/(kg·K)，热导率为38.9 W/(m·K),密度为7.85×103kg/m3。

某工程锅筒启动曲线如图1所示。

图1　介质温度随时间变化曲线(启动曲线)

介质温度由启动初期A点到达稳定阶段B点经历时间为64 min，温度由21℃升至332℃。

2.1采用GB/T 16507中的公式计算径向温差及热应力

按准稳态考虑，锅筒介质温度由A点升至B点的速率为4.86 ℃/min，以该速率变化的时长为64 min。根据GB/T 16507中的图A.3和图A.4查得各系数，并将结构尺寸和材料属性等参数代入式(2)，可计算得该锅筒筒体的径向温差(见表1)。

表1　锅筒筒体径向温差计算

不考虑开孔等因素的影响， 即径向温差引起的热应力指数取1。将以上计算得到径向温差代入式(3)中，即可得到由径向温差引起的热应力(见表2)。

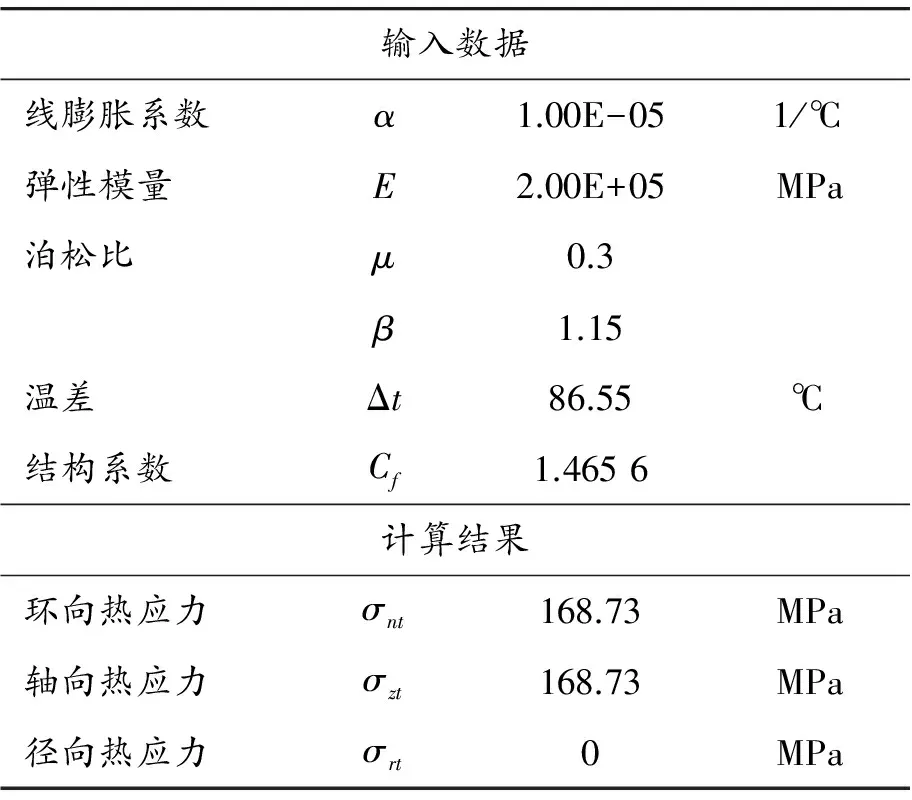
表2　径向温差引起的筒体热应力

2.2有限元分析

用ANSYS Workbench 14.0的瞬态热分析模块对结构进行准稳态(固定升温速率)和瞬态(温度按启动曲线变化)温度场分析(这里的“准稳态”仅仅是为了与按真实升温速率计算的瞬态分析过程进行区分，实际上也是对结构进行瞬态温度场分析的过程)，并根据温度场分析结果，采用静力分析模块对结构在径向温差作用下的热应力进行了线性静力分析。计算中假设外壁为绝热边界，且内壁温度与介质温度相等。

筒体温度场分布如图2所示。在升温过程中，内壁温度始终大于外壁温度。温度沿筒体厚度方向呈非线性分布，温度中性层不在1/2厚度处，其位置偏向内壁侧。

图2　温度沿径向分布图

径向温差作用下，最大热应力发生在温差最大的时刻，该时刻筒体Von Mises等效热应力分布如图3所示(图中仅示筒体1/2)，各单向热应力分布如图4所示。

图3　筒体Von Mises等效热应力分布

图4　径向温差引起的热应力分布云图

升温过程中，在径向温差作用下，环向热应力和轴向热应力分布和数值基本一致，均为内壁受压、外壁受拉,径向热应力很小，最大值仅为5 MPa左右。

筒体一端约束了轴向位移，在未约束的一端发生向外翘曲，这是由于高温区(内壁)热膨胀量大于低温区(外壁)，在变形协调的作用下，在自由端产生了附加弯矩。

图5　温度、热应力随时间变化曲线(ANSYS瞬态分析结果)

ANSYS瞬态分析中，启动曲线上升温速率最快的时间段为15～35 min，温差、热应力最大值均出现在启动后40 min时刻(见图5中竖直虚线对应处)，温差最大值与升温速率最快时刻有一定的滞后，这与金属材料的散热速率(k/(cρ))有关，散热速率越快，温差和热应力最大值出现的时间与升温速率最快时间之间的滞后时间越短。

ANSYS准稳态分析与瞬态分析都采用的是瞬态热分析模块，唯一区别在于输入温度(内壁温度)随时间变化规律有差别。从图1可以看出，启动曲线中升温阶段比较平滑，按照准稳态计算与直接输入启动曲线之间差别较小。计算结果显示：准稳态分析的温度场及热应力分布规律与瞬态分析相似，仅仅是最大温差(热应力)的发生时刻和数值不同。

2.3GB/T 16507与有限元分析结果比较

以上分别采用GB/T 16507计算公式、准稳态ANSYS分析、瞬态ANSYS分析3种方法对锅筒筒体的径向温差及其引起的热应力进行了分析。

图6显示了3种计算方法得出的温差随时间的变化曲线。由于GB/T 16507和ANSYS准稳态对升温速率进行了假设，计算得到的温差随时间变化的曲线除了查看最大温差外不具有实际意义。ANSYS瞬态温度场分析的结果曲线更能真实地反映结构在温度变化过程中温差随时间的变化情况。

图6　3种方法的径向温差随时间变化曲线

表3给出了采用3种计算方法得到的温差、热应力的结果对比。从表中可以看出：3种方法计算结果基本吻合，GB/T 16507的计算数值最小，ANSYS瞬态分析的计算数值最大；3种方法得出的径向温差和热应力误差不超过4%。GB/T 16507中未给出筒体外壁应力计算公式，且径向温差引起的径向应力(标准中称为法向应力)为0。ANSYS计算可以得到结构上任意一点的温度和热应力，从分析结果可以看出，结构中的径向热应力并不为0，由于热膨胀引起壁厚方向的弯曲，壁厚方向两侧对内部产生挤压，径向方向存在一定的压应力。

表3　3种方法计算温差和热应力数值对比

图7是ANSYS准稳态分析和瞬态分析中的环向热应力结果对比。由图中可以看出：内、外壁热应力呈非对称分布，内壁应力要大于外壁应力，这是由沿壁厚方向的温度非线性分布规律决定的。

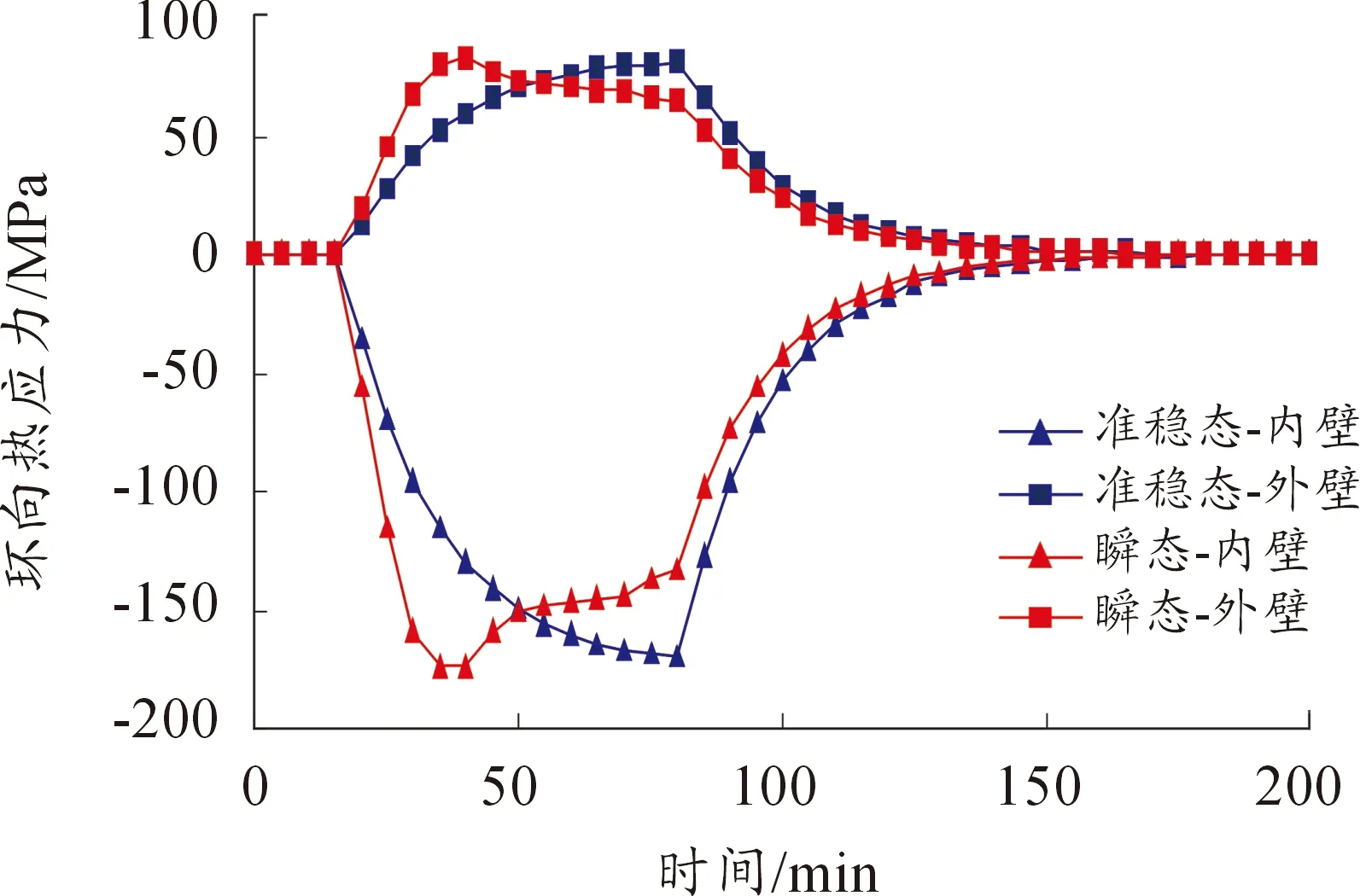
图7　准稳态和瞬态环向热应力对比

3　结束语

采用GB/T 16507的公式和有限元方法均可以对锅筒径向温差和热应力进行计算，在准稳态情况下，GB/T 16507和有限元计算结果吻合较好。温度变化速率对径向温差起决定性作用，GB/T 16507 的公式适用于温度变化速率波动较小的情况，在温度变化速率有较大波动时，采用 GB/T 16507 的公式计算会引起较大的误差。有限元计算方法可以对温度任意变化的情况进行计算，并且可以计算结构上任意部位的温度和应力结果，其计算结果更符合实际，更能满足工程设计的要求。

[1]曾凡林,林洪书.锅炉汽包的热应力及其寿命分析[J].东方锅炉，1994(2)：13-21.

[2]刘洪宪，金一.锅炉启动瞬态应力场有限元计算[J].东北电力大学学报，2010，30(6)：4-9.

[3]李厚毅.调峰锅筒低周疲劳寿命计算方法[J].东锅技术通讯，1982(2)：1-8.

[4]孟祥贵,陈棣湘,潘孟春.厚壁圆筒热应力问题的传递函数方法[J].强度与环境，2008，35(1)：40-46.

[5]段鹏,周新雅,杨菁，等.锅炉汽包复杂应力状态及低周疲劳寿命研究[J].热力发电，2010，39(8)：28-32.

[6]陈火红.Marc 有限元实例分析教程[M].北京：机械工业出版社，2002：342-350.

[7]GB/T16507—2013《水管锅炉》[S].北京：中国标准出版社，2014：110-116.

[8]程林风,王敏毅,黄朝学.基于ANSYS的舰载电子机柜振动可靠性研究[J].四川兵工学报,2014,35(1):115-118.

[9]闫淑梅,盛姣.仿真软件ANSYS 15.0在电子材料研制中的应用[J].电子元件与材料,2014,33(3):95-96.

[10]律辉,王优强,刘昺丽,等.基于Ansys的空心板条艉轴承力学性能分析[J].润滑与密封,2015(4):34-39.

[11]四库,陈盛贵,钟欢欢.激光透射焊接聚碳酸酯的有限元数值模拟[J].激光杂志,2015(6):104-107.

[12]冯海全,张瑞敏,韩青松,等.血管内支架的疲劳强度的有限元模拟分析[J].功能材料,2014(14):14087-14091.

[13]牛坡,杨玲,张引航,等.基于ANSYS Workbench的微耕机用旋耕弯刀有限元分析[J].西南大学学报(自然科学版),2015,37(12):162-167.

[14]刘昌奇,徐余法,李全峰,等.基于有限元分析的一种超超高效异步电机[J].电机与控制应用,2015(5):75-80.

(责任编辑刘舸)

Calculation Method of Radial Temperature Difference and Thermal Stress of Boiler Drum

YUAN Ji-yu1, 2, SHEN Huo-ming1

(1.School of Mechanics and Engineering, Southwest Jiaotong University,Chengdu 610031, China；2. Dongfang Boiler Group Co., Ltd., Chengdu 611731, China)

The formula of GB/T 16507—2013 and the finite element method were used to calculate the radial temperature difference and the thermal stress caused by the steam drum in the starting process, respectively. The results show that in the case of keeping the temperature change rate, the standard formula and the finite element method are in good agreement.

steam drum; difference in temperature; thermal stress; finite element method

2016-07-28

国家科技支撑计划资助项目(2011BAC05B01)

袁继禹(1985—)，男，硕士研究生，主要从事锅炉、压力容器力学分析方面的研究，E-mail:yzb239@163.com。

format：YUAN Ji-yu, SHEN Huo-ming.Calculation Method of Radial Temperature Difference and Thermal Stress of Boiler Drum[J].Journal of Chongqing University of Technology(Natural Science)，2016(10):55-60.

10.3969/j.issn.1674-8425(z).2016.10.008

TK223.1

A

1674-8425(2016)10-0055-06

引用格式：袁继禹，沈火明.锅筒径向温差及其引起的热应力计算方法探讨[J].重庆理工大学学报(自然科学)，2016(10):55-60.