GPS网共模误差的空间响应分析

龚国栋 贺小星,3 花向红,2 舒 颖 丁凌航

1 武汉大学测绘学院，武汉市珞喻路129号，430079 2 武汉大学灾害监测与防治研究中心，武汉市珞喻路129号，430079 3 华东交通大学土木建筑学院，南昌市双港东大街808号，330013



GPS网共模误差的空间响应分析

龚国栋1贺小星1,3花向红1,2舒 颖1丁凌航1

1 武汉大学测绘学院，武汉市珞喻路129号，430079 2 武汉大学灾害监测与防治研究中心，武汉市珞喻路129号，430079 3 华东交通大学土木建筑学院，南昌市双港东大街808号，330013

对共模误差的空间变化进行分析。以美国南加州及周边区域的GPS台站网中3个站台为中心，通过划分9个不同的尺度空间，采用基于主成分分析(PCA)的空间滤波方法，对每个空间尺度GPS坐标序列共模误差进行提取，探讨不同空间尺度下GPS网共模误差的空间响应特性，为子区域的划分提供相应的理论基础。

GPS坐标时间序列；共模误差；PCA空间滤波；空间尺度

共模误差(common mode error，CME)是GPS时间序列数据误差的主要来源之一，极大地影响GPS解的精度与可靠性[1-2]。为了准确地提取CME，国内外学者作了一些研究工作。斯克里普斯轨道与永久阵列中心(Scripps orbit and permanent array center，SOPAC)将整个GPS观测网(板块边界观测网plate boundary observation，PBO)划分为若干个子区域，再对各子区分别进行滤波。但该方法存在一定的局限性，对如何进行子区域的划分，不同的区域划分是否存在差异，没有进行深入的分析探讨[3]。另外，有学者指出共模误差在空间上不是等值的，即共模误差的空间响应并不是完全一致的[4]。考虑到CME的物理起源尚不明了，同时目前对其时空响应机制缺乏深入的研究，使得CME的分离存在一定的局限性，尤其是在大尺度范围的GPS网中，给准确、可靠地分离出CME造成了一定的困难。本文针对共模误差分离方法中存在的上述问题，以美国南加州及周边区域的一个GPS网为例，采用主成分分析的空间滤波方法，通过对不同尺度下的GPS网进行共模误差分离处理，分析共模误差的空间分布特性，探讨共模误差空间响应机制及其最佳分离策略。

1 GPS时间序列获取及其模型

为了研究不同尺度下共模误差的时空变化，本文选取了ITRF2008框架下美国南加州及周边区域的一个GPS网为例，分析不同尺度下共模误差的空间分布及其变化规律。以3个GPS站(BEMT，PIN1，MONP)为中心，通过控制GPS网的尺度，不断增加GPS网的大小，使其从小区域网逐渐扩展到大尺度的网形，根据距离划分多尺度GPS网区域，最大尺度的GPS网包含39个站，其站点分布见图1。通过对台站的时间序列进行处理，对不同尺度下的GPS网的共模误差空间变化进行探讨。

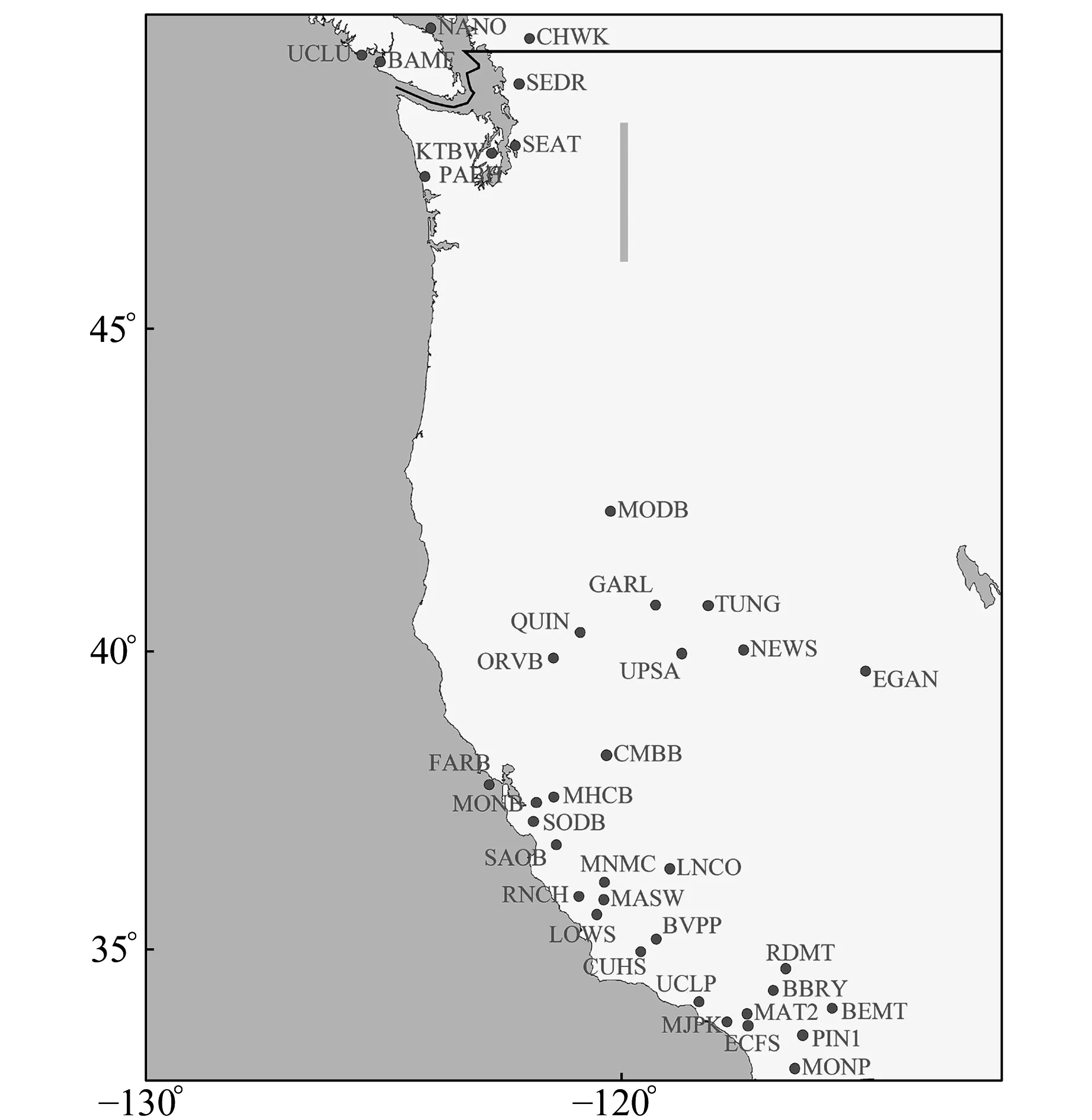
图1 GPS网站点分布Fig.1 Distribution of GPS satellites

通过对图1中GPS站2001～2006年的连续观测数据进行计算处理与分析，GPS坐标时间序列获取步骤如下[5]：

1)首先采用GAMIT软件对站点的原始观测数据进行处理，选取的站点数据时间跨度为2001～2006年，数据要求观测时间大于2.5 a，数据缺失程度小(本文数据平均缺失的比率为1.46%)。以每天24 h观测数据为基本单位，解算出各站点的三维坐标及其相关参数，形成单天解。

2) 在统一的基准下(ITRF2008)，结合SOPAC的单天解序列(GIPSY解算结果)，通过公共站点和卫星，采用QOCA[6](quasi-observation combination analysis)软件对单天解进行联合解算(GAMIT与GIPSY的权比为1∶2∶4)，获得台站网的坐标及其速度解等参数，得到GPS坐标时间序列。在QOCA软件进行联合平差过程中，给出三坐标分量方向(E、N、U)的残差限制值分别为30 mm、30 mm、100 mm。一旦观测值的残差超过这个值，就认为是过于弱的观测，予以剔除[6]。解算后的GPS原始坐标时间序列见图2a(限于篇幅，以PIN1站点为例)。

已有的研究表明，GPS单站、单分量位置间序列通常满足模型[7-9]:

y(ti)=a+bti+csin(2πti)+dcos(2πti)+

esin(4πti)+fcos(4πti)+

(1)

式中，ti(i=1,…,n)为GPS站点单日历元，以a为单位；a为站点位置(为序列的平均值)；b为线速度；c、d和e、f分别为年周期和半年周期项的系数；g为发生在历元Tg处的由于各种原因引起的阶跃(或称偏移)；H为Heaviside阶梯函数，这里假定发生偏移的时刻Tg已知；τj为粘滞系数。根据上述经典模型对GPS时间序列建立模型，以便对时间序列进行后续分析。

2 PCA空间滤波方法

为了评估共模误差对GPS坐标残差时间序列的影响，采用空间滤波改正前后GPS时间序列的加权均方根(weighted root mean square，WRMS)进行比较[10]。若空间滤波后GPS坐标残差时间序列WRMS减小，即表明非线性变化幅度减弱。

2.1 区域滤波数学模型

假设共模误差在某一区域均匀分布，将单日解误差作为权重因子[9]，区域叠加滤波法的共模误差分量εi可以表示为：

(2)

式中，εi为第i个台站的共模误差值；v为残差坐标时间序列；δi,j为单日坐标解得的残差；j为参与计算共模误差的台站数。

2.2 PCA数学模型

本文以GPS台站的时间序列为例，各台站的时间序列排列起来形成一个n×m(n>m，n为观测数或历元数，m为观测类型)的数据矩阵X，其协方差阵为CX，则CX=XTX。数据矩阵如下：

(3)

(4)

作如下定义：

(5)

(6)

(7)

(8)

(9)

令Λ=ΣTΣ，则有：

CX=XTX=(UΣVT)TUΣVT=VΛVT

(10)

即V构成X的正交基底。矩阵X按照KLE展开可得:

(11)

ak(ti)可由下式求出：

X=AV⟹A=XV-1⟹A=XVT

(12)

(13)

式中,ak(t)是第k个主成分，vk(x)是对应主成分的响应特征向量，分别代表时间特征和空间响应。

3 GPS时间序列算例分析

原始序列中包含着速度项、阶跃(offset)等非构造信号，往往需要对其进行去趋势、去周期项等处理。通过对单日解观测时间序列建立时间序列模型，对原始时间序列去除速度项、阶跃、指数和对数衰减等项，最后得到残差时间序列如图2(b)。从图2可知，台站残差序列波动比较大，坐标分量中误差相对较大，且坐标序列存在周期性波动趋势，在U方向(垂向分量)尤为明显。这说明GPS残差时间序列中存在与时间相关的噪声；从图3对应的剩余频谱图可知，在低频处的谱能量较大，频谱呈倾斜(斜率趋近于-1～0之间)，说明噪声中包含着有色噪声。

图2 站台PIN1Fig.2 GPS satellite site PIN1

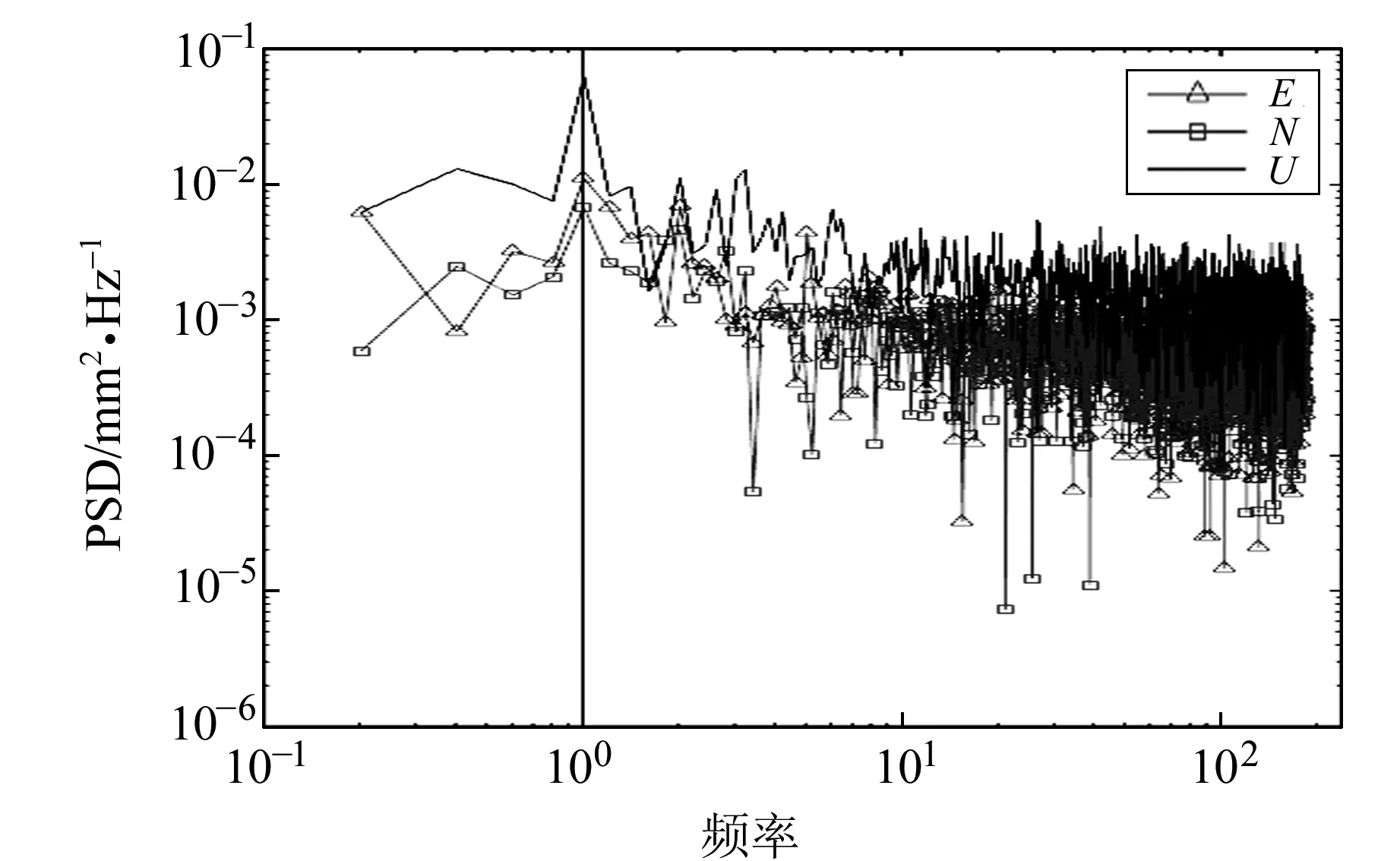
图3 PIN1站残差序列频谱图Fig.3 PIN1 station residuals spectrum

本案例以图1GPS台站网中3个站台(BEMT，PIN1，MONP)为中心，划分9个尺度空间(空间尺度分别为100km、200km、420km、550km、660km、810km、1 000km、1 660km、2 000km)，GPS时间序列处理过程中采用相同的处理策略，然后对残差序列采取主成分分析(PCA)的空间滤波方法对共模误差进行分离。PCA滤波后各GPS台站的残差坐标时间序列(以200km区域网中PIN1站点为例)如图2(c)。对GPS残差时间序列进行PCA主分量分离之前，考虑到环境负载会对GPS坐标时间序列WRMS产生影响，本文通过采用mload程序对GPS站作负载改正，对大气、积雪和土壤水、海洋非潮汐4项负荷效应进行负载改正，最后分别对不同尺度下的GPS网进行处理，滤波处理过程中选取PCA的前4个分量进行空间滤波。

图4表明，空间滤波前BEMT、PIN1、MONP3个站点E方向的WRMS分别为1.665mm、2.468mm、1.966mm；N方向的WRMS分别为1.233mm、1.532mm、1.381mm；U方向的WRMS分别为4.213mm、5.795mm、4.544mm。滤波后的WRMS-距离曲线显示，WRMS值总体上随距离的增加而增加，表明随着距离增加台站之间相互关系减弱，大尺度空间的共模误差更加难以提取处理。在距离小于420km时共模误差的滤波效果较明显，在这个区间中随着距离的增加，WRMS的增加明显，曲线斜率大，到达420km～600km区间的时候WRMS的增加变缓慢。距离在大于600km区间时E方向和N方向的WRMS几乎不再变化，1 000km距离以后U方向的WRMS也不再变化。空间滤波后在100km尺度空间上提取效果最好，BEMT、PIN1、MONP3个站点E、N、U方向的WRMS减少最明显，E方向WRMS减少分别为39.7%、93.2%、71.8%；N方向WRMS减少分别为40.2%、97%、61.3%；E方向WRMS减少分别为56.3%、86.4%、37.4%。图4中各条曲线超过420km后WRMS的曲线斜率基本不再发生变化，且滤波效果较差。根据这一曲线的变化趋势，笔者选取200km、420km、600km、1 000km这4个区域的所有测站进行研究。

图4 BEMT、PIN1、MONP滤波前后WRMS-距离曲线Fig.4 BEMT, PIN1, MONP WRMS- distance curve before and after the filter

表1说明，在200km空间尺度下区域滤波后，各站点在E、N、U 3个坐标分量上WRMS平均减少百分比分别为49.89%、47.64%、42.92%；时间序列残差的WRMS平均值减少0.982mm、0.792mm、1.973mm。表2说明了400km空间尺度下区域滤波以后各站点在N、E、U 3个方向上的加权均方根均有减少。图5(a)、5(b)、5(c)WRMS减少百分比曲线表明，在E、N、U 3个 坐标分量上WRMS平均减少约44.51%、39.72%、37.05%。

表1 200 km区域空间滤波前后残差坐标时间序列WRMS对比

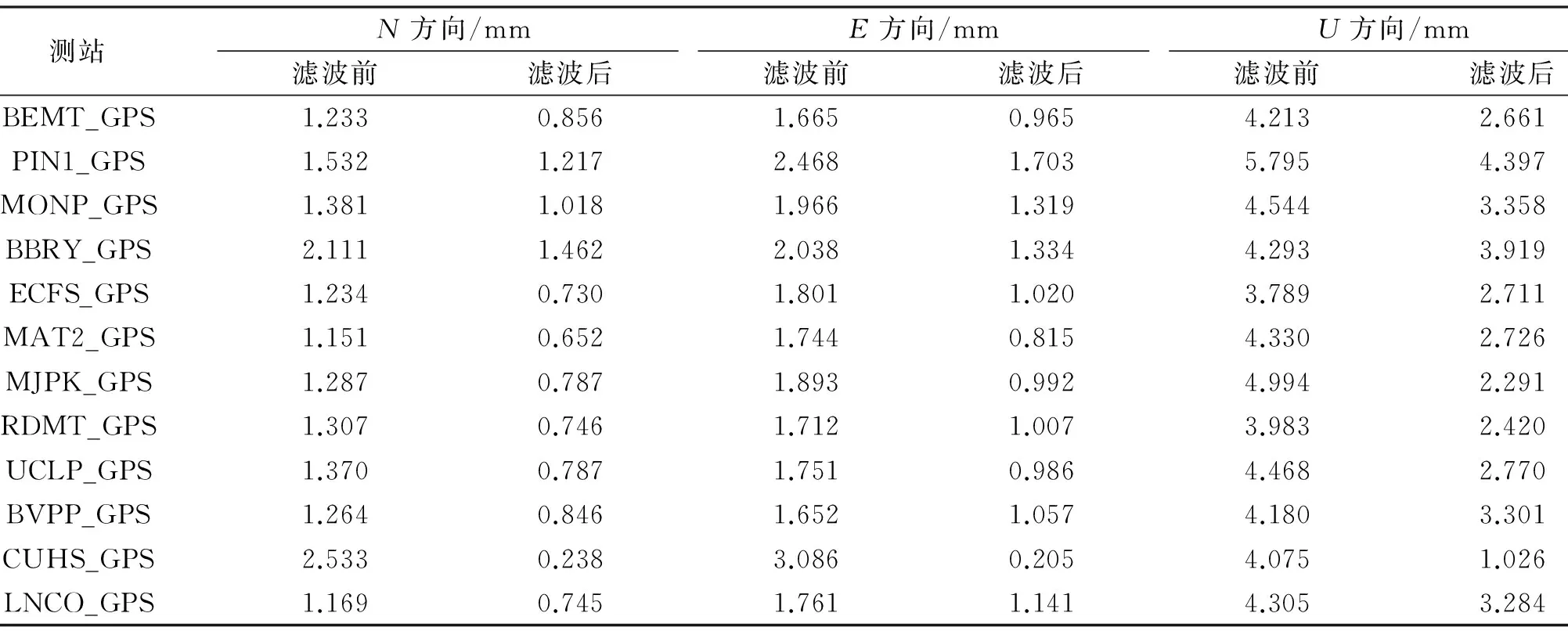
表2 400 km区域空间滤波前后残差坐标时间序列WRMS对比

对尺度大于600 km的空间进行区域滤波，通过表3、表4分析得出各站点在N、E、U3个方向上的加权均方根均有减少，但减少幅度明显小于420 km区域上的各点。这些站点中MNMC、MASW、HUNT、RNCH在E、N或U方向未滤波的时候WRMS有超过10，在这种情况下判定这些点本地效应严重。

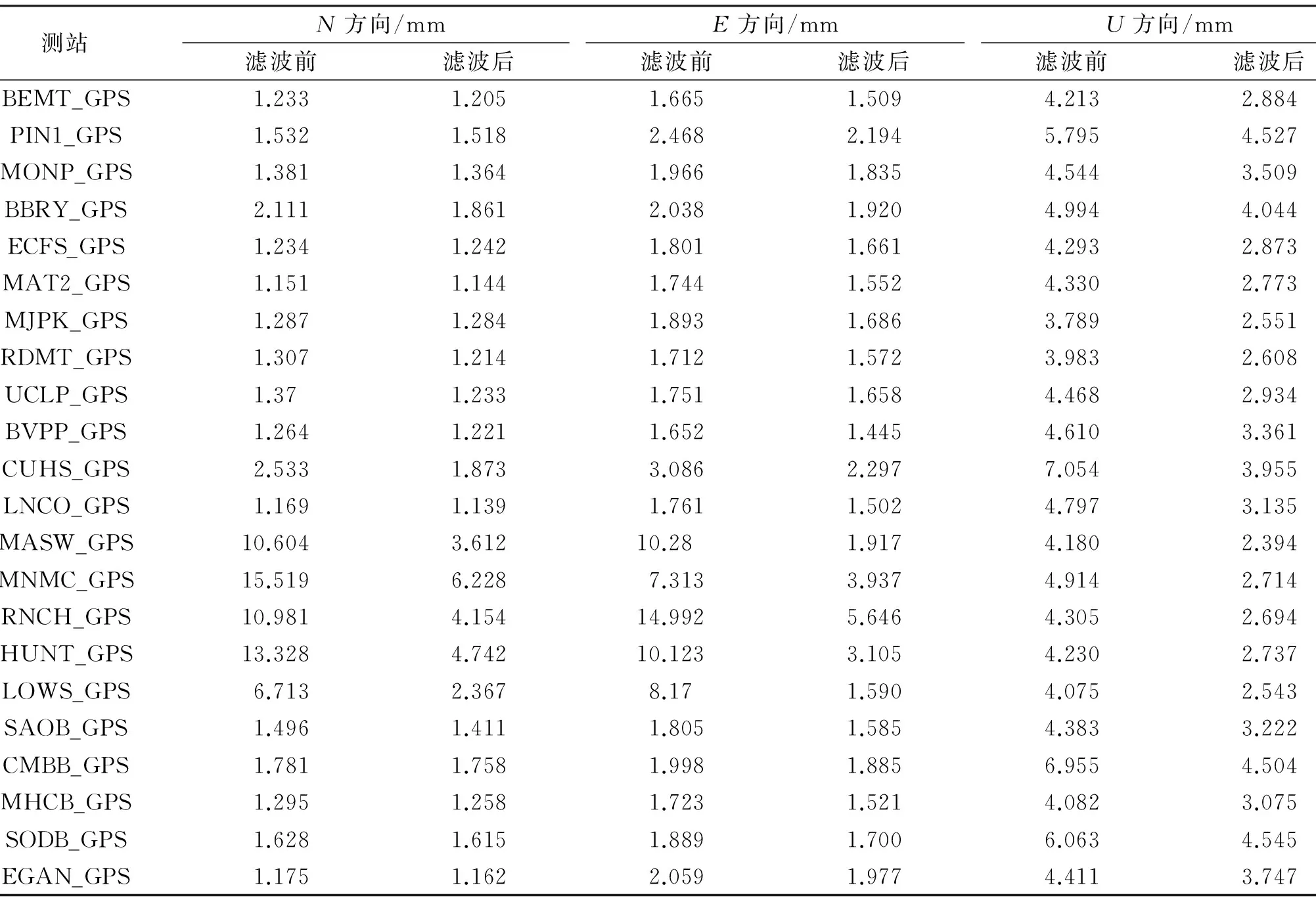
表3 600 km区域空间滤波前后残差坐标时间序列WRMS对比

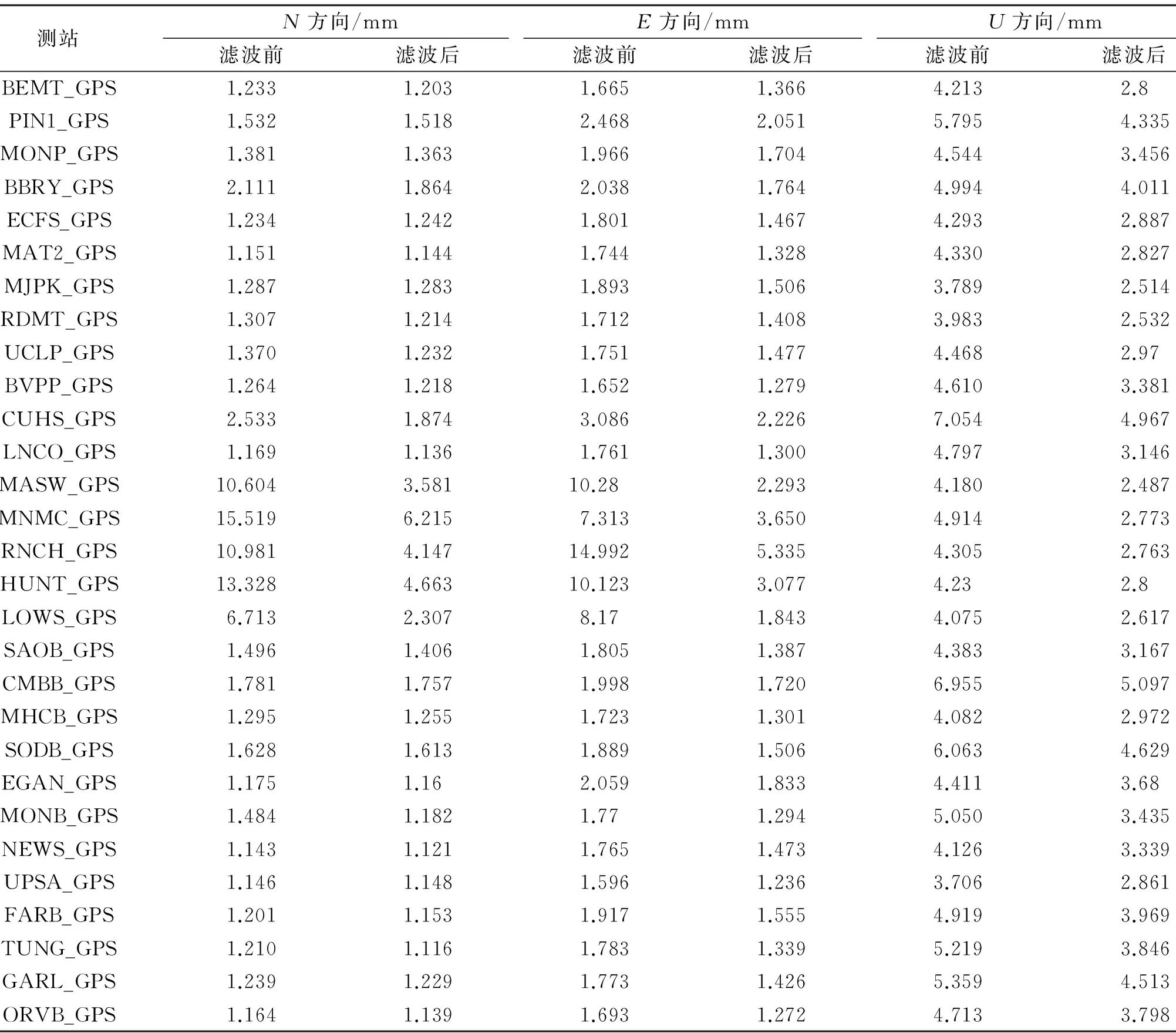
表4 1 000 km区域空间滤波前后残差坐标时间序列WRMS对比

根据地震记录及SOPAC发布的阶跃日志(ftp://sopac-ftp.ucsd.edu/pub/gamit/setup/siteOffsets.txt)可知，2003-12-22 San Simeon 6.5级地震和2004-09-28 Park Field 6.0级地震后，上述站点发生不同程度的阶跃，与上述WRMS异常判断相符合。在利用PCA提取共模误差时，由于阶跃的影响，使得主分量中包含本地效应，影响共模误差提取，因此在进行统计分析时应该剔除这些阶跃站点。图5(d)、5(e)、5(f)为滤波前后WRMS减少百分比曲线，结果表明，在E、N、U3个坐标分量上，WRMS平均减少约21.44%、6.88%、26.26%。根据两种尺度空间上所有站点WRMS的比较发现，各个方向平均WRMS减少的百分比，420 km尺度下均比1 000 km尺度下好很多，而且600 km、1 000 km空间区域滤波中WRMS的减少很多都在20%以下，420 km的时候大部分点的WRMS减少都在30%～40%，200 km的时候点的WRMS减少都在40%以上。结合图3可以得出，空间尺度大于600 km的时候，PCA区域叠加滤波方法效果不明显。

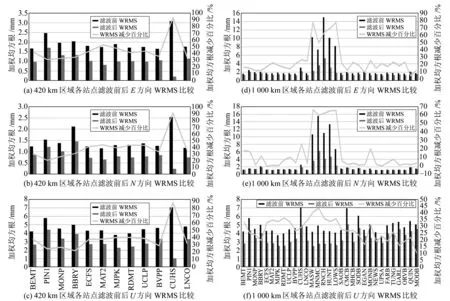
图5 400 km与1 000 km各站点滤波前后WRMS比较Fig.5 The site WRMS of 400km and 1 000 km before and after the filter

4 结 语

本文采用主成分分析的时空滤波方法，对不同空间尺度的GPS网进行共模误差分离，探讨共模误差的空间变化规律。结果表明，当GPS网在200 km尺度范围内时，PCA空间滤波效果最为明显；当GPS网的尺度增大到400 km～500 km时，在这个尺度区间中PCA滤波仍可以较好地提取出共模误差；当GPS网尺度大于600 km时，PCA空间滤波方法效果不是很理想，应该选取其他空间滤波方法(例如相关系数加权滤波)、分块区域滤波方法等。本文研究结果为大尺度GPS网共模误差的提取提供了一些参考，尤其是为区域尺度的划分提供了依据。

[1] 田云锋.GPS坐标时间序列中的异常高频周期性噪声[J].测绘科学, 2011, 36(1):26-28(Tian Yunfeng, Anomalous High Frequency Seasonal Noises in GPS Positions Time Series[J]. Science of Surveying and Mapping, 2011,36(1):26-28)

[2] Wdowinski S, Bock Y, Zhang J, et al. Southern California Permanent GPS Geodetic Array: Spatial Filtering of Daily Position for Estimating Coseismic and Post Seismic Displacements Induced by the 1992 Landers Earthquake[J]. Journal of Geophysical Research: Solid Earth(1978-2012), 1997, 102(B8):18 057-18 070

[3] 田云峰, 沈正康.GPS观测网络中共模分量的相关加权叠加滤波[J].地震学报.2011,33(2):198-208(Tian Yunfeng, Shen Zhengkang. Correlation Weighted Stacking Filtering of Common-Mode Component in GPS Observation Network[J].Acta Seismologica Sinica, 2011,33(2):198--208)

[4] 杨博, 占伟, 刘志广, 等. 多核函数法对GNSS 大空间域共模误差的识别[J].测绘科学技术学报.2014, 31(2):127-132(Yang Bo, Zhan Wei,Liu Zhiguang,et al.The Identification of GNSS Large Space Domain Common-Mode Error Based on Multi-Kernel Function Method[J]. Journal ofGeomatics Science and Technology. 2014, 31(2):127-132)

[5] 王敏, 张祖胜, 许明元,等.2000国家GPS大地控制网的数据处理和精度评估[J].地球物理学报, 2005,48(4):817-823(Wang Min, Zhang Zusheng, Xu Mingyuan, et al. Data Processing and Accuracy Analysis of National 2000 GPS Geodetic Control Network[J].Chinese J Geophys, 2005,48(4):817-823)

[6] Dong Danan. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research:Solid Earth,2006,111(B3)

[7] 黄立人.GPS台站坐标分量时间序列的噪声特性分析[J].大地测量与地球动力学, 2006,26(2):31-33(Huang Liren. Noise Properties in Time Series of Coordinate Component at GPS Fiducial Stations[J]. Journal of Geodesy and Geodynamics, 2006,26(2):31-33)

[8] 胡守超,伍吉仓,孙亚峰.区域GPS网三种时空滤波方法的比较[J].大地测量与地球动力学,2009,29(3):95-99(Hu shouchao, Wu Jicang, Sun Yafeng. Comparison Among Three Spatiotemporal Filtering Methods for Regional GPS Networks Analysis[J]. Journal of Geodesy and Geodynamics, 2009,29(3):95-99)

[9] Nikolaidis R. Observation of Geodetic and Seismic Deformation with the Global Positioning System[D], San Diego: University of California, 2002

[10]Jiang W P, Li Z, Dam T V, et al. Comparative Analysis of Different Environmental Loading Methods and Their Impacts on the GPS Height Time Series [J]. Journal of Geodesy,2013, 87(7): 687-703

Spatial Response Analysis for GPS Network CME

GONGGuodong1HEXiaoxing1,3HUAXianghong1,2SHUYing1DINGLinghang1

1 School of Geodesy and Geomatics, Wuhan University, 129 Luoyu Road,Wuhan 430079, China 2 Hazard Monitoring and Prevention Research Center, Wuhan University,129 Luoyu Road,Wuhan 430079, China 3 School of Civil Engineering and Architecture, East China Jiaotong University, 808 East-Shuanggang Street,Nanchang 330013, China

In GPS regional network coordinate time series, common mode errors (CME) are widespread. In order to extract CME, a sub-region is divided to get them superimposed and filtered. However, there is no principle to rely on for dividing sub-regions. According to the CME mentioned above, regarding three stations in southern California as centers, we divide the space into nine different spaces within different scales, carrying out the PCA space filtering method, to get the CME in each space scale. After analyzing and comparing the CME in each space scale, we can get the spatial response characteristics in CME, which provides a principle for the dividing sub-regions in the scale field.

GPS coordinate time series; CME; PCA; spatial filtering; spatial space

National Natural Science Foundation of China, No.41674005,41374011,41464001; Open Fund of Key Laboratory for Digital Land of Jiangxi Province, No.DLLJ201605.

HUA Xianghong, professor,PhD supervisor,majors in application and process of GNSS data, analyzing and processing the 3D laser scanning data, E-mail: xhhua@sgg.whu.edu.cn.

2015-10-28

项目来源：国家自然科学基金(41674005,41374011,41464001);江西省数字国土重点实验室开放研究基金(DLLJZ01605)。

龚国栋，硕士生，主要从事GNSS数据处理及精密工程测量研究，E-mail:1264392842@qq.com。

花向红，教授,博士生导师，主要从事GNSS数据处理及应用、三维激光扫描数据处理与质量评价研究，E-mail：xhhua@sgg.whu.edu.cn。

10.14075/j.jgg.2016.11.003

1671-5942(2016)011-0951-07

P228

A

About the first author:GONG Guodong, postgraduate,majors in high-rate GPS data processing and its application on engineering,E-mail:1264392842@qq.com.