对流层延迟模型映射函数研究

谢劭峰 张朋飞 王新桥 刘立龙

1 桂林理工大学测绘地理信息学院，桂林市雁山街319号，5410062 广西空间信息与测绘重点实验室，桂林市雁山街319号，541006 3 东海航海保障中心上海海事测绘中心，上海市共青路82弄7号，200086



对流层延迟模型映射函数研究

谢劭峰1,2张朋飞3王新桥1,2刘立龙1,2

1 桂林理工大学测绘地理信息学院，桂林市雁山街319号，5410062 广西空间信息与测绘重点实验室，桂林市雁山街319号，541006 3 东海航海保障中心上海海事测绘中心，上海市共青路82弄7号，200086

在介绍经验映射函数NMF和动态映射函数VMF1、GMF模型的基础上，利用ECMWF提供的格网数据，具体研究和分析了这3种映射函数1 a中的时间变化特征及其随高程、纬度、高度角变化的特点，并比较了3种映射函数随高度角的变化对斜路径延迟估计的影响。

GPS数据处理；对流层延迟；斜路径延迟；映射函数；时空变化

在高精度GPS数据处理中，对流层延迟是一个重要的影响因素。但是，直接求解电波经过对流层时各个方向的对流层延迟是比较困难的。基于球对称的假设，可以用天顶对流层延迟(ZTD)和映射函数(MF)的乘积来表示任意方向上的斜路径延迟。利用高精度的映射函数可以更准确地求出斜路径延迟，进而估算出大气中不同方向的水汽含量。因此，高精度映射函数的构建成为空间定位数据处理与GNSS实时遥感空间大气分布等领域的研究热点[1]。

1 常用的映射函数

根据不同的构造方式，映射函数可以分为3 大类：第一类是把大气折射积分中的被积函数按照高度角三角函数进行级数展开，然后对展开项进行逐项积分，最后求出大气折射的延迟，这种方法求得的映射函数称为经典映射函数，主要有Saastamoinen模型和Hopfield模型；第二类是上世纪70年代初期由Marini提出的连分式形式的映射函数，如Ifadis模型、MTT模型、NMF模型等，这类函数中的参数是通过对大量的经验资料拟合后获得；第三类是近年发展起来的动态映射函数，这种模型利用数值天气模型(numerical weather models, NWM)提供的高时空分辨率的对流层折射率数据，构建高精度的动态映射函数，如VMF、GMF。本文主要研究NMF、VMF1、GMF 3种映射函数的时空变化特征及其对斜路径延迟估计的影响。

1.1 尼尔映射函数(Niell mapping function,NMF)

Niell利用全球26个探空气球站资料，采用美国标准大气模式中北纬15°、30°、45°、60°、75°的一月份和七月份的湿度和温度廓线得出了NMF模型[2]。该模型考虑了南、北半球季节性的非对称性；映射函数包括干分量md和湿分量mw两部分，其中干分量中加入了与测站高程有关的改正项，能反映大气随高度角ε变化的规律。NMF模型的干分量md可表示为：

(1)

式中，H(ε)为与测站高程有关的改正项：

(2)

式中，aht=2.53×10-5,bht=5.49×10-3,cht=1.14×10-3,H为正高。

当测站纬度在15°～75°时，系数ad、bd、cd可以通过下式内插得到：

(3)

式中，p表示要内插的系数ad、bd、cd；t为年积日；t0=28为参考时刻的年积日；不同纬度的系数对应的平均值pavg和波动的幅度值pamp见表1。

测站纬度小于15°时，系数ad、bd、cd的计算公式为：

(4)

当测站纬度大于75°时，系数ad、bd、cd的计算公式为：

(5)

NMF模型的湿分量mw可表示为：

(6)

当测站纬度在15°～75°时，湿分量系数aw、bw、cw的求解和干分量系数相同。但是由于湿分量占整个对流层延迟的10%左右，比例较小，因此只考虑系数的平均值而不考虑波动项，插值公式可简化为：

(7)

式中，各个纬度系数的平均值见表2。

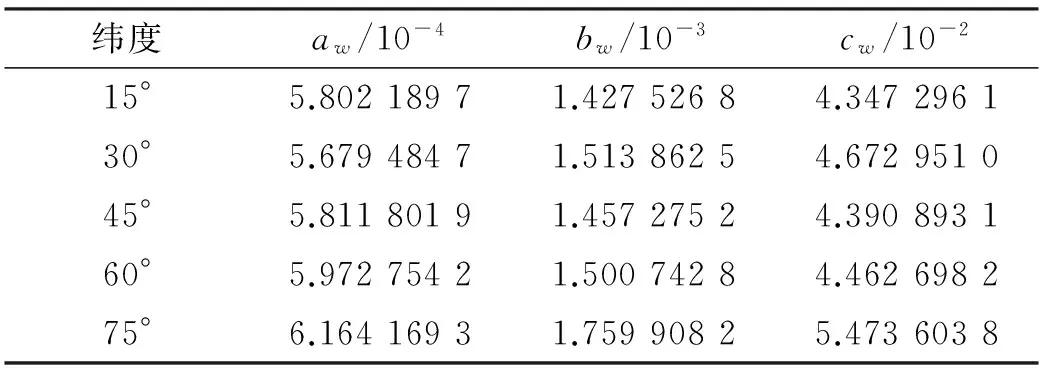
表2 NMF的湿分量内插系数

当测站的纬度小于15°或大于75°时，分别取15°和75°时的映射函数系数平均值pavg。

1.2 动态映射函数

1.2.1 维也纳映射函数(Vienna mapping function 1,VMF1)

维也纳理工大学的Boehm和Schuh采用NWM计算映射函数的方法得到了VMF模型[3]。VMF和NMF模型具有相同的数学表达式。为使ad和aw更好地符合欧洲中期天气预报中心(ECMWF)的NWM值，对VMF函数中系数b、c的数学表达式进行改进，得到的模型称为VMF1模型。它采用ECMWF 40 a的观测数据资料，重新估计对流层映射函数中系数b、c的值，而系数a的值则是利用实测数据事后时延34 h生成的2.5°×2°格网列表文件进行内插获得。VMF1模型的干分量系数ad和湿分量系数aw可以近实时地从网站下载(http://mars.hg.tuwien.ac.at/～ecmwf1/)，bd=0.002 9,bw=0.001 46,cw=0.043 91,cd通过下式拟合得到：

cd=c0+

(8)

式中参数c0、c10、c11和ψ可由索引表查取[3-4]。

1.2.2 全球映射函数(global mapping function,GMF)

为解决VMF1函数中系数ad和aw求解过程中的时间延迟问题，Boehm等提出了全球映射函数(GMF)模型[5]，其形式与NMF函数相似。GMF模型是在VMF1模型基础上，借鉴NMF建模思想，将年积日、经度、纬度、高程作为输入参数，将模型各个系数建立经验格网列表文件，按照与年积日有关的内插函数进行内插获得相应的模型系数值。GMF的系数通过将VMF1的参数扩展为一个全球的球谐面格网数据，其系数的确定只需要测站的位置和年积日。

利用ECMWF提供的40 a全球15°×15°分辨率的温度、压强和相对湿度的月平均廓线，采用高度角为3.3°的射线追踪法[5-7]，分析1999-09～2002-08的数据资料来确定系数ad和aw，而b、c仍采用VMF1 模型计算值。求解GMF模型系数ad和aw的表达式为：

(9)

平均值a0、振幅A的算法相同，都是通过将下面的球谐函数展开到9阶表达式计算得到：

(10)

2 NMF、VMF1、GMF模型的时空变化特征

2.1 3种映射函数的时间变化

为了分析这3种映射函数的时间变化，选择武汉站2012年全年的温度、压强、相对湿度等数据，分别采用NMF、VMF1和GMF进行处理。由于地理位置相同，除了选用的函数不同外，其他各项参数都相同，其中高度角设置为3°，得到的映射函数的周年分布见图1。

从图1可见，与NMF模型相比，GMF、VMF1模型的精度较高、符合较好，但VMF1模型的时间分辨率比GMF更高；湿映射函数较干映射函数离散，函数值波动较大，反映了对流层中水汽变化的不规律性；在夏秋季节映射函数值比冬春季节的明显要小。从图1还可以看出，NMF的湿映射函数的数值在全年保持为常数，说明该模型不能很好地反映湿延迟的年变化规律。

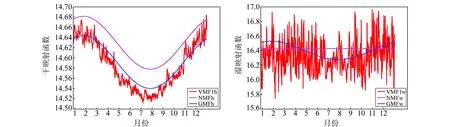
图1 3种映射函数的周年分布Fig.1 Annual distribution of three kinds of mapping functions

为研究这3种映射函数的逐月变化，通过仰角误差计算公式：

(11)

式中，θ0为视在仰角;r0为球心到卫星的距离;φ为地心张角;hT为目标真实海拔高度。据此可求得武汉全年的仰角误差改正值约为0.251°，取近似值0.25°作为仰角误差的改正值，从而可得真实仰角为3.25°。采用射线追踪法计算斜路径延迟和天顶延迟，通过三角函数反算计算映射函数值。以该值作为真值，与使用3种映射函数在仰角为3°时求得的结果进行比较，得到3种映射函数干分量和湿分量的月平均误差，见表3。

由表3可知，NMF模型的月平均误差在冬春季节较大、夏秋季节较小，而VMF1、GMF模型的月平均误差在夏秋季节较大、冬春季节较小；在冬春季节，NMF模型精度比VMF1、GMF模型明显要差，但在夏秋季节，NMF模型精度比VMF1、GMF模型要好。VMF1、GMF和NMF的干映射函数与射线追踪法取得的真值符合较好，而湿映射函数符合程度普遍较差，原因可能是因为干映射函数系数经过严格推导，而湿映射函数系数是忽略了波动项影响的近似表达。

表3 3种映射函数的月平均误差

图2是3种模型获得的干、湿映射函数误差的全年日变化。从图中可以看出，无论是干映射函数还是湿映射函数，VMF1和GMF都均匀分布于0值附近；夏秋季节，3种模型干分量多为负；冬春季节，GMF模型均为正；GMF、NMF的湿分量冬春季节均为正，夏秋季节多为负，VMF1模型湿分量冬春季节多为正，夏秋季节亦多为负，呈现比较明显的季节性特点；在120～270 doy时，NMF模型干湿分量全部为负值，说明NMF函数的日变化随机性较差，也就是说NMF模型比VMF1、GMF这2种模型的稳定性要差。

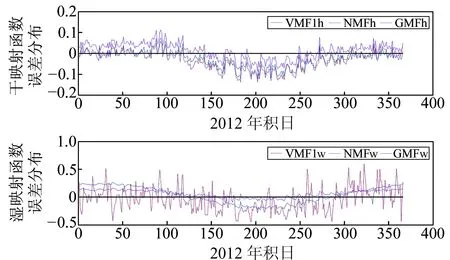
图2 3种映射函数误差的全年日变化Fig.2 Daily variation of three kinds of mapping functions in a year

2.2 3种映射函数的空间变化

这3种函数都有相同的输入参数：高程H、纬度lat和高度角ε。为确定这3种模型的空间变化特性，通过固定2个参数、改变第3个参数的方法进行数据处理。由于我国大部分地区处于中纬度，实验中选取纬度的变化起始点为北纬20°～50°。实验步骤如下：

1)固定高度角ε=3°和纬度lat=30.61°，使高程H从0 增高到10 km，变化步长为500 m；

2)固定高程H=23 m和纬度lat=30.61°，高度角ε分别取3°、4°、5°、6°、7°、8°、9°、10°、12°、15°、20°、30°；

3)固定高程H=23 m和高度角ε=3°，纬度变化步长为2°。

映射函数值随高程的变化见图3。从图3可以看出，3种函数的干映射函数值与高程呈线性关系，并随高程的增加而增大；而湿映射函数值与高程无关，为常数。GMF、VMF1两种模型的干映射函数值吻合得较好；VMF1、NMF两种模型的湿映射函数值相差较小。

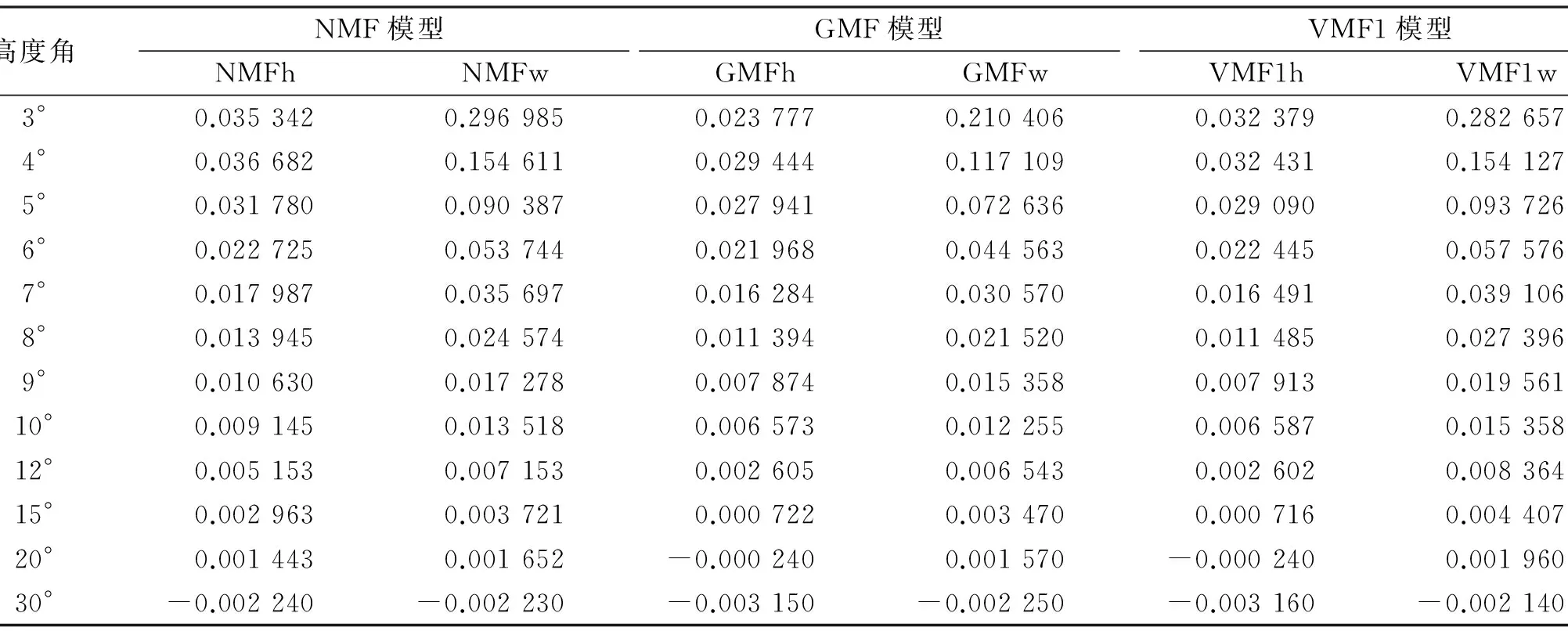
由表4可知，映射函数的误差随高度角的降低而增大；当高度角大于7°时，3种函数的精度相当；在高度角较小时，湿映射函数的误差较干映射函数大，动态映射函数GMF、VMF1模型较NMF模型精度高，其中GMF的精度更高、稳定性更好，因此在处理低高度角数据时，宜选用动态映射函数。

从图4可以看出，随着纬度的变化，GMF和NMF的干、湿映射函数值大体呈线性变化，而VMF1的干、湿映射函数值分布的随机性比较大；3种模型的干映射函数值都随纬度的增加而增大；GMF和VMF1模型的湿映射函数值亦随纬度的增加而增大，但NMF的湿映射函数值随纬度增加而有所减小。

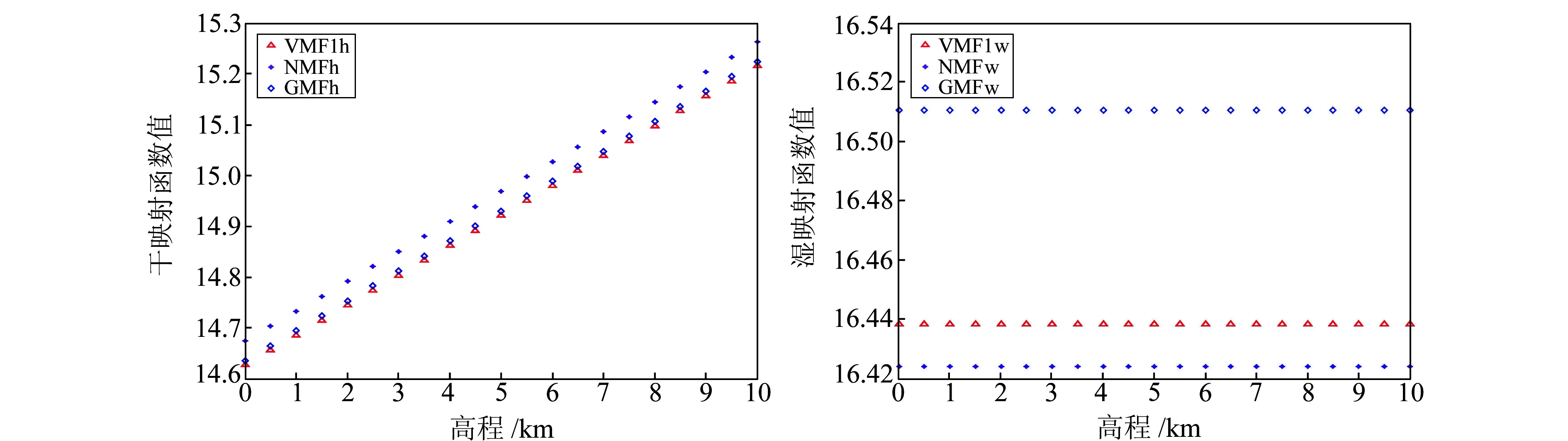
图3 3种映射函数值随高程的变化Fig.3 Variation with height of three kinds of mapping functions’ value

高度角NMF模型GMF模型VMF1模型NMFhNMFwGMFhGMFwVMF1hVMF1w3°0.0353420.2969850.0237770.2104060.0323790.2826574°0.0366820.1546110.0294440.1171090.0324310.1541275°0.0317800.0903870.0279410.0726360.0290900.0937266°0.0227250.0537440.0219680.0445630.0224450.0575767°0.0179870.0356970.0162840.0305700.0164910.0391068°0.0139450.0245740.0113940.0215200.0114850.0273969°0.0106300.0172780.0078740.0153580.0079130.01956110°0.0091450.0135180.0065730.0122550.0065870.01535812°0.0051530.0071530.0026050.0065430.0026020.00836415°0.0029630.0037210.0007220.0034700.0007160.00440720°0.0014430.001652-0.0002400.001570-0.0002400.00196030°-0.002240-0.002230-0.003150-0.002250-0.003160-0.002140

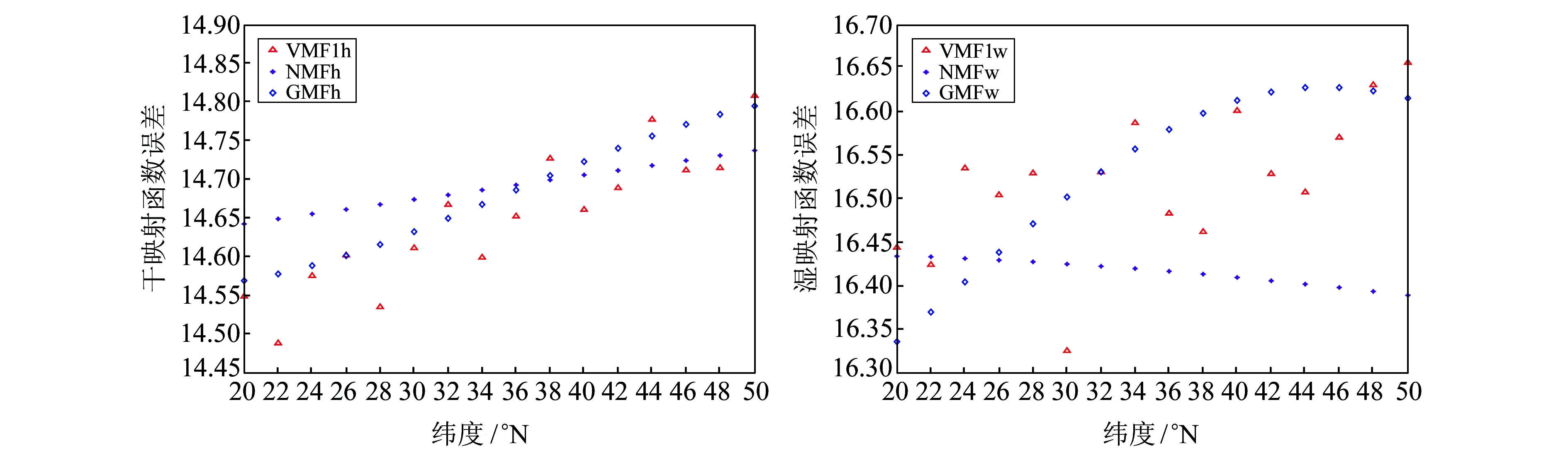
图4 3种映射函数误差随纬度的变化Fig.4 Variation with latitude of three kinds of mapping functions’ error

3 3种映射函数对斜路径延迟估计的影响

选用2012年积日150 d的URUM站数据，不考虑电波的方位角，仅仅设置高度角为变量，分别计算3种映射函数的斜路径延迟，结果见表5。由表5可知，在高度角为1.87°时，3种模型计算的斜路径延迟差别明显，其中GMF与VMF1相差95.4 mm，GMF与NMF相差80.2 mm，NMF与VMF1相差15.2 mm；当高度角为7.07°时，GMF与VMF1相差5.6 mm，GMF和NMF相差4.3 mm，VMF1和NMF相差1.3 mm；当高度角大于等于15°时，3种映射函数求得的斜路径延迟之差均小于1 mm。可见，当高度角较大时，3种映射函数计算的斜路径延迟相当，无明显差别；但是随着高度角的降低，求得的斜路径延迟的差值逐渐增大。因此在计算低高度角数据的斜路径延迟时，应注意选择合适的映射函数。

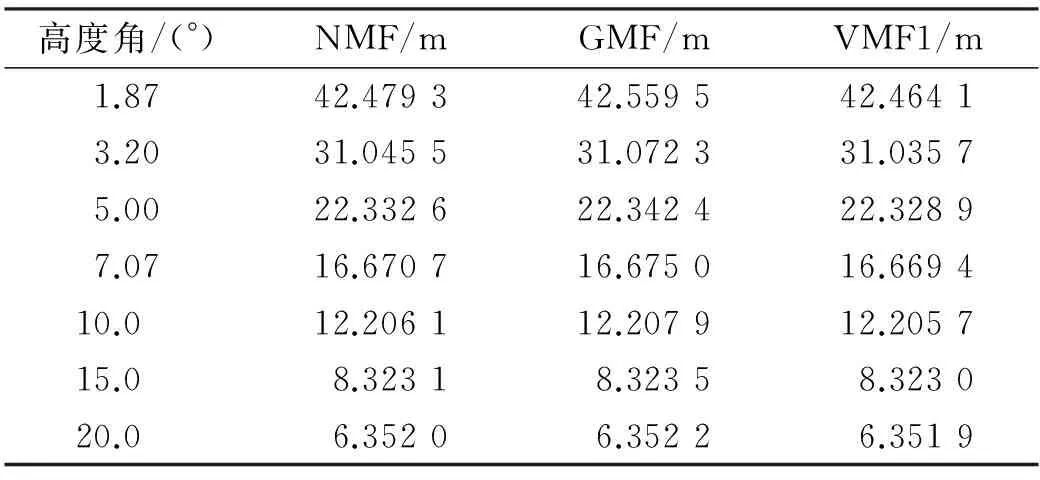
表5 URUM站3种映射函数解算的斜路径延迟

4 结 语

映射函数误差在时间变化方面，3种函数均呈现比较明显的季节变化，冬春季节与夏秋季节差异比较明显。在空间变化方面，随着纬度和高程的增加，映射函数误差相应增大；映射函数误差随高度角的降低而增大；高度角较大时，3种函数的精度相当，但在低高度角时，GMF、VMF1模型均较NMF模型精度高。3种模型计算低高度角数据的斜路径延迟时差别明显，此时应注意映射函数的选择。

[1] 张双成，叶世榕，刘经南 等.动态映射函数最新进展及其在GNSS遥感水汽中的应用研究[J].武汉大学学报：信息科学版，2009,34(3):280-283(Zhang Shuangcheng, Ye Shirong, Liu Jingnan, et al. Latest Progress of Dynamic Mapping Functions and Its Application to GNSS Retrieved Water-Vapor[J].Geomatics and Information Science of Wuhan University, 2009,34(3):280-283)

[2] Niell A. Global Mapping Functions for the Atmosphere Delay at Radio Wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996,101(B2):3 227-3 246

[3] Boehm J, Schuh H. Vienna Mapping Functions in VLBI Analysis[J].Geophysical Research Letters, 2004, 31(1)

[4] Boehm J, Cerveira P, Schuh H, et al. The Impact of Tropospheric Mapping Functions Based on Numerical Weather Models on the Determination of Geodetic Parameters[C]. IAG Proceedings, Cairns, 2005

[5] Boehm J, Niell A, Tregoning P, et al. Global Mapping Function(GMF):A New Empirical Mapping Function Based on Numerical Weather Model Data[J].Geophysical Research Letters, 2006,33(7):199-208

[6] 张瑜，袁秋林. 雷达至目标的电波射线描迹方法研究[J]. 河南师范大学学报:自然科学版, 2006,34(2): 50-53(Zhang Yu, Yuan Qiulin. The Method Research of Radiowave Radial Track Description from Radar to Objective[J].Journal of Henan Normal University: Natural Science, 2006,34(2): 50-53)

[7] 郭际明，章迪，史俊波，等.利用射线追踪法分析三种典型对流层映射函数在中国区域的精度[J].武汉大学学报:信息科学版，2015,40(2): 182-187(Guo Jiming, Zhang Di, Shi Junbo,et al. Using Ray-Tracing to Analyse the Precision of Three Classical Tropospheric Mapping Functions in China[J].Geomatics and Information Science of Wuhan University, 2015,40(2): 182-187)Research on the Mapping Functions for Tropospheric Delay Model

XIEShaofeng1,2ZHANGPengfei3WANGXinqiao1,2LIULilong1,2

1 College of Geomatics and Geoinformation, Guilin University of Technology, 319 Yanshan Street, Guilin 541006, China 2 Guangxi Key Laboratory of Spatial Information and Geomatics, 319 Yanshan Street, Guilin 541006, China 3 Hydrography Department Shanghai Maritime Safety Administration, Donghai Navigation Safety Administration,7 Lane 82, Gongqing Road,Shanghai 200086, China

On the basis of introducing the empirical mapping function NMF and the dynamic mapping functions VMF1 and GMF, using one year’s grid data provided by ECMWF, the time varying characteristics of these three mapping functions and their variations with height, latitude and elevation angle are concretely researched and analyzed are compared. Finally,we compare the influence on slant path delay with the variations of elevation angle in the three kinds of mapping functions are compared.

GPS data processing; tropospheric delay; slant path delay; mapping function; temporal and spatial variation

National Natural Science Foundation of China, No.41064001, 41541032; Guangxi Key Laboratory of Spatial Information and Geomatics Foundation, No.15-140-07-11, 14-045-24-10.

ZHANG Pengfei,assistant engineer, majors in GPS data processing and application, E-mail: 879333424@qq.com.

2015-12-13

项目来源：国家自然科学基金(41064001, 41541032)；广西空间信息与测绘重点实验室基金(15-140-07-11, 14-045-24-10)。

谢劭峰，副教授，主要研究方向为GPS数据处理与应用，E-mail: xieshaofeng111@126.com。

张朋飞，助理工程师，主要研究方向为GPS数据处理与应用，E-mail: 879333424@qq.com。

10.14075/j.jgg.2016.11.001

1671-5942(2016)011-0941-05

P228

A

About the first author:XIE Shaofeng, associate professor, majors in GPS data processing and application,E-mail: xieshaofeng111@126.com.