基于分簇门限反馈的机会波束成形算法研究

陈兴旺，许小东

(中国科学院无线光电通信重点实验室，中国科学技术大学信息科学技术学院，安徽合肥 230027)



基于分簇门限反馈的机会波束成形算法研究

陈兴旺，许小东

(中国科学院无线光电通信重点实验室，中国科学技术大学信息科学技术学院，安徽合肥 230027)

在波束间存在干扰的小区通信场景中，研究满足反馈用户数约束条件时，如何有效运用机会波束成形(ORBF)算法实现和速率最大化的问题.针对该问题，提出了一种基于分簇门限反馈的ORBF算法.首先，将问题建模为基于反馈用户数约束的和速率最大化优化问题.然后，根据用户信噪比信息对小区内各用户进行分簇处理，并在各簇内利用极值理论工具独立设置反馈门限.最终，在分簇基础上构造出多门限反馈的ORBF算法.对算法性能进行理论分析，获得了和速率损失量上界的闭合表达式以及多用户分集增益的渐进形式.仿真实验验证了理论分析的正确性，同时表明，该算法与经典ORBF算法相比，能够在极大降低反馈量的同时取得很好的和速率性能.

机会波束成形；波束间干扰；分簇；反馈门限

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.025

1 引言

多输入多输出(Multiple Input Multiple Output,MIMO)技术能够在不增加功率和带宽的情况下成倍增加传输速率和大幅度改善链路可靠性，被公认为能有效缓解频谱资源紧张并提供高速率业务支持的一项关键技术.大量的研究已经证明，多用户分集增益可以大幅度地提高MIMO系统的容量，多用户分集技术也已经运用到一些移动通信系统中[1,2].对于MIMO广播信道，脏纸编码(Dirty Paper Coding,DPC)可以取得广播信道的容量界[3]：Mlog log(NK)，其中M为发射天线数，N为用户的接收天线数，K为总的用户数，但是DPC的编/解码过程都非常复杂，影响其实用性.因此，一种次优的迫零波束成形方法[4]被提出来并被用于优化广播系统容量.由于上述方法均要求发射端获取所有用户的完整信道状态信息(Channel State Information,CSI)，因此系统所需的反馈开销较高，且随着用户数的增加，所需反馈量线性增长，从而导致此类方法难以在实际系统中有效应用.

为了降低反馈开销，许多波束成形方法通过对反馈信息及其数量进行有效控制，研究如何减小有限反馈引起的容量损失.一种方法是对用户反馈信息进行量化[5,6]，从而来有效降低反馈量.另一种低反馈开销的波束成形技术是机会波束成形(Orthogonal Random Beamforming,ORBF)，本文以下将其称为经典ORBF技术[7].在经典ORBF技术中，用户不再反馈完整的CSI信息，而是只需要反馈信干噪比(Signal to Interference plus Noise Ratio,SINR)和最优的波束序号.研究表明，当用户趋于无穷时，ORBF技术可取得与DPC具有相同渐进形式的系统容量.值得注意的是，在经典ORBF技术中仍需要所有用户参与反馈.为进一步降低反馈量，假设小区内各用户具有相同的接收信号强度(或者说各用户接收信噪比相同)，文献[8]提出一种基于门限阈值的反馈机制，即当且仅当用户的SINR高于门限阈值时，该用户才参与反馈，否则该用户不反馈任何信息.另一种门限反馈策略通过优化门限阈值，可将反馈用户数从K降低到了log(K)，Diaz等人还对该策略引入的容量损失进行了细致分析[9].更进一步，文献[10]设计一种门限策略，可保证参与反馈的用户数始终处于相同量级.文献[11]讨论了当小区内用户具有不同接收信号强度时，基于用户平均信噪比进行用户分簇，然后在簇内设置门限并选择簇间最小门限作为反馈阈值的单门限反馈策略.然而，该策略仅局限于发送端和接收端配置相同天线数的特殊情况，并未考虑收、发端配置不同天线数时，波束间存在干扰的现实问题.

考虑存在波束间干扰的小区场景，本文在文献[11]基础上假设所有接收用户仅配置1根接收天线，研究满足反馈用户数约束条件时，如何有效运用ORBF算法实现和速率最大化的问题.与文献[11]不同之处在于：(1)本文考虑用户仅配置1根接收天线，故接收端无法完全消除其他波束对该用户形成的干扰，因此在分析获得用户SINR的基础上提出了相应的分簇新方法；(2)本文提出了一种新的反馈门限设置策略，并基于该策略设计实现一种采用多反馈门限的ORBF算法，从而能够在满足反馈用户数约束条件下取得最优和速率.

2 系统模型与问题描述

考虑多用户MIMO系统下行链路，基站配置M根发射天线，K个均配置单根天线的用户.根据经典ORBF算法，基站产生M个正交波束向量φm∈M×1,(m=1,…,M) 并使用这些向量发送M个数据流.sm(t)表示在t时刻第m个发送符号，则时刻t发送符号向量表示为：

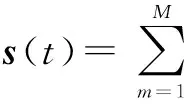
(1)

yk(t)表示用户k的接收信号，即：

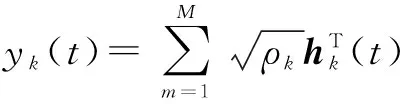
(2)

其中，hk∈M×1是用户k的信道向量，hk的各元素是服从CN (0,1)独立同分布(i.i.d)的复数，这种假设意味着该信道符合小尺度瑞利衰落.vk(t)为服从CN (0,1)的加性高斯白噪声.ρk表示由路径损耗和阴影衰落等造成的大尺度信道衰落因子，小区内用户位置分布的差异性导致了不同用户所对应的ρk也不相同.发射功率设定为1，即：E[sHs]=1，因此ρk同时表示了用户k的接收信噪比.为了书写方便，时间变量t在下文中将被省略.根据式(2)，用户k对于第m个波束的SINR为：

(3)

根据文献[12]，SINRk,m对应的概率密度函数fSINRk,m和累积分布函数FSINRk,m可分别表示为：

(4)

(5)

经典ORBF算法的基本思想是：每个用户反馈最大SINR及其对应的波束序号，基站则为每个波束选择具有最大SINR的用户进行通信.因此，经典ORBF算法可取得的平均和速率(bps/Hz)可以写成:

(6)

相比于经典ORBF算法，本文所关注的问题在于：在给定反馈用户数目约束条件下，如何设计基于门限反馈策略的ORBF算法，以最大化系统和速率.此问题模型可表述如下:

maxRsum(τ), s.t. F (τ)=λ

(7)

其中，τ是门限向量，F (τ)表示在ORBF算法中采用门限反馈策略后的反馈用户数，Rsum(τ)是采用门限反馈策略后取得的和速率，λ是期望反馈用户数.

3 基于门限反馈的ORBF算法

鉴于各用户接收信噪比之间的差异性，直接求解问题(7)十分复杂.因此，本文借鉴文献[11]的处理思想，提出一种基于分簇门限反馈的ORBF算法.该方法对小区内所有用户首先进行分簇，进而将同一簇内的用户近似看成是具有相同的接收信噪比.根据式(4)和式(5)可以看出，此时簇内用户的SINR分布将变得相同，从而降低问题的求解复杂度.在分簇的基础上，该方法设计簇内反馈门限，并在簇间采用不同门限控制反馈用户数.接下来，我们将具体阐述本文提出的算法.

3.1 分簇方法

由于不考虑波束间干扰，文献[11]提出了一种直接根据用户SNR的统计信息进行分簇的方法：首先，基站需要得到各用户所反馈SNR的统计均值信息，然后根据用户SNR均值对用户进行排序.注意到，在基站和用户端配置相同天线数时，关于SNR均值的计算较为容易.然而，对于用户端配置单天线、基站多天线的情况，由于波束间干扰的存在，按照文献[11]的分簇方法，必须计算用户的SINR均值.由于SINR分布的复杂性，这项工作不易实现.因此，本文提出一种基于用户接收信噪比ρk对用户进行分簇的方法.从式(4)和式(5)容易看出，用户的SINR分布主要取决于ρk的信息，因此用户的ρk能够在很大程度上表征用户SINR，说明根据ρk对用户进行分簇是合理可行的.

具体的分簇方法描述如下：

(1)基站根据用户之前反馈的SINR信息得到用户的平均接收信噪比ρk[12]，按照ρk递增的顺序对用户进行排序，即：{ρ(1)≤ρ(2),…,≤ρ(k)}.

(2)将排序后的ρk均匀地分成N个簇，这里为了便于讨论，假设总用户数K和簇数N满足关系：L=K/N，则L表示各簇内平均用户数.最终得到各簇内用户ρk的集合：{ρ(1),ρ(2),…,ρ(L)},…,{ρ((N-1)L+1),ρ((N-1)L+2),…,ρ(NL)}.

3.2 门限设置方法

从和速率的表示式(6)中容易发现：SINR对系统和速率性能起到了关键作用.由于存在对SINR取最大值运算，因此极值理论(Extreme Value Theory,EVT)可以被运用到问题的求解中.为了便于分析说明，下面简要地介绍极值理论中的一些基本概念和结论.

3.2.1 EVT

一组独立同分布的变量x1,x2,…,xL，其累积分布函数为F，令AL=max(x1,…,xL)表示变量中的最大值，则AL的分布为：

Pr(AL≤z)=Pr(X1≤z,…,XL≤z)

=Pr(X1≤z)…Pr(XL≤z)=FL(z)

(8)

当L→∞时，如果存在常数序列aL>0和bL∈，使得Pr{(AL-bL)/aL}→G(z)，则G(z)收敛于下列三种分布中的一种：Weibull，Gumbel和Frechet.其中，G(z)服从Gumbel分布的充分条件为：

(9)

各簇内用户SINR的概率密度函数f(x)和累计分布函数F(x)分别如式(4)和式(5)所示，式(9)很容易得到验证.因此，若将请求第m个波束的所有用户中的最大SINR记为SINR*(m)=max1≤k≤nmSINRk,m，则存在序列aL>0和bL∈使得(SINR*(m)-bL)/aL收敛于Gumbel分布，即：当L→∞，对于任意x∈，FL(aLx+bL)→exp(-e-x).aL和bL可以通过如下数学关系式计算得到[13]：

1-F(bL)=1/L

(10)

和

(11)

因此，通过求解式(10)和式(11)，可以得到不同簇内的ai,L,bi,L,(i=1,…,N)，其具体表达式为：

(12)

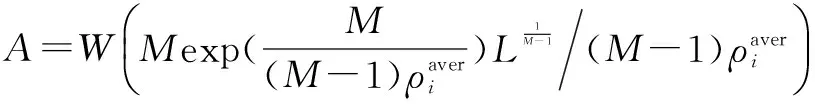
而W(*)是Lambert函数，其定义为W(x)exp(W(x))=x，x≥-1/e.

3.2.2 簇内门限设置

文献[14]已经讨论了当用户具有相同SNR时，在给定反馈用户数约束条件下，通过设置门限来取得最大化和速率的问题，作者得出了如下理论结果：如果用户信道为瑞利衰落信道，当基站发送波束数M≥2时，为所有用户设置同一门限值，便可以在满足反馈约束时取得最大系统和速率.由于当M=1时，无法获得空间复用增益，一般情况下，系统采用多个波束取得的和速率要优于单波束的情况，因此本文只考虑M≥2的情况.

在经过分簇后，由于各簇内用户可以看成是具有相同的SNR，基于文献[14]的已有结论，我们可以通过在各簇内设置单一门限来取得最大系统和速率.值得注意的是，在经典ORBF算法中，必须要保证用户之间的调度公平性，即,尽量保证各用户被基站调度的概率相同.因此当给定反馈用户数约束值λ，需要确保分配到各簇内的反馈用户数是相等的，即,λi=λ/N,(i=1,…,N)，从而来保证用户间的调度公平性.

基于上述分析，分别在各簇内设置满足约束条件λi的门限，便可以求解问题(7).参考文献[10]，本文设计了一种满足反馈用户数约束条件的单个门限设置方法，并得出一些新的结论.由于采用分簇后，各簇内的用户可以看成信噪比相同，因此在各簇内将门限设置为[10]：

τi=ai,Lx+bi,L,(i=1,…,N)

(13)

其中ai,L和bi,L如式(12)所示，x是一个被设计用来满足反馈约束条件的自由变量.

与文献[9]不同的是：由于在各簇内分别设置反馈门限，因此需要设置N个门限，而不再仅仅是单个门限.考虑到存在N个门限并且各簇之间的用户参与反馈的过程是相互独立的，采用类似于文献[10]中的证明方法(这里省略证明过程)，可以得到如下性质：

性质1 当用户数趋于无穷时，系统总的反馈用户数为MNe-x，即,每个波束的平均反馈用户数为Ne-x.因此可以通过选择符合MNe-x=λ的x来满足反馈约束条件.

性质2 当用户数趋于无穷时，系统的中断概率为exp(-Ne-x).

从上面两个性质容易发现：在用户数趋于无穷时，如果给定反馈用户数约束值λ和发送波束数M，那么Ne-x=λ/M便是一个常量.因此，分簇个数N对系统的中断概率和反馈用户数均无影响.然而，当用户数是有限值时，分簇个数的多少会影响系统的性能，对系统性能的具体影响将在后文进行详细讨论.

3.3 算法步骤

综上所述，在采用分簇和门限反馈策略的基础上，本文提出了一种基于分簇门限反馈的ORBF算法，算法的具体步骤描述如下：

(1)对用户进行分簇.基站利用用户所反馈的SINR信息，根据所提出的分簇方法对用户进行分簇.

(2)在各簇内计算得到门限集合{τ1≤τ2≤,…,≤τN}.基站根据ρk，L以及λ等参数按照介绍的门限设置方法计算得到各簇内门限.

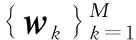
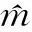
4 性能分析

4.1 和速率损失量

与经典ORBF算法相比，本文所提出的算法存在和速率损失量的主要原因是：由于反馈门限的设置，对于某些波束，可能发生无用户请求的情况，从而发生中断事件，导致和速率损失.一般而言，随着分簇数的增加，一方面，簇内用户的SNR差异性降低，用SNR的均值来表征所有用户SNR也更加合理；另一方面，降低了具有低SNR用户的反馈门限值，使得这部分用户具有更高的概率参与反馈，这两方面原因使得和速率损失量减少.在本小节中，我们将要分析采用分簇门限反馈所导致的和速率损失.

当中断事件发生时，基站无法为波束选择一个合适的用户进行通信，因而导致和速率损失.其中，中断概率PL(K)在性质2中已经给出：PL(K)=exp(-Ne-x)=exp(-λ/M).

ΔR(K,N,M,λ)=ME{log2(1+Z(1))}PL(K)

(14)

对于ΔR(K,N,M,λ)的计算，关键是如何求得E{log2(1+Z(1))}.本文借助于极值理论及顺序统计(order statistics)中的部分结论来求解，求解过程中主要用到下面两个定理.

定理1[15]一组随机变量Z1,Z2,…,ZL，令Z(1)=max(Z1,Z2,…,ZL)表示变量中的最大值，如果(Z(1)-μ)/σ收敛于标准的Gumbel分布，则随机变量的均值和方差分别为μ和σ，可以通过如下关系式求得:

(15)

(16)

(17)

根据定理1，可以求得各簇内用户SINR的均值和方差，即μi和σi(i=1,…,N).然后，根据定理2中E{Z(1)}的上界表达式(17)以及杰森不等式.最终，求得和速率损失量上界的表达式，可以写成:

ΔR(K,N,M,λ)=ME{log2(1+Z(1))}PL(K)

≤M{log2(1+E{Z(1)})}PL(K)

(18)

根据和速率损失量表达式(18)，本文还可以得出如下新结论.

定理3 给定M、N及λ，和速率损失量ΔR(K,N,M,λ)随着用户数K的增加而增加.

W(x)≈alog2(x+b)+c

(19)

其中a=0.4264，b=0.6683，c=0.2547.

(20)

其中C=log2(AL1/(M-1)+b).

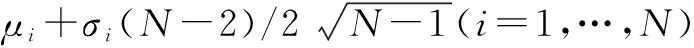
因此当取

4.2 多用户分集增益

本节将要分析基于分簇门限反馈的ORBF算法所取得的多用户分集增益性能.多用户分集增益可以表示为当用户数趋于无穷时，算法取得的和速率与用户数之间的渐进关系.基于分簇门限反馈的ORBF算法取得的和速率R(K,N,M,λ)可以写成:

R(K,N,M,λ)=R(K)-ΔR(K,N,M,λ)

(21)

其中，R(K)为经典ORBF算法取得的和速率，ΔR(K,N,M,λ)为所提出算法的和速率损失量.

针对于式(21)，当用户数趋于无穷时，和速率具有如下性质.

定理4 给定N、M和λ，基于分簇门限反馈的ORBF算法取得的和速率R(K,N,M,λ)满足:

(22)

(23)

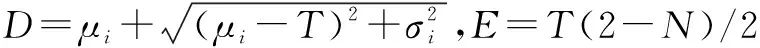
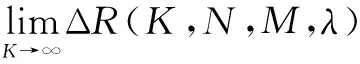
(24)

将式(24)代入可知：

(25)

证毕.

根据定理4，当给定N，M及λ，当用户数趋于无穷时，基于分簇门限反馈的ORBF算法所取得和速率的渐进形式为(1-e-λ/M)Mlog2log2K.这意味着，采用分簇门限反馈的ORBF算法能取得最优和速率的部分性能1-e-λ/M.实际上，e-λ/M正是当用户数趋于无穷时系统的中断概率PL(K)，这与本文前面部分提到的关于和速率损失主要是由中断事件造成的结论相一致.

5 仿真实验

本节将通过蒙特卡罗仿真实验来检验所提出的基于分簇门限反馈的ORBF算法性能.仿真时假设基站配置4根发射天线，用户端配置单根天线，信道为瑞利衰落信道，用户的SNR均匀分布在[0,10]dB，发射波束数等于发送天线数，即M=4.

5.1 检验分簇门限反馈策略

分簇门限反馈策略的正确性验证主要是通过验证所采用的门限设置方法是否满足约束条件来实现，具体可以分为两种情况分别检验.情况1：λ取值仅受分簇数影响；情况2：λ取值恒定不变.

情况1 由于理论分析已给出关系式λ=NMe-x，因此为了达到取不同λ的目的，一种方法是保持分簇数N不变、改变x；另一种方法是改变N、保持x不变.显然单纯的改变x而保持N不变较为简单并且无法反应出不同分簇个数对算法的影响.因此在仿真中，我们选择采用不同分簇数N来改变λ.令x=0，则λ=NMe-x=4Ne0=4N.很明显，此时λ会随着N的变化而改变.图1给出了在不同约束条件下，反馈用户数与总用户数的关系曲线.根据性质1，每个波束的平均反馈用户数的理论分析值为Ne-x=Ne0=N.从该曲线中容易看出仿真值与理论分析结果一致，从而验证了当约束条件λ取不同值时，门限反馈策略能够满足指定约束条件.

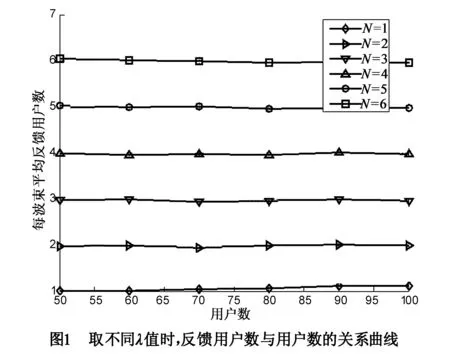
情况2 由于λ给定，此时的x不再保持不变而是随着N的改变而变化，满足MNe-x=λ.仿真中取λ=16，则每个波束的平均反馈用户数理论值为Ne-x=4，仿真结果如图2所示.从图中可以看出，随着用户数的增加，仿真结果逐渐趋近于理论分析值.综合图1和图2的仿真结果，可以得出结论：所采用的分簇门限反馈的方法，可以很好的满足反馈用户数约束条件.

5.2 检验和速率损失量

为了验证新算法的和速率损失量，也可以依前一小节分为两种情况分别讨论，即，情况3和情况4，仿真结果分别如图3和图4所示.

情况3 在本次仿真仿真中，依然取x=0，则对应的λ=MNe-x=4N，仿真结果如图3所示.从图中曲线可以得到以下三点结论：首先，对于不同的分簇数目，随着用户数的增加，和速率损失值的仿真结果与理论分析上界逐渐逼近；即使在用户数较少时，仿真值仍然与分析值比较接近，从而验证了关于和速率损失量理论分析值的正确性.其次，和速率损失量随着用户数K的增加而增加，验证了定理3的正确性.最后，可以看出和速率损失量随着反馈用户数的增加而减少，即， 随着N的增大而减少.究其原因，可能是由于增大反馈用户数λ，意味着更多的用户参与反馈，这样则降低了系统中断概率，从而使得和速率损失量降低.

情况4 本次实验中令λ=16，即每个波束反馈4个用户，仿真结果如图4所示.

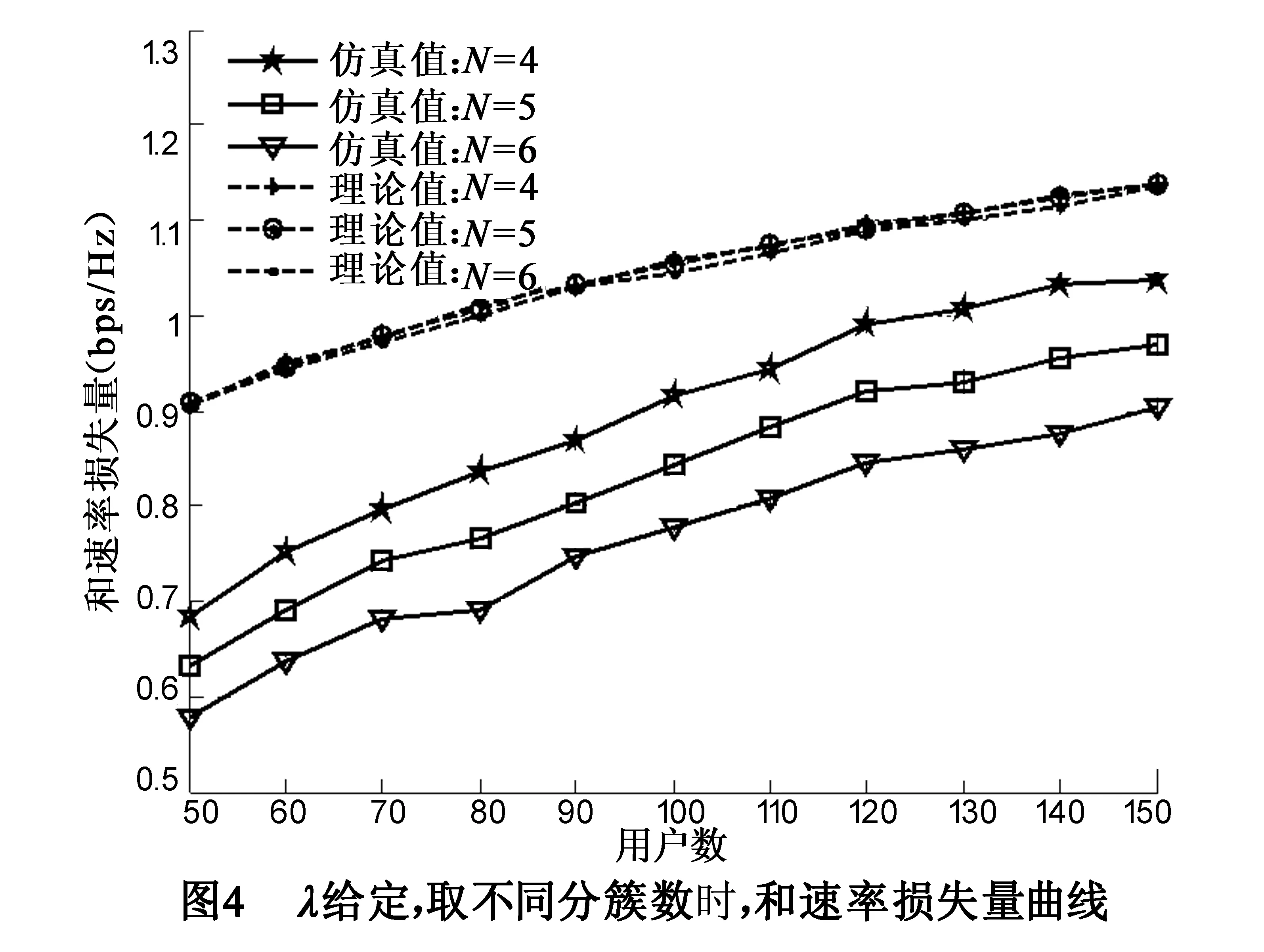
从图中曲线可以看出：

首先，随着用户数的增加，仿真值逐渐逼近于理论值，验证了关于和速率损失量理论分析的正确性.

其次，对于给定的用户数，随着分簇数增加，和速率损失量逐渐减少.原因为，从图2中可以看出，当分簇数较大时，平均反馈用户数也较多，较多的用户参与反馈降低了系统中断概率，所以造成的和速率损失量也较小.

最后，和速率损失量随着用户数K的增加而增加，再次验证了定理3的正确性.

5.3 调度公平性

由于ORBF算法要求在获得较高和速率的同时，必须要保证用户被调度的公平性，因此，本次实验从用户调度公平性方面着手，将基于分簇门限反馈的ORBF算法与经典ORBF算法进行了仿真比较.

5.4 检验多用户分集增益

针对多用户分集增益性能，本实验将基于分簇门限反馈的ORBF算法与经典ORBF算法进行了比较，仿真结果如图6所示.

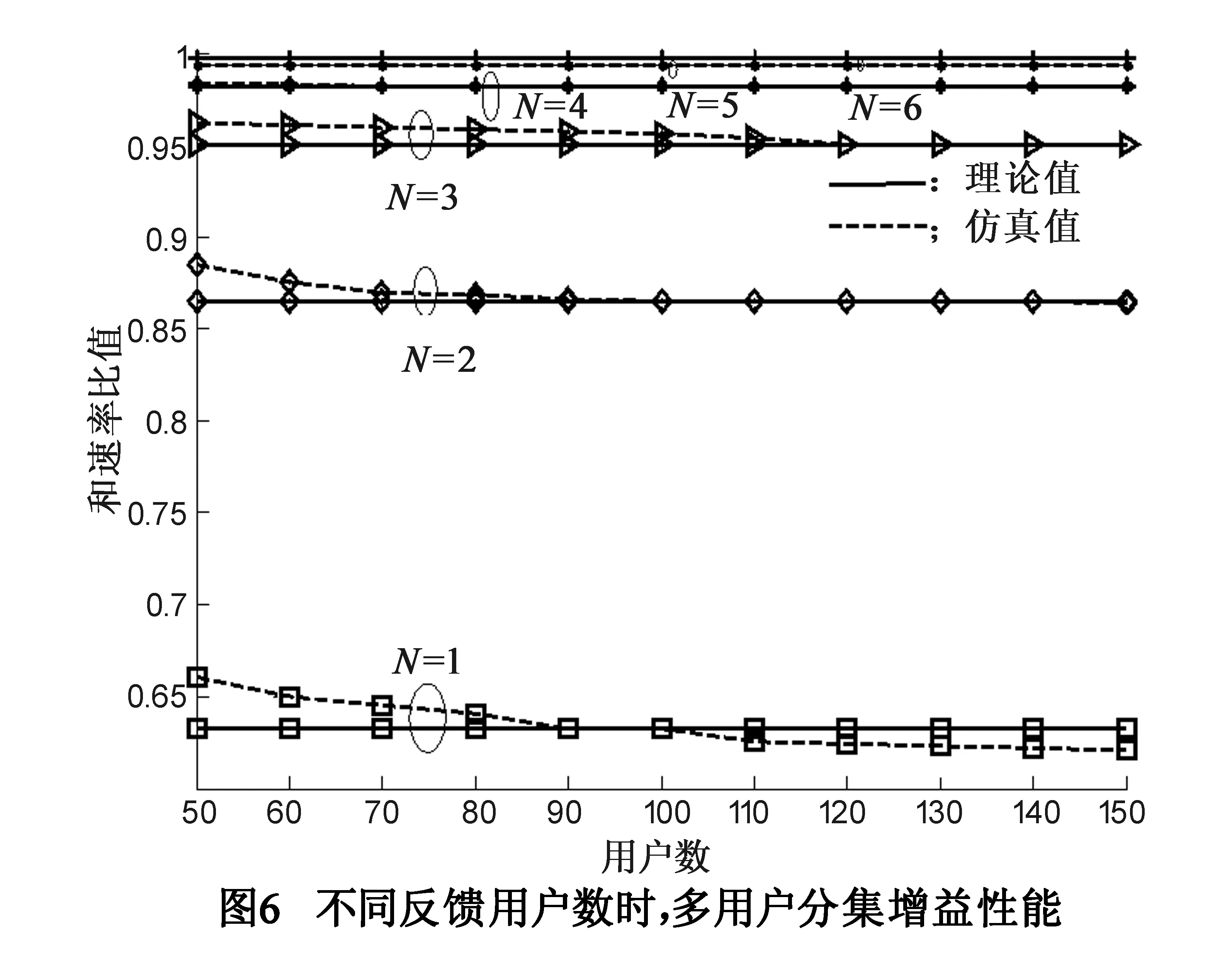
6 结束语

本文考虑存在波束间干扰的小区场景，研究满足反馈用户数约束条件时，如何有效运用ORBF算法实现和速率最大化的问题，为了降低问题直接求解的复杂度，本文采用一种基于用户信噪比信息的分簇方法，并依据极值理论，在各簇内设置反馈门限.在此基础上，本文提出了一种基于分簇门限反馈的ORBF算法.通过对算法性能的深入分析，我们使用极值理论和次序统计中的相关知识获得了该算法的和速率损失量闭合表达式以及多用户分集增益的渐进形式.仿真结果表明，新算法能够在有效控制反馈量的前提下带来几乎可忽略的和速率损失.需要指出的是，本文虽然仿真了分簇数对系统性能(和速率，公平性)的影响，发现系统性能随着分簇数的增加而得到改善.但是，系统性能是否会随着分簇数的增加而得到持续改善以及如何来确定最优的分簇数，均需要理论依据，值得进一步研究.另外，本文的讨论仅限于单小区场景，并未考虑小区间干扰，因此，在多小区场景下如何通过门限反馈策略降低反馈开销值得进一步深入探讨.

[1]Wang M,Li F,Evans J S.Opportunistic beamforming with precoder diversity in multi-user MIMO systems[A].Proceedings of IEEE Vehicular Technology Conference[C].Dresden:IEEE,2013.1-5.

[2]胡封晔,王树勋,孙晓颖,郭纲.MIMO-OFDM系统的自适应多用户分集及性能分析[J].电子学报,2008,36(7):1324-1328.

HU Feng-ye,WANG Shu-xun,SUN Xiao-ying,GUO Gang.The adaptive multi-user diversity and performance analysis based on MIMO-OFDM system[J].Acta Electronica Sinica,2008,36(7):1324-1328.(in Chinese)

[3]Weingarten H,Steinberg Y,Shamai S.The capacity region of the Gaussian multiple-input multiple-output broadcast channel[J].IEEE Transactions on Information Theory,2006,52(9):3936-3964.

[4]Yoo T,Goldsmith A.On the capacity of multiantenna broadcast scheduling using zero-forcing beamforming[J].IEEE Journal on Selected Areas in Communications,2006,24(3):528-541.

[5]Wang Q,Feng H,Cimini L J.Comparison of quantization techniques for downlink multi-user MIMO channels with limited feedback[J].IEEE Wireless Communications Letters,2014,3(2):165-168.

[6]Bayesteh A,Khandani A K.Asymptotic analysis of the amount of CSI feedback in MIMO broadcast channels[J].IEEE Transactions on Information Theory,2012,58(3):1612-1629.

[7]Sharif M,Hassibi B.On the capacity of MIMO broadcast channel with partial side information[J].IEEE Transactions on Information Theory,2005,51(2):506-522.

[8]Pugh M,Rao B D.Reduced feedback schemes using random beamforming in MIMO broadcast channels[J].IEEE Transactions on Signal Processing,2010,58(3):1821-1832.

[9]Diaz J,Simeone O,Bar-Ness Y.Asymptotic analysis of reduced-feedback strategies for MIMO Gaussian broadcast channels[J].IEEE Transactions on Information Theory,2008,54(3):1308-1316.

[10]Samarasinghe T,Inaltekin H,Evans J.The feedback-capacity tradeoff for opportunistic beamforming[A].Proceedings of IEEE International Conference on Communications[C].Kyoto:IEEE,2011.1-6.

[11]Li J H,Su H J.Feedback reduction for MIMO broadcast channel with heterogeneous fading[A].Proceedings of IEEE Symposium on Computers and Communications[C].Kerkyra:IEEE,2011.573-578.

[12]Huang Y,Rao B D.Random beamforming with heterogeneous users and selective feedback:individual sum rate and individual scaling laws[J].IEEE Transactions on Wireless Communications,2013,12(5):2080-2090.

[13]David H A,Nagaraja H N.Order Statistics[M].New York,USA:John Wiley & Sons,2003.79-126.

[14]Samarasinghe T,Inaltekin H,Evans J.Optimal selective feedback policies for opportunistic beamforming[J].IEEE Transactions on Information Theory,2013,59(5):2897-2913.

[15]Haan L,Ferreira A.Extreme Value Theory:An Introduction[M].New York,USA:Springer,2006.207-230.

[16]Bertsimas D,Natarajan K,Teo C P.Tight bounds on expected order statistics[J].Probability in the Engineering and Informational Sciences,2006,20(4):667-686.

[17]Moon S H,Lee S R,Lee I.Sum-rate capacity of random beamforming for multi-antenna broadcast channels with other cell interference[J].IEEE Transactions on Wireless Communications,2011,10(8):2440-2444.

陈兴旺 男，1988年生，安徽宿州人，中国科学技术大学硕士研究生，研究方向为MIMO预编码技术、通信信号处理.

E-mail:cxwang@mail.ustc.edu.cn

许小东 男，1976年生，安徽无为人，中国科学技术大学电子工程与信息科学系副教授，研究方向为宽带无线通信系统与信号处理.

E-mail:xdxu@ustc.edu.cn

Orthogonal Random Beamforming Based on Clustering and Feedback Threshold

CHEN Xing-wang,XU Xiao-dong

(KeyLaboratoryofWireless-OpticalCommunications,ChineseAcademyofSciences,SchoolofInformationScienceandTechnology,UniversityofScienceandTechnologyofChina,Hefei,Anhui230027,China)

This paper considers how to obtain the maximum sum-rates by using the orthogonal random beamforming (ORBF) technique under the constraint on the average number of feedback users in the context of facing inter-beam interference scenarios.Aiming to solve this problem,a novel ORBF algorithm based on clustering and feedback threshold is proposed.The users are divided into multiple clusters according to their SNRs.The corresponding feedback threshold in each cluster is calculated by the tool of extreme value theory.Finally,the new ORBF algorithm is constructed based on clustering and multiple thresholds.We make some theoretical analysis on the algorithm and derive the upper bound of sum-rates loss;the scaling law of multiuser diversity gain is also exhibited.Simulation results not only verify the validity of our analysis but also show that,when compared with the classical ORBF technique,the proposed algorithm can considerably reduce the feedback load with a good sum-rates performance.

random beamforming;inter-beam interference;clustering;feedback threshold

2014-12-26；

2015-05-15；责任编辑：孙瑶

国家863高技术发展研究计划(No.2012AA01A502)；国家自然科学基金(No.61271272)

TN929.5

A

0372-2112 (2016)08-1947-09